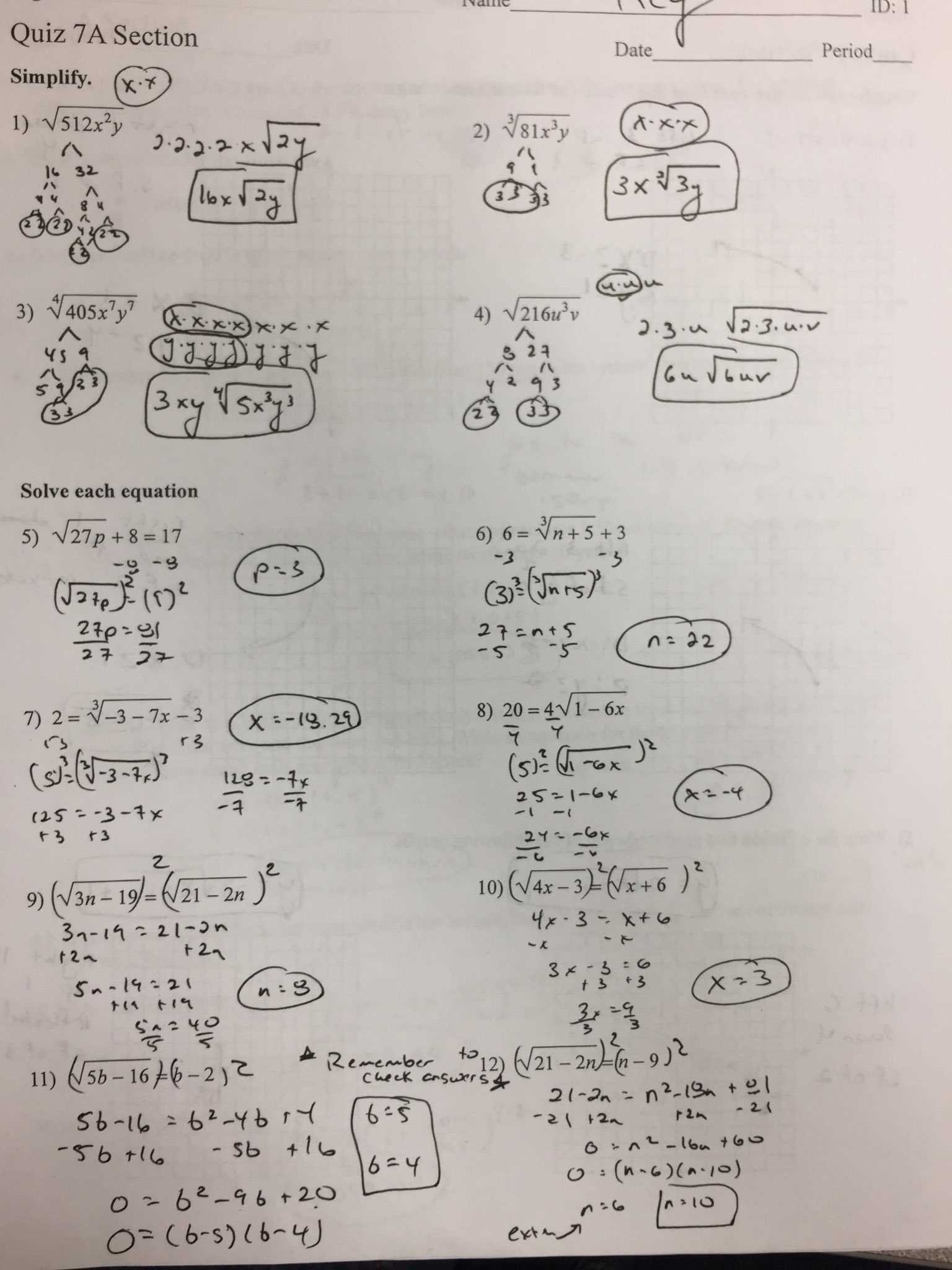
As you approach the next big assessment in your math course, it’s crucial to approach it with a clear strategy. This test will challenge your understanding of key mathematical concepts and your ability to solve problems efficiently. Whether you’re reviewing equations, functions, or graphing, a focused approach will help ensure that you feel confident and well-prepared.
Effective preparation is about more than just memorizing formulas. It involves understanding the logic behind the methods you use, practicing problem-solving techniques, and refining your test-taking skills. By organizing your study time and focusing on the most important areas, you can improve both your knowledge and your ability to tackle complex questions.
Every student has different strengths and areas for improvement, so customizing your study sessions to focus on the topics that challenge you most will maximize your chances of success. With a solid plan, you’ll be ready to perform at your best when the test day arrives.
Algebra 2 Test Preparation Guide
Success in your upcoming math assessment requires a clear and structured approach. The best way to prepare is by breaking down complex topics into manageable sections and dedicating focused time to each. This guide will walk you through key strategies to help you build confidence and improve your performance.
Key Areas to Focus On
Understanding the fundamental concepts is crucial. Here are some topics you should prioritize:
- Equations and Inequalities
- Functions and their properties
- Exponential and logarithmic expressions
- Systems of equations and graphing
- Polynomials and rational expressions
- Quadratic formulas and factoring techniques
Study Strategies for Success
Now that you know what to focus on, here are some effective methods for preparing:
- Practice regularly – Consistent practice helps reinforce concepts and improves problem-solving speed.
- Review sample problems – Work through past test questions or sample problems to understand the format and question types.
- Break it down – If you’re struggling with a specific topic, break it into smaller chunks and tackle each one individually.
- Join study groups – Discussing difficult concepts with peers can deepen your understanding and reveal different problem-solving approaches.
- Use online resources – Leverage educational websites, tutorial videos, and interactive exercises for additional practice.
Understanding the Test Format
To perform well on your upcoming assessment, it’s important to understand the structure of the test. Knowing the format allows you to better allocate your study time and approach each section with confidence. This section will guide you through the different types of questions and how they are typically organized.
| Question Type | Description |
|---|---|
| Multiple Choice | These questions will test your ability to identify the correct solution from a set of possible answers. Focus on recognizing patterns and eliminating wrong choices. |
| Short Answer | These questions require a direct, concise response. You’ll need to show your work and justify your answers clearly to receive full credit. |
| Problem Solving | These questions involve multi-step problems that test your ability to apply concepts in various scenarios. Break down each problem step by step. |
| Word Problems | These questions present real-world situations. It’s important to translate the given information into mathematical expressions and solve accordingly. |
Understanding the question types and how they are organized will help you approach the test with the right mindset. Each section requires a different set of skills, so practicing each type of question will ensure you are fully prepared.
Key Topics to Focus On
To succeed on your upcoming assessment, it’s crucial to focus on the core concepts that will appear in the test. These areas are foundational to understanding more complex problems and will give you the best chance to score highly. Below are some of the main topics you should prioritize in your study sessions.
Essential Concepts
Make sure you understand the following core concepts, as they are integral to solving a variety of problems:
- Linear and quadratic equations
- Functions and their transformations
- Systems of equations and inequalities
- Polynomials and rational expressions
- Exponential and logarithmic functions
- Complex numbers and their operations
Problem-Solving Techniques
In addition to understanding key concepts, it’s important to refine your problem-solving skills in these areas:
- Factoring methods for solving equations
- Graphing functions and interpreting their behavior
- Solving word problems involving algebraic concepts
- Manipulating and simplifying expressions
Effective Study Strategies for Success
Achieving success in your upcoming assessment requires more than just understanding the material; it also involves adopting the right study strategies. By using focused techniques, you can enhance your retention, boost problem-solving skills, and improve your confidence when facing challenging questions.
Active Learning Techniques
Instead of passively reviewing notes, engage actively with the material to deepen your understanding:
- Practice regularly: Solve a variety of problems to reinforce concepts and develop problem-solving strategies.
- Teach someone else: Explaining a topic to a peer can clarify your understanding and highlight areas where you may need more review.
- Use flashcards: Create flashcards for important formulas, concepts, and definitions to help with quick recall.
- Work through sample problems: Practice past problems or mock scenarios to simulate the test environment and assess your readiness.
Time Management and Organization
Effective preparation also depends on how you manage your time and stay organized. Here are some strategies:
- Set clear goals: Break down your study sessions into specific objectives, such as mastering a particular concept or solving a set of problems.
- Study in intervals: Use techniques like the Pomodoro method to study in focused intervals, followed by short breaks.
- Review regularly: Revisit material periodically to reinforce learning and prevent cramming.
- Stay organized: Keep your notes, assignments, and study resources neatly arranged so you can easily access them when needed.
Common Mistakes to Avoid
During your preparation for the upcoming test, it’s important to be aware of common mistakes that can hinder your progress. These errors are often made in the heat of the moment, and being mindful of them can help you avoid unnecessary setbacks. By recognizing these pitfalls, you can sharpen your approach and maximize your chances of success.
Calculation and Conceptual Errors
Many mistakes come from a misunderstanding of basic concepts or making careless calculation errors. To avoid these:
- Double-check your work: Even small mistakes in arithmetic can lead to incorrect answers. Take a moment to verify your calculations.
- Misinterpret problem instructions: Carefully read each question to understand exactly what is being asked before you begin solving.
- Forgetting negative signs: It’s easy to overlook a negative sign when solving equations. Always be cautious when dealing with negative numbers.
- Skipping steps: Rushing through multi-step problems can cause you to miss important steps. Always show your work clearly.
Poor Time Management and Stress
Another area where students commonly falter is in managing their time and stress. These issues can cloud your judgment and lead to avoidable mistakes:
- Not pacing yourself: Spending too much time on a single question can leave you with insufficient time for others. Keep track of the time and move on if you’re stuck.
- Overlooking easier questions: Don’t get bogged down in difficult problems. Complete the easier ones first to secure points, then return to the harder ones.
- Panicking under pressure: Test anxiety can cause you to make rushed decisions. Take deep breaths, stay calm, and approach each problem methodically.
Time Management Tips for Test Day
On the day of your assessment, managing your time effectively is crucial to maximizing your performance. It’s easy to get overwhelmed by the pressure of the test, but with a clear plan and focus, you can avoid common pitfalls and tackle each section efficiently. Below are some essential strategies for staying on track and making the most of your time.
Before the Test
Preparation begins long before you sit down for the test. Setting yourself up properly will help reduce stress and give you a head start:
- Get a good night’s sleep: Rest is essential for mental clarity. A well-rested mind will perform better than one that’s fatigued.
- Eat a balanced meal: Fuel your brain with healthy food that provides sustained energy, such as fruits, nuts, or whole grains.
- Arrive early: Give yourself extra time to get settled and calm your nerves. Rushing into the room can increase anxiety.
During the Test
Once the test begins, it’s all about managing your time effectively:
- Read through the entire test: Quickly skim through the questions to get a sense of what’s ahead. This will help you allocate your time wisely.
- Start with what you know: Begin by answering the questions you’re most confident in. This will help build momentum and boost your confidence.
- Keep track of time: Regularly check the clock to ensure you’re staying within your time limits. Set small goals for each section, such as completing a set number of questions in a given time frame.
- Don’t get stuck: If you encounter a challenging problem, move on and return to it later. Spending too much time on one question can prevent you from finishing the rest.
- Leave time for review: If possible, set aside a few minutes at the end to review your answers and make any necessary corrections.
Reviewing Important Mathematical Concepts
To ensure success in your upcoming test, it’s essential to review the core mathematical concepts that will form the basis of many of the questions. Understanding these key topics will not only help you solve problems more efficiently but also allow you to approach complex scenarios with confidence. Below are some of the fundamental concepts you should focus on in your preparation.
Linear Equations and Functions are fundamental in solving problems that involve straight lines. Being able to recognize the general form of an equation and interpret graphs will help you tackle many questions. Practice solving for unknowns and understand how the slope and y-intercept affect the graph’s position.
Quadratic Equations are another crucial topic. Understanding how to solve quadratic equations through factoring, completing the square, and using the quadratic formula is essential. Make sure you are comfortable with graphing parabolas and identifying key features like the vertex and axis of symmetry.
Polynomials and Rational Expressions require you to manipulate and simplify expressions. Mastery of operations with polynomials–such as addition, subtraction, multiplication, and division–is important. Additionally, be prepared to simplify rational expressions and solve equations involving rational functions.
Exponential and Logarithmic Functions are important for understanding growth and decay problems. Learn how to work with exponential equations and their inverses, logarithms. Make sure you are comfortable with the properties of logarithms and how to solve equations involving exponential and logarithmic functions.
Mastering these key concepts will provide a strong foundation for solving a wide variety of problems and enable you to approach each question with greater clarity and efficiency.
How to Solve Quadratic Equations
Quadratic equations are a fundamental part of many mathematical problems, and solving them efficiently is key to mastering various concepts. These types of equations often involve finding the values of unknown variables that satisfy the equation. Below are several common methods to solve quadratic equations that you will encounter.
Methods for Solving Quadratic Equations
There are different strategies for solving quadratic equations, and choosing the right one depends on the form of the equation you are working with:
- Factoring: This method is used when the equation can be factored easily. Start by expressing the quadratic as a product of two binomials and then set each factor equal to zero.
- Using the Quadratic Formula: The quadratic formula is a general solution to any quadratic equation of the form ax2 + bx + c = 0. The formula is:
x = (-b ± √(b² – 4ac)) / 2a
Simply plug in the values of a, b, and c from the equation and calculate the value of x.
- Completing the Square: This method involves rewriting the equation so that one side is a perfect square trinomial. Then, you can solve by taking the square root of both sides.
- Graphing: If you are familiar with graphing, you can also solve quadratic equations by finding the points where the parabola intersects the x-axis. These points represent the solutions to the equation.
Example Problems
Let’s look at a couple of examples to illustrate these methods:
- Factoring Example: Solve x2 – 5x + 6 = 0:
- Factor the quadratic: (x – 2)(x – 3) = 0
- Set each factor equal to zero: x – 2 = 0 and x – 3 = 0
- Thus, x = 2 or x = 3
- Quadratic Formula Example: Solve x2 + 4x – 5 = 0:
- Using the quadratic formula: x = (-4 ± √(4² – 4(1)(-5))) / 2(1)
- Simplifying: x = (-4 ± √(16 + 20)) / 2
- x = (-4 ± √36) / 2
- x = (-4 ± 6) / 2
- So, x = 1 or x = -5
By practicing these methods, you’ll become more comfortable solving quadratic equations and be able to tackle more complex problems with ease.
Mastering Functions and Their Graphs
Understanding functions and how to represent them visually is a crucial skill in mathematics. By learning how to manipulate functions and interpret their graphs, you can gain deeper insights into the relationships between variables and better solve a variety of problems. This section will explore the basics of functions, their properties, and how to graph them effectively.
Key Concepts of Functions
Functions are mathematical expressions that relate inputs (independent variables) to outputs (dependent variables). The graph of a function provides a visual representation of this relationship. The following are some key concepts to understand:
- Domain and Range: The domain of a function refers to all possible input values, while the range is the set of all possible output values. Identifying both is crucial when working with functions.
- Linear Functions: These are functions where the relationship between variables is represented by a straight line. They have a constant rate of change and can be written in the form y = mx + b.
- Quadratic Functions: These functions represent parabolas and are written in the form y = ax² + bx + c. They have a characteristic U-shape when graphed.
- Piecewise Functions: These functions are defined by different expressions for different intervals of the domain. Understanding how to break down these pieces is essential when graphing them.
Graphing Functions
Graphing functions involves plotting the input-output pairs on a coordinate plane. Different types of functions will have different shapes and properties on their graphs. Below are some tips for graphing:
- Identify key points: Find the x-intercepts and y-intercepts, as well as any maximum or minimum points.
- Plot points carefully: For each function, calculate several points and plot them on the graph. Then, connect the dots smoothly, considering the function’s shape.
- Consider symmetry: Some functions, like quadratic functions, have symmetrical graphs. This can help you complete the graph more efficiently.
- Check end behavior: Understand how the graph behaves as x approaches infinity or negative infinity. This will help you understand the overall shape of the graph.
Function Types and Their Graphs
Here is a brief overview of some common functions and how they appear on a graph:
| Function Type | Equation | Graph Shape |
|---|---|---|
| Linear | y = mx + b | Straight line with slope m and y-intercept b |
| Quadratic | y = ax² + bx + c | Parabola with vertex and axis of symmetry |
| Cubic | y = ax³ + bx² + cx + d | Curve with potential turning points and inflection points |
| Exponential | y = ab^x | Rapid increase or decrease, with horizontal asymptote |
Mastering the graphing of various functions will allow you to approach mathematical problems with a clear understanding of how changes in variables affect the outcome. By practicing these techniques, you will become proficient in interpreting and graphing functions with ease.
Understanding Exponential and Logarithmic Functions
Exponential and logarithmic functions are fundamental concepts in mathematics, often used to model a wide range of real-world phenomena. These functions are closely related but have distinct properties and applications. In this section, we will explore both types of functions, their behaviors, and how to solve problems involving them.
Exponential Functions
Exponential functions describe situations where a quantity grows or decays at a constant percentage rate over time. These functions are typically written in the form:
y = ab^x, where a is the initial value, b is the base (greater than 0), and x is the exponent.
The graph of an exponential function shows either rapid growth or decay, depending on the value of the base b. If b > 1, the function grows exponentially. If 0 , the function decays exponentially.
Key Properties of Exponential Functions
- Constant Rate of Change: The growth or decay occurs at a consistent rate over time.
- Asymptote: Exponential functions have a horizontal asymptote, usually at y = 0, meaning the graph approaches but never crosses this line.
- Rapid Growth/Decay: These functions can model processes such as population growth, radioactive decay, and interest accumulation.
Logarithmic Functions
Logarithmic functions are the inverse of exponential functions. A logarithmic function can be written as:
y = logb(x), where b is the base of the logarithm and x is the argument.
The logarithmic function helps to solve equations where the unknown variable is an exponent. For example, in the equation b^y = x, the logarithmic form would be y = logb(x).
Key Properties of Logarithmic Functions
- Inverse Relationship: Logarithmic functions reverse the operations of exponential functions.
- Domain: The domain of a logarithmic function is (0, ∞), meaning the argument x must be positive.
- Vertical Asymptote: Logarithmic functions have a vertical asymptote at x = 0, meaning the graph approaches this line but never crosses it.
Exponential vs. Logarithmic Functions
Although these functions are closely related, they behave differently and serve different purposes in mathematics. Exponential functions describe rapid growth or decay, while logarithmic functions are useful for solving equations where the unknown is an exponent. Understanding the interplay between these two types of functions can greatly enhance your ability to solve complex problems.
| Function Type | Equation | Graph Behavior |
|---|---|---|
| Exponential | y = ab^x | Rapid growth or decay with a horizontal asymptote |
| Logarithmic | y = logb(x) | Slow growth with a vertical asymptote at x = 0 |
By understanding the key features of both exponential and logarithmic functions, you can effectively apply them to model various scenarios and solve problems involving exponential growth, decay, and logarithmic equations.
Polynomials and Rational Expressions Explained
Polynomials and rational expressions are essential elements in mathematics, often appearing in various problems involving equations, functions, and real-world applications. Understanding their structure and behavior is key to solving complex problems and simplifying expressions. This section will break down the components of polynomials and rational expressions, explaining how they are formed and manipulated.
Understanding Polynomials
A polynomial is an algebraic expression consisting of terms with variables raised to whole number powers and multiplied by coefficients. The general form of a polynomial is:
f(x) = anxn + an-1xn-1 + … + a1x + a0, where an through a0 are constants, x is the variable, and n is the highest degree of the polynomial.
Polynomials can have different degrees, with the highest degree determining the overall shape and behavior of the function. The degree of a polynomial is the exponent of the term with the highest power of x.
Key Characteristics of Polynomials
- Degree: The highest power of x in the polynomial.
- Terms: Polynomials consist of one or more terms, which are individual components of the expression.
- Coefficients: The constants multiplying the variable terms.
- End Behavior: The behavior of the graph of a polynomial as x approaches positive or negative infinity.
Rational Expressions
Rational expressions are fractions where both the numerator and the denominator are polynomials. They can be simplified, added, subtracted, multiplied, and divided just like numerical fractions. The general form of a rational expression is:
R(x) = (p(x)) / (q(x)), where p(x) and q(x) are polynomials and q(x) ≠ 0.
Operations with Rational Expressions
Just like regular fractions, rational expressions can undergo operations such as:
- Simplification: Dividing both the numerator and denominator by their greatest common factor.
- Addition and Subtraction: To add or subtract, find a common denominator.
- Multiplication and Division: Multiply the numerators and denominators, and simplify the result.
Key Concepts for Simplifying Rational Expressions
- Factorization: Factoring polynomials in the numerator and denominator to simplify the expression.
- Domain: The domain of a rational expression includes all real numbers except those that make the denominator equal to zero.
- Restrictions: Identify values that cause division by zero and exclude them from the domain.
Mastering polynomials and rational expressions is crucial for tackling a wide range of mathematical problems, from graphing functions to solving complex equations. By understanding the structure, operations, and simplification techniques, you can efficiently work with these expressions in various contexts.
Tips for Word Problems in Algebra
Word problems can often feel overwhelming, especially when translating real-world scenarios into mathematical expressions. However, with a strategic approach, these types of problems can become more manageable. The key to solving word problems lies in understanding the question, identifying the relevant information, and translating that information into equations or expressions.
Steps to Tackle Word Problems
Follow these steps to make word problems more approachable:
- Read the Problem Carefully: Ensure you understand the entire scenario before proceeding. Identify the unknowns and what is being asked.
- Identify Key Information: Look for numbers, units, and relationships in the problem. Highlight or underline these details to keep track of them.
- Define Variables: Assign variables to the unknowns in the problem. For example, let x represent the number of items, time, or any other unknown quantity.
- Translate into an Equation: Use the information to form a mathematical expression or equation that models the situation described.
- Solve the Equation: Apply appropriate algebraic methods to solve for the unknown variable(s).
- Check Your Solution: Plug the answer back into the context of the problem to make sure it makes sense and satisfies all conditions.
Common Strategies for Word Problems
Different types of word problems may require specific approaches. Here are some helpful strategies:
- Unit Conversion: If the problem involves different units (e.g., inches to feet), be sure to convert them to a consistent unit before solving.
- Work with Ratios: Many word problems involve ratios or proportions. Set up the relationship between quantities and solve accordingly.
- Break Down Complex Problems: For multi-step problems, break them down into smaller, more manageable parts. Solve each part step by step.
- Use Diagrams: Visualizing the problem with a diagram, chart, or table can help clarify the relationships between quantities.
- Use Logical Reasoning: Sometimes a logical approach can guide you to the correct equation or solution, especially when interpreting words like “more than,” “less than,” “total,” etc.
Practice Makes Perfect
As with any mathematical skill, practice is essential for mastering word problems. Regularly working through problems will help improve your problem-solving abilities and make you more confident in approaching different scenarios. The more you practice, the easier it becomes to spot the patterns and strategies needed to solve a wide range of problems.
Utilizing Practice Exams Effectively
Practice tests are an essential tool for preparing for any type of assessment. By simulating the conditions of the actual evaluation, they help you familiarize yourself with the format, identify areas that need improvement, and build confidence. The key to making the most out of practice tests lies in how you approach them–whether you use them to identify knowledge gaps or to practice time management techniques.
Maximizing the Benefits of Practice Tests
Here are some strategies to get the most out of your practice sessions:
- Simulate Real Conditions: Take the practice test under timed conditions, just as you would during the actual evaluation. This helps you become comfortable with pacing and ensures you’re prepared for the pressure of completing the test on time.
- Review Mistakes Thoroughly: After completing a practice test, focus on reviewing each mistake carefully. Understand why you made the error and go over the concepts that need more attention. This will help you reinforce your learning.
- Track Your Progress: Keep a record of your scores across multiple practice sessions. Tracking improvements and areas of difficulty will allow you to see where you need more practice and ensure that you’re progressing towards mastering the material.
- Focus on Weak Areas: If certain topics or types of questions are consistently challenging, dedicate more time to studying those areas. Use practice tests as a tool to target your weaknesses, rather than just a way to review what you already know.
Creating a Practice Test Routine
To maximize the effectiveness of practice tests, establish a regular routine leading up to your assessment:
- Start Early: Begin taking practice tests early in your preparation process. This allows you to gradually build up your skills and reduce stress as the test date approaches.
- Take Breaks Between Sessions: Avoid taking too many practice tests in one sitting. Give yourself time to rest and process the material in between sessions, so that you’re not overwhelmed or fatigued.
- Gradually Increase Difficulty: As you get more comfortable with the material, increase the difficulty of your practice tests. Try including a variety of question types and more challenging problems to stretch your abilities.
By consistently incorporating practice tests into your preparation routine, you’ll not only improve your understanding of the material but also become more familiar with the format, enhancing your performance during the actual assessment.
Staying Calm During the Test
During any important assessment, it is common to experience stress or anxiety, which can negatively affect your performance. The key to success lies in staying calm and composed throughout the process. Managing your emotions effectively allows you to think clearly, approach problems with confidence, and avoid making careless mistakes. There are several strategies you can use to keep yourself calm and focused while working through the test.
- Take Deep Breaths: When you begin to feel overwhelmed, pause for a moment and take deep, slow breaths. This helps to reduce anxiety, lower your heart rate, and clear your mind, making it easier to concentrate on the task at hand.
- Stay Positive: Cultivate a positive mindset by focusing on your strengths. Remind yourself of the preparation you’ve done and your ability to handle the challenges. Confidence can help minimize nervousness and increase your overall performance.
- Break the Test Into Sections: Rather than thinking of the test as one large challenge, break it down into smaller, more manageable parts. Tackling one section at a time makes the whole process feel less daunting and keeps you from becoming overwhelmed.
- Focus on What You Know: Start with the questions you feel most confident about. This will build your momentum and help you approach more difficult questions with a sense of accomplishment and self-assurance.
- Manage Your Time Wisely: Keep track of time without obsessing over it. If you encounter a question that is taking too long, move on and come back to it later. Ensuring you have time for all sections will reduce stress and prevent rushing through the later parts of the assessment.
By applying these techniques, you can maintain a sense of calm throughout the assessment, allowing you to perform at your best under pressure. A calm mindset helps you think more clearly, make better decisions, and approach each problem with a positive and focused attitude.
Test-Taking Strategies for Algebra 2
Approaching a challenging assessment requires more than just understanding the material. It involves effective strategies to manage your time, ensure accuracy, and minimize mistakes under pressure. Whether you’re dealing with complex equations or intricate concepts, having a clear plan of action can make a significant difference in how you perform. By using the right strategies, you can tackle questions efficiently and boost your confidence throughout the process.
Time Management
Efficiently managing your time is crucial during any assessment. Without proper time allocation, it’s easy to rush through questions or leave some unanswered. Here’s a helpful approach:
| Strategy | Benefits |
|---|---|
| Start with the easier questions | Helps build confidence and ensures you get points for known material |
| Move on if stuck | Prevents wasting too much time on one question |
| Leave time for review | Allows you to check answers and correct errors before submitting |
Effective Problem-Solving Techniques
To approach each problem methodically, break it down into smaller steps. This will help you to focus on one aspect of the problem at a time and avoid feeling overwhelmed. Follow these simple steps:
- Read the problem carefully: Understand exactly what is being asked before attempting a solution.
- Write down known information: Organize the data or equations you have, making it easier to identify the next steps.
- Look for patterns: Many problems have recognizable patterns or shortcuts that can save you time.
- Check your work: Always review your calculations and solutions before finalizing your answer.
By following these strategies, you can manage your time better, minimize errors, and approach each problem with a clear and focused mindset. The right techniques can make even the most challenging tasks more manageable, leading to a more successful performance.
How to Handle Complex Numbers
When dealing with advanced mathematical concepts, complex numbers can seem intimidating at first. However, with the right approach, understanding and solving problems involving these numbers becomes much easier. Complex numbers consist of a real part and an imaginary part, and they often appear in situations where regular numbers do not provide solutions, such as in the case of negative square roots. Mastering how to handle these numbers is essential for solving a wide range of problems in higher-level mathematics.
One of the first things to grasp is the concept of the imaginary unit, denoted as i, where i represents the square root of -1. Once you understand this basic principle, the rest falls into place, as you can now express complex numbers as a combination of real and imaginary parts. For example, a complex number might look like 3 + 4i, where 3 is the real part and 4i is the imaginary part.
To work with these numbers, you’ll need to learn how to perform basic arithmetic operations like addition, subtraction, multiplication, and division. Here are some key points to remember:
- Addition/Subtraction: Add or subtract the real parts and the imaginary parts separately. For example, (3 + 4i) + (2 – 3i) = 5 + i.
- Multiplication: Use the distributive property, keeping in mind that i^2 = -1. For example, (3 + 4i) * (1 – 2i) = 11 – 2i.
- Division: To divide complex numbers, multiply the numerator and denominator by the conjugate of the denominator. The conjugate of a complex number is obtained by changing the sign of its imaginary part. For example, (3 + 4i) ÷ (1 – 2i) would require multiplying both the numerator and denominator by (1 + 2i).
Understanding complex numbers is vital not only for solving specific problems but also for grasping higher-level concepts that you may encounter in advanced mathematics. The key is to practice these operations until they become second nature, making complex numbers easier to handle in various contexts.
Preparing for Algebra 2 Beyond Midterms
Once you’ve navigated the initial assessments and challenges, it’s important to think about the long-term success in your mathematical journey. The key to mastering advanced topics in mathematics lies not just in preparing for individual evaluations, but in developing a deeper understanding of the concepts that will carry you through more complex problems. As you move beyond tests, focusing on reinforcing foundational skills while staying engaged with new material is essential for continued progress.
One of the most effective strategies is to build on the concepts you’ve already learned and expand your knowledge gradually. This approach allows you to keep your skills sharp and helps you build confidence when approaching new topics. Don’t just review material before a test; incorporate it into your daily practice and real-life applications. Working on problems that challenge you outside of class can deepen your understanding and improve your problem-solving abilities.
Strengthening Core Concepts
Mastering the fundamentals of advanced mathematics is essential for success in future studies. Whether it’s complex numbers, functions, or polynomials, solidifying your core knowledge is vital for progressing to more difficult topics. Try to:
- Review key operations: Regularly practice operations involving real and imaginary numbers, polynomials, and rational expressions.
- Understand graphs: Strengthen your ability to interpret and graph different functions, as visualizing equations often makes them easier to manipulate.
- Work with word problems: Challenge yourself by applying concepts to real-world scenarios that require more critical thinking and problem-solving skills.
Engaging with Advanced Topics
As you continue your mathematical journey, it’s helpful to start previewing topics that will appear later in your coursework. Engaging with advanced topics early can provide an edge when you encounter them in more depth. Here are some strategies for advancing beyond your current level:
- Explore new theories: Read about higher-level concepts like matrices, systems of equations, and calculus to build a strong foundation for future studies.
- Use online resources: Leverage tutorials, videos, and forums that break down complex concepts in a way that complements your classroom learning.
- Seek additional practice: Make use of extra exercises or problems that challenge your understanding and allow you to apply the knowledge you’ve gained in novel ways.
By focusing on mastering both current and future material, you’ll not only excel in the present but also set yourself up for continued success in mathematics. Keep practicing, stay curious, and approach every new challenge with the same dedication and enthusiasm.