
As students prepare for advanced mathematical assessments, understanding complex concepts and mastering problem-solving techniques becomes crucial. This section focuses on providing clear, step-by-step solutions to the most challenging areas of the curriculum. By breaking down each problem, students can gain confidence and improve their problem-solving skills, ensuring a strong performance on their exams.
Focusing on essential skills such as equation solving, graph analysis, and function manipulation, this guide will help learners approach each question with a methodical mindset. Whether tackling polynomial expressions, analyzing geometric patterns, or interpreting data, this resource offers valuable insights for mastering these critical topics.
With targeted practice and strategic study techniques, students will be better equipped to navigate the test efficiently. This article highlights the importance of knowing which strategies work best for specific question types, ensuring success in each aspect of the assessment.
Mathematical Exam Overview
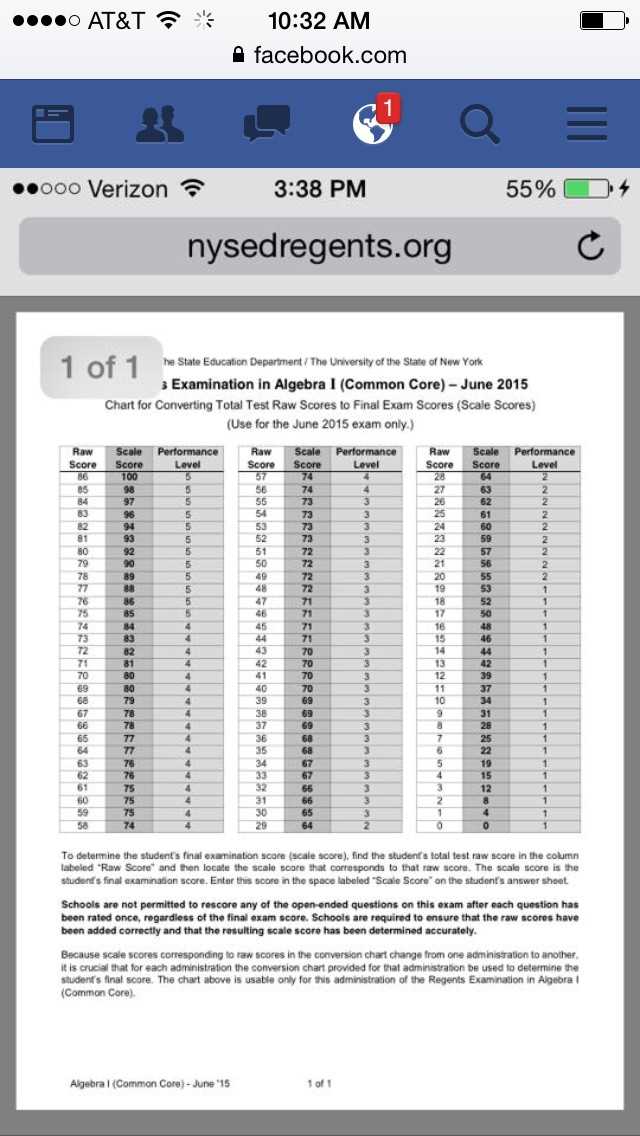
The exam is designed to assess students’ proficiency in key areas of advanced mathematics. It tests a variety of topics, requiring a comprehensive understanding of concepts, problem-solving abilities, and analytical skills. The test format includes a combination of multiple-choice and constructed-response questions, each targeting different aspects of mathematical knowledge.
In this section, we will explore the structure of the exam, focusing on the critical components that students should master in order to perform well. By identifying the core areas of focus, learners can better organize their study time and approach the test with confidence.
Core Topics Covered
The exam evaluates a wide range of mathematical principles, including functions, equations, and graph interpretation. Students must be able to demonstrate their understanding of both theoretical concepts and their practical application in solving problems. Some of the main topics include solving equations, analyzing geometric figures, and working with statistical data.
Test Structure and Tips

Understanding the layout of the exam is essential for time management. The test is divided into sections, each addressing different types of questions. The key to success is familiarity with the question types and practicing under timed conditions to build efficiency and accuracy.
Understanding Key Topics for Success
To excel in the exam, it is crucial to grasp the foundational concepts that are tested. Focusing on these key topics not only helps with exam preparation but also enhances the ability to solve complex problems under time pressure. By mastering these areas, students can improve both their accuracy and speed when tackling different question types.
Here are some of the most important topics to focus on for success:
| Topic | Description |
|---|---|
| Equations and Inequalities | Understanding how to manipulate and solve various types of equations, including linear, quadratic, and rational equations. |
| Functions and Graphs | Ability to interpret and analyze functions, as well as graph them accurately to identify key features such as intercepts and asymptotes. |
| Polynomials and Factoring | Knowledge of how to factor polynomials, simplify expressions, and solve problems involving quadratic and higher-degree polynomials. |
| Systems of Equations | Mastering methods to solve systems of linear and nonlinear equations, including substitution and elimination techniques. |
| Trigonometric Functions | Understanding the properties and graphs of trigonometric functions, as well as solving equations involving these functions. |
| Statistics and Probability | Ability to interpret statistical data, calculate probabilities, and understand measures of central tendency and dispersion. |
Focusing on these topics ensures a well-rounded preparation strategy, helping students tackle the most common question types effectively. Each topic requires both theoretical understanding and practical problem-solving skills, so consistent practice is key to mastering them.
Important Formulas to Remember
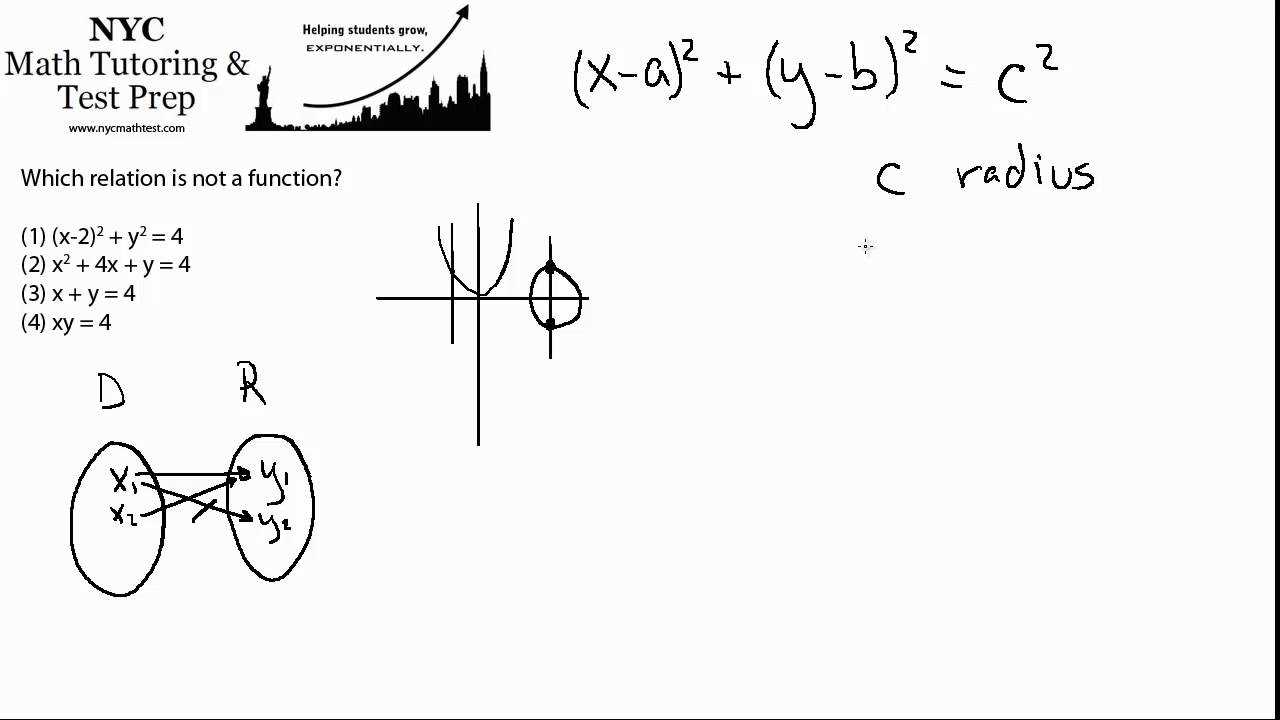
Memorizing essential formulas is a key step in preparing for the exam. These formulas serve as the foundation for solving problems across various topics, from equations to graph analysis. Having a solid grasp of these formulas allows you to quickly apply them to different question types, saving valuable time during the test.
Basic Mathematical Formulas
The following formulas are fundamental to many areas of the exam. Make sure to understand their applications and practice using them:
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a
- Slope of a Line: m = (y₂ – y₁) / (x₂ – x₁)
- Pythagorean Theorem: a² + b² = c²
- Area of a Triangle: A = 1/2 * base * height
- Circumference of a Circle: C = 2πr
- Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²)
Advanced Formulas
For more advanced problems, these formulas are crucial for solving complex equations and understanding graphs:
- Exponential Growth/Decay: A = P(1 + r/n)^(nt)
- Logarithmic Formula: logₐ(x) = y if aᵧ = x
- Sum of an Arithmetic Sequence: Sₙ = n/2 * (a₁ + aₙ)
- Sum of a Geometric Series: Sₙ = a₁ * (1 – rⁿ) / (1 – r)
Remember, the key to mastering these formulas is consistent practice. As you familiarize yourself with their use, you’ll become more efficient in applying them under test conditions.
How to Solve Trigonometric Equations
Solving equations involving periodic functions requires a strong understanding of both the properties of the functions and the techniques for isolating the unknown. These types of problems often involve manipulating expressions and finding all possible solutions within a specific range. The goal is to find values that satisfy the equation, considering the periodic nature of the functions involved.
To solve these equations effectively, follow these general steps:
- Step 1: Identify the function type, such as sine, cosine, or tangent, and determine the range of possible solutions.
- Step 2: Isolate the trigonometric function on one side of the equation. This may involve algebraic manipulation such as factoring or applying identities.
- Step 3: Solve for the angle, using inverse functions or other methods depending on the type of equation.
- Step 4: Consider all possible solutions, taking into account the periodicity of the function. Multiple solutions may exist depending on the interval.
- Step 5: Check the solutions by substituting them back into the original equation to ensure they are correct.
For example, to solve an equation like sin(x) = 0.5, first find the principal angle, then determine other possible angles within the given range, as sine is periodic.
Mastering these steps and practicing regularly with different equations will build proficiency and help you approach more complex problems with confidence.
Tips for Tackling Word Problems

Word problems can seem intimidating, but with the right approach, they become manageable challenges. The key is to carefully analyze the information given and translate it into mathematical expressions that can be solved step by step. By following a systematic strategy, you can break down complex scenarios into simpler tasks.
Here are some helpful tips for approaching word problems:
- Read the problem carefully: Make sure you understand all the details before trying to solve it. Pay attention to what is being asked and highlight or underline important information.
- Identify the variables: Define the unknowns in the problem. Assign variables to the quantities you’re solving for, and write them clearly in your working.
- Translate words into equations: Convert the verbal descriptions into mathematical expressions. Look for key phrases like “sum,” “difference,” or “product” to guide you.
- Organize your work: Break the problem down into smaller, manageable steps. Write out each step clearly, showing how you arrived at your solution.
- Check your units: Ensure that the units of measurement are consistent throughout the problem. If necessary, convert units before performing calculations.
- Review the solution: After solving, revisit the problem to verify that your answer makes sense in the context of the question. Double-check your work for any errors or misinterpretations.
By following these steps, you can build confidence in solving word problems and improve your overall problem-solving skills.
Common Mistakes to Avoid

When solving mathematical problems, it’s easy to overlook small details that can lead to incorrect solutions. By being aware of common pitfalls, you can avoid costly mistakes and improve your accuracy. Understanding where errors are likely to occur helps you stay focused and ensures that you apply the right methods at each step.
Calculation Errors
One of the most frequent mistakes in problem-solving is simple arithmetic errors. These mistakes can happen when performing basic operations like addition, subtraction, multiplication, or division. Always double-check your calculations, especially when working with larger numbers or more complex expressions. Using a calculator or performing operations step by step can help reduce this type of error.
Misinterpreting the Problem
Another common mistake is misunderstanding the question or misreading key information. It’s essential to clearly identify what is being asked and the values provided. Make sure to translate word problems accurately into mathematical terms, and pay close attention to units or specific instructions in the question. Skipping these steps can lead to incorrect assumptions and the wrong approach to solving the problem.
By recognizing these common mistakes and taking extra care during the problem-solving process, you can improve both the accuracy and efficiency of your work.
Test Strategies for Time Management
Effective time management during an exam is crucial for maximizing performance and ensuring that all questions are answered. A well-structured approach allows you to allocate sufficient time to each section, reduces stress, and prevents you from rushing through the most difficult questions. By using smart strategies, you can complete the test efficiently without sacrificing accuracy.
Here are some time management strategies to consider during your exam:
- Familiarize Yourself with the Test Format: Before the exam, review the structure and types of questions. Knowing how much time to allocate to each section helps you plan your strategy.
- Set a Time Limit for Each Question: Divide the total available time by the number of questions to establish a time limit for each one. This keeps you from spending too long on any individual question.
- Answer the Easy Questions First: Quickly go through the test and answer the questions you find easiest. This will build confidence and leave more time for challenging problems.
- Mark Difficult Questions and Move On: If you encounter a difficult question, don’t get stuck. Mark it and move on to the next. Come back to it after you’ve completed the rest of the exam.
- Leave Time for Review: Always save the last 5-10 minutes to review your answers. This allows you to catch any mistakes or revisit unanswered questions.
- Practice Time Management in Simulated Tests: Prior to the exam, practice under timed conditions. This will help you get comfortable with the pace required and refine your strategy.
By implementing these time management techniques, you can ensure that you remain calm and collected throughout the exam, giving yourself the best chance for success.
How to Interpret Graphs Effectively
Interpreting graphs is an essential skill for solving problems that involve visual representations of data or equations. Graphs can provide valuable insights into trends, relationships, and key features of a mathematical function. By understanding how to read and analyze graphs, you can extract useful information and make accurate decisions based on the visual data presented.
Here are some strategies for interpreting graphs effectively:
- Understand the Axes: Before analyzing the graph, carefully examine the axes. Ensure you understand the scale, the units of measurement, and what each axis represents. This will give context to the data shown.
- Identify Key Points: Focus on critical points such as intercepts, peaks, and valleys. These points can give you important information about the behavior of the graph, such as where a function crosses the axis or reaches its maximum or minimum values.
- Look for Patterns: Observe any consistent trends, whether increasing or decreasing. Identifying patterns will help you predict the behavior of the graph over a broader range.
- Examine the Shape of the Graph: Different shapes indicate different types of functions. For example, a straight line suggests a linear relationship, while a curve may indicate exponential or quadratic behavior. Understanding the shape can help you infer the underlying function.
- Consider the Domain and Range: Pay attention to the range of values on the axes and the points that the graph covers. The domain refers to the set of possible input values, while the range refers to the output values represented on the graph.
- Analyze Asymptotes and Discontinuities: Check for any asymptotes (lines that the graph approaches but never touches) or discontinuities (gaps in the graph). These features are often critical in understanding the behavior of the function over different intervals.
By using these techniques, you can improve your ability to extract meaningful information from graphs and use that understanding to solve problems more effectively.
Study Resources for Algebra 2 Trig
Having the right study materials is crucial when preparing for a mathematical exam. There are many resources available to help you understand the core concepts and improve your problem-solving skills. Whether you’re looking for practice problems, detailed explanations, or interactive tools, choosing the right materials can make a significant difference in your performance.
Here are some valuable study resources to help you succeed:
- Textbooks and Course Materials: Start with your class materials, as they often provide a structured and thorough approach to the subject. Textbooks typically include examples, practice questions, and step-by-step solutions that help you understand key concepts.
- Online Tutorials: Websites like Khan Academy and Coursera offer video lessons on a wide range of topics. These tutorials often explain concepts from multiple angles, making them a great tool for reinforcement.
- Practice Worksheets: Many educational websites provide downloadable worksheets with problems to practice. Working through these worksheets will help reinforce what you’ve learned and improve your confidence.
- Interactive Apps: Apps like Wolfram Alpha and Desmos allow you to graph equations and visualize mathematical relationships. These tools can help you better understand abstract concepts by giving you hands-on experience.
- Study Groups: Collaborating with peers can enhance your understanding of difficult topics. Discussing problems and solutions in a group setting often provides different perspectives and helps reinforce learning.
- Flashcards: Create or find online flashcards to help you memorize important formulas, definitions, and methods. Flashcards are particularly useful for quick review sessions and to test your recall under time constraints.
- Private Tutors: If you need personalized help, consider working with a tutor. Tutors can provide one-on-one explanations and address your specific areas of difficulty, ensuring targeted learning.
Using a combination of these resources will not only prepare you for exams but also deepen your understanding of mathematical principles, giving you the tools you need for future success.
Practice Problems and Solutions

Regular practice is essential for mastering mathematical concepts. Solving problems helps reinforce your understanding and improves problem-solving speed. By working through a variety of questions, you can familiarize yourself with different problem types and develop strategies for tackling more complex scenarios. Below are some practice problems followed by step-by-step solutions to guide you through the process.
Practice Problems
- Problem 1: Solve the equation: 3x + 5 = 20.
- Problem 2: Simplify the expression: (2x + 4)(x – 3).
- Problem 3: Find the roots of the quadratic equation: x² – 5x + 6 = 0.
- Problem 4: Graph the linear equation: y = 2x + 3.
- Problem 5: Evaluate the function: f(x) = x² + 4x – 7 when x = -2.
Solutions
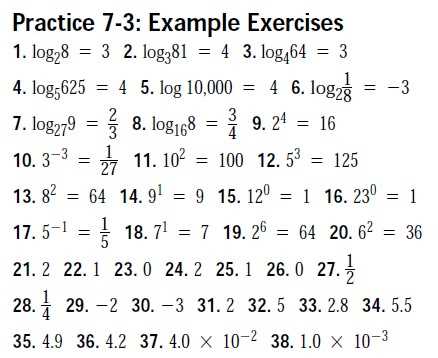
- Solution 1: To solve 3x + 5 = 20:
- Subtract 5 from both sides: 3x = 15.
- Divide both sides by 3: x = 5.
- Solution 2: To simplify (2x + 4)(x – 3):
- Apply the distributive property: 2x(x – 3) + 4(x – 3).
- Multiply each term: 2x² – 6x + 4x – 12.
- Combine like terms: 2x² – 2x – 12.
- Solution 3: To find the roots of x² – 5x + 6 = 0:
- Factor the quadratic equation: (x – 2)(x – 3) = 0.
- Set each factor equal to zero: x – 2 = 0 or x – 3 = 0.
- Solve for x: x = 2 or x = 3.
- Solution 4: To graph y = 2x + 3:
- Plot the y-intercept at (0, 3).
- Use the slope of 2 (rise over run) to plot another point: (1, 5).
- Basic Arithmetic Functions: Ensure that you are comfortable with performing simple calculations such as addition, subtraction, multiplication, and division quickly.
- Memory Functions: Use the memory keys (M+, M-, MR, and MC) to store intermediate results, which can help you avoid repeating steps in long calculations.
- Parentheses: Master the use of parentheses to structure your calculations and ensure that operations are carried out in the correct order.
- Square Roots and Powers: Know how to use the square root function and raise numbers to a power for solving equations that require exponents or roots.
- Scientific Functions: Familiarize yourself with advanced functions like sine, cosine, and tangent for trigonometric problems, as well as logarithms and exponents for more complex calculations.
- Use Parentheses Wisely: When entering long expressions, group parts of the equation with parentheses to ensure that operations are executed in the correct order. This is especially important in formulas with multiple steps.
- Break Down Complex Problems: If a problem has multiple steps, break it down into smaller parts and store intermediate results in memory. This prevents errors and makes the solution process smoother.
- Check for Mistakes: Always double-check your input before pressing the equals button. It’s easy to make small mistakes when typing in numbers or operators, which can affect your final result.
- Use the Calculator’s Features for Efficiency: Many calculators offer a multi-line display or history feature. Use these to review previous calculations and avoid redoing work unnecessarily.
- Practice Regularly: The more familiar you are with your calculator’s functions, the faster you’ll be able to solve problems under time pressure. Practice solving a variety of problems using your calculator to become more proficient.
- Multiple Choice: These questions provide several options, and you must choose the correct one. They test your ability to recognize correct solutions quickly.
- Short Answer: These questions require you to solve problems and write out the solution. They are designed to assess your understanding of key concepts and your ability to apply them.
- Extended Response: These questions require more detailed solutions, often involving several steps. You will need to clearly show your work and explain your reasoning.
How to Use a Calculator Efficiently
Understanding how to use a calculator effectively can save time and help you solve complex problems more accurately. Many exams and assignments allow the use of a calculator, and knowing how to maximize its features can make a significant difference in your performance. Below are some tips to help you get the most out of your calculator during your studies.
Key Features to Master
Efficient Techniques for Solving Problems
By mastering these techniques and learning to utilize your calculator’s features effectively, you can reduce errors and save time during problem-solving, helping you perform better in tests and assignments.
Understanding the Exam Format
Familiarizing yourself with the structure and layout of an exam is essential for maximizing your performance. Knowing what to expect can reduce anxiety and help you allocate your time efficiently during the test. This section will provide an overview of the key components of the exam and how to navigate each section successfully.
Exam Structure Overview
The test is typically divided into multiple sections, each focusing on different aspects of the material. These sections may include a mix of multiple-choice questions, short-answer problems, and extended response tasks that require you to show your work and reasoning. Understanding the weight of each section can help you prioritize your time accordingly.
Types of Questions
By becoming familiar with the exam format, you can approach each section with confidence and manage your time more effectively throughout the test.
Key Concepts in Trigonometry
Understanding fundamental principles is crucial for solving complex mathematical problems. In this section, we will explore some of the most important ideas that form the basis of solving problems related to angles and their relationships in various contexts. Mastering these concepts will help you tackle a wide range of questions and improve your problem-solving skills.
Angles and their Measurements: The study of angles is central to many mathematical applications. Angles can be measured in both degrees and radians. Knowing how to convert between these two units and how to apply them in different scenarios is essential for solving many problems.
Functions of Angles: Functions such as sine, cosine, and tangent are used to relate the angles of a right triangle to the ratios of its sides. These relationships are key in solving problems involving right triangles and periodic phenomena.
Unit Circle: The unit circle is a powerful tool used to understand the relationships between angles and their corresponding trigonometric values. It helps you visualize and calculate the sine, cosine, and tangent of different angles and is crucial for understanding the behavior of these functions on a graph.
Graphing Trigonometric Functions: The ability to graph functions like sine, cosine, and tangent is an important skill. These graphs help to visualize the periodic nature of these functions and understand their behavior over different intervals.
Solving Equations: Trigonometric equations often involve finding unknown angles based on given values of the trigonometric functions. Being able to solve these equations requires understanding the identities and properties of the functions, as well as using inverse functions to determine angle measures.
By mastering these key concepts, you will be able to approach problems with confidence and apply your knowledge to a variety of mathematical challenges.
Breaking Down Complex Functions
Complex functions can often appear intimidating at first glance, but with the right approach, they can be understood and simplified. In this section, we will examine methods for breaking down intricate expressions into more manageable parts. By recognizing patterns and applying foundational rules, you can solve even the most complicated problems with confidence.
Identifying Key Components
The first step in simplifying complex functions is to identify the key components that make up the expression. These might include constants, variables, and various operations that are being performed. Once you understand the structure, you can focus on simplifying each part individually before combining them for the final solution.
Using Identities and Properties
Mathematical identities and properties often play a crucial role in breaking down complex expressions. By applying known rules, such as distributive or associative properties, you can simplify complex functions step-by-step. Below is a table of commonly used identities that can help simplify certain types of functions:
Identity Description Distributive Property a(b + c) = ab + ac Pythagorean Identity sin²(x) + cos²(x) = 1 Power Rule d/dx [x^n] = nx^(n-1) Sum of Angles sin(a + b) = sin(a)cos(b) + cos(a)sin(b) By systematically applying these identities, you can simplify complex functions and make problem-solving more manageable. Understanding the underlying structure is key to successfully breaking down intricate expressions.
Reviewing Algebraic Manipulation Skills
Mastering the art of manipulating mathematical expressions is essential for solving a wide range of problems. In this section, we will focus on reinforcing core skills that allow you to simplify, factor, and rearrange equations effectively. These techniques are foundational and provide the necessary tools for tackling more advanced concepts and problems.
One of the first skills to review is simplifying expressions by combining like terms. This process involves identifying terms that share the same variables or powers and then adding or subtracting them accordingly. Next, it’s important to become comfortable with factoring polynomials, a key method for solving quadratic equations and higher-degree functions. Understanding how to factor expressions into their simplest form is crucial for progressing in more complex problem-solving tasks.
Another essential technique involves solving equations by isolating variables. Whether you’re dealing with linear, quadratic, or rational equations, being able to manipulate the equation to isolate the unknowns is fundamental. This includes using operations such as addition, subtraction, multiplication, division, and applying inverse operations to simplify the equation step by step.
Through practice and consistent application of these skills, you will build the confidence needed to approach a variety of mathematical challenges with ease. Developing strong algebraic manipulation skills is key to progressing in your studies and achieving success in more advanced topics.
How to Approach Multiple Choice Questions

Multiple choice questions can be both a challenge and an opportunity to demonstrate your understanding of various concepts. The key to success with this question type lies in strategy and preparation. By applying focused techniques, you can navigate through the options and identify the correct answer more efficiently.
When facing a multiple choice question, the first step is to read the question carefully and understand what is being asked. Often, there will be subtle clues within the phrasing that can direct you toward the right approach. Once the question is clear, eliminate the obviously incorrect answers. This process of elimination can significantly improve your odds of selecting the correct answer, especially when you’re unsure.
After narrowing down the choices, analyze each remaining option to ensure it aligns with your knowledge and reasoning. If you encounter a question that seems complex, look for patterns or connections to concepts you know well. Don’t be afraid to revisit the question later if time allows, as sometimes the answer will become clearer after tackling other questions.
Additionally, try to avoid getting caught up in “trick” answers. Many tests are designed with answers that may look correct at first glance but do not fully satisfy the conditions of the problem. By staying methodical and double-checking your work, you can minimize the chances of being misled.
Steps to Approach Multiple Choice Questions Read the question carefully Eliminate obviously incorrect answers Analyze remaining options Revisit the question if necessary Avoid “trick” answers By following these strategies, you will increase your chances of success in answering multiple choice questions correctly. Stay calm, think critically, and trust your preparation as you work through each question methodically.
Building Confidence Before the Test
Preparing for a challenging assessment can often bring about feelings of uncertainty and nervousness. However, building confidence before the test is a key factor in achieving success. A confident mindset not only enhances your performance but also reduces anxiety, allowing you to approach each question with clarity and focus. Confidence comes from effective preparation, a positive attitude, and a few strategic practices.
To strengthen your confidence, start by thoroughly reviewing key concepts and practice problems. Knowing that you’ve prepared well can significantly ease your nerves. Additionally, testing yourself under timed conditions will help simulate the pressure of the actual exam and make you more comfortable when the time comes. The more familiar you are with the structure of the questions and the timing, the less likely you are to feel overwhelmed.
Another important aspect is maintaining a positive attitude. Avoid self-doubt and instead focus on your strengths. Remind yourself of the progress you’ve made and the effort you’ve invested in your preparation. It’s also helpful to visualize success; imagine walking into the test center feeling calm, capable, and ready to tackle any challenge.
Key Practices to Build Confidence
Practice Description Review Key Concepts Ensure you understand the main topics and formulas that may appear on the test. Simulate Test Conditions Take practice tests within the time limits to get accustomed to the pressure. Positive Visualization Visualize yourself succeeding to foster a confident mindset. Focus on Progress Remind yourself of the improvements you’ve made during your preparation. Additional Tips for Test Day
On the day of the test, ensure you get a good night’s sleep and eat a healthy breakfast to boost your energy levels. Arriving early at the test location allows you to settle in and mentally prepare before the exam starts. Taking deep breaths and maintaining a calm demeanor will also help you focus and prevent unnecessary stress.
By incorporating these strategies into your preparation, you’ll not only boost your confidence but also maximize your chances of success on the test. Trust in your preparation, stay positive, and walk into the exam room ready to perform at your best.