Algebra Connections Chapter 7 Answer Key Guide

In this section, we delve into critical mathematical principles that form the foundation of problem-solving techniques. The content covers a variety of topics, each designed to build upon the previous ones, helping students refine their skills and deepen their understanding.

Problem-solving strategies are essential as they guide learners through complex scenarios. By applying these strategies, students can approach unfamiliar problems with confidence and accuracy, mastering each concept step by step. These methods focus on simplifying intricate ideas, making them more accessible and manageable.

Whether you’re grappling with equations or working on complex tasks, this guide offers practical solutions that not only clarify difficult material but also provide a clear path toward mastering essential skills. With a focus on clarity and precision, you’ll find the tools necessary to succeed in any mathematical challenge.

Algebra Connections Chapter 7 Answer Guide

This section is designed to help you navigate through the key concepts and problems in the seventh unit of your mathematical course. Here, you’ll find step-by-step instructions that break down complex problems into manageable tasks, allowing you to build a strong understanding of the material.

Each solution is explained clearly, showing the thought process and reasoning behind every step. By following these instructions, you will learn not only how to reach the correct result but also why each method is used, ensuring that you develop a deeper grasp of the techniques involved.

Whether you are tackling equations, working through geometric patterns, or solving real-world problems, this guide serves as a comprehensive resource. With detailed explanations, you will be able to approach problems with confidence, improving both your skills and your performance.

Understanding Key Concepts in Chapter 7

This section focuses on breaking down the fundamental principles that underpin the problems and exercises in this unit. Understanding these core ideas is crucial for tackling complex problems with confidence. By grasping these concepts, you’ll be able to connect various mathematical topics and apply them effectively in different scenarios.

Important Topics Covered

Solving and simplifying expressions
Working with equations and their solutions
Understanding geometric relationships
Analyzing patterns and sequences
Graphical representations of mathematical relationships

Key Strategies for Success

Start with the basics: Master simple techniques before moving on to complex problems.
Practice regularly: Repetition helps reinforce concepts and improves problem-solving speed.
Understand the reasoning: Focus on the “why” behind each solution, not just the final answer.
Visualize the problem: Use graphs or diagrams to better understand abstract ideas.

By familiarizing yourself with these key areas and approaches, you’ll have the foundation needed to solve more advanced problems as the course progresses. This section serves as a vital step in strengthening your mathematical abilities and applying them efficiently across various contexts.

Step-by-Step Solutions for Algebra Problems

This section provides a clear, structured approach to solving mathematical challenges, breaking down each problem into manageable steps. The goal is to simplify complex tasks, enabling learners to follow along with ease and fully understand the process behind each solution.

Below is an example of how to approach a typical problem methodically:

Step	Action	Explanation
1	Identify the equation	Start by writing down the given equation and understanding what is being asked.
2	Simplify terms	Combine like terms or simplify fractions to make the equation easier to solve.
3	Isolate variables	Move terms to one side of the equation to isolate the variable of interest.
4	Apply operations	Perform necessary operations (addition, subtraction, multiplication, division) to solve for the variable.
5	Check the solution	Substitute the solution back into the original equation to verify its accuracy.

By following this process, you can systematically tackle various problems, ensuring that each step is understood and executed properly. This method not only helps in solving individual questions but also builds a foundation for tackling more complicated mathematical tasks in the future.

Mastering Equations in Chapter 7

In this section, we focus on developing a strong understanding of how to solve different types of mathematical equations. Mastery of these skills is crucial, as equations form the foundation for solving more complex problems across various topics. With the right approach, you can easily tackle both linear and non-linear equations with confidence.

Step-by-step strategies are essential when working with equations. These methods help simplify the process, breaking down each part of the equation and making it easier to isolate variables. By practicing regularly, you can quickly identify patterns and apply the most effective solution techniques.

Key techniques include simplifying expressions, using substitution methods, and understanding the relationships between different terms. By becoming familiar with these strategies, you’ll gain the ability to approach even the most challenging equations with ease, ensuring greater success in your mathematical journey.

Tips for Solving Algebraic Expressions

When working with mathematical expressions, a systematic approach can help simplify complex problems and lead to accurate solutions. Understanding the rules and applying them consistently allows you to manipulate and solve expressions more effectively.

Key Techniques to Follow

Identify like terms: Combine terms that have the same variable and exponent.
Use distributive property: Apply distribution to eliminate parentheses in expressions.
Simplify fractions: Reduce fractions whenever possible to make the expression simpler.
Keep equations balanced: Perform the same operation on both sides of the equation.

Helpful Strategies

Start with the most complex terms and work towards simplifying the rest.
Check for opportunities to factorize or expand expressions for easier manipulation.
When in doubt, break the problem into smaller parts and solve each part step by step.

By following these tips, you’ll improve your ability to handle various expressions and become more efficient in solving even the toughest problems. Consistent practice will help reinforce these techniques, making them second nature when you encounter more challenging tasks.

Common Mistakes to Avoid in Algebra

While working through mathematical problems, certain mistakes can easily occur, often leading to confusion or incorrect results. Recognizing these common errors can save time and ensure more accurate solutions. By being aware of where things typically go wrong, you can take steps to avoid pitfalls and improve your problem-solving skills.

Frequent Errors to Watch Out For

Misinterpreting the order of operations: Always follow the correct sequence–parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
Forgetting to distribute properly: Ensure that when distributing a term across parentheses, every term inside the parentheses is affected.
Incorrectly combining unlike terms: Only terms with the same variable and exponent can be combined. Be careful not to mix them up.
Neglecting to check for extraneous solutions: When solving equations, always substitute solutions back into the original problem to verify their validity.

How to Prevent These Mistakes

Double-check your calculations at each step.
Review the basic rules of operations and make sure you’re applying them correctly.
Use a systematic approach to ensure that no steps are skipped or overlooked.

By being mindful of these errors and adopting a careful approach, you can avoid many common mistakes and gain more confidence in solving problems accurately.

How to Approach Word Problems

Word problems often seem intimidating because they require translating real-life situations into mathematical expressions. However, breaking down the problem into smaller, more manageable parts can help you approach it methodically and solve it with confidence. Understanding the key information and focusing on what is being asked is crucial for finding the right solution.

Steps for Solving Word Problems

Read the problem carefully: Understand all the details and highlight important information.
Identify what is being asked: Focus on what the problem wants you to find or calculate.
Assign variables: Define symbols or variables for unknown quantities in the problem.
Set up an equation: Translate the word problem into a mathematical expression or equation.
Solve the equation: Apply appropriate techniques to find the value of the unknowns.
Verify the solution: Substitute the solution back into the original problem to check its correctness.

Common Pitfalls to Avoid

Skipping important details: Missing even a small piece of information can lead to incorrect results.
Misinterpreting the question: Ensure you fully understand what the problem is asking before proceeding.
Overcomplicating the problem: Keep the solution as simple as possible–focus on the basic steps and methods.

By following these steps and practicing regularly, you can improve your ability to solve word problems and apply mathematical reasoning to real-world scenarios with ease.

Breaking Down Complex Algebra Topics

Many mathematical concepts can seem overwhelming at first glance, especially when they involve multiple steps or abstract ideas. However, by breaking them down into smaller, more digestible parts, you can approach them with a clearer understanding and greater confidence. Tackling these complex topics one step at a time allows you to grasp the fundamental principles and apply them effectively to more challenging problems.

Approach to Simplifying Complex Ideas

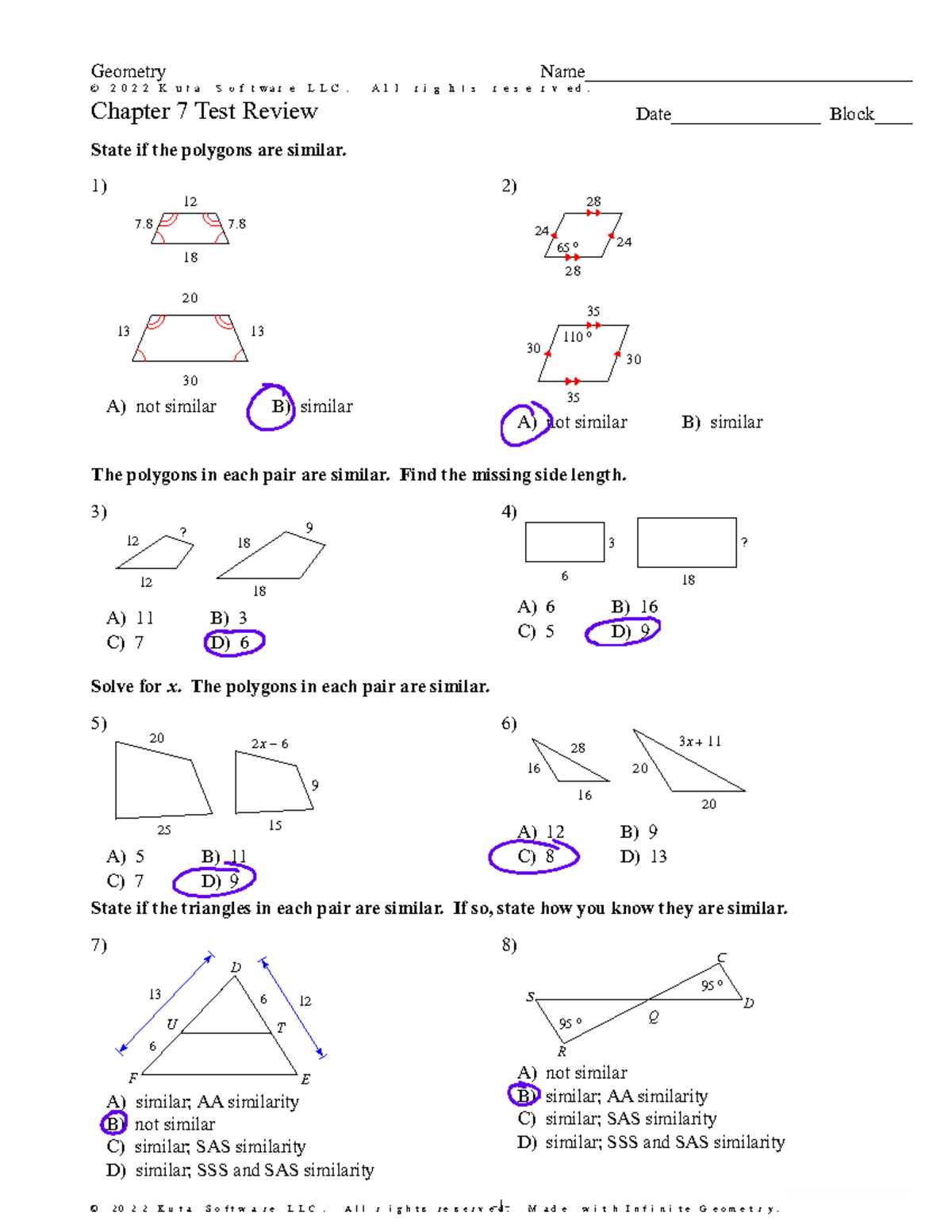
Start with the basics: Understand the foundational concepts before moving to more advanced topics.
Identify key patterns: Look for similarities between different types of problems to spot useful strategies.
Work through examples: Apply the concepts to practice problems, reinforcing understanding with real-world examples.
Use visual aids: Diagrams and graphs can often help clarify complex relationships between variables.

Strategies for Mastering Challenging Topics

Break problems into smaller steps: Simplify each part of the problem before combining them for the final solution.
Practice regularly: Repetition builds familiarity, helping you apply concepts quickly and accurately.
Seek alternative explanations: If a concept is unclear, try finding different methods or examples that explain it in a new way.

By breaking down complex topics into manageable sections and using a methodical approach, you can demystify even the most challenging concepts. Consistent practice and focused effort will enable you to tackle advanced problems with ease and accuracy.

Graphing Techniques for Chapter 7

Graphing is a powerful tool for visualizing mathematical relationships and solving problems involving equations or inequalities. By plotting data points and understanding how variables interact, you can quickly identify trends, solutions, and patterns. Mastering graphing techniques is essential for accurately interpreting and solving complex problems.

Basic graphing principles include plotting points on a coordinate plane, recognizing the structure of linear and non-linear graphs, and understanding the significance of slopes and intercepts. Each graph tells a story about the relationship between variables, and learning to read and interpret these graphs is key to solving problems efficiently.

Advanced techniques may involve graphing quadratic functions, finding the vertex, and understanding how transformations affect the shape of the graph. Mastery of these methods will allow you to approach more intricate problems with confidence and accuracy.

Practice Problems for Skill Building

Practicing mathematical problems regularly is crucial for strengthening your skills and improving your problem-solving abilities. By consistently working through a variety of exercises, you can build a deeper understanding of key concepts and enhance your ability to apply them in different situations. The more problems you solve, the more confident and proficient you’ll become in tackling complex tasks.

Effective Practice Strategies

Start with simpler problems: Begin with basic exercises to reinforce your understanding of fundamental principles.
Gradually increase difficulty: As you gain confidence, challenge yourself with more complex problems to further develop your skills.
Focus on different types of problems: Practice a wide range of problems to ensure you’re comfortable with various techniques and methods.
Check your work: After solving each problem, verify your solution to ensure accuracy and identify any mistakes.

Types of Problems to Practice

Linear equations and inequalities
Systems of equations
Quadratic expressions and functions
Word problems involving real-life scenarios

Consistent practice not only helps reinforce what you’ve already learned but also builds the confidence to approach new challenges. Embrace mistakes as learning opportunities and use each problem to refine your understanding and problem-solving strategies.

Exploring Systems of Equations

Systems of equations provide a powerful way to solve problems involving multiple unknowns. These sets of equations work together, each offering a piece of the puzzle to find the values of the variables that satisfy all conditions simultaneously. Whether you are dealing with two or more equations, understanding how to solve these systems is essential for tackling more complex mathematical challenges.

There are various methods to solve a system of equations, including graphing, substitution, and elimination. Each method has its advantages depending on the context of the problem. By mastering these techniques, you can efficiently solve systems and understand the relationships between the equations.

When solving such problems, it’s important to determine whether the system has a unique solution, no solution, or infinitely many solutions. Each scenario requires a different approach, and recognizing the type of system you’re dealing with will help guide your strategy for finding the correct answer.

Algebraic Strategies for Success

Achieving success in solving mathematical problems often requires a combination of strategy, understanding, and practice. By using a systematic approach to problem-solving, you can break down complex equations and uncover solutions with greater ease. Implementing proven techniques and honing problem-solving skills will lead to greater proficiency and confidence in handling diverse mathematical challenges.

Key Techniques for Problem-Solving

Understand the problem thoroughly: Before jumping into solving, take time to comprehend the question fully and identify the key components.
Work step-by-step: Break down each equation into smaller, manageable parts to avoid feeling overwhelmed.
Check your work: After reaching a solution, always revisit your calculations to ensure accuracy and consistency with the given information.

Helpful Approaches for Complex Problems

Visualize the problem: When possible, sketch a diagram or graph to provide a clearer perspective on the relationships between variables.
Use substitution or elimination: These techniques can help simplify systems of equations by isolating variables or eliminating unnecessary terms.
Seek patterns and connections: Identifying recurring trends or relationships can often reveal shortcuts or simplified methods for finding solutions.

By applying these strategies consistently and practicing regularly, you can master the techniques needed to solve increasingly challenging problems. The key to success lies in developing a strategic mindset and refining your problem-solving approach with each new exercise.

Real-Life Applications of Algebra

Mathematical concepts are not confined to the classroom–they are used extensively in the real world to solve practical problems. The ability to understand and manipulate variables, equations, and functions is essential in a wide variety of fields. From finance and engineering to science and technology, these mathematical tools help professionals make informed decisions and find effective solutions.

Common Fields Where Mathematical Techniques Are Applied

Finance: Budgeting, investing, and analyzing financial trends rely heavily on understanding equations that model growth or depreciation.
Engineering: Designing structures and machines involves solving systems of equations and optimizing designs for maximum efficiency.
Technology: Coding, algorithms, and data analysis all require mathematical modeling to process and interpret large amounts of information.
Science: Chemistry, physics, and biology frequently use equations to describe phenomena like chemical reactions, motion, and population growth.

Example: Using Equations in Finance

Scenario	Equation	Application
Loan Payment Calculation	PMT = P * (r(1 + r)^n) / ((1 + r)^n – 1)	To calculate monthly payments for a loan, where P is the principal, r is the interest rate, and n is the number of periods.
Investment Growth	A = P(1 + r/n)^(nt)	To determine the future value of an investment based on initial amount, rate, and time period.

By recognizing the many real-life applications of mathematical concepts, individuals can develop a greater appreciation for their utility and relevance. Whether it’s designing products, making financial decisions, or analyzing scientific data, mathematical skills are indispensable for success in many areas of life.

How to Check Your Answers

Verifying the accuracy of your solutions is a crucial step in problem-solving. Whether you’re dealing with equations or complex problems, it’s important to confirm that your results are correct. A systematic approach to checking your work can prevent costly errors and provide confidence in your answers. By following a few simple steps, you can ensure that you haven’t missed anything and that your solution is valid.

Key Steps to Verify Your Work

Revisit the Original Problem: Before double-checking your solution, review the original question to ensure you understand what is being asked and the required format of your answer.
Substitute Your Solution Back: If possible, substitute your solution back into the original equation to verify that both sides match. This is especially useful in equations involving variables.
Look for Patterns: Check if your answer makes sense logically. Does it follow expected trends or patterns based on the problem’s context?

Example: Checking Solutions in Equations

Step	Description	Example
Substitution	Substitute the solution into the original equation to confirm both sides are equal.	For the equation 2x + 3 = 7, if x = 2, check if 2(2) + 3 = 7.
Verification	Recalculate or use an alternate method to ensure the correctness of the solution.	For x = 2, 2(2) + 3 = 4 + 3 = 7, which matches the original equation.

By regularly implementing these checking techniques, you can minimize errors and ensure that your solutions are reliable and accurate. Verifying your results is not only a safeguard but also an opportunity to reinforce your understanding of the problem-solving process.

Using Software and Tools for Problem Solving

In today’s digital world, there are numerous tools and software programs available to assist with mathematical problem-solving. These tools can simplify complex calculations, help visualize data, and even provide step-by-step solutions to various types of problems. Whether you are a student looking to check your work or a professional in need of a quick solution, these resources can be incredibly valuable for enhancing your understanding and efficiency.

Popular Tools for Mathematical Assistance

Graphing Calculators: These devices allow users to plot graphs, solve equations, and analyze data. Graphing calculators are particularly useful for visualizing mathematical relationships and checking solutions.
Online Solvers: Websites and apps like Wolfram Alpha and Mathway offer real-time solutions for a wide range of mathematical problems. Simply input the equation, and the tool provides an answer, along with a detailed solution process.
Mathematical Software: Programs like MATLAB, GeoGebra, and Mathematica offer powerful features for advanced calculations, graphing, and modeling, making them ideal for higher-level studies or professional work.

How to Use These Tools Effectively

Understand the Problem: Before using any software, make sure you have a clear understanding of the problem you are solving. This will help you select the appropriate tool and avoid confusion when interpreting results.
Check for Accuracy: While these tools can be very helpful, always verify the results. Cross-check with manual calculations or consult your textbook to confirm the solution.
Explore Different Features: Many tools offer a variety of functionalities, such as graphing, solving systems of equations, or simplifying expressions. Take the time to explore and understand these features to get the most out of the software.

By incorporating these tools into your problem-solving process, you can streamline your work, save time, and improve your understanding of mathematical concepts. Whether you’re studying for an exam or tackling a complex problem at work, the right software can be an invaluable asset in your toolkit.

Reviewing Key Formulas and Theorems

Understanding fundamental formulas and theorems is essential for solving mathematical problems efficiently. These rules serve as the building blocks for more complex concepts and help you navigate through calculations with greater ease. By reviewing and familiarizing yourself with these core principles, you can approach problems with more confidence and accuracy. In this section, we will focus on some of the most important equations and theorems that play a crucial role in problem-solving.

Essential Formulas to Remember

Linear Equation: The general form of a linear equation is ax + b = 0, where a and b are constants, and x is the variable. This formula helps you find the value of x by isolating the variable on one side.
Quadratic Formula: The quadratic formula, x = (-b ± √(b² – 4ac)) / 2a, is used to solve second-degree polynomial equations. It provides the solutions for x in any quadratic equation of the form ax² + bx + c = 0.
Exponent Rules: Important rules for working with exponents include x^m * x^n = x^(m+n) and (x^m)^n = x^(m*n). These formulas simplify the multiplication and division of exponential expressions.

Key Theorems to Apply

The Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. This is expressed as a² + b² = c², where a and b are the legs, and c is the hypotenuse.
Distributive Property: The distributive property allows you to multiply a number by a sum or difference, expressed as a(b + c) = ab + ac. This rule is fundamental for simplifying expressions and solving equations.
Zero Product Property: If the product of two factors is zero, then at least one of the factors must be zero. In other words, if ab = 0, then a = 0 or b = 0.

By mastering these formulas and theorems, you’ll be better equipped to tackle a wide range of problems. Regular practice and application of these principles will help reinforce your understanding and improve your problem-solving skills.

Preparing for Exams in Mathematics

Effective preparation for exams in mathematics requires a clear strategy and consistent practice. Understanding the underlying concepts, reviewing key formulas, and practicing problem-solving are essential steps to ensure success. By following a structured approach, you can boost your confidence and performance during the exam. This section outlines several techniques to help you prepare efficiently and effectively for any upcoming tests.

Steps to Take Before the Exam

Review Core Concepts: Go over the key topics covered throughout the course. Focus on understanding the core principles behind each type of problem. If you are unsure about certain topics, review your notes and textbooks for clarification.
Practice Regularly: The more you practice, the more comfortable you become with various problem types. Make use of practice questions, past exams, and online resources to test your understanding.
Identify Weak Areas: Identify any areas where you may be struggling and focus additional time on these topics. Seek help from a teacher, tutor, or study group if necessary to address any gaps in your knowledge.

Effective Study Techniques

Create a Study Schedule: Plan your study sessions to ensure that you cover all topics in a structured manner. Set specific goals for each session, focusing on one topic at a time.
Work in a Distraction-Free Environment: Find a quiet, well-lit space to study, free from distractions. This will help you concentrate and retain information more effectively.
Use Active Learning: Engage with the material actively by solving problems, teaching concepts to others, or summarizing what you’ve learned. Active learning helps reinforce understanding and retention.

By following these preparation tips, you can build a strong foundation of knowledge and improve your problem-solving abilities, ensuring a more confident and successful exam experience.

Additional Resources for Chapter 7

To fully grasp the concepts and techniques covered in this section, it is essential to make use of supplementary materials that enhance your understanding and problem-solving skills. These resources provide various methods of support, from online tools to textbooks, that help clarify difficult topics and offer additional practice opportunities. Whether you’re looking for further explanations, practice problems, or interactive learning, these resources will aid you in mastering the material.

Online Tools and Websites

Khan Academy: An excellent resource offering free lessons on a wide range of topics. It includes video tutorials, exercises, and detailed explanations to reinforce key concepts.
Wolfram Alpha: A powerful computational engine that can solve mathematical problems step by step. It is useful for checking answers and understanding the solving process.
Desmos: An interactive graphing calculator that allows you to visualize equations and explore their behavior. This tool is helpful for understanding graphical representations of mathematical concepts.

Books and Study Guides

Math Textbooks: Review your textbook for more in-depth explanations and practice exercises related to the topics in this section. Many textbooks provide step-by-step solutions and additional examples to solidify your understanding.
Study Guides and Workbooks: Various study guides and workbooks are available that focus specifically on problem-solving strategies and practice problems. These resources often include tips and tricks for simplifying complex problems.
Instructor’s Notes: Don’t forget to refer to your instructor’s notes and class materials. These often highlight important areas to focus on and provide custom exercises tailored to the course content.

Utilizing these additional resources can provide you with a deeper understanding, improve your problem-solving skills, and prepare you thoroughly for any assessments. Whether through interactive tools, supplementary reading, or additional practice, these resources are invaluable in your learning journey.