Algebra Exam Answers Tips and Solutions for Success

Preparing for a challenging assessment in mathematics often requires more than just memorizing formulas. It’s essential to develop a deep understanding of the concepts and practice applying them in various scenarios. Mastery comes from not only solving individual problems but also from being able to approach them in different ways, using diverse strategies and techniques.

Effective preparation involves breaking down complex problems into simpler steps, recognizing patterns, and building confidence through consistent practice. Whether you’re tackling basic equations or advanced calculations, the key lies in understanding the logic behind each solution and being able to identify the best method for each situation.

Achieving success in such assessments is less about rote learning and more about honing problem-solving skills. With the right tools and mindset, you can confidently approach any challenge and find the path to a correct solution, no matter how difficult it may seem at first.

Algebra Exam Answers Guide

Preparing for a math assessment requires more than just understanding theoretical concepts; it’s about knowing how to approach each problem efficiently and accurately. This section will help you navigate through various types of problems, offering strategies to solve them step by step. The key is to develop a clear method for each type of challenge, ensuring you can handle anything that comes your way with confidence.

Each problem may require a different technique, but with consistent practice and the right approach, you can excel in any test scenario. Here’s a breakdown of essential techniques for tackling mathematical challenges:

Problem Type	Recommended Strategy	Key Tips
Linear Equations	Solve for the unknown by isolating the variable.	Check both sides of the equation for consistency.
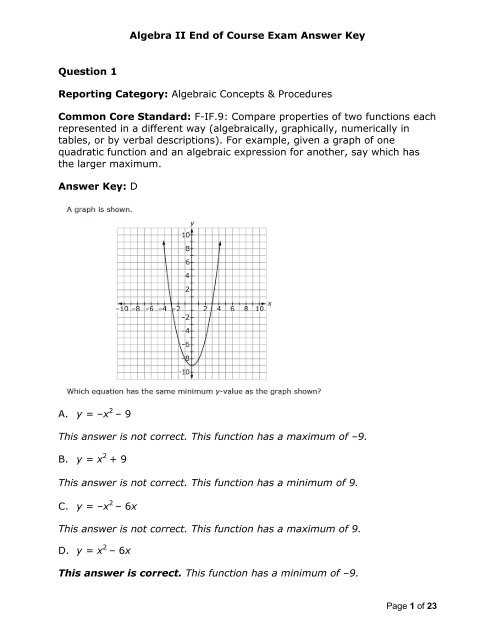
Quadratic Equations	Use factoring, completing the square, or the quadratic formula.	Remember the discriminant to determine real solutions.
Systems of Equations	Use substitution or elimination methods.	Ensure the equations are balanced before solving.
Inequalities	Solve the inequality similar to an equation, but reverse signs when multiplying/dividing by negative values.	Graph the solution on a number line to visualize the result.
Word Problems	Translate the word problem into an equation and solve.	Look for key words that indicate mathematical operations.

By mastering these strategies, you can approach your next challenge with a clear and focused mindset, ensuring you’re prepared for any type of question that may arise. Regular practice is essential, but understanding the methods behind each type of problem will give you the flexibility to adapt to different test scenarios.

Understanding Common Algebra Exam Questions

One of the most important steps in preparing for a mathematical assessment is recognizing the types of problems you are likely to encounter. Each question type tests a specific skill, and understanding these patterns is crucial for effective problem-solving. By familiarizing yourself with the most common question formats, you can approach each problem with a clear strategy in mind.

Key question types often revolve around solving equations, simplifying expressions, or interpreting word problems. These tasks are designed to assess your ability to apply fundamental concepts in various contexts. Whether you are dealing with linear relationships, solving for unknowns, or analyzing data, the core principles remain the same.

Familiarizing yourself with these questions allows you to identify the most efficient approach and avoid common pitfalls. With enough practice, recognizing the structure of a problem becomes second nature, enabling you to tackle more complex scenarios with ease. This understanding not only boosts your confidence but also helps you manage time effectively during a test.

Effective Strategies for Solving Algebra Problems

Mastering the art of solving mathematical problems involves more than just knowing formulas or procedures. It requires developing an approach that can be applied to a wide variety of challenges. By understanding the fundamental principles and following systematic methods, you can efficiently tackle complex questions and arrive at accurate solutions.

One of the most effective strategies is breaking down each problem into smaller, more manageable steps. This method not only simplifies the process but also helps avoid errors. Another crucial technique is identifying the type of problem at hand, as different questions may require specific approaches, such as substitution, elimination, or factoring.

It’s also important to approach each task with a clear plan in mind. Taking time to analyze the problem, organize your thoughts, and carefully execute each step leads to more consistent success. Regular practice with different problem types will further enhance your skills, allowing you to adapt quickly and solve even the most challenging questions.

Step-by-Step Solutions for Algebraic Expressions

Solving mathematical expressions requires a systematic approach to ensure accuracy. By breaking down each problem into logical steps, you can simplify the process and arrive at the correct solution with confidence. In this section, we will explore the best practices for tackling expressions and offer clear instructions for handling them efficiently.

Understanding the Problem

The first step in solving an expression is to fully understand the problem. Carefully read through the problem and identify the components you are working with. Are there any constants, variables, or operations involved? Understanding these elements will help you determine the approach to take.

Breaking Down the Steps

Once you have a clear understanding of the problem, follow these key steps to simplify and solve the expression:

Combine like terms: Group terms with the same variable and simplify them.
Apply operations: Use addition, subtraction, multiplication, or division as needed to simplify the expression.
Isolate the variable: If solving for a specific variable, move all terms involving it to one side of the equation.
Check for consistency: Ensure all operations are correctly performed and that the expression is fully simplified.

By following these steps, you can solve a variety of mathematical problems efficiently. With practice, the process will become more intuitive, allowing you to tackle increasingly complex challenges with ease.

How to Tackle Word Problems in Algebra

Word problems are often considered one of the most challenging types of mathematical questions. These problems require more than just technical skills; they also test your ability to interpret and translate a written scenario into a solvable equation. To effectively tackle such problems, it’s important to have a clear strategy for breaking down the information and identifying the key elements.

Breaking Down the Problem

The first step is to carefully read the problem and identify the important details. Look for numbers, relationships between variables, and the question being asked. Pay attention to words that indicate mathematical operations, such as “sum,” “difference,” “product,” or “quotient.” This will guide you in forming an equation that represents the situation.

Setting Up and Solving the Equation

Once you’ve translated the problem into an equation, follow these steps to solve it:

Identify the unknown: Determine what you need to find, and assign a variable to represent it.
Translate the words into math: Use the information given in the problem to form an equation with the appropriate operations.
Solve step by step: Simplify the equation by isolating the variable and performing the necessary operations.
Double-check your work: Review the problem to ensure that the solution makes sense in the context of the question.

With practice, this method will help you approach word problems with greater confidence and efficiency, turning complex scenarios into manageable steps.

Key Formulas You Need for Algebra Exams

In any mathematical assessment, having a solid understanding of key formulas is essential for solving problems quickly and accurately. These formulas serve as the foundation for various problem types and can simplify complex calculations. Knowing when and how to apply them is just as important as understanding their structure.

From linear equations to quadratic relationships, certain formulas are used repeatedly to find solutions. Being familiar with these will allow you to approach problems with a methodical process, increasing your efficiency and confidence during the test. Below are some of the most important formulas to remember:

Linear Equation: y = mx + b – This formula represents a straight line, where m is the slope and b is the y-intercept.
Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – Used to solve quadratic equations in the form ax² + bx + c = 0.
Slope Formula: m = (y₂ – y₁) / (x₂ – x₁) – Used to find the slope between two points on a graph.
Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²) – Used to calculate the distance between two points in a coordinate plane.
Area of a Triangle: A = ½ × base × height – Calculates the area of a triangle using its base and height.

Being able to recall and apply these formulas will significantly improve your problem-solving skills, ensuring you can handle a wide variety of questions with ease.

Common Mistakes to Avoid in Algebra Tests

When taking a math test, it’s easy to make small errors that can have a big impact on your final score. These mistakes often stem from rushing, misinterpreting a question, or overlooking important details. By being aware of the most common pitfalls, you can avoid them and improve your overall performance.

Key Mistakes to Watch Out For

While solving problems, there are a few frequent errors that students tend to make. These mistakes can range from simple calculation errors to misunderstanding the problem itself. Below are some of the most common mistakes and tips on how to avoid them:

Mistake	How to Avoid
Not reading the problem carefully	Always read the entire question before attempting to solve it. Identify key information and what is being asked.
Skipping steps in calculations	Work through each step methodically. Double-check your calculations and ensure no steps are skipped.
Incorrectly applying formulas	Familiarize yourself with key formulas, and make sure you’re using them in the right context. Pay attention to details like signs and variables.
Forgetting to check answers	Always check your work. Substituting your solution back into the original equation can help you verify your result.
Misunderstanding negative signs	Be cautious with negative numbers, especially when multiplying or dividing. Review the rules for handling negative signs in calculations.

Conclusion

Avoiding these common mistakes will help you approach problems more confidently and accurately. By practicing good habits and paying attention to detail, you can significantly improve your performance on any test.

Time Management Tips for Algebra Exams

Effective time management is crucial when tackling any mathematical assessment. Without a clear plan, it’s easy to get stuck on difficult questions or run out of time before completing the test. By allocating your time wisely and sticking to a strategy, you can maximize your performance and ensure that you have enough time to address every part of the test.

Prioritize and Plan

The first step in managing your time efficiently is to prioritize tasks. Start by assessing the questions, identifying the ones you can solve quickly, and leaving the more complex ones for later. Here are some tips to help with this:

Skim through the test: Quickly read through all the questions to get an overview. Identify the easier questions that you can answer in a short amount of time.
Allocate time per section: Estimate how long you should spend on each section of the test based on its difficulty and point value.
Leave complex problems for last: Tackle the simpler questions first to build confidence and secure easy points.

Efficient Problem-Solving Strategies

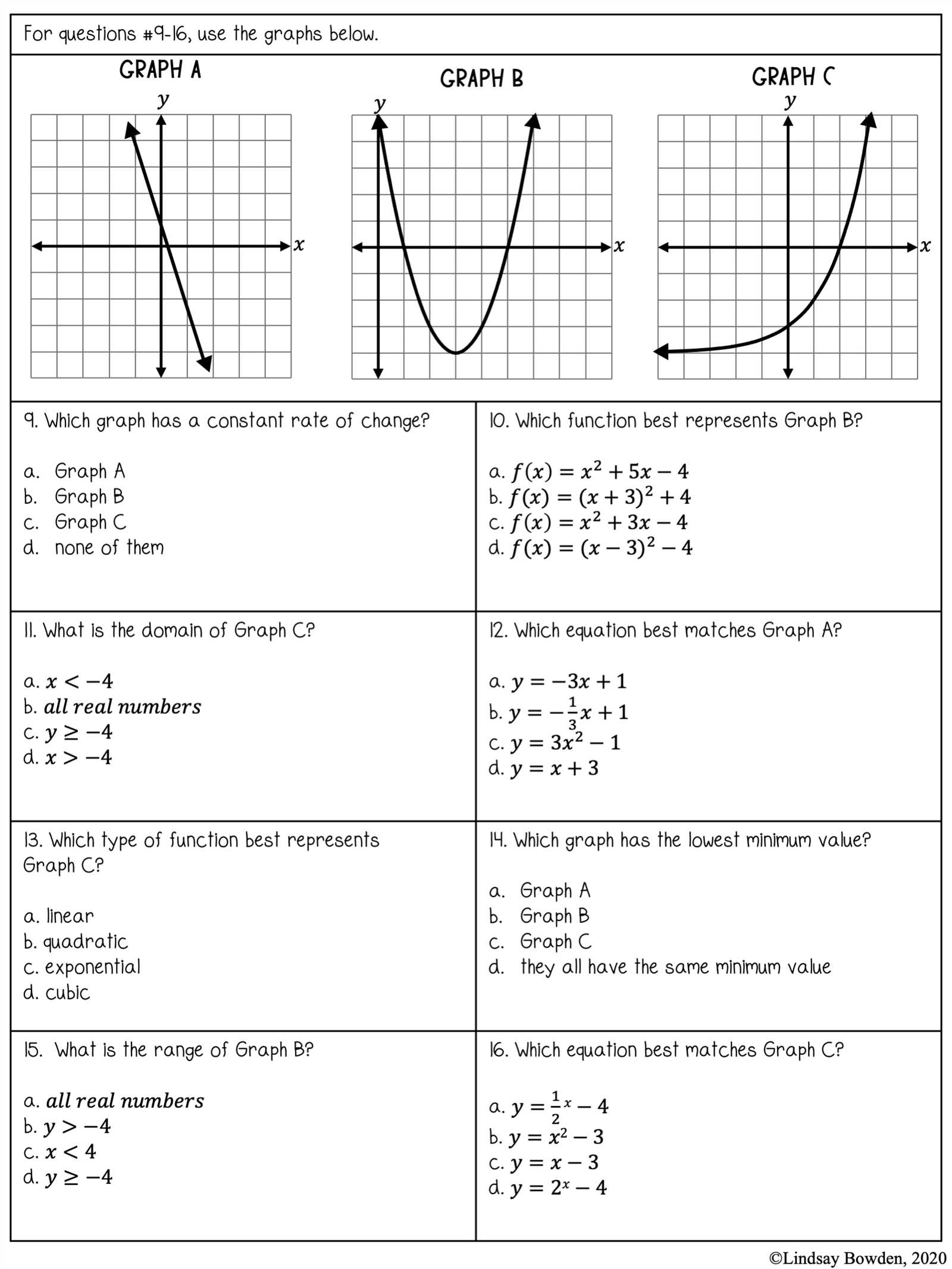
Once you’ve prioritized your questions, it’s time to apply strategies that allow you to solve them quickly and accurately. Below are some methods for managing time during the problem-solving process:

Work systematically: Break down each problem into smaller, manageable parts. This approach saves time and reduces the risk of errors.
Don’t dwell on one problem: If you’re stuck on a particular question, move on and come back to it later. Sometimes, taking a break helps you see things more clearly.
Check your work: Allocate a few minutes at the end of the test to review your answers. This will help you catch any mistakes and make sure your solutions are accurate.

By following these time management tips, you can ensure that you have enough time to complete every question thoughtfully and accurately, leading to better performance and less stress during the test.

Using Graphs to Solve Algebraic Problems

Graphs provide a powerful visual tool for solving mathematical problems, helping to represent relationships between variables clearly. By plotting equations or expressions on a graph, you can easily identify solutions, understand patterns, and make sense of complex data. This method transforms abstract numbers into a more tangible format, offering a deeper insight into the behavior of the problem.

When working with graphs, the x and y axes represent different variables, and the points plotted on the graph correspond to solutions of the equation. By analyzing the graph, you can find the intersection points, determine slopes, or evaluate trends. This can be particularly useful for problems involving linear or quadratic relationships.

Here are a few ways graphs can assist in solving problems:

Identifying Solutions: Graphs help to quickly find the point where two lines or curves intersect, which corresponds to the solution of a system of equations.
Visualizing Functions: By plotting functions on a graph, you can better understand how different variables relate to each other and predict future behavior.
Solving Inequalities: Graphs also allow for the visualization of inequalities, showing regions of solutions rather than specific points.
Finding Slope and Intercept: For linear equations, graphs make it easy to determine the slope and y-intercept, providing a clearer understanding of the equation’s behavior.

Using graphs to solve problems not only simplifies complex tasks but also helps to develop a more intuitive understanding of mathematical concepts. With practice, you can become more proficient at interpreting and drawing graphs, making it easier to solve similar problems in the future.

How to Approach Complex Algebraic Equations

When faced with complicated equations, it can be easy to feel overwhelmed. However, breaking down the problem into smaller, more manageable steps can make the process easier and more efficient. With a clear approach and methodical strategy, even the most complex equations can be solved systematically.

The key is to approach the problem step by step, using the appropriate techniques based on the structure of the equation. Whether you’re working with polynomials, rational expressions, or systems of equations, understanding the right method to apply is essential for simplifying the problem and finding the solution.

Here are some strategies to keep in mind when tackling challenging equations:

Start by Simplifying: Before jumping into solving, simplify both sides of the equation if possible. Combine like terms and remove unnecessary parentheses to make the equation clearer.
Use Substitution or Elimination: For systems of equations, substitution or elimination methods can simplify the process and lead to faster solutions.
Isolate Variables: In equations with multiple variables, work towards isolating the variable you are solving for. This can often simplify the equation and make it easier to solve.
Factor When Necessary: Factoring is an important technique that can simplify complex expressions, especially when dealing with quadratics or higher-order polynomials.
Check Your Work: Once you’ve arrived at a solution, substitute your answer back into the original equation to ensure its accuracy. This helps verify that no errors were made during the process.

By maintaining a calm, structured approach and applying these strategies, you can break down even the most complex equations into simpler components and solve them with confidence.

Improving Your Mathematical Skills Before the Test

Mastering complex mathematical concepts takes time and practice, especially when preparing for an important assessment. To improve your problem-solving abilities, it is crucial to build a solid foundation and reinforce your understanding of key concepts. By focusing on consistent practice and employing effective study techniques, you can boost your confidence and performance.

Here are several strategies to help sharpen your skills before the test:

Review Core Concepts: Make sure you have a clear understanding of fundamental principles such as equations, functions, and graphing. Strengthen your knowledge of key formulas and methods used in problem-solving.
Practice Regularly: The best way to improve is by solving as many problems as possible. This will not only help you become more familiar with different types of questions but also improve your speed and accuracy.
Break Down Complex Problems: If you come across a difficult problem, break it down into smaller parts. This can make the problem more manageable and prevent you from feeling overwhelmed.
Use Study Resources: Utilize textbooks, online tutorials, and practice tests to reinforce your knowledge. These resources often provide step-by-step solutions and additional examples that can deepen your understanding.
Work with a Study Group: Collaborating with peers can be extremely helpful. By discussing concepts and solving problems together, you can learn new strategies and gain fresh perspectives on challenging material.

By following these steps and staying committed to improving your skills, you’ll feel more prepared and confident when it comes time to take the test. Regular practice, along with the right strategies, will ensure you’re ready for anything that comes your way.

Analyzing Multiple-Choice Mathematical Questions

Multiple-choice questions are a common format in many assessments, offering a range of possible answers to choose from. While these questions may seem straightforward, they require careful analysis and a methodical approach to select the correct solution. By understanding the structure of these questions and applying strategic techniques, you can improve your chances of answering them correctly.

When tackling multiple-choice problems, it is important to focus not only on the question itself but also on the available options. Often, the wrong answers are designed to test common misconceptions, so recognizing these patterns can be incredibly useful.

Steps to Effectively Analyze Multiple-Choice Questions

Read the Question Carefully: Ensure you fully understand what the question is asking before looking at the answer choices. Highlight key information or terms that will guide your solution process.
Eliminate Obvious Incorrect Answers: Start by eliminating answers that are clearly wrong. This increases your chances of selecting the correct answer, even if you’re unsure about the remaining options.
Consider All Possible Choices: Sometimes, answers are very similar, but one has a subtle difference. Make sure you examine each option carefully and compare them to the problem’s requirements.
Test Your Answer: If time allows, substitute your answer back into the original equation or context to verify that it satisfies the problem. This step can help catch any mistakes in reasoning.

Common Strategies for Success

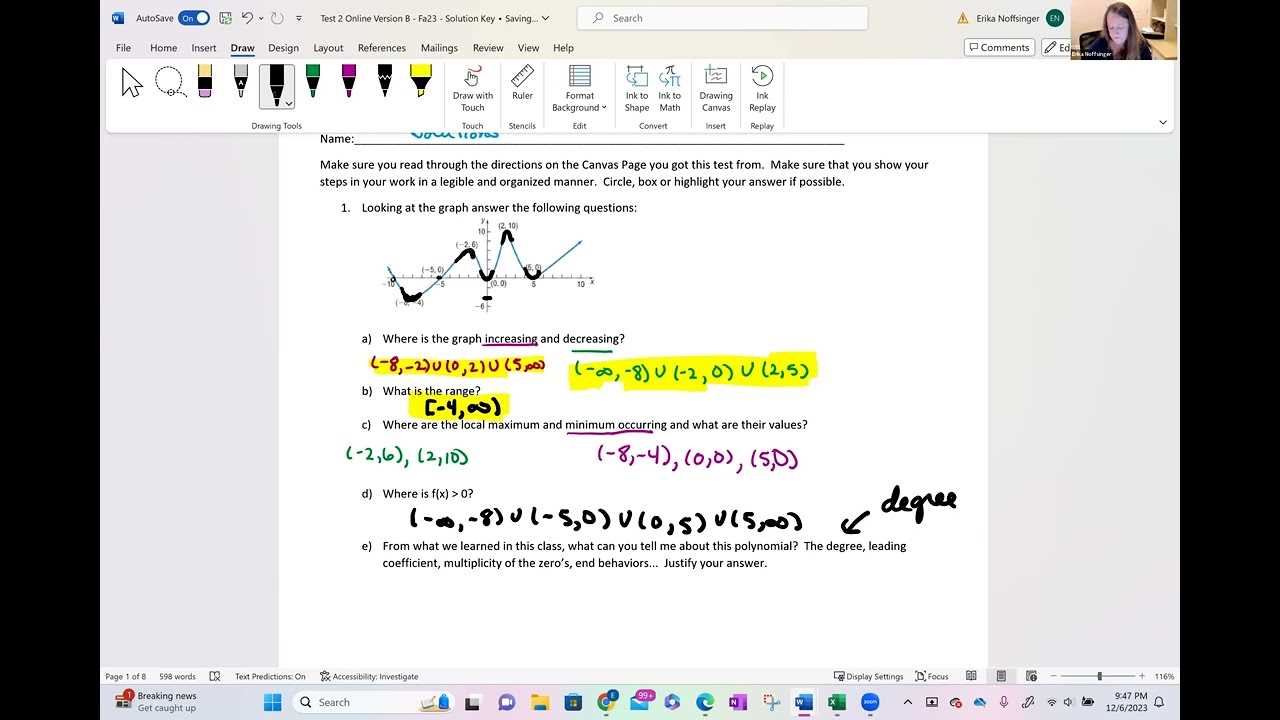
Look for Keywords: Certain words in the problem may hint at the correct approach or solution, such as “increase,” “decrease,” or “total.” Identifying these keywords can provide valuable insights.
Work Backwards: If you’re unsure about the solution, try plugging the answer choices into the problem. This can quickly help you find the correct solution.
Practice Makes Perfect: Regular practice with multiple-choice questions helps familiarize you with the format, improves your decision-making skills, and enhances your overall test-taking strategy.

By employing these techniques and practicing regularly, you’ll be able to approach multiple-choice problems with greater confidence and accuracy, ultimately improving your performance on similar questions.

Practice Tests for Mathematical Assessment Preparation

Practice tests are an essential tool for anyone preparing for a significant mathematical assessment. They simulate the actual testing environment and help identify areas where further review is needed. By taking multiple practice tests, you can build confidence, improve your problem-solving speed, and refine your approach to different types of questions. These tests allow you to familiarize yourself with the format and gain a deeper understanding of what to expect on test day.

Utilizing practice tests effectively can make a significant difference in your preparation process. Not only do they help you review content, but they also provide valuable feedback on your strengths and weaknesses, allowing you to tailor your study plan accordingly.

How Practice Tests Help

Boost Time Management Skills: Practice tests help you get used to the time constraints of an actual test. By simulating the real experience, you learn how to manage time efficiently and avoid spending too long on difficult questions.
Identify Knowledge Gaps: Taking these tests allows you to pinpoint areas where you may need additional study or practice, ensuring that you focus your efforts on the most important topics.
Build Confidence: The more you practice, the more confident you’ll feel in your ability to tackle the real assessment. Repeated exposure to different types of questions will reduce anxiety and improve your performance.

Creating a Practice Test Schedule

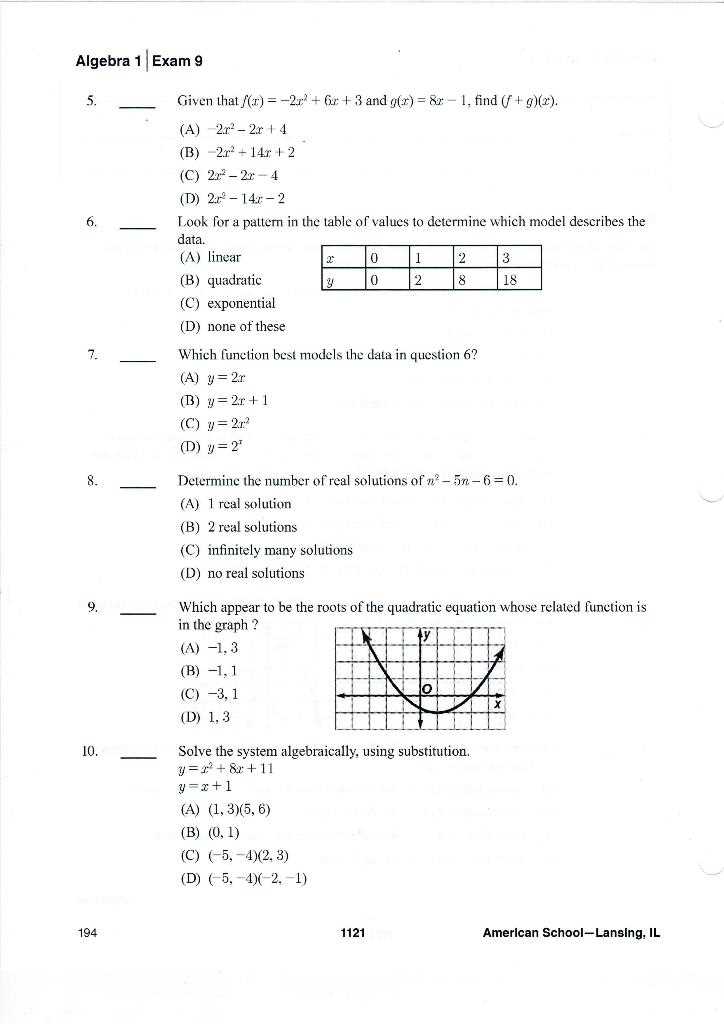
To maximize the benefits of practice tests, it’s important to create a structured schedule that aligns with your study plan. Here’s a simple guide:

Week	Action	Focus Areas
Week 1	Take a diagnostic test	Identify weak areas and set goals
Week 2	Complete practice test 1	Focus on basic problem-solving techniques
Week 3	Complete practice test 2	Review advanced topics and complex problems
Week 4	Complete final practice test	Focus on speed and accuracy

By following a dedicated practice test schedule, you can track your progress and ensure you’re well-prepared for the actual assessment. With consistent effort, these tests will help you become more familiar with the format, boost your test-taking skills, and increase your chances of success.

Why Word Problems Are Challenging

Word problems often pose a significant challenge for many learners due to the need to translate real-world situations into mathematical expressions. These types of questions require a combination of critical thinking, problem-solving skills, and the ability to recognize the underlying mathematical concepts hidden within the text. While straightforward numerical problems may seem easier, word problems involve a layer of complexity because they require understanding the context and framing the appropriate equation or method to solve it.

Additionally, word problems can sometimes be vague or involve extraneous information that distracts from the actual solution. The ability to sift through the information and focus on what is necessary is a key skill in approaching these problems effectively.

Key Challenges in Word Problems

Interpreting the Question: Word problems often present scenarios in everyday language, which can lead to confusion in determining what exactly is being asked. Identifying the main question and focusing on the critical details is essential.
Extracting Relevant Information: Many word problems contain unnecessary or misleading data that must be filtered out. The ability to discern which pieces of information are relevant is a crucial skill in solving these problems.
Choosing the Correct Approach: After understanding the problem, the next challenge is deciding which mathematical method or operation to apply. This can vary greatly depending on the structure of the problem and the concepts involved.

How to Overcome These Challenges

Practice Regularly: Consistent practice with word problems can improve your ability to identify patterns and refine your problem-solving techniques.
Break Down the Problem: When faced with a complex word problem, breaking it into smaller, more manageable parts can help. Focus on one step at a time, whether it’s identifying variables, setting up equations, or solving for the unknowns.
Visualize the Situation: Drawing diagrams or creating tables can help visualize the problem more clearly, making it easier to translate words into mathematical operations.

While word problems may initially appear intimidating, with practice and the right strategies, they can become more manageable. Developing strong problem-solving habits and improving your ability to interpret and analyze word problems will make you more confident and proficient in tackling them.

How to Double-Check Your Solutions

Ensuring the accuracy of your solutions is an essential part of problem-solving. It’s easy to make small errors while working through complex calculations, so taking time to review your work can help identify and correct any mistakes before finalizing your answer. Double-checking is not just about looking over your steps, but about verifying that each stage of your solution follows logically and is mathematically sound.

There are several strategies you can use to verify your results and ensure that your work is correct. The key is to approach the review process systematically and carefully. By retracing your steps, checking for consistency, and using different methods to confirm your solution, you can avoid common pitfalls and enhance the reliability of your answers.

Strategies for Verifying Your Work

Rework the Problem: Go through the entire process again, following the same steps. This will help you catch any calculation errors or overlooked details. Sometimes, a fresh look can reveal mistakes you missed the first time.
Check for Consistency: Ensure that your solution makes sense in the context of the problem. If the answer seems unreasonable or inconsistent with the given data, it may be worth revisiting the steps.
Substitute Your Solution Back: If your solution involves finding a value for an unknown, substitute that value back into the original equation or problem. If it holds true, you’ve likely arrived at the correct solution.

Additional Tips

Use Different Methods: Try solving the problem using an alternate method or approach. For example, if you used algebraic manipulation to solve an equation, try graphing or using a calculator to verify the results.
Ask for a Second Opinion: If possible, discuss your solution with someone else. A second pair of eyes can sometimes spot errors you might have missed.
Take Your Time: Rushing through the verification process can lead to overlooking errors. Make sure to review your work carefully and methodically.

By following these strategies and regularly double-checking your solutions, you can improve the accuracy of your problem-solving and gain more confidence in your results.

Top Tips from Successful Students

Achieving success in problem-solving challenges requires not just hard work, but also strategic preparation. Top students know that mastering complex concepts involves a combination of focus, time management, and smart approaches to problem-solving. By following their techniques, you can improve both your understanding and your performance when faced with difficult tasks.

The following tips are shared by students who have consistently excelled in their coursework and are proven to help improve efficiency, accuracy, and confidence. By adopting these methods, you can optimize your study habits and maximize your potential in solving mathematical challenges.

Time Management and Organization

Start Early: Successful students emphasize the importance of starting their preparation well in advance. This approach helps prevent last-minute cramming and provides time to deeply understand the material.
Break Down Tasks: Rather than tackling everything at once, break complex problems into smaller, manageable sections. This not only makes problems less overwhelming but also helps maintain focus.
Plan Your Study Sessions: Create a schedule and stick to it. Set specific times for studying, focusing on one topic or type of problem at a time.

Mastering Problem-Solving Techniques

Understand Key Concepts: Top performers focus on understanding the core principles behind each type of problem rather than memorizing formulas. This deeper understanding enables them to apply concepts to various situations with ease.
Practice Regularly: Consistent practice is key. Students who perform well often practice a variety of problems to strengthen their skills and improve their ability to approach unfamiliar challenges.
Review Mistakes: Review any errors carefully to understand where you went wrong. This self-reflection helps prevent the same mistakes in the future and improves overall problem-solving techniques.

By incorporating these tips into your study routine, you can improve not only your problem-solving skills but also your overall confidence in tackling complex tasks. Success comes with consistent effort and smart strategies, and top students have mastered the art of both.

Resources for Further Practice

Expanding your knowledge and improving problem-solving abilities requires consistent practice. While understanding the theory is important, applying what you’ve learned through additional exercises helps solidify those concepts and enhances your problem-solving skills. There are a variety of resources available that cater to different learning styles, offering diverse ways to reinforce your skills and boost your confidence.

In this section, we will explore several tools, websites, and platforms that provide comprehensive practice materials. These resources are designed to help learners of all levels, from beginners to more advanced students, to continue developing their expertise and tackling more challenging problems.

Online Platforms and Websites

Khan Academy: This free online resource offers lessons and practice problems on a wide range of topics. The step-by-step tutorials and exercises are perfect for reinforcing basic to advanced concepts.
Brilliant: Known for its interactive problem-solving approach, Brilliant offers guided lessons and challenges that encourage critical thinking and help improve your problem-solving abilities.
IXL Learning: IXL provides a comprehensive set of exercises with instant feedback, allowing you to track your progress and focus on areas that need improvement.

Books and Printed Materials

“Problem-Solving Strategies” by Arthur Engel: This book is an excellent resource for those looking to enhance their analytical and problem-solving skills. It provides a wide variety of problems with solutions, promoting independent learning.
“The Art of Problem Solving” series: This series offers a deep dive into mathematical thinking, providing readers with a broad range of exercises that develop both foundational and advanced problem-solving strategies.

These resources will help you to practice regularly and reinforce your understanding, giving you the confidence to approach any challenge with a strategic mindset. Whether you prefer interactive platforms, structured exercises, or printed materials, the right tools are available to support your growth.