Algebra Nation Section 1 Test Answers Guide

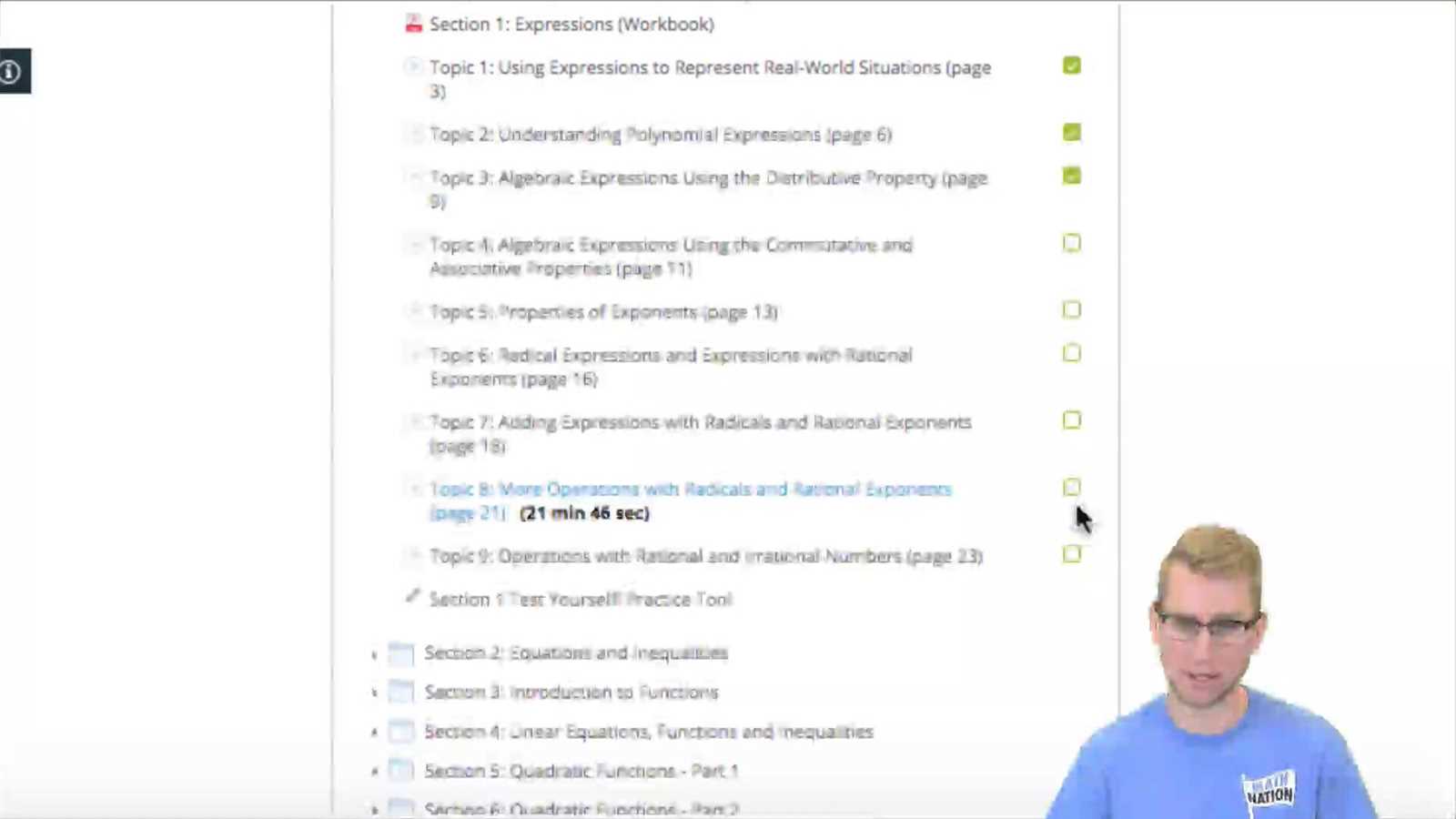
Mastering fundamental mathematical concepts is essential for achieving success in any academic environment. The first part of the curriculum focuses on building a strong foundation, helping learners grasp important principles that are critical for tackling more complex problems. By carefully reviewing the material and practicing regularly, students can increase their confidence and proficiency in these areas.

Preparation is key to understanding the core principles that are tested. Developing a clear grasp of the core ideas will make it easier to approach new challenges with clarity. The first chapter encourages learners to apply their knowledge step by step, breaking down larger problems into manageable parts.

Effective study techniques such as reviewing key formulas and practicing with sample problems can enhance retention and understanding. With consistent effort, learners will be well-equipped to navigate the various types of questions encountered in this initial phase of learning.

Algebra Nation Section 1 Test Overview

The first part of this learning module is designed to establish a strong foundation in mathematical concepts, offering learners an opportunity to familiarize themselves with the fundamental principles needed for solving more advanced problems. The content covered focuses on key skills and techniques essential for success in the later stages of the course. This section emphasizes clear understanding and application of basic rules, ensuring that students can move forward with confidence.

Core Areas of Focus

Understanding basic mathematical operations and their applications.
Identifying patterns and relationships between numbers.
Mastering essential problem-solving techniques for different types of questions.
Focusing on logical reasoning and analysis.

Approach to Learning and Mastery

In this phase, learners will be introduced to various techniques that help break down complex problems into manageable steps. Through practice and repetition, students will refine their skills and enhance their ability to recognize patterns and solve equations. The focus is on developing critical thinking and applying knowledge effectively in different scenarios.

Practice problems designed to reinforce key concepts.
Step-by-step explanations for better understanding.
Real-life applications to make the learning process more engaging.

Understanding Algebra Nation Test Format

This part of the learning module introduces the structure and layout of the assessment, allowing students to become familiar with how questions are presented. By understanding the format, learners can approach the task with greater confidence, knowing what to expect. The goal is to ensure that students can effectively apply their knowledge in the context of the challenges provided.

The format is designed to evaluate understanding through a variety of question types, each aimed at testing different skills. These may include multiple-choice questions, problem-solving exercises, and reasoning tasks, all structured to reflect real-world scenarios. The diversity of questions ensures a comprehensive assessment of the core concepts.

Familiarity with the format helps students manage their time effectively, ensuring that they can approach each question strategically. By practicing with similar structures, learners can refine their problem-solving techniques and improve their overall performance in future challenges.

Key Concepts Tested in Section 1

The first part of the learning process focuses on the essential principles that form the foundation for more complex topics. Mastery of these core concepts is crucial for progressing through the material, as they are frequently tested and applied in various problem-solving scenarios. These concepts are designed to strengthen your mathematical reasoning and improve your ability to work with numbers and equations effectively.

Core Ideas Evaluated

Operations with integers and rational numbers.
Understanding and applying basic formulas.
Recognizing and solving for variables in simple equations.
Manipulating expressions using fundamental arithmetic rules.

Skills Tested

Identifying and applying mathematical patterns.
Solving problems with a step-by-step approach.
Analyzing mathematical relationships and their implications.
Interpreting and solving word problems based on real-life situations.

How to Approach Algebra Nation Section 1

When tackling the first part of this module, it is essential to have a clear strategy to make the most of your learning. A methodical approach ensures that you are not only able to recall important information but also apply it effectively. Taking the time to understand the structure of the content and the types of questions asked will allow you to navigate the material with greater ease and confidence.

Step-by-Step Approach

Review Core Concepts: Begin by revisiting the foundational principles that form the basis of this section. Understanding these core ideas will allow you to address questions with more clarity.
Break Down Each Problem: Approach each question systematically. Identify the key elements and apply relevant techniques to solve it step by step.
Practice with Similar Problems: Work through practice exercises to build familiarity and reinforce your understanding of the material.
Double-Check Your Work: Once you have completed a problem, take a moment to review your solution for any possible errors.

Tips for Efficient Study

Stay Organized: Keep your notes and resources well-organized so you can easily refer to them when needed.
Focus on Key Areas: Prioritize topics that are more challenging or that appear more frequently in the material.
Manage Your Time: Set aside dedicated study time and practice under timed conditions to simulate the learning environment.

Important Algebra Rules to Remember

When working through mathematical challenges, understanding and applying the basic rules is crucial for solving problems correctly and efficiently. These fundamental principles help guide the process, ensuring that operations are carried out in the correct order and that equations are simplified accurately. Keeping these rules in mind will streamline your problem-solving approach and improve your overall performance.

Key Mathematical Rules

Order of Operations: Always follow the correct sequence–parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
Distributive Property: Multiply a number across terms in parentheses, such as a(b + c) = ab + ac.
Combining Like Terms: Combine terms that have the same variable and exponent, such as 3x + 2x = 5x.
Inverse Operations: Use the opposite operation to isolate variables in equations, such as adding the opposite to cancel out terms.

Advanced Concepts to Keep in Mind

Factoring: Breaking down expressions into simpler factors, such as x² – 9 = (x + 3)(x – 3).
Solving for Variables: Isolate the unknowns by performing the same operation on both sides of the equation.
Handling Fractions: Multiply or divide fractions carefully, ensuring you follow the correct steps for simplification.

Step-by-Step Solutions for Section 1

Breaking down complex problems into manageable steps is a key strategy for successfully navigating through mathematical exercises. By following a structured approach, you can ensure that each part of the problem is addressed thoroughly, reducing the risk of mistakes. The step-by-step process helps to simplify even the most challenging tasks, allowing you to focus on applying the correct techniques at each stage.

Solving Example 1

Identify the given values: Carefully read the problem and highlight the numbers and variables that are provided.
Apply the correct operation: Determine which mathematical operation is required–addition, subtraction, multiplication, or division.
Simplify the equation: Carry out the operation and simplify both sides, ensuring that you follow the proper rules.
Isolate the variable: If solving for an unknown, use inverse operations to isolate the variable on one side of the equation.
Verify the solution: Once the equation is solved, check your work by substituting the solution back into the original equation.

Solving Example 2

Start with the given equation: Write down the full equation before performing any operations.
Combine like terms: Group terms with the same variable and simplify them before moving forward.
Use the distributive property if needed: Apply multiplication over addition or subtraction where applicable to simplify the equation.
Check for any fractions: If fractions are involved, multiply both the numerator and denominator to simplify them.
Final solution: Solve the simplified equation and confirm that the answer makes sense when substituted back into the original problem.

Common Mistakes to Avoid in Section 1

When working through mathematical exercises, it’s easy to make small errors that can lead to incorrect results. These mistakes often arise from misunderstandings of the rules or from rushing through the steps without fully reviewing the problem. By being aware of these common pitfalls, learners can develop strategies to avoid them and ensure greater accuracy in their work.

Frequent Errors

Skipping the order of operations: Not following the correct sequence for performing operations can lead to incorrect results. Always remember to handle parentheses first, followed by exponents, multiplication, and division, and lastly, addition and subtraction.
Combining unlike terms: Grouping terms that don’t share the same variable or exponent will lead to errors. Only combine terms that are similar in nature.
Ignoring negative signs: Negative signs can be easily overlooked or misapplied, leading to wrong answers. Pay close attention to how they affect calculations, especially in multiplication and division.
Incorrectly applying the distributive property: Forgetting to distribute a term properly or making an error in multiplication can cause problems. Always distribute each term within parentheses carefully.

Other Mistakes to Avoid

Failing to check work: After completing an equation, skipping the step of double-checking can result in missed mistakes. Always review each solution before finalizing it.
Overcomplicating the problem: Sometimes, trying to make a problem harder than it is can lead to confusion. Focus on the basics and avoid overthinking the solution.
Misunderstanding the problem’s requirements: Not fully reading or interpreting the problem correctly can result in incorrect methods being used. Always ensure you understand what is being asked before proceeding.

Helpful Study Resources for Algebra Nation

Utilizing the right study tools can make a significant difference when preparing for mathematical exercises. Whether you prefer online platforms, textbooks, or practice worksheets, having access to a variety of resources allows you to reinforce your understanding and improve problem-solving skills. These resources offer additional practice, detailed explanations, and interactive methods to make learning more effective and engaging.

Study Materials and Platforms

Resource	Description	Access
Online Tutorials	Step-by-step video explanations of key concepts with visual aids.	Websites such as Khan Academy or YouTube.
Interactive Practice	Engage with quizzes and interactive problems that adapt to your level.	Educational websites like IXL or Mathway.
Textbooks	Traditional resources offering detailed explanations and exercises for each topic.	Available in libraries or through educational institutions.
Study Groups	Collaborative learning environments where you can discuss problems and solutions with peers.	Form groups locally or through online forums like Reddit or Discord.
Practice Worksheets	Printable worksheets that allow for hands-on practice with immediate feedback.	Websites offering free resources, such as Math-Drills.com.

How to Prepare for Algebra Tests

Effective preparation for mathematical assessments requires a strategic approach. By identifying key topics, organizing study sessions, and practicing regularly, you can boost your understanding and increase your confidence. Focused preparation helps you address weaknesses, reinforce strengths, and ensure you’re ready for any questions that may arise during the assessment.

Preparation Strategies

Strategy	Description	Example
Review Core Concepts	Focus on the most important topics that are likely to appear in the assessment.	Understand operations with fractions, solving for variables, and working with equations.
Practice Regularly	Engage with practice problems to apply what you’ve learned and improve your problem-solving skills.	Use practice worksheets or online exercises to simulate the actual experience.
Work Through Example Problems	Study worked-out examples to understand step-by-step processes and the reasoning behind each solution.	Look at sample problems and their solutions to understand the correct methodology.
Join Study Groups	Collaborate with peers to discuss challenging concepts and clarify doubts.	Form or join a study group to share insights and help each other.
Ask for Help	Don’t hesitate to seek assistance from teachers, tutors, or online resources when needed.	Use office hours, tutoring centers, or online forums for additional support.
Review Mistakes	Identify and learn from errors made in practice problems to avoid repeating them.	Go over incorrect answers and understand the reasoning behind the correct ones.

Tips for Mastering Algebra Concepts

Mastering mathematical principles requires a deep understanding of foundational concepts and consistent practice. By breaking down complex ideas into manageable steps, applying various problem-solving strategies, and reinforcing your knowledge regularly, you can enhance your ability to tackle even the most challenging problems. Below are some effective tips that can help you gain confidence and improve your skills.

Understand the Basics: Start with the fundamental rules and gradually build upon them. A solid grasp of basic operations lays the foundation for more advanced topics.
Practice Consistently: The more you practice, the more familiar you become with different problem types. Regular practice allows you to identify patterns and improve efficiency.
Focus on Problem-Solving Strategies: Learn and apply various methods to solve problems, such as simplifying expressions, using substitution, or factoring. This flexibility will help you approach problems from different angles.
Work on Word Problems: Translating real-world scenarios into mathematical expressions is a valuable skill. Practice converting word problems into equations to strengthen your reasoning and analytical abilities.
Use Visual Aids: Diagrams, graphs, and charts can help you visualize problems and understand relationships between variables. Drawing out problems can often make them easier to solve.
Break Down Complex Problems: When facing a difficult question, break it into smaller, more manageable parts. Solve each part step by step to avoid feeling overwhelmed.
Review and Reflect: After completing a problem, take time to review the steps you took. Reflect on any mistakes and learn from them to avoid repeating them in the future.
Ask for Help: If you’re stuck, don’t hesitate to reach out to a teacher, tutor, or online resource for guidance. Understanding where you went wrong is crucial for growth.

Strategies for Effective Test-Taking

Successfully navigating an academic assessment requires more than just understanding the material. Effective strategies can help you manage time, reduce anxiety, and maximize your performance. By approaching the exam with a clear plan, staying organized, and applying smart techniques during the process, you can increase your chances of achieving the best possible result.

Test Preparation Tips

Strategy	Description	Benefit
Review Key Concepts	Focus on the main topics and areas most likely to appear on the exam. Skim through your notes or textbooks to refresh your memory.	Prepares you with the most relevant material, improving efficiency and confidence.
Practice Under Timed Conditions	Simulate real exam conditions by timing yourself during practice sessions.	Helps you develop time-management skills and reduces stress during the actual exam.
Organize Your Materials	Ensure all the necessary materials (e.g., pencils, calculator, ID) are ready before the day of the assessment.	Reduces distractions and last-minute stress, helping you stay focused.
Get Enough Rest	Aim for a good night’s sleep before the exam day.	A well-rested mind performs better, improving concentration and recall.
Eat a Healthy Meal	Eat a balanced meal before the exam to keep your energy levels steady.	Maintains focus and cognitive function during the exam.

During the Exam

Strategy	Description	Benefit
Read All Instructions Carefully	Take time to read the instructions thoroughly before answering any questions.	Prevents mistakes from misinterpreting questions, ensuring you answer correctly.
Manage Your Time Wisely	Allocate time for each section based on its difficulty and point value. Don’t spend too much time on any one question.	Ensures that you complete the entire assessment and allows time for review.
Start with What You Know	Begin with questions you are confident about. This boosts your confidence and can help with time management.	Minimizes stress and maximizes early points.
Stay Calm and Focused	If you come across a difficult question, move on and come back to it later. Stay calm to keep your mind clear.	Helps reduce anxiety and prevents losing focus on easier questions.
Review Your Work	If time permits, review your answers before submitting the exam.	Allows you to catch any errors and make corrections if necessary.

Using Practice Tests to Improve Performance

Simulating the actual assessment environment through practice exercises is an effective way to boost your preparation and increase your chances of success. These mock assessments not only familiarize you with the structure and timing of the real exam but also help you identify areas that need improvement. By regularly engaging in practice drills, you can build confidence, enhance your problem-solving skills, and sharpen your test-taking strategies.

Practice assessments offer a valuable opportunity to assess your knowledge and refine your approach. By replicating the conditions of the real evaluation, you can improve your ability to manage time, understand question formats, and apply learned concepts in a practical setting. These exercises highlight your strengths and weaknesses, enabling you to focus your efforts on the areas that need the most attention.

Benefits of Practice Drills

Familiarization with Exam Format: Practice tests help you become accustomed to the question formats and the layout of the assessment, making the real test feel less overwhelming.
Time Management: Simulating time constraints helps you gauge how long to spend on each section, preventing you from spending too much time on difficult questions.
Identifying Weak Areas: Completing practice exercises allows you to pinpoint areas where your understanding is lacking and focus on improving those specific topics.
Building Confidence: Regularly practicing helps boost your self-confidence, reducing test anxiety and increasing your comfort level during the actual exam.
Improved Retention: Repeating questions in a practice setting helps reinforce concepts in your long-term memory, aiding recall during the assessment.

How to Maximize Practice Effectiveness

Take Timed Practices: Simulate real exam conditions by adhering to time limits for each practice session.
Review Mistakes: After completing a practice session, carefully review any incorrect answers and understand why you made those mistakes.
Use Multiple Resources: Take advantage of various practice tools, such as online platforms, textbooks, or past assessments, to ensure a wide range of questions.
Track Your Progress: Keep a record of your scores and note any recurring difficulties, allowing you to track improvement over time.
Mix Up the Question Types: Practice a variety of question formats to ensure you are well-prepared for all aspects of the real assessment.

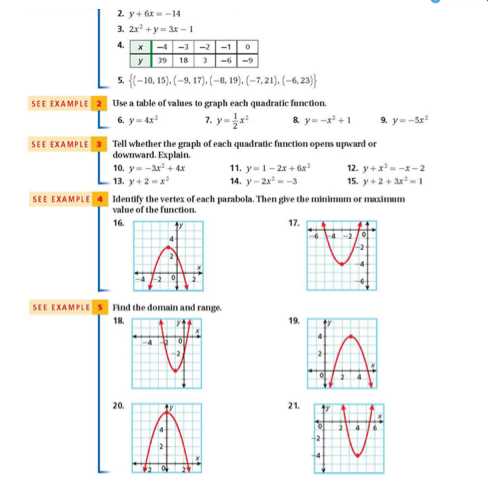
Understanding Equations and Functions

Equations and functions are foundational concepts in mathematics that help in expressing relationships between variables. An equation represents a statement of equality, where two expressions are set equal to each other, while a function defines a specific relationship between inputs and outputs. Understanding these concepts is essential for solving problems and analyzing patterns within various mathematical contexts.

When working with equations, the goal is often to find the value of an unknown variable that satisfies the equation. Functions, on the other hand, map one set of numbers to another, allowing us to understand how one variable changes in relation to another. Both concepts play a critical role in more advanced problem-solving and mathematical reasoning.

Key Characteristics of Equations

Equality: An equation involves an equals sign, indicating that the two sides of the equation are balanced or equivalent.
Variables: Equations often contain variables, which are placeholders for unknown values that need to be solved for.
Solving Equations: The process of solving an equation involves isolating the variable to determine its value.
Types of Equations: Equations can take many forms, including linear, quadratic, and exponential, each requiring different techniques for solving.

Understanding Functions

Input and Output: A function takes an input (often referred to as the independent variable) and produces an output (the dependent variable).
Notation: Functions are commonly written as f(x), where f represents the function and x is the input value.
Mapping: A function defines how each input value corresponds to exactly one output value, ensuring a consistent relationship.
Function Types: Functions can be linear, quadratic, or polynomial, each with different patterns and properties.

How to Manage Time During the Exam

Effectively managing time during an examination is crucial for success. It involves planning how to allocate time for each section or question while maintaining focus and reducing stress. Without a clear strategy, it’s easy to get caught up in difficult problems, which can leave little time for others. Time management ensures that all areas are addressed thoughtfully, giving you the best chance to perform well.

To manage time efficiently, it’s important to start by reviewing the entire exam and determining how long you should spend on each part. Avoid spending too much time on any single question. If a problem seems too complex, move on and return to it later with a fresh perspective. This approach helps in maximizing your overall performance and reduces the chance of running out of time.

Read Through the Entire Exam: Before starting, quickly skim through all the questions to get an overview and plan your approach.
Prioritize Easier Questions: Tackle the questions you find easier first. This will help build confidence and secure quick points.
Set Time Limits for Each Question: Allocate a specific amount of time for each question, and stick to it. This will prevent getting stuck on any one part of the exam.
Leave Difficult Questions for Later: If you encounter a difficult question, move on to others and come back to it with a clear mind.
Use Any Extra Time to Review: If you finish early, use the remaining time to check your answers and ensure everything is correct.

What to Do After Completing Section 1

After finishing the first part of the assessment, it’s important to take a moment to evaluate your work and ensure everything is in order. Rushing through the remaining tasks or proceeding without a final check may result in overlooked mistakes. This period is an opportunity to confirm that all sections have been addressed appropriately and that no steps have been missed.

Start by reviewing your responses carefully. Look for common errors such as skipped questions or misread instructions. If time allows, reread the most challenging questions to see if you can spot any overlooked details or better solutions. This step helps in boosting your overall score and minimizes the chances of errors that could have been easily corrected.

Check for Mistakes: Go through each response to spot any obvious errors. Pay attention to calculations, spelling, and the correct application of formulas.
Ensure All Questions Are Answered: Make sure no questions are left unanswered, especially if there are multiple parts within a single question.
Review Time Management: Double-check if you’ve allotted appropriate time to each question and if you still have time left for a final review.
Stay Calm and Focused: Avoid panicking if you feel unsure about any of your answers. A calm mind is essential for catching any mistakes and making the most out of your work.
Prepare for the Next Section: If your exam involves multiple parts, take a moment to prepare mentally for the next section, shifting focus from the completed portion.

How to Check Your Answers Carefully

After completing an assessment, it’s crucial to review your work meticulously before submitting it. This step ensures that you haven’t missed any details and that your responses are as accurate as possible. Checking your answers thoroughly can help you catch mistakes that you may have overlooked during the initial attempt.

Start by going over each question again, paying close attention to both the wording of the problem and your solution. It’s easy to make errors when in a rush, so a careful review helps you identify potential issues before it’s too late. Here are some effective strategies for reviewing your work:

Verify Your Calculations: Recheck all numerical work to ensure there are no calculation errors. Even small mistakes can change the outcome significantly.
Double-Check Your Work for Consistency: Make sure that the answers are consistent with the problem’s requirements. For instance, if the question asks for a positive number, ensure that your response reflects this.
Read the Instructions Again: Sometimes, you may have missed part of the instructions or misinterpreted them. Reread the question carefully to confirm that your response aligns with the instructions.
Look for Common Errors: Identify typical mistakes such as incorrect signs, misplaced decimal points, or overlooked variables. These types of errors are easy to make but can be avoided with careful attention.
Review Your Work in Chunks: Instead of reviewing the entire exam at once, break it down into smaller sections. This method allows you to focus on one part of the assessment at a time, making it easier to spot errors.

By following these tips, you can improve the accuracy of your responses and increase your chances of achieving a higher score. A well-organized and thorough review is one of the best ways to ensure your work is error-free.

Where to Find Additional Test Help

If you’re looking for extra assistance before an important assessment, there are several resources available to help you improve your skills and boost your confidence. These resources can provide clarity on difficult topics, offer practice materials, and help you strengthen your understanding of the material. Whether you’re studying independently or seeking guidance, knowing where to find support can make all the difference.

Here are some of the best places to look for additional help:

Online Learning Platforms: Numerous websites offer interactive lessons, practice exercises, and step-by-step tutorials. These platforms often allow you to study at your own pace, giving you the flexibility to focus on areas where you need the most improvement.
Tutoring Services: Whether in-person or online, a tutor can provide personalized guidance to address specific challenges. Tutors are often available through schools, educational centers, or online platforms. They can walk you through difficult concepts and answer any questions you may have.
Study Groups: Joining a study group with peers can provide additional perspectives and insights. Collaborative learning allows you to discuss topics in-depth, share resources, and help each other tackle difficult problems.
Teacher or Instructor Office Hours: Many instructors offer office hours or extra help sessions where you can ask questions and clarify any uncertainties you may have. Don’t hesitate to reach out to your teacher for additional support–they’re there to help you succeed.
Textbooks and Study Guides: Often, textbooks and supplementary materials have practice questions, explanations, and examples that can reinforce what you’ve learned. Be sure to thoroughly review the sections you find challenging, and use any study guides or answer keys provided to assess your understanding.
Educational YouTube Channels: YouTube is home to countless educational channels that break down complex topics into digestible videos. Searching for specific problems or concepts can yield detailed explanations and visual demonstrations, which can enhance your understanding.

By utilizing these resources, you can gain a deeper understanding of the material, reinforce your knowledge, and feel more confident when it’s time to face your assessment. Don’t hesitate to seek help whenever you feel stuck–there are plenty of options available to support your learning journey.

Reviewing Key Concepts for Success

When preparing for any evaluation in mathematical subjects, revisiting the foundational concepts is crucial for achieving success. By ensuring that you have a solid grasp of the core topics, you can approach problems with confidence and improve your overall performance. This section highlights some of the most important areas to focus on during your review, providing a structured approach to help you strengthen your understanding and maximize your results.

Core Areas to Focus On

Below are the fundamental topics that are frequently tested and essential for building a strong mathematical foundation:

Topic	Why It’s Important
Linear Equations	Understanding how to solve simple and complex linear equations is essential, as they form the basis for many other concepts and problem-solving strategies.
Polynomials	Mastery of polynomials allows you to simplify and solve expressions that appear in a wide variety of problems. Factoring and expanding polynomials are key skills.
Functions	Grasping the concept of functions and how to work with them enables you to solve a range of problems involving relationships between variables.
Systems of Equations	Being able to solve systems of equations–whether through substitution, elimination, or graphing–helps you tackle multi-variable problems effectively.
Inequalities	Understanding how to solve and graph inequalities is crucial for solving problems where values need to satisfy specific conditions.

Effective Strategies for Reviewing

Here are some strategies to help you maximize your review time and boost your understanding:

Practice Regularly: The more problems you work through, the more familiar you will become with the concepts and different types of questions. Practice helps to reinforce learning and build confidence.
Focus on Weak Areas: Identify the topics that challenge you the most and dedicate extra time to them. Make sure you understand the foundational principles before moving on to more complex topics.
Use Study Aids: Leverage textbooks, online resources, and practice exercises to supplement your understanding. Many platforms offer interactive tools and step-by-step guides that can help clarify difficult topics.
Review Mistakes: Pay attention to the errors you make while practicing. Understanding why a mistake occurred can help you avoid similar errors in the future.
Collaborate with Peers: Working with study partners can provide new perspectives and help you solve problems you might struggle with on your own. Collaborative learning can enhance comprehension.

By focusing on these essential topics and applying effective review strategies, you can deepen your understanding and improve your performance in any mathematical assessment. Make sure to prioritize these key concepts and practice consistently for the best results.