In this part of the curriculum, students explore essential topics that form the foundation for advanced problem-solving. The focus is on understanding complex relationships between numbers and applying different methods to find solutions. This section challenges learners to think critically and approach problems from multiple angles.
Through interactive exercises and detailed explanations, students can improve their ability to tackle difficult equations. By breaking down each problem into smaller, manageable steps, learners develop the skills needed to solve similar challenges in the future. Hands-on practice and gradual mastery are key to progressing in this area.
Whether you’re reviewing material or seeking to deepen your understanding, this part of the course provides all the necessary tools for success. The variety of exercises ensures that students can reinforce their knowledge while honing problem-solving techniques.
Algebra Nation Section 10 Answers Overview
This part of the learning material focuses on building a strong understanding of core mathematical principles. The exercises aim to develop a deeper insight into solving mathematical expressions and applying various strategies to reach solutions. Learners engage with progressively challenging problems that test their ability to think critically and methodically.
Key Concepts Covered
- Understanding fundamental operations and their interrelations.
- Breaking down complex equations into simpler forms.
- Using logical reasoning to solve step-by-step problems.
- Mastering the application of learned methods in real-world scenarios.
Benefits of this Learning Approach
- Improved problem-solving skills through guided practice.
- Clear explanations that enhance comprehension.
- Increased confidence in tackling difficult mathematical tasks.
- Ability to approach future challenges with a methodical mindset.
By completing these exercises, learners gain valuable experience in handling various mathematical challenges and can improve their overall proficiency in the subject. The focused practice ensures that each concept is thoroughly explored, providing students with the tools necessary for further academic success.
Understanding Algebra Nation Section 10
This part of the curriculum introduces a series of essential problems designed to strengthen your grasp of mathematical reasoning and solution strategies. It focuses on applying various techniques to solve complex equations and mathematical puzzles, providing a solid foundation for tackling more advanced topics. Each problem encourages critical thinking and systematic analysis.
Core Skills Developed
- Critical thinking: Analyzing problems from multiple perspectives.
- Step-by-step problem solving: Breaking down larger problems into manageable steps.
- Practical application: Using learned concepts in real-life scenarios.
Approaching the Exercises
The problems in this part require a mix of logical reasoning and mathematical techniques. By approaching each challenge methodically, you will be able to apply the correct principles and achieve the right solutions. Regular practice ensures that these skills become second nature, allowing for efficient problem solving in future tasks.
Key Concepts in Section 10
This part of the material emphasizes the application of fundamental mathematical principles to solve a variety of problems. It explores how different techniques can be used in tandem to simplify complex expressions and equations. Understanding these core ideas is crucial for progressing to more advanced topics and improving problem-solving efficiency.
Key topics covered include methods for simplifying mathematical expressions, techniques for solving multi-step problems, and the use of reasoning to identify patterns and relationships between numbers. Mastery of these concepts is essential for handling more challenging tasks in the future.
Solving Problems from Section 10
This section challenges learners to apply various techniques to solve complex problems. It involves breaking down intricate equations into simpler components, using logical reasoning to identify patterns, and selecting the appropriate methods to reach the correct solutions. Mastery of these skills is key to progressing in more advanced mathematical topics.
To illustrate the approach, consider the following example of a multi-step problem and its solution:
| Step | Action | Result |
|---|---|---|
| 1 | Identify the equation | 3x + 5 = 20 |
| 2 | Isolate the variable | 3x = 15 |
| 3 | Solve for x | x = 5 |
This simple example demonstrates how a problem can be broken down into manageable steps. By consistently following a clear, methodical process, learners can solve even the most challenging tasks with confidence and accuracy.
Step-by-Step Solutions for Section 10
This section is designed to guide learners through complex problems by breaking them down into simpler, more manageable steps. Each problem is approached methodically, allowing students to follow a logical progression from start to finish. This step-by-step approach helps ensure that key concepts are understood and can be applied correctly in future challenges.
By following these detailed instructions, learners can learn how to isolate variables, simplify expressions, and solve multi-step equations with ease. Consistency in following the steps is crucial for developing a strong problem-solving foundation and improving accuracy when handling more difficult tasks.
The process emphasizes clarity and organization, ensuring that each step builds upon the previous one. By practicing this structured approach, students gain confidence in their ability to tackle a wide range of mathematical problems.
Common Mistakes in Algebra Section 10
When tackling mathematical challenges, it’s easy to make simple errors that can lead to incorrect results. These mistakes often stem from misunderstandings of key concepts or overlooking important steps in the problem-solving process. Recognizing and avoiding these common errors is essential for improving both accuracy and efficiency.
Common Errors to Avoid

- Skipping steps: Rushing through problems and skipping important steps can result in missing key details and lead to incorrect answers.
- Incorrect simplification: Failing to properly simplify expressions before solving can make the problem more difficult than necessary.
- Sign mistakes: Neglecting the correct handling of positive and negative signs during calculations is a frequent issue.
- Misapplication of formulas: Using the wrong method for a specific problem type can cause confusion and errors in the final result.
How to Avoid These Pitfalls
Paying attention to every detail and ensuring that each step is followed methodically will significantly reduce the risk of making mistakes. Slow and careful work is often more effective than rushing through problems without fully understanding the process.
Tips for Mastering Section 10
To succeed in this part of the course, it’s important to approach each problem with a clear strategy. Mastering the material requires more than just solving problems; it involves understanding the underlying concepts and consistently applying the right techniques. Here are some effective tips to help you achieve mastery.
Effective Study Habits
- Practice regularly: Consistent practice helps reinforce key concepts and improve problem-solving speed.
- Review mistakes: Analyze errors to understand where you went wrong and avoid repeating the same mistakes.
- Break down complex problems: Divide larger problems into smaller, manageable steps for better focus and accuracy.
Approach to Learning
- Focus on understanding: Strive to grasp the “why” behind each method, not just the “how.”
- Use visual aids: Draw diagrams or use charts to visualize problems and simplify complex ideas.
- Stay patient: Take your time with difficult problems and give yourself room to think through each step carefully.
By following these strategies, you’ll not only improve your ability to solve problems but also deepen your understanding of the concepts that form the foundation of this material.
Real-World Applications of Section 10
The concepts explored in this part of the course are not just academic–they have practical applications in everyday life. From managing finances to solving engineering problems, the skills developed here are essential for making informed decisions and solving real-world issues. Understanding how to apply mathematical techniques can open doors to various professional fields and improve decision-making in various contexts.
Practical Uses in Daily Life
- Budgeting and Personal Finance: Understanding how to solve equations helps in managing expenses, savings, and investments.
- Construction and Engineering: Solving complex calculations is key for building structures, determining materials, and estimating costs.
- Data Analysis: Mathematical skills are used to analyze trends, make predictions, and interpret data in fields such as marketing and economics.
Professional Applications
- Technology and Software Development: Coding and programming rely heavily on understanding algorithms and solving mathematical problems.
- Science and Research: In fields such as physics and biology, mathematical modeling is used to predict outcomes and solve research problems.
- Medicine: Medical professionals use calculations to determine proper dosages, interpret test results, and analyze health data.
By mastering the principles covered in this part of the curriculum, learners gain valuable skills that are highly applicable across many industries and can lead to more effective problem-solving in both professional and personal contexts.
Practice Questions for Section 10
To fully grasp the concepts covered in this part of the course, consistent practice is essential. The following set of practice problems will help reinforce key ideas and improve problem-solving skills. By solving these exercises, learners can apply what they’ve learned and deepen their understanding of the material.
| Problem | Solution Steps |
|---|---|
| Solve for x: 4x + 7 = 19 | 1. Subtract 7 from both sides. 2. Divide both sides by 4. |
| Simplify the expression: 3(2x + 5) – 4x | 1. Distribute the 3 to both terms inside the parentheses. 2. Combine like terms. |
| Find the value of y: 2y – 5 = 3y + 4 | 1. Move all terms involving y to one side. 2. Solve for y by isolating it. |
| Factor the expression: x^2 + 5x + 6 | 1. Find two numbers that multiply to 6 and add to 5. 2. Write the factored form. |
These problems cover a variety of techniques and encourage a deeper understanding of the material. By practicing regularly, you can improve your ability to solve problems accurately and efficiently.
Interactive Features in Algebra Nation
The platform offers various interactive tools designed to enhance learning and engagement. These features allow students to actively participate in their education, solve problems in real-time, and receive immediate feedback. By using these tools, learners can reinforce their understanding of key concepts and track their progress effectively.
Engaging Tools for Learning
Interactive elements such as quizzes, practice exercises, and real-time problem-solving simulations provide students with the opportunity to apply what they’ve learned. These tools make learning more dynamic and help to cement the theoretical knowledge through hands-on practice.
Features Overview
| Feature | Description |
|---|---|
| Instant Feedback | Get immediate results and explanations after completing problems to help reinforce learning. |
| Progress Tracker | Monitor your performance over time and identify areas that need improvement. |
| Interactive Exercises | Complete interactive tasks that challenge your understanding and provide step-by-step solutions. |
| Discussion Forums | Engage with peers and instructors to discuss solutions and clarify doubts. |
These features help create an interactive learning experience that keeps students motivated and involved in the process. Whether practicing independently or collaborating with others, these tools are designed to build confidence and improve problem-solving skills.
Section 10 Answer Keys Explained
Answer keys provide detailed solutions and explanations for exercises, enabling students to understand not only the correct answers but also the step-by-step processes used to arrive at those solutions. These resources are essential for reinforcing learning and clarifying concepts that may be difficult at first glance. By reviewing these keys, students can gain a deeper understanding of the problem-solving methods and improve their ability to tackle similar problems in the future.
How Answer Keys Enhance Learning
Answer keys are more than just a final solution; they are a valuable learning tool that breaks down each problem into its components. By following the steps provided, learners can see how to approach similar questions, avoid common mistakes, and develop a more structured thought process. Additionally, answer keys offer insights into different problem-solving strategies, providing a broader understanding of mathematical methods.
Overview of Key Features
| Feature | Description |
|---|---|
| Step-by-step breakdown | Each solution is divided into clear steps to guide students through the reasoning process. |
| Common Mistakes | Highlighted common errors help students recognize where they might go wrong and how to avoid it. |
| Alternative Methods | Different approaches to solving a problem are presented, offering students multiple ways to understand the concept. |
| Tips and Tricks | Helpful hints throughout the key assist in simplifying difficult problems and speeding up calculations. |
Reviewing the answer keys thoroughly not only strengthens comprehension but also builds confidence in solving future problems. These detailed solutions help foster independence in learning and prepare students for more complex challenges ahead.
How to Use Algebra Nation Effectively
To get the most out of the platform, it’s important to engage with all of its features actively and consistently. The interactive tools and resources available are designed to support learning by providing hands-on practice, real-time feedback, and clear explanations. Understanding how to navigate and utilize these resources can significantly enhance your understanding of the material and help you achieve better results.
Start with a Clear Goal
Before diving into the exercises, take a moment to assess your goals. Whether you’re reviewing concepts you’ve already learned or tackling new topics, having a clear objective helps you stay focused. Knowing what you want to achieve will allow you to target specific areas for improvement and make your study sessions more productive.
Utilize Practice Tools
Make sure to regularly complete practice exercises. These tools help reinforce what you’ve learned by providing a variety of problems to solve. Be sure to take advantage of the instant feedback feature, which gives you immediate insight into your progress and areas where you might need more practice.
Review Solutions Thoroughly
Don’t just look at the correct answers–take the time to review the detailed solutions provided. Going through the step-by-step breakdowns will help you understand the reasoning behind each solution, allowing you to apply similar strategies to different problems. This practice is key to mastering the material and improving your problem-solving skills.
Track Your Progress
Monitor your development using the platform’s progress tracking features. By regularly checking your results, you can identify areas of strength and weaknesses, which allows you to focus your study time more effectively. Setting personal milestones and measuring improvement over time will keep you motivated and on track.
Engage with the Community
Don’t hesitate to reach out for help when needed. Many platforms provide forums or discussion boards where you can ask questions and collaborate with peers or instructors. Engaging with the community can provide valuable perspectives, solutions to challenges, and encouragement along the way.
By approaching the platform strategically and utilizing these tips, you can maximize your learning experience and see significant improvements in your understanding of the material.
Strategies for Section 10 Success
Achieving success in any area of study requires more than just passive learning–it demands a structured approach, active practice, and the ability to analyze mistakes. In this section, we’ll explore effective strategies that can help you navigate challenges and improve your performance. By adopting these techniques, you’ll be able to tackle complex problems with confidence and mastery.
Focus on Key Concepts
Understanding the core concepts is essential to solving any problem. Rather than memorizing formulas or methods, aim to grasp the underlying principles that drive each solution. This deeper understanding will allow you to apply what you’ve learned to a variety of situations, making you more adaptable to different types of questions. Review the fundamentals regularly to ensure they remain fresh in your mind.
Break Down Problems Step-by-Step
One of the most effective ways to approach challenging exercises is by breaking them down into smaller, more manageable parts. Start with the simplest components of the problem, and then gradually build up to more complex steps. This method helps to reduce overwhelm and ensures that you address each part systematically, preventing careless mistakes. Take your time and ensure that each step is understood before moving on to the next.
Remember that practice is key to improvement. As you work through problems and apply these strategies, you will naturally build greater confidence in your ability to handle more difficult tasks. Keep reviewing, stay consistent, and you’ll see continued progress over time.
Breaking Down Complex Problems
When faced with challenging tasks, it’s important to approach them methodically rather than trying to solve everything at once. Breaking down complex problems into smaller, more manageable steps helps reduce confusion and makes it easier to focus on the essential parts. By following a structured approach, you can tackle even the most difficult questions with greater efficiency and confidence.
Identify the Core Components
The first step in simplifying a difficult problem is to identify its core elements. What is the main question? What information do you already have, and what do you need to find out? By understanding the problem’s fundamental structure, you can create a roadmap that will guide your approach. Focus on the key parts and set aside any distractions.
Break It Into Logical Steps
Once you’ve identified the main components, start breaking the problem down into smaller, logical steps. This allows you to solve each part independently before piecing the overall solution together. For example, if you’re solving a multi-step equation, focus on one operation at a time rather than trying to handle everything in one go. By simplifying each part of the problem, you’ll ensure that no steps are overlooked.
Work Backwards if Necessary
If a problem seems especially tricky, sometimes working backwards can be helpful. Start with the end result and consider the steps that would lead to that outcome. This strategy can often reveal shortcuts or alternative methods that you might not have thought of initially.
Approaching complex tasks with a clear and methodical process not only makes problem-solving more manageable but also enhances your overall understanding of the material. By breaking problems down into smaller, logical steps, you’ll develop stronger skills and gain the confidence needed to handle even more challenging problems in the future.
Frequently Asked Questions About Section 10
When working through complex topics, students often have similar questions regarding the material and how to approach it effectively. This section addresses some of the most commonly asked queries to help clarify any confusion and provide useful insights for better understanding and solving the problems at hand. Whether you’re just starting or reviewing the material, these answers can guide you toward mastering the concepts.
1. How do I approach challenging problems in this section?
When encountering difficult problems, it’s essential to break them down into smaller, more manageable steps. Identify the key components of the question, understand the underlying principles, and tackle each step one at a time. If needed, review related concepts to reinforce your understanding.
2. Are there any shortcuts to solving the problems more efficiently?
While there are no one-size-fits-all shortcuts, practicing different strategies like working backwards or identifying patterns can often lead to faster solutions. Additionally, mastering fundamental principles and techniques will help you recognize common approaches to similar problems.
3. What should I do if I don’t understand a specific concept?
If a concept is unclear, review the related examples and practice problems. Often, seeing a concept applied in different scenarios can help deepen your understanding. Don’t hesitate to ask for help, whether from peers, teachers, or online resources, as discussing and explaining the material can also aid comprehension.
4. How can I stay organized when solving problems in this area?
Staying organized is key to solving problems efficiently. Write down each step of your solution and double-check your work as you go. Keep a notebook or digital document with notes and formulas handy to refer back to as needed. Organization helps reduce errors and ensures that you don’t miss any important steps in your reasoning.
5. How can I test my understanding?
One of the best ways to test your understanding is to practice regularly. Solve additional problems outside of the ones you’re currently working on. If you’re able to apply the concepts successfully to a variety of problems, it indicates that you have a solid grasp of the material. Additionally, reviewing solutions and understanding mistakes can further strengthen your knowledge.
Additional Resources for Section 10
For those looking to deepen their understanding of the material and refine their problem-solving skills, there are several valuable resources available. These tools can help clarify complex concepts, provide extra practice, and offer different perspectives on the topics covered. Below are some of the most helpful resources you can explore to enhance your learning experience.
Online Tutorials and Video Lessons
Video tutorials are a great way to visually learn and understand challenging concepts. Many platforms offer step-by-step lessons that break down topics in an easy-to-understand manner.
- Khan Academy – Free lessons on a wide range of mathematical topics, with interactive exercises.
- YouTube – Channels dedicated to math tutorials, providing visual explanations and problem-solving strategies.
- Coursera – Offers paid and free courses from universities, focusing on problem-solving and practical applications.
Books and Study Guides
Books and study guides are excellent for a more in-depth review. Many publications provide practice problems with solutions and explanations that allow for thorough self-study.
- Amazon – Search for textbooks and workbooks designed specifically for mastering key concepts.
- Scholastic – Offers study guides that cover various levels of mathematical understanding.
- McGraw-Hill Education – Well-known for producing comprehensive textbooks and workbooks on various subjects, including mathematics.
Practice Problem Websites
Practicing problems from different sources can solidify your knowledge and prepare you for assessments. Here are some websites that provide an extensive collection of problems to help you get more hands-on experience.
- Wolfram Alpha – A powerful computational engine that allows you to solve problems step-by-step, showing detailed solutions.
- Brilliant – Interactive problems and puzzles that encourage critical thinking and problem-solving skills.
- SplashLearn – A website with practice exercises for a range of mathematical topics and interactive games to make learning fun.
Discussion Forums and Study Groups
If you prefer collaborative learning, joining discussion forums or study groups can be incredibly beneficial. You can share ideas, ask questions, and get help with challenging problems from others who are also learning.
- Reddit – Math Help – A forum where students and educators share insights, tips, and solutions to math problems.
- Khan Academy Community – A space where you can ask questions, discuss topics, and interact with other learners.
- StudyBlue – A platform for creating flashcards, reviewing study material, and connecting with peers for collaborative study.
By utilizing these resources, you can gain a deeper understanding of the topics covered, improve your problem-solving skills, and boost your confidence when working through mathematical challenges.
How to Improve Mathematical Skills
Improving your problem-solving abilities and mastering mathematical concepts requires consistent practice, understanding key principles, and applying them in different contexts. With the right approach, anyone can enhance their skills and gain confidence when tackling complex problems. Here are several effective strategies to help you make steady progress.
1. Practice Regularly
Repetition is one of the most effective ways to solidify your understanding and improve your skills. The more you practice, the more comfortable you become with various techniques and problem types.
- Work on practice problems daily to reinforce your understanding.
- Start with simpler problems and gradually increase the difficulty level.
- Use online platforms and worksheets to access a variety of problems.
2. Understand Key Concepts
Simply memorizing formulas is not enough. It’s essential to understand the underlying principles and reasoning behind each concept. This will help you apply your knowledge more effectively in different scenarios.
- Break down each problem into smaller, manageable steps.
- Ask yourself why certain methods work and explore alternative approaches.
- Take time to review mistakes and understand where you went wrong.
3. Seek Help When Needed
If you’re struggling with a particular topic, don’t hesitate to ask for help. Working with others or seeking guidance from experienced individuals can provide new insights and speed up your progress.
- Join study groups where you can collaborate with peers and discuss challenging topics.
- Utilize online tutorials, video lessons, and resources to get additional explanations.
- Consult teachers, tutors, or mentors for personalized assistance.
4. Stay Consistent and Patient

Improvement takes time, and it’s important to stay patient and persistent. Consistency in your practice and dedication to mastering each concept will lead to gradual progress over time.
- Set achievable goals and track your progress regularly.
- Break down your study sessions into focused, manageable chunks.
- Celebrate small victories along the way to stay motivated.
By following these strategies, you’ll gradually build a strong foundation in mathematics and develop the skills needed to approach even the most challenging problems with confidence.
Preparing for Tests with Section 10
Effective preparation for assessments involves more than just reviewing notes or textbooks. It requires a strategic approach that includes practicing problems, understanding core principles, and utilizing resources to reinforce knowledge. The key to success is staying organized and methodical, ensuring that you are ready to tackle any challenge that might appear on the test.
1. Review Key Concepts Thoroughly

Before diving into practice problems, take time to review the most important concepts covered in the material. Ensure you understand the theory and the logic behind each principle, as this will help you solve problems more efficiently during the test.
- Summarize the main concepts and key points in your own words.
- Create a list of formulas or steps you need to remember, and refer to it frequently.
- Use flashcards or notes for quick revision of essential ideas and definitions.
2. Practice Problem Solving
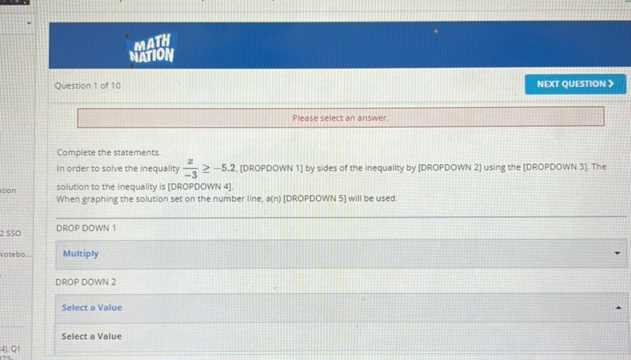
Solving problems is one of the best ways to prepare for any assessment. Practice with a variety of problems to ensure that you can apply concepts to different types of questions. This will help you become more comfortable and confident when it’s time to take the test.
- Start with easy problems to warm up, then progressively challenge yourself with harder ones.
- Use sample tests, practice sheets, or online platforms for additional problem sets.
- Track your mistakes and learn from them to avoid similar errors in the future.
3. Time Management and Practice Under Test Conditions
Being able to manage your time effectively during the test is crucial. Simulate real exam conditions by practicing with a timer. This will help you get accustomed to working under pressure and prevent any last-minute panic during the actual test.
- Set a timer for each practice session to mimic the time limits of the exam.
- Focus on completing problems efficiently without sacrificing accuracy.
- Review your work within the time constraints to ensure you’re staying on track.
4. Seek Help When Needed
If you encounter concepts or problems that are difficult to grasp, don’t hesitate to ask for help. Working with others or seeking expert guidance can provide clarity and improve your understanding.
- Consult with teachers or tutors to clarify confusing topics.
- Join study groups to collaborate and learn from peers.
- Use online resources, such as video tutorials or forums, to gain different perspectives on tricky concepts.
By incorporating these strategies into your study routine, you can maximize your preparation and approach the test with confidence and readiness.