In this guide, we focus on one of the most crucial parts of your mathematical journey, where understanding core principles can significantly boost your performance. Whether you’re preparing for an academic challenge or aiming to strengthen your foundation, grasping the fundamentals is essential for success. This section will help you tackle a variety of problems and build confidence in applying the right strategies.
Comprehending core techniques is the key to solving complex problems quickly and accurately. You’ll learn how to break down complicated expressions and use logical steps to navigate through them. By practicing and mastering these steps, you’ll gain the tools to approach any challenge with ease.
Reviewing solutions thoroughly can reveal hidden patterns and shortcuts, saving you time and effort. This methodical approach not only ensures accuracy but also sharpens your problem-solving abilities. With the right preparation, you’ll be ready to face any mathematical challenge head-on and achieve success.
Algebra Nation Section 2 Test Answers
In this section, the focus is on refining your understanding of core mathematical principles. The goal is to develop strong problem-solving skills and the ability to apply logical reasoning to a wide range of challenges. Mastering the concepts presented will give you the confidence to approach any problem methodically and with precision.
Building Strong Problem-Solving Strategies
Success in this area is all about mastering the necessary techniques. By recognizing patterns and applying proven methods, you can simplify complex expressions and arrive at solutions more efficiently. Practicing consistently will allow you to approach each question systematically, reducing the likelihood of errors.
Effective Review Techniques for Improved Performance
Once you have a strong grasp on the concepts, the next step is to review your work carefully. This will not only reinforce your knowledge but also help identify areas that may need further improvement. Effective review strategies include revisiting challenging problems and breaking them down into smaller, manageable steps.
Overview of Section 2 Test Format
This portion of the exam is designed to assess your understanding of key mathematical concepts and your ability to apply them in various scenarios. The format is structured to test both your knowledge and problem-solving skills through a series of carefully crafted questions. You will encounter a variety of question types that require different approaches, ranging from simple calculations to more complex reasoning tasks.
To better understand the structure, here’s a breakdown of how the questions are typically organized:
| Question Type | Skills Tested | Time Allocation |
|---|---|---|
| Multiple Choice | Concept recall and basic application | Short time |
| Fill-in-the-Blank | Understanding of key formulas | Medium time |
| Problem Solving | Logical reasoning and process application | Longer time |
By familiarizing yourself with this structure, you can improve your ability to navigate the questions efficiently and manage your time effectively. Each question type demands a slightly different approach, but understanding the format will help you tackle them confidently and with precision.
Key Concepts Covered in Section 2
This part of the examination emphasizes essential principles that form the foundation for solving various mathematical problems. The focus is on building a solid understanding of the underlying concepts, allowing you to approach each problem with a logical and methodical mindset. By mastering these core ideas, you can confidently tackle more complex challenges and apply them in different contexts.
The topics covered include fundamental operations, problem-solving strategies, and analytical techniques. You will encounter exercises that test your ability to manipulate expressions, work with different types of equations, and interpret mathematical relationships. Understanding these concepts is key to progressing through the more advanced material in future sections.
Tips for Mastering Algebra Nation
To excel in this area, it’s essential to develop a deep understanding of the core principles and consistently apply them. Success comes from not only memorizing formulas but also mastering the methods and strategies that make problem-solving efficient and effective. With the right approach, you can tackle even the most complex challenges with confidence and precision.
One key to mastery is regular practice. Consistently working through exercises allows you to become familiar with different problem types and refine your skills over time. Additionally, breaking down each problem into manageable steps helps avoid mistakes and ensures a structured approach. It’s also important to stay focused on the underlying concepts, as they provide the foundation for solving a wide variety of problems.
How to Approach Test Questions Effectively
When faced with challenging problems, it’s crucial to have a clear strategy that allows you to approach each question methodically. By staying organized and following a systematic approach, you can minimize errors and maximize efficiency. The key is to break down the problem into smaller steps, ensuring you fully understand what is being asked before jumping to a solution.
Step-by-Step Problem Solving
Start by identifying the key components of the question. Look for important details, such as given values, operations, and what you need to find. Organize the information clearly, and then think about which methods or formulas you can apply to move forward. Taking the time to analyze the problem first will help you avoid rushing into a solution that might lead to mistakes.
Time Management and Prioritization
Effective time management is just as important as problem-solving skills. It’s crucial to allocate enough time for each question without getting stuck on any single one for too long. If a question feels difficult, consider moving on and returning to it later with a fresh perspective. Prioritize questions that you can solve quickly to gain confidence before tackling the more complex ones.
| Approach | Key Focus | Time Allocation |
|---|---|---|
| Initial Scan | Identify key information and what is asked | 1-2 minutes |
| Methodical Breakdown | Use logical steps to solve | 3-5 minutes |
| Review and Check | Double-check work for errors | 2 minutes |
By following this approach, you’ll improve your ability to solve problems accurately and efficiently. Mastering these techniques will not only help you perform well but also develop lasting problem-solving skills that will serve you beyond the test.
Understanding Algebraic Expressions and Equations
At the heart of mathematical problem-solving lies the ability to understand and manipulate expressions and relationships between numbers and variables. These fundamental concepts are crucial for solving more complex problems and form the foundation of many advanced topics. By mastering how to interpret and work with these forms, you’ll gain the skills necessary to approach a wide range of challenges effectively.
Expressions consist of numbers, variables, and operations combined in various ways. Learning to identify and simplify these components is essential for solving equations and deriving solutions. It’s important to focus on understanding how each part of an expression interacts with others and how to simplify them step by step.
Equations, on the other hand, represent relationships between two or more expressions. Solving an equation often involves finding the value of a variable that satisfies the equality. By practicing different types of equations, you’ll develop the ability to choose the right methods to isolate variables and determine their values accurately.
Common Mistakes in Algebra Nation Tests
In any mathematical evaluation, it’s easy to make mistakes that can cost you valuable points. Understanding the common errors made during problem-solving is key to improving accuracy and boosting performance. Recognizing where mistakes tend to occur allows you to focus on those areas during preparation, leading to a more efficient and effective approach to the questions.
Frequent Errors During Problem Solving
Many students make similar mistakes when attempting to solve complex problems. These errors can stem from misreading the question, skipping critical steps, or rushing through calculations. Some of the most common mistakes include:
- Misinterpreting the question’s requirements
- Forgetting to apply the correct order of operations
- Making simple arithmetic errors under time pressure
- Overcomplicating simple problems by missing obvious solutions
- Neglecting to check the final answer for accuracy
How to Avoid These Mistakes
To minimize these common errors, it’s essential to adopt a methodical approach when tackling each question. Here are some strategies to avoid mistakes:
- Read each problem carefully to fully understand what is being asked before starting the solution process.
- Double-check the application of formulas and operations at each step.
- Practice solving problems under timed conditions to build speed without sacrificing accuracy.
- Take time to review the final answer and ensure it logically fits the context of the question.
- Ask for help or clarification if any part of the question seems unclear or confusing.
By staying mindful of these common pitfalls and applying the strategies above, you’ll reduce the likelihood of errors and increase your overall performance.
How to Use Practice Tests to Prepare
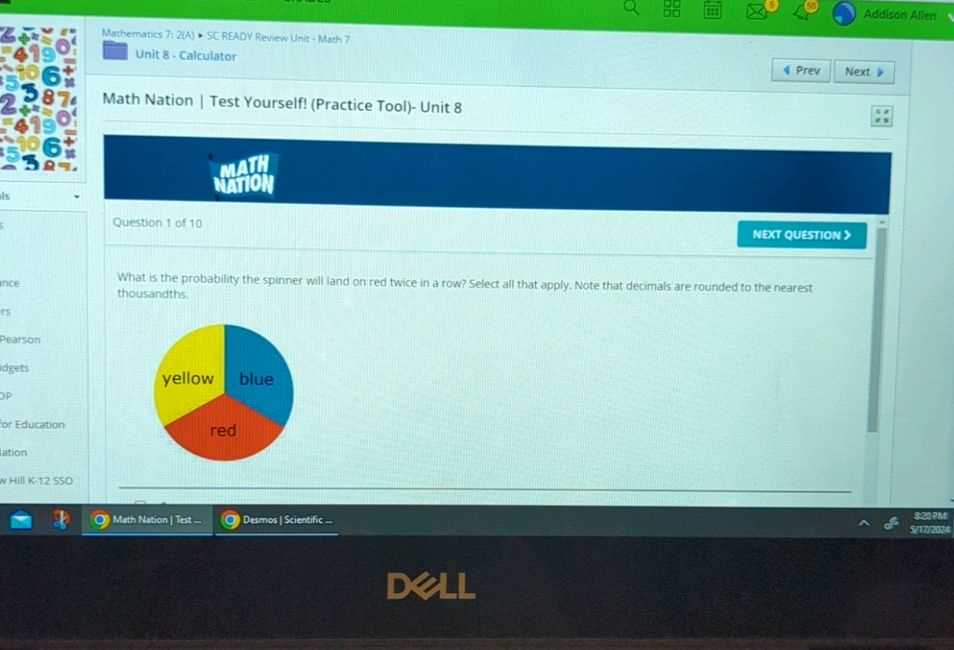
Using practice exams is an effective way to assess your readiness and identify areas where you may need additional focus. By simulating the actual testing experience, practice tests help you become familiar with the format, manage your time better, and reduce anxiety. These exercises provide valuable insights into your strengths and weaknesses, allowing you to adjust your study strategy accordingly.
Benefits of Practice Exercises
Taking practice questions is a key element of effective preparation. These exercises offer several advantages:
- Familiarity with question formats and structures
- Identification of common problem types and patterns
- Improved time management and pacing during assessments
- Increased confidence and reduced stress levels
How to Maximize the Effectiveness of Practice Tests
To get the most out of your practice sessions, follow these tips:
- Take full-length practice exams under timed conditions to simulate the real experience.
- Review your mistakes thoroughly and understand where you went wrong.
- Focus on weak areas by practicing similar problems multiple times.
- Track your progress to see how your skills improve over time.
- Use practice exams as a tool to refine your problem-solving strategies.
By incorporating these strategies into your study routine, you’ll be able to approach the actual exam with greater confidence and skill.
Time Management for Algebra Section 2
Effective time management is a crucial skill when preparing for any mathematical assessment. It allows you to allocate sufficient time for each problem while ensuring you don’t rush through important steps. Proper time allocation helps you avoid stress, make thoughtful decisions, and complete the evaluation with accuracy and confidence.
Planning Your Approach
Before diving into the problems, it’s essential to plan how you’ll approach the entire process. Consider how long you should spend on each question and set time limits for each section. A well-structured plan ensures that you don’t get stuck on difficult questions, allowing you to move through the problems efficiently.
Strategies for Staying on Track
To manage time effectively during the assessment, keep these tips in mind:
- Prioritize Simple Questions: Start with problems you can solve quickly to gain confidence and momentum.
- Set Time Limits: Allocate specific time for each question. If you’re stuck, move on and return to it later.
- Monitor Your Progress: Periodically check the time to ensure you’re on track. Adjust your pace as needed.
- Don’t Overthink: Trust your preparation and avoid spending too much time on any one problem.
By using these strategies, you’ll ensure that you stay focused and efficient throughout the assessment, maximizing your performance.
Breaking Down Complex Algebra Problems
When faced with a challenging mathematical problem, the key to finding the solution is breaking it down into smaller, more manageable steps. This approach helps to simplify complex relationships and makes it easier to focus on solving each part methodically. Instead of feeling overwhelmed, understanding how to deconstruct a problem allows you to tackle it logically and systematically.
Identifying Key Components
The first step in simplifying a problem is to identify its essential elements. Look for known values, variables, and operations that need to be applied. By separating the core components, you can begin to create a roadmap for solving the problem.
Step-by-Step Problem Solving
Once you’ve broken down the problem, follow a structured approach to solve it. Here’s how you can approach each step:
- Read Carefully: Understand the problem by reading it thoroughly before starting any calculations.
- Simplify: Look for ways to simplify expressions or eliminate unnecessary terms.
- Apply Operations Sequentially: Solve the problem step by step, ensuring each operation is completed before moving to the next.
- Check Your Work: After solving, review each step to confirm that everything is accurate.
By breaking down complex problems in this way, you can reduce confusion and ensure a clear path to the solution. This method also builds your confidence in solving more difficult questions with ease.
Utilizing Online Resources for Practice
In today’s digital age, the internet offers a wealth of resources that can significantly enhance your preparation for any mathematical assessment. Online platforms provide interactive exercises, detailed tutorials, and practice materials that are accessible anytime. Leveraging these tools can help you reinforce your understanding and improve your problem-solving skills.
Benefits of Using Online Tools
Online resources offer several advantages that traditional study methods may not provide:
- Immediate Feedback: Many platforms give instant feedback on your answers, helping you identify mistakes and learn from them right away.
- Variety of Problems: You can access a wide range of practice questions covering different topics and difficulty levels.
- Interactive Learning: Visual aids, videos, and simulations help you grasp complex concepts in an engaging way.
- Flexible Schedule: You can practice at your own pace, fitting it into your routine whenever it’s convenient.
Top Online Resources for Practice
Here are some of the best platforms that offer valuable practice materials:
- Khan Academy: Offers step-by-step lessons and practice exercises on a variety of topics.
- Wolfram Alpha: A powerful tool for solving complex problems and visualizing solutions.
- IXL: Provides personalized practice with detailed explanations for every answer.
- Coursera: Online courses that cover fundamental concepts with expert-led instruction.
By integrating these online resources into your study routine, you can boost your skills, track your progress, and approach challenges with more confidence.
Step-by-Step Solutions for Test Questions
When tackling mathematical problems, a step-by-step approach is essential to ensure accuracy and clarity. By breaking down complex problems into smaller, manageable parts, you can solve them efficiently and with confidence. This method allows you to focus on each step without feeling overwhelmed, ultimately leading to better performance and fewer mistakes.
Approach to Solving Problems
Here’s how you can approach each problem in a logical and methodical way:
- Read the Problem Thoroughly: Carefully analyze the question to understand what is being asked before you start solving.
- Identify Known and Unknown Values: Write down any given values and identify the unknowns you need to solve for.
- Set Up Equations: Translate the problem into equations that can be solved using known mathematical principles.
- Solve Step by Step: Work through each equation step by step, simplifying as you go, ensuring you don’t skip any steps.
- Verify Your Solution: Double-check your final answer by plugging it back into the original equation to ensure its accuracy.
Example Problem Breakdown
Below is an example of how to break down a typical problem:
| Step | Description | Result |
|---|---|---|
| 1 | Read and understand the question | Identify the variables and the relationship between them |
| 2 | Write the equation | Set up the correct equation based on the given information |
| 3 | Solve the equation | Use algebraic methods to isolate the variable |
| 4 | Check the solution | Substitute the solution back into the original equation to verify |
By following this systematic approach, you can break down even the most difficult problems into easy-to-handle steps, improving your efficiency and accuracy in solving them.
What to Do if You’re Stuck
Encountering difficulties while solving mathematical problems is common, but it doesn’t mean you’re failing. When you’re stuck, it’s important to remain calm and use a systematic approach to find a way forward. Instead of rushing through, take a step back, review your approach, and explore different strategies to overcome the challenge.
Strategies to Overcome Roadblocks
If you’re finding yourself at an impasse, here are some effective steps you can take to get back on track:
- Take a Break: Sometimes, stepping away for a moment can give you a fresh perspective when you return to the problem.
- Review the Problem: Reread the question carefully. Double-check for any details you might have missed or misunderstood.
- Work Backwards: If possible, start from the result you expect and work your way back to see if the calculations or assumptions hold.
- Seek Help: Don’t hesitate to ask for guidance from a peer, tutor, or instructor if you’re stuck on a particular concept.
- Use Resources: Online tutorials, videos, or step-by-step examples can help clarify complex topics or methods.
Common Pitfalls to Avoid
When you’re stuck, it’s easy to make hasty decisions or overlook key details. To avoid these common mistakes:
- Rushing Through: Avoid trying to quickly solve the problem without thinking it through. This often leads to more confusion.
- Skipping Steps: Ensure that you go through every step methodically instead of skipping ahead, as missing a key step can throw off your entire solution.
- Overcomplicating: Sometimes the simplest solution is the right one. Don’t overcomplicate things by making the problem harder than it is.
By using these strategies and avoiding common mistakes, you can confidently work through challenges and continue making progress. Stay persistent, and remember that each mistake is an opportunity to learn and improve.
Understanding Graphing and Functions
Mastering the representation of mathematical relationships visually is crucial for understanding how variables interact. Graphing allows us to translate abstract equations into clear, interpretable visuals, while functions provide the underlying rules that govern these relationships. By learning how to plot and analyze graphs, you can gain deeper insights into the behavior of different expressions and make better decisions based on their patterns.
The Basics of Graphing
When graphing equations, the goal is to plot points on a coordinate plane that satisfy the equation. Each point represents a solution, and by connecting these points, you can see the overall pattern or trend. Understanding the axes, scales, and how to interpret the graph’s shape is essential for making sense of what it represents.
- X-Axis and Y-Axis: The horizontal axis (x-axis) represents the independent variable, while the vertical axis (y-axis) represents the dependent variable.
- Plotting Points: Each point on the graph corresponds to a pair of numbers (x, y), where x is the value on the horizontal axis and y is the value on the vertical axis.
- Graph Shapes: The shape of the graph gives you important clues about the relationship between variables. For example, a straight line indicates a linear relationship, while a curve might indicate a more complex one.
Functions and Their Role
Functions describe the relationship between two variables, where each input (x) is associated with exactly one output (y). This concept is fundamental to understanding how one quantity influences another. Functions can be represented as equations, tables, or graphs, and they allow you to predict outcomes based on the inputs you provide.
- Domain and Range: The domain refers to all possible input values, while the range is the set of possible output values. Understanding these can help you determine which values are valid within a given function.
- Linear vs. Nonlinear: Linear functions create straight-line graphs, while nonlinear functions produce curved graphs. Recognizing these differences can help in identifying the type of function you are working with.
- Transformations: Functions can be transformed by shifting, stretching, or reflecting the graph. Understanding these transformations is key to manipulating and analyzing functions effectively.
By gaining a deeper understanding of graphing and functions, you can better interpret and solve mathematical problems. This knowledge allows you to visualize complex relationships and make predictions with greater accuracy.
Strategies for Solving Word Problems
Word problems often present real-world scenarios that require mathematical thinking to solve. They may seem challenging at first, but with the right approach, they become much easier to manage. The key is to break down the problem into smaller, more manageable steps and translate the information into a mathematical framework. By using effective strategies, you can tackle word problems with confidence and accuracy.
Step 1: Understand the Problem
Before jumping into calculations, it’s important to thoroughly understand the situation being described. Read the problem carefully and highlight the key information, such as quantities, relationships, and what you are asked to find. Identifying what is given and what needs to be determined is the first step in translating the problem into a solvable form.
- Identify the Known Values: These are the numbers and facts that are explicitly mentioned in the problem.
- Determine the Unknowns: These are the values you need to find through calculations or reasoning.
- Look for Keywords: Words like “total,” “difference,” “sum,” and “per” can give you clues about which operation (addition, subtraction, multiplication, or division) to use.
Step 2: Create a Plan and Solve
Once you understand the problem, devise a plan to solve it. This could involve setting up equations, drawing diagrams, or using logical reasoning to simplify the problem. If the problem involves multiple steps, break them down and tackle each part systematically.
- Write an Equation: If the problem involves numbers and relationships, express these mathematically by writing an equation.
- Use Units and Labels: Always include units (such as meters, dollars, etc.) to keep track of what you are calculating. This helps avoid confusion and ensures the solution makes sense.
- Double-Check Your Work: Once you arrive at an answer, revisit the problem and check your work to ensure the solution fits the given information.
By following these steps and applying logical reasoning, you can successfully navigate word problems and apply mathematical concepts to real-life situations. Practice and experience will help you develop a methodical approach, making it easier to solve even the most complex problems.
Reviewing Algebraic Properties and Rules

Understanding the fundamental properties and rules of mathematics is essential for solving various types of problems efficiently. These principles help simplify expressions, solve equations, and ensure consistency in calculations. By revisiting these core rules, you can approach more complex challenges with a clearer strategy and greater confidence. Here, we’ll explore some of the key properties that form the foundation of mathematical problem-solving.
Key Properties of Operations
Mathematical operations are governed by specific properties that dictate how numbers and expressions can be manipulated. Mastering these properties ensures that you can simplify and solve equations correctly. Here are the most essential ones:
- Commutative Property: This property states that the order of addition or multiplication does not affect the result. For example, a + b = b + a and a × b = b × a.
- Associative Property: The way numbers are grouped in addition or multiplication does not change the outcome. For example, (a + b) + c = a + (b + c) and (a × b) × c = a × (b × c).
- Distributive Property: This property describes how multiplication distributes over addition or subtraction. For example, a × (b + c) = a × b + a × c.
Applying These Properties in Equations
Once you have a solid understanding of the basic properties, applying them in equations can help you simplify expressions and solve problems more effectively. Here are some strategies to use these properties:
- Simplify Complex Expressions: Use the distributive property to break down expressions into simpler parts.
- Group Terms: Use the associative and commutative properties to rearrange and group terms in ways that make calculations easier.
- Substitute Values: When solving equations, apply these properties to substitute known values and simplify the problem to a solvable form.
By familiarizing yourself with these rules and properties, you can navigate through problems more efficiently and reduce the chances of making errors. Whether you’re solving basic equations or tackling more advanced topics, these foundational properties are critical to mastering mathematics.
How to Stay Confident During the Test
Maintaining composure and confidence during a challenging assessment is crucial to performing well. When faced with difficult questions, it’s easy to feel overwhelmed, but the key to success lies in staying calm and focused. By applying a few mental strategies and preparation techniques, you can boost your confidence and improve your performance, even under pressure. In this section, we will explore methods for staying confident and managing stress effectively during assessments.
Preparing Mentally Before the Assessment
Confidence often starts before you even begin the assessment. Proper mental preparation helps you feel ready to tackle the questions ahead. Here are some useful tips:
- Practice Regularly: Familiarize yourself with the material by practicing frequently. The more you practice, the more confident you will feel about your abilities.
- Visualize Success: Before the assessment begins, take a few moments to visualize yourself solving problems with ease. This mental exercise can help you approach the assessment with a positive mindset.
- Stay Organized: Prepare all your materials in advance, so you don’t waste time during the assessment. Being organized gives you a sense of control and reduces anxiety.
Managing Stress During the Assessment
It’s natural to feel nervous when facing a series of questions, but managing stress is key to staying focused and performing well. Here are a few techniques to calm your nerves:
- Deep Breathing: When you start to feel anxious, take a deep breath. Deep breathing helps slow your heart rate and reduces feelings of stress.
- Focus on the Process: Instead of worrying about the outcome, focus on solving one problem at a time. Breaking the assessment into smaller steps can make it feel more manageable.
- Stay Positive: Remind yourself that you are prepared. Even if you encounter a challenging question, stay positive and keep moving forward.
Confidence is not just about knowing the material–it’s also about trusting yourself and your abilities. By preparing effectively, managing stress, and staying positive throughout the process, you can approach any assessment with the confidence to succeed.
Post-Assessment Review and Improvement Tips
After completing an assessment, the review process plays a critical role in enhancing your skills and understanding. Reflecting on the questions you encountered, identifying areas where you struggled, and recognizing patterns in your mistakes can provide valuable insights for future success. This phase allows you to learn from your experience and develop a more effective approach to tackling similar challenges moving forward.
Evaluating Your Performance
Once the assessment is complete, it’s essential to carefully evaluate your performance. This helps in pinpointing areas where you may need additional practice. Consider the following steps:
- Analyze Mistakes: Review the questions you answered incorrectly. Understand why you made those errors and whether they were due to misinterpretation, lack of knowledge, or simple mistakes.
- Identify Patterns: If you find that you made similar mistakes on multiple questions, focus on that area. It might indicate a gap in your understanding or an aspect of the material that requires more attention.
- Track Time Management: Reflect on how well you managed your time. Did you spend too much time on certain problems? Were there questions you rushed through? Understanding your pacing can help you refine your approach for next time.
Implementing Improvement Strategies
After identifying areas for improvement, it’s time to implement strategies to strengthen your skills. These tips can help you enhance your knowledge and performance:
- Target Weak Areas: Dedicate extra time to practicing the concepts or skills you found challenging. Use additional resources or seek guidance if needed to reinforce your understanding.
- Practice Regularly: Consistent practice is key to mastering any skill. Set aside time each week to work through similar problems and solidify your knowledge.
- Use a Step-by-Step Approach: When practicing, break down problems into smaller steps. This method will help you stay organized and ensure that you fully understand each part of the process.
By reviewing your performance after each assessment and focusing on areas for growth, you can continuously improve and build the confidence needed to tackle future challenges with greater success.