
In this part of the learning material, you will delve into core mathematical principles that are essential for developing strong problem-solving skills. The focus is on understanding the underlying structure of equations and their real-world applications. This knowledge serves as a foundation for tackling more advanced topics in the subject.
Throughout this section, you will explore strategies for efficiently working through different types of problems. Emphasis is placed on simplifying complex steps and identifying patterns that make solving easier. By mastering these concepts, you will gain confidence in applying mathematical techniques to a variety of challenges.
Whether you’re reviewing the material for the first time or reinforcing your existing skills, this guide will provide clear explanations and practical examples. With consistent practice and a methodical approach, you will be well-equipped to succeed and build a solid understanding of the topic at hand.
Algebra Nation Section 5 Answers Overview
This segment of the material focuses on building a deeper understanding of key mathematical concepts. It introduces techniques for solving problems and exploring the relationships between various equations. The main objective is to develop a comprehensive approach to tackling complex mathematical challenges by breaking them down into manageable steps.
In this part, you’ll learn how to apply fundamental principles to diverse problems, recognizing patterns and connections that simplify the process. It’s designed to help you gain clarity and confidence in approaching problems that require both logical reasoning and mathematical manipulation. Mastery of these techniques is crucial for progressing through more advanced topics with ease.
Approach to Problem-Solving
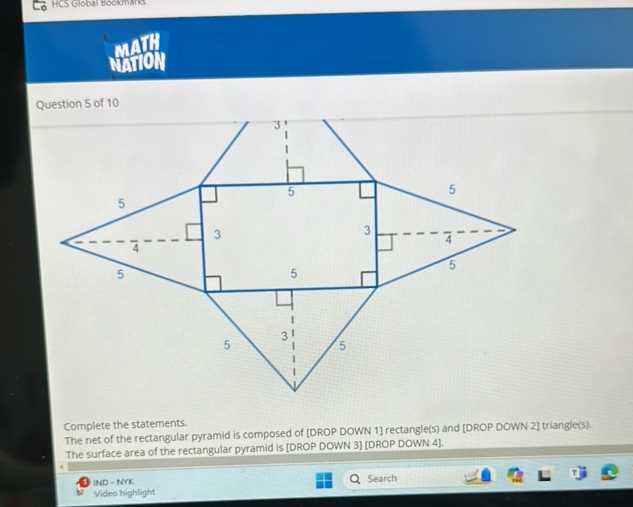
The core of this section is to refine problem-solving strategies. It provides an organized method for addressing each challenge systematically, ensuring no important step is overlooked. Understanding the process is just as important as reaching the solution itself, and this section emphasizes the value of both precision and confidence when working through exercises.
Improving Computational Skills
By practicing the exercises in this section, learners can enhance their computational abilities, ensuring that they are prepared for more complex tasks in the future. Regular engagement with these problems sharpens one’s skills and strengthens the ability to navigate through mathematical tasks effectively.
Key Concepts in Algebra Nation
This part of the course introduces essential mathematical ideas that form the foundation for solving a wide range of problems. The focus is on understanding the structures and relationships that underpin mathematical operations, allowing you to approach each problem with a clear strategy. A strong grasp of these key concepts will improve your ability to tackle even the most challenging tasks.
Understanding variables, equations, and expressions is central to this material. You’ll learn how to manipulate these elements effectively and use them to form logical solutions. The ability to simplify complex problems into smaller, manageable components is one of the primary skills developed in this section, preparing you for more advanced topics down the road.
Step-by-Step Guide to Section 5
This guide provides a detailed approach to mastering the material in this part of the course. It breaks down each problem into smaller, manageable steps, ensuring that learners can follow the process with clarity. By understanding the sequence of operations and logical steps, you will be able to tackle complex challenges with confidence.
Starting with basic concepts, the guide gradually leads you through more intricate calculations, highlighting important techniques along the way. Each step is designed to reinforce your understanding and help you build a strong foundation for solving future problems. By carefully following the instructions and practicing regularly, you’ll be able to master the skills needed to excel.
Understanding Algebraic Expressions Clearly
Grasping the structure of mathematical statements is essential for solving problems efficiently. These expressions represent relationships between numbers, variables, and operations. By learning how to interpret and simplify them, you’ll be able to approach problems with a clearer perspective and find solutions faster.
It’s important to understand how terms and coefficients interact within an expression. The process of combining like terms, applying the correct operations, and recognizing patterns all contribute to simplifying complex problems. Mastering these skills allows you to manipulate mathematical statements more effectively and makes problem-solving much smoother.
Once you are comfortable with the basic elements of an expression, such as constants and variables, you can start exploring more advanced techniques. With continued practice, your ability to handle complex equations will grow, making it easier to tackle a wide variety of mathematical challenges.
Solving Equations in Section 5
In this part of the material, you will focus on the process of finding the values that satisfy a given mathematical relationship. Solving these problems involves applying logical steps and manipulating the given expressions until you isolate the unknown variable. With practice, you will learn how to handle various types of equations efficiently.
Here are some key steps to keep in mind when solving equations:
- Identify the unknown: Begin by recognizing what variable or term you need to solve for.
- Isolate the variable: Use operations like addition, subtraction, multiplication, or division to get the variable on one side of the equation.
- Simplify both sides: Combine like terms and reduce the equation to its simplest form.
- Check your solution: After solving, substitute your value back into the original equation to ensure it holds true.
By following these steps, you’ll develop a systematic approach to solving equations, which is essential for progressing to more complex topics. With consistent practice, the process will become more intuitive, allowing you to tackle increasingly difficult problems with confidence.
Common Mistakes in Algebra Problems
When working through mathematical challenges, it’s easy to make small errors that can lead to incorrect results. Recognizing and understanding these common mistakes is essential for improving problem-solving skills. By identifying these pitfalls, you can avoid them and develop a more accurate approach to solving problems.
Some of the most frequent mistakes include:
- Misapplying the order of operations: Failing to follow the correct sequence of operations (PEMDAS) can lead to incorrect answers. Always prioritize parentheses, exponents, multiplication, and division before addition and subtraction.
- Combining unlike terms: One of the most common errors is trying to add or subtract terms that are not similar. Be sure to combine only like terms with the same variable or constant.
- Forgetting to distribute: When dealing with expressions that require distribution, it’s easy to overlook distributing a factor across terms inside parentheses, leading to incorrect simplifications.
- Sign errors: Incorrectly handling negative signs during addition, subtraction, or multiplication can result in significant mistakes. Always double-check signs when performing operations.
By being mindful of these common errors and practicing regularly, you can refine your problem-solving process and become more confident in your ability to handle various mathematical tasks accurately.
Tips for Success in Algebra Nation
Achieving success in mathematical studies requires more than just completing exercises. It’s about developing a systematic approach to learning, understanding core concepts, and practicing consistently. By following a few key strategies, you can improve your skills and boost your confidence as you tackle challenging problems.
Effective Study Habits
To excel in this subject, it’s important to cultivate habits that support long-term understanding:
- Practice regularly: Consistent practice is essential for reinforcing concepts and improving problem-solving speed. The more you practice, the more confident you’ll become.
- Break down problems: Don’t try to solve problems all at once. Break them into smaller, manageable steps. This will help you stay focused and avoid feeling overwhelmed.
- Review past material: Don’t just move on to new topics without revisiting previous ones. A strong foundation is critical for understanding more advanced concepts.
Seeking Help and Resources
It’s also important to utilize available resources and ask for help when needed:
- Ask questions: If you’re stuck, don’t hesitate to seek clarification from a teacher, tutor, or classmate. Understanding the ‘why’ behind each step is just as important as finding the correct solution.
- Use additional resources: Supplement your studies with online tutorials, practice problems, and forums where you can discuss challenging topics with peers.
- Stay organized: Keep track of assignments, deadlines, and areas where you need improvement. Being organized will help you manage your time and avoid last-minute stress.
By following these tips and staying committed to the learning process, you’ll be well on your way to mastering the material and achieving success in your mathematical studies.
How to Approach Word Problems

Word problems often seem more challenging than straightforward equations, as they require not only mathematical skills but also the ability to translate a real-world scenario into a solvable equation. However, with the right approach, these problems can become easier to handle. The key is to break down the problem into manageable parts and systematically translate each piece of information into mathematical terms.
Here’s a simple strategy to follow when approaching word problems:
| Step | Description |
|---|---|
| 1. Read the problem carefully | Make sure to read the problem thoroughly and understand what is being asked. Highlight important numbers and key terms. |
| 2. Identify the unknown | Determine which variable or quantity you need to solve for and define it clearly. |
| 3. Translate the words into an equation | Convert the information into a mathematical expression or equation, using the known values and operations. |
| 4. Solve the equation | Use appropriate methods to solve the equation or simplify the expression to find the unknown. |
| 5. Verify the solution | Once you’ve found a solution, substitute it back into the original problem to ensure it makes sense. |
By following these steps, you’ll improve your ability to solve word problems effectively. Practice with different scenarios will help you recognize patterns and develop strategies to handle more complex problems with confidence.
Using Algebraic Formulas Efficiently
Mastering mathematical formulas is essential for solving complex problems with ease. Formulas provide a structured way to calculate specific values and relationships, allowing you to apply consistent methods to a variety of challenges. However, knowing how to use these formulas effectively is just as important as memorizing them.
Steps to Apply Formulas Correctly
To use mathematical formulas effectively, follow these steps:
- Understand the formula: Before applying a formula, make sure you fully understand each variable and what it represents. This will prevent confusion and mistakes.
- Substitute values carefully: Always double-check the values you are plugging into the formula. Ensure they correspond correctly to the variables in the equation.
- Simplify step by step: Break down the formula and simplify each part before solving. This helps prevent errors in calculation and ensures a more accurate result.
Tips for Efficiency
To save time and improve accuracy when using formulas, consider these additional tips:
- Familiarize yourself with common formulas: Practice frequently-used formulas so they become second nature. This reduces the time spent looking them up during problem-solving.
- Use units correctly: Always ensure that the units of measurement are consistent across all terms in the formula, and convert them if necessary.
- Check your work: After applying a formula, recheck your steps to ensure you’ve followed the correct process and avoided mistakes.
By following these strategies, you will be able to apply mathematical formulas more efficiently, leading to faster and more accurate results in your problem-solving tasks.
Helpful Strategies for Section 5
To effectively solve problems, it’s essential to have a clear approach. Breaking down complex tasks into manageable steps allows for better focus and minimizes the chances of error. By applying specific strategies, you can streamline your process and tackle each challenge with confidence. These strategies not only help in understanding the problem but also lead to faster, more accurate solutions.
Effective Techniques to Implement
Below are some practical strategies to enhance your problem-solving skills:
| Technique | Explanation |
|---|---|
| Analyze the Problem Thoroughly | Before starting, take time to fully understand the problem. Identify all given information and what is being asked. |
| Break It Down Into Steps | Divide the problem into smaller, easier-to-manage components. Tackle each part individually to simplify the overall task. |
| Use Logical Progression | Approach each part of the problem logically. Apply known principles and build on them step-by-step to reach the solution. |
| Double-Check Your Work | After solving the problem, review each step to verify the accuracy of your calculations and reasoning. |
Additional Tips for Success
To further boost your efficiency, try incorporating these additional strategies:
- Organize Your Notes: Keep your work neat and structured to avoid confusion. Organized notes help you track progress and spot errors more easily.
- Identify Patterns: Look for patterns in the problem that can guide your approach and reveal shortcuts for faster solutions.
- Stay Calm and Focused: Avoid rushing through problems. Take your time to think critically and stay focused on each step of the process.
By incorporating these strategies into your approach, you’ll be able to solve problems more efficiently and with greater accuracy, ultimately improving your overall performance.
Practice Problems and Solutions
Working through practice problems is one of the most effective ways to reinforce concepts and develop a deeper understanding of mathematical techniques. By regularly solving a variety of problems, you can sharpen your skills, identify common mistakes, and build confidence in your problem-solving abilities. This section presents a collection of practice problems, along with detailed solutions, to help guide you through key concepts and improve your proficiency.
Example Problems
Below are a few example problems for you to practice. Follow the step-by-step process to solve them, and compare your solutions with the provided answers.
- Problem 1: Solve for x: 5x + 3 = 18
- Problem 2: Simplify the expression: 3(2x – 4) + 7x
- Problem 3: Solve the equation: 4x – 5 = 3x + 7
- Problem 4: Factor the quadratic expression: x² – 5x + 6
Solutions and Step-by-Step Guide
Here are the solutions to the problems listed above. Review each step to ensure you understand how to reach the correct answer.
- Solution to Problem 1: To solve 5x + 3 = 18, first subtract 3 from both sides: 5x = 15. Then, divide both sides by 5 to get x = 3.
- Solution to Problem 2: Simplify 3(2x – 4) + 7x by first distributing the 3: 6x – 12 + 7x. Combine like terms to get 13x – 12.
- Solution to Problem 3: Solve 4x – 5 = 3x + 7 by subtracting 3x from both sides: x – 5 = 7. Add 5 to both sides to get x = 12.
- Solution to Problem 4: Factor x² – 5x + 6 by finding two numbers that multiply to 6 and add up to -5. The factors are -2 and -3, so the factored form is (x – 2)(x – 3).
By practicing these problems and following the solutions, you’ll improve your ability to solve similar challenges in the future. Regular practice is key to mastering any mathematical topic.
Breaking Down Complex Algebraic Steps
Solving advanced mathematical problems often involves multiple steps, each requiring careful attention and logical reasoning. When faced with intricate calculations or lengthy equations, breaking the process into smaller, manageable parts can make the task easier to understand and solve. This approach helps eliminate confusion and ensures accuracy throughout each stage of the solution.
One effective method is to isolate different components of the problem and tackle them individually before combining the results. By recognizing patterns and understanding the relationships between variables, the complexity of the problem can be greatly reduced. With each step, it is crucial to stay organized and methodical, applying fundamental principles to work through the solution efficiently.
For example, when dealing with equations that involve fractions, exponents, or multiple variables, it’s helpful to simplify each part before attempting to solve for the unknowns. This ensures that no step is overlooked, and that each part of the problem is handled with precision. By gradually building from one step to the next, you can approach even the most complex problems with confidence.
Important Mathematical Rules to Remember
When working with mathematical expressions and equations, it’s essential to keep in mind certain foundational rules that guide the problem-solving process. These rules form the bedrock of logical reasoning in mathematics, ensuring that each step is valid and that solutions are accurate. Mastering these principles helps streamline the solving process and provides clarity when facing complex problems.
Order of Operations
The order in which mathematical operations are performed is crucial. The commonly remembered acronym PEMDAS stands for Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). This rule ensures that operations are executed in the correct sequence, preventing errors in calculations.
Distributive Property
The distributive property is another key principle, which states that multiplying a number by a sum is the same as multiplying each addend individually and then adding the products. For example, a(b + c) = ab + ac. This rule simplifies expressions and helps in solving equations efficiently by breaking down complex terms.
By mastering these fundamental rules, you ensure that you approach each problem logically and consistently, improving both accuracy and efficiency in solving mathematical challenges.
How to Check Your Work

Verifying the accuracy of your calculations is an essential part of solving any mathematical problem. By reviewing each step of the process, you can identify and correct potential errors, ensuring that your final solution is both accurate and reliable. A systematic approach to checking your work can prevent simple mistakes from affecting your results.
Review Each Step Thoroughly
Start by carefully reviewing each individual step of your solution. Make sure that all operations were performed correctly and that you adhered to the appropriate rules. Pay particular attention to common mistakes, such as sign errors or misapplied formulas. Rewriting your steps can help highlight any overlooked mistakes.
Substitute Back into the Original Equation
Another effective method for checking your work is to substitute your final solution back into the original equation. This process helps confirm that the values you found satisfy all conditions of the problem. If both sides of the equation are equal after substitution, then your solution is likely correct. If not, review your steps to identify where the error may have occurred.
By following these steps, you can ensure the correctness of your work and boost your confidence in your solution. Taking the time to check each part of the process is key to achieving accurate and reliable results.
Mastering Section 5 with Confidence
Achieving mastery in complex mathematical concepts requires a blend of consistent practice, clear understanding, and effective strategies. Developing confidence in solving challenging problems is key to mastering any topic. With the right approach, you can strengthen your skills, overcome difficulties, and tackle each task with certainty.
Building a Strong Foundation
The first step towards success is ensuring a solid understanding of the core principles involved. Without this foundation, more advanced concepts can become overwhelming. Focus on reinforcing the basics, as they provide the necessary groundwork for solving more complicated problems later.
Effective Strategies for Problem-Solving
Adopting efficient problem-solving techniques can significantly enhance your ability to solve problems quickly and accurately. Break down problems into smaller, manageable steps and approach them systematically. Staying organized and reviewing your work will help you catch potential errors before they become obstacles.
| Strategy | Benefit |
|---|---|
| Practice Regularly | Reinforces understanding and builds confidence |
| Focus on Mistakes | Identifying errors enhances learning and problem-solving skills |
| Break Problems into Steps | Makes complex tasks more manageable and reduces overwhelm |
By combining a solid grasp of the fundamentals with strategic practice and problem-solving methods, you will gain the confidence needed to approach even the most challenging problems with ease. Keep practicing, stay focused, and success will follow.
Resources for Further Study
To deepen your understanding and enhance your problem-solving skills, it’s essential to have access to a variety of learning materials and resources. Whether you’re looking to review foundational concepts or explore more advanced topics, the right tools can help you achieve your goals. These resources range from online tutorials to interactive exercises, all designed to support your learning journey.
Online Learning Platforms
There are many digital platforms that offer comprehensive lessons, interactive quizzes, and expert explanations to help you grasp complex concepts. These platforms often provide step-by-step guidance and allow you to practice at your own pace.
- Khan Academy – Offers free courses and exercises on a variety of mathematical topics with instructional videos.
- Coursera – Provides online courses from top universities, often with a focus on problem-solving techniques.
- edX – Features courses from leading institutions that can help you build a strong foundation in mathematical reasoning.
Books and Printed Guides
While online resources are highly valuable, printed materials can also serve as an excellent supplement to your learning. Books and workbooks provide a structured approach to understanding key concepts and practicing problem-solving techniques.
- “The Art of Problem Solving” by Richard Rusczyk – A comprehensive series that breaks down complex problems and strategies.
- “How to Solve It” by George Pólya – Focuses on the methods and logic behind solving mathematical problems.
- Workbooks – Available for targeted practice on specific topics, helping you master the skills needed for success.
By utilizing these diverse resources, you can expand your knowledge, reinforce your skills, and approach more advanced topics with confidence. Combining different types of learning materials will help ensure a well-rounded mastery of mathematical concepts and techniques.
Benefits of Practice
Engaging in consistent practice is a key factor in mastering any subject. By focusing on repeated exercises, learners can reinforce concepts, identify areas of weakness, and improve their problem-solving speed and accuracy. Structured practice offers multiple advantages for anyone looking to sharpen their skills and deepen their understanding of mathematical principles.
Key Advantages of Regular Practice
- Improved Retention: The more you practice, the more likely you are to retain critical information and formulas, making it easier to recall during assessments or real-world applications.
- Enhanced Problem-Solving Speed: Regular practice helps build familiarity with common problem types, allowing for quicker identification of solutions and more efficient problem-solving.
- Increased Confidence: Repeated exposure to challenging problems builds confidence. As you become more comfortable with concepts, tackling more complex issues becomes less intimidating.
- Better Understanding of Core Concepts: Practice helps connect abstract ideas to tangible outcomes, allowing for a deeper understanding of the material.
- Immediate Feedback: Many practice platforms offer instant feedback, which helps learners recognize mistakes, correct them, and prevent misunderstandings from developing further.
How Practice Accelerates Learning
- Identifying Patterns: Through regular exercises, learners begin to recognize patterns in problems and solutions, making it easier to solve similar tasks in the future.
- Building Fluency: Like learning a new language, frequent practice leads to fluency in solving various types of problems, which is crucial for success in more advanced topics.
- Strengthening Critical Thinking: Consistent practice encourages students to approach problems from multiple angles, improving logical thinking and reasoning abilities.
Ultimately, consistent practice not only reinforces the content learned but also fosters a positive attitude toward learning. By committing to regular exercises and focusing on areas that need improvement, you can make steady progress and achieve greater success in mastering the material.
Final Tips for Success
To truly excel in mastering mathematical concepts, it’s important to incorporate effective strategies into your study routine. Success comes from not only understanding the material but also applying it with confidence. By following a few key tips, you can enhance your learning experience, stay motivated, and improve your performance in assessments.
Effective Study Habits
- Stay Organized: Keeping track of assignments, notes, and deadlines will help you stay on top of your learning. Use a planner or digital tools to organize your study schedule.
- Break Down Complex Problems: Large problems can be overwhelming. Divide them into smaller, manageable parts and solve each step methodically.
- Practice Consistently: Make practice a daily habit. Repetition builds familiarity, reinforcing key concepts and improving problem-solving skills.
- Review Mistakes: Take time to review your errors and understand why the correct answer works. This helps avoid repeating mistakes and deepens understanding.
Staying Motivated
- Set Clear Goals: Set realistic short-term and long-term goals for each topic. Having a clear target will keep you focused and motivated.
- Seek Help When Needed: If you’re struggling with a particular concept, don’t hesitate to ask for help from a teacher, peer, or online resources. Understanding early will prevent confusion later.
- Stay Positive: Approach challenges with a positive mindset. Believe in your ability to succeed, and keep a growth-oriented attitude.
By integrating these tips into your study plan, you can approach your work with clarity and confidence, ensuring continuous improvement and success in mastering the material.