Algebra Nation Test Yourself Section 1 Answers

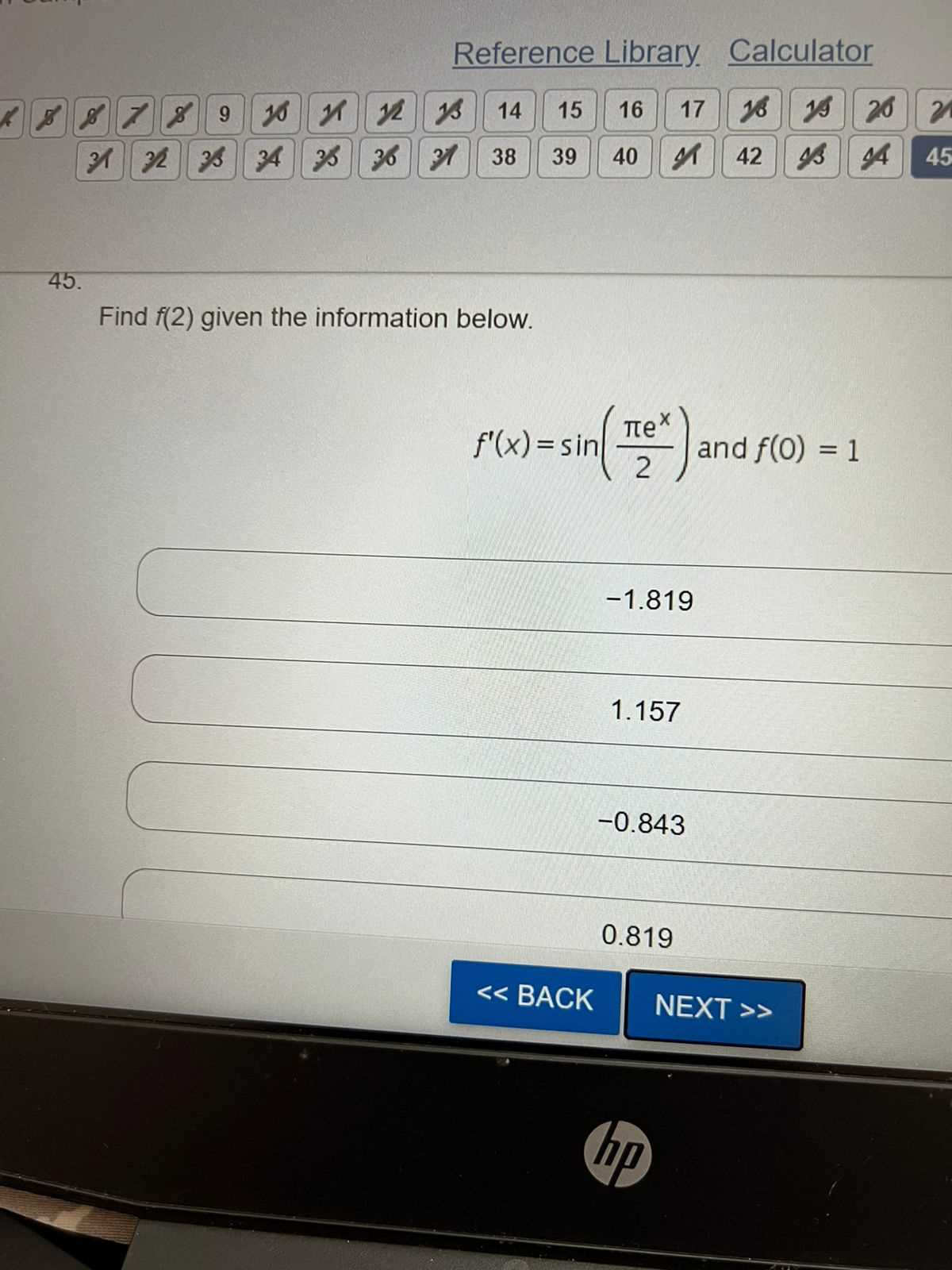
In this segment, students can explore a variety of practice questions designed to strengthen foundational knowledge and problem-solving skills. The exercises challenge learners to apply critical thinking and refine their approach to different mathematical concepts.

Building confidence through step-by-step solutions helps users understand common approaches and strategies, ensuring a deeper grasp of the material. By reviewing each response, individuals can learn from their mistakes and improve their performance in future challenges.

The key to mastering any subject lies in consistent practice and understanding where improvements can be made. Engaging with this material will allow learners to gain a more thorough understanding, which will be valuable in more advanced topics.

Algebra Nation Test Yourself Answers Overview

This segment provides a comprehensive look at the available practice questions and solutions designed to enhance your mathematical skills. It offers a structured way for learners to evaluate their understanding of key concepts, guiding them through the process of mastering essential topics.

Each question has been carefully crafted to test various aspects of mathematical reasoning and to support progress at an individual pace. By engaging with the material, students can strengthen their problem-solving abilities and gain more confidence in their skills.

To help users better grasp the content, a detailed breakdown of the responses is provided. This allows for a thorough analysis of each solution and offers insight into common pitfalls to avoid.

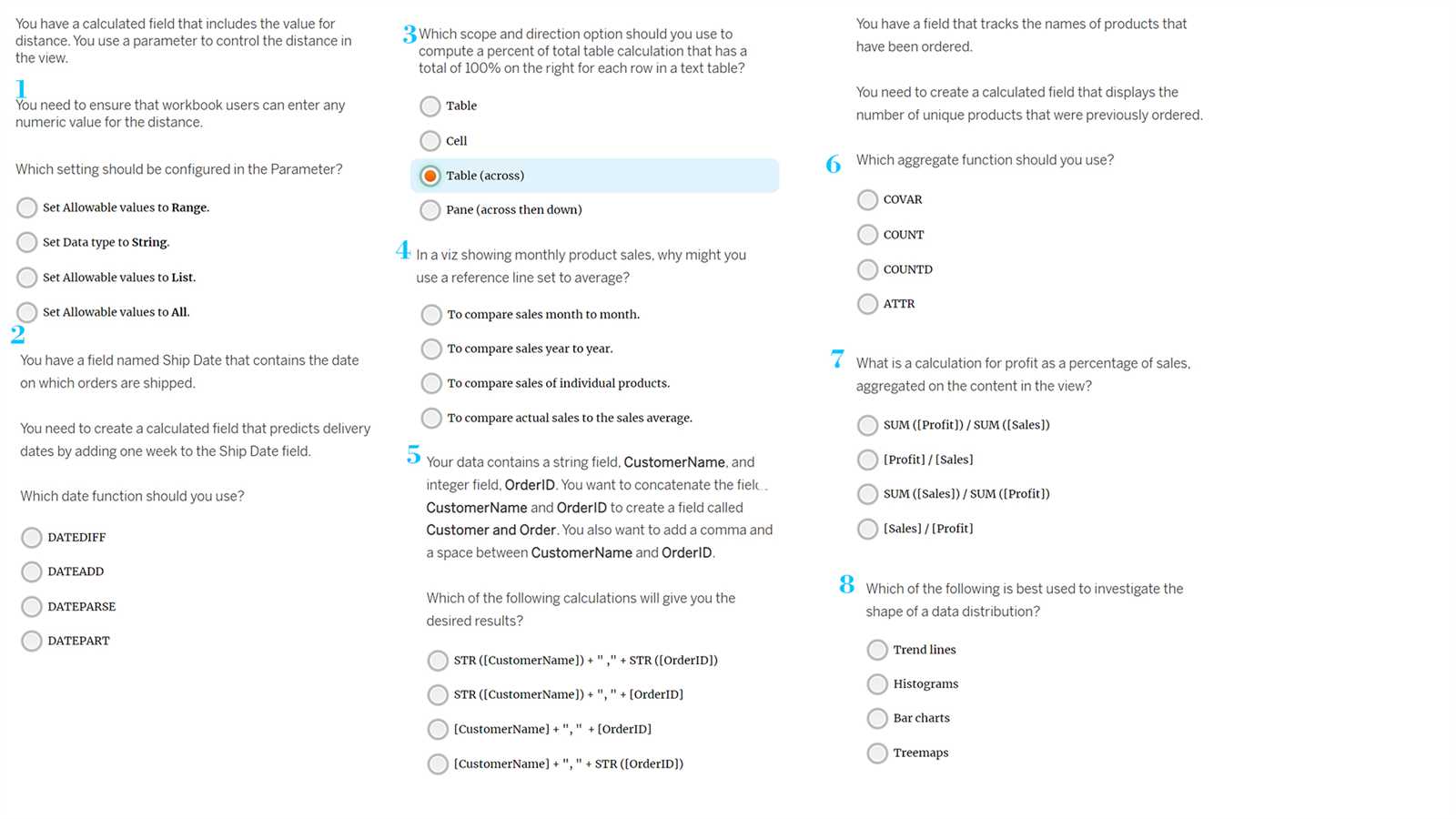
Topic	Concepts Tested	Key Focus Areas
Basic Operations	Arithmetic, Fractions, Decimals	Understanding basic calculations and operations
Equations	Linear Equations, Solving for Variables	Finding solutions and manipulating expressions
Graphing	Plotting Points, Interpreting Graphs	Visualizing equations and relationships
Word Problems	Application of Mathematical Concepts	Translating problems into mathematical language

How to Access Section 1 Answers

To view the solutions for the initial set of practice problems, begin by logging into the platform and navigating to the appropriate section of the learning module. Once there, you will find a dedicated area where the correct responses and step-by-step explanations are provided.

Accessing the solutions is straightforward, and users can follow the prompts on the page to either review individual answers or download a full set of solutions for a deeper analysis. This resource is designed to help you understand the methodology behind each problem and refine your approach to similar challenges.

Ensure that you carefully review the provided solutions to fully comprehend the reasoning behind each step. This will enable you to improve your problem-solving techniques and avoid common errors in future exercises.

Understanding Algebra Nation Practice Tests

This practice resource is designed to help learners solidify their understanding of key mathematical concepts by offering a series of exercises that simulate real-world problem-solving scenarios. The challenges are structured to test various skills, from basic calculations to more complex problem-solving techniques, enabling individuals to track their progress over time.

Each exercise is crafted to address specific areas of learning, ensuring that users can focus on strengthening their weaknesses while reinforcing their strengths. As you engage with these activities, you will gain a deeper insight into the problem-solving process and the logical steps required to arrive at accurate solutions.

The goal of these practice activities is to promote a more comprehensive understanding of the material. By reviewing the problems and solutions, students can enhance their analytical thinking, making it easier to approach similar challenges in future learning contexts.

Step-by-Step Guide to Answering Questions

To effectively tackle each problem, it’s essential to follow a clear and organized approach. Breaking down complex questions into smaller, manageable steps ensures that you can address each part of the problem methodically and with confidence. This structured approach helps prevent errors and provides a clearer path toward finding the correct solution.

1. Read the Problem Carefully

Before diving into calculations, take time to thoroughly understand the problem. Identify the key information, variables, and what the question is specifically asking. This initial step helps you focus on what is essential and prevents confusion later on.

2. Plan Your Approach

After understanding the question, plan how you will solve it. Determine which mathematical operations or strategies are needed and in what order. A well-thought-out plan can make the process more efficient and reduce the likelihood of mistakes.

Focus on each step rather than rushing to the final answer. Be methodical, and use logical reasoning to ensure each part of the solution is accurate. This process will not only help you find the correct answers but also strengthen your problem-solving skills for future challenges.

Importance of Section 1 in Mastery

The first part of any practice module is crucial for building a strong foundation in mathematical reasoning. It focuses on introducing basic concepts and ensuring that learners have the necessary skills to tackle more advanced material. A solid grasp of these initial concepts is essential for success in more complex problems later on.

Key Benefits of Starting with Section 1

Foundational Knowledge: This section helps to establish core skills that are required for solving increasingly challenging problems.
Confidence Boost: Mastering the early stages provides learners with the confidence to approach more difficult topics with ease.
Critical Thinking Development: The problems encourage logical thinking and problem-solving abilities, which are vital for success in future learning.

Skills Developed in the First Part

Understanding key mathematical operations
Strengthening problem-solving strategies
Building the ability to break down complex problems into manageable steps

Mastering this section is an important milestone in any learning journey, laying the groundwork for tackling more intricate concepts in later modules. By thoroughly engaging with the material, learners can ensure a stronger understanding and smoother progression through the entire curriculum.

Common Mistakes in Test Yourself Section 1

Even experienced learners can make common errors when approaching practice exercises. These mistakes often arise from misinterpreting the problem, rushing through calculations, or overlooking small details. Identifying and correcting these errors is crucial for improving accuracy and overall problem-solving skills.

Typical Errors to Watch For

Misreading the Problem: Failing to fully comprehend what the question is asking can lead to incorrect approaches and answers. Always take time to understand the requirements before starting calculations.
Skipping Steps: Rushing through the process without following each logical step can result in missing key elements of the solution. It’s important to work through problems systematically.
Calculation Mistakes: Simple arithmetic errors can easily occur, especially under time pressure. Double-checking your work can help prevent these avoidable mistakes.
Ignoring Units: In some problems, ignoring units or dimensions can lead to confusion or inaccurate results. Always ensure units are properly accounted for when solving problems.

How to Avoid These Mistakes

Read the Problem Carefully: Ensure you fully understand the context and what is being asked before proceeding.
Follow a Step-by-Step Process: Never skip steps and always check each stage of your work for consistency and accuracy.
Review Your Calculations: Make it a habit to double-check all arithmetic and operations before finalizing your answer.
Keep Track of Units: Ensure that you account for units, whether they are numbers, variables, or measurements, throughout the problem-solving process.

By recognizing these common pitfalls and adjusting your approach, you can significantly improve your performance and understanding, ensuring stronger problem-solving skills in the long run.

Tips for Improving Algebra Skills

Strengthening your mathematical abilities requires consistent practice and a strategic approach to learning. By refining key concepts and mastering problem-solving techniques, you can enhance your overall performance. Here are some effective strategies to help you improve your skills and gain more confidence in tackling complex problems.

Key Strategies for Improvement

Practice Regularly: Regular practice helps reinforce concepts and solidify understanding. The more problems you solve, the more familiar you become with different methods and techniques.
Break Down Complex Problems: Instead of rushing through difficult problems, break them into smaller, more manageable steps. This makes the problem less intimidating and helps you focus on solving each part individually.
Review Mistakes: After completing an exercise, carefully review any mistakes you made. Understanding where you went wrong allows you to avoid similar errors in the future.
Use Visual Aids: Diagrams, charts, and graphs can often help make abstract concepts more tangible and easier to understand. Visualizing problems can provide a clearer path to the solution.

Additional Techniques for Mastery

Work with Peers: Discussing problems and solutions with others can expose you to different perspectives and enhance your problem-solving skills.
Seek Feedback: Don’t hesitate to ask for help or feedback from a tutor or instructor. Constructive feedback is essential for growth and improvement.
Stay Patient: Building skills takes time, so remain patient and persistent. Progress might be gradual, but consistent effort leads to mastery.

By integrating these strategies into your study routine, you can develop a deeper understanding and become more proficient in mathematical problem solving.

Key Concepts Covered in Section 1

This portion of the material introduces foundational principles that are essential for progressing in the subject. The concepts explored here lay the groundwork for tackling more advanced topics, providing a deeper understanding of the core skills required. By mastering these ideas, students can strengthen their problem-solving techniques and approach more complex challenges with confidence.

Fundamental Ideas Explored

Basic Operations: Understanding the fundamental operations such as addition, subtraction, multiplication, and division forms the basis for solving problems efficiently.
Equations and Variables: The concept of variables and how they interact within equations is explored, helping students to model real-world scenarios and solve for unknowns.
Patterns and Relationships: Recognizing and working with mathematical patterns helps in identifying solutions and drawing connections between different mathematical elements.
Order of Operations: Learning the correct sequence for performing operations ensures accurate results when solving problems involving multiple steps.

Advanced Concepts for Progression

Understanding how to manipulate expressions and simplify them provides a solid foundation for solving more complex problems in future topics.
Mastering the relationships between different mathematical elements allows for a more comprehensive understanding and application of key ideas.
Applying concepts to real-world situations ensures that students can relate abstract ideas to practical scenarios, improving their overall problem-solving abilities.

By gaining a clear understanding of these essential concepts, learners can build a strong mathematical foundation that prepares them for more advanced topics and problem-solving techniques in the subject.

Strategies for Solving Problems

Effectively solving mathematical problems requires a combination of logical thinking, organization, and a solid understanding of fundamental principles. Having a structured approach can make even the most complex problems more manageable. By applying various strategies, students can navigate through calculations and equations with greater ease and accuracy.

Essential Techniques for Success

Understand the Problem: Carefully read through the problem to identify key information, such as the variables, operations, and what is being asked. Clarifying these points at the start will help guide your solution process.
Break It Down: If the problem seems complex, break it into smaller, more manageable parts. Solve each step individually, ensuring that you tackle each concept methodically before moving on to the next.
Use Visual Tools: Diagrams, charts, or even simple sketches can often help visualize the relationships between variables, making it easier to identify patterns and relationships.
Check Your Work: After completing a problem, go over your steps to ensure that you haven’t missed any crucial details or made simple calculation errors. Verifying your results helps prevent minor mistakes from becoming bigger issues.

Advanced Approaches for Complex Problems

Substitution: For equations with multiple variables, substitution allows you to replace one variable with an equivalent expression, simplifying the problem.
Elimination: When dealing with systems of equations, elimination is an effective method for removing one variable at a time, making it easier to solve for the others.
Trial and Error: For more challenging problems, trying different values or approaches can sometimes reveal the correct solution, especially when patterns or relationships are hard to identify immediately.

By practicing these strategies, learners can develop a systematic and effective approach to solving mathematical challenges, building both their confidence and skill in the process.

How Section 1 Prepares You for Mathematics

The first part of the learning material is designed to build a solid foundation in mathematical reasoning and essential problem-solving techniques. It introduces core concepts that are crucial for tackling more advanced mathematical challenges. By focusing on these fundamental skills, this section prepares learners to approach complex equations and scenarios with confidence and clarity.

Building Core Mathematical Skills

Understanding Variables and Expressions: This section introduces the idea of variables and expressions, helping students grasp how unknown quantities are represented and manipulated in mathematical situations.
Developing Operational Fluency: Mastering basic operations such as addition, subtraction, multiplication, and division is essential. These operations are the building blocks for solving more intricate problems and understanding their underlying principles.
Recognizing Patterns: Learning how to identify mathematical patterns plays a key role in solving problems efficiently. This skill helps in recognizing trends and forming strategies to find solutions more quickly.
Enhancing Problem-Solving Strategies: The section emphasizes breaking down problems into manageable steps, helping learners approach challenges methodically and reducing the risk of errors.

Preparing for More Advanced Topics

Laying the Groundwork for Equations: By understanding basic mathematical relationships and expressions, learners are well-prepared to solve more complex equations and formulas in future lessons.
Strengthening Logical Thinking: The section fosters logical reasoning, which is essential for analyzing and solving problems across a variety of mathematical topics, including higher-level concepts.

By mastering the ideas presented in this section, learners establish a strong mathematical foundation that serves as a stepping stone to mastering more advanced topics in the subject.

Using Solutions to Enhance Your Learning

Examining the solutions to problems is a crucial part of deepening understanding and reinforcing knowledge. By reflecting on the process behind each answer, learners can identify the strategies and methods that lead to correct results. This approach not only helps in reinforcing concepts but also aids in avoiding common mistakes, building a stronger grasp of the material.

When you study solutions, focus on the reasoning and steps that were taken to arrive at the conclusion. Break down each step to see how different operations and rules are applied. This enables you to understand the logic behind each calculation and how to apply the same reasoning to other problems.

Moreover, revisiting mistakes in the solutions is just as important. Identifying where you went wrong helps you understand the nuances of the concepts, preventing similar errors in the future. This reflection promotes growth, helping to solidify the material for long-term retention.

Ultimately, using solutions as a learning tool is about more than just knowing the correct answer–it’s about understanding the path to it, refining your approach, and becoming more confident in your problem-solving skills.

Reviewing Solutions for Better Understanding

Carefully reviewing the steps and reasoning behind each solution is an essential part of mastering any subject. By taking the time to understand how a result was achieved, learners can strengthen their knowledge and ensure that they have fully grasped the concepts involved. This process allows for a deeper comprehension and ensures that learning is both thorough and effective.

Identifying Key Concepts in Solutions

When reviewing solutions, focus on the core principles and techniques used to solve the problem. Understanding why certain methods were chosen and how they apply to different scenarios helps to reinforce the material and make it easier to recall in the future. Breaking down each step allows learners to internalize important rules and apply them with confidence.

Learning from Mistakes

In addition to understanding the correct approach, reviewing mistakes is equally valuable. By examining where things went wrong, learners can identify misunderstandings or gaps in their knowledge. Correcting these errors ensures progress and helps prevent the same mistakes from occurring again, ultimately improving overall problem-solving abilities.

By thoroughly reviewing solutions, learners not only gain a clearer understanding of the material but also develop stronger critical thinking and problem-solving skills that will serve them well in more advanced challenges.

Benefits of Practice Questions

Engaging with practice problems offers significant advantages for learners seeking to improve their skills. By repeatedly working through different types of questions, students can enhance their understanding of concepts and become more adept at applying them in various situations. Regular practice fosters confidence and reduces anxiety when facing real assessments, making it a crucial element of the learning process.

Building Problem-Solving Skills

Consistent practice challenges the mind and helps students develop effective problem-solving strategies. Each question presents a unique set of conditions that require thoughtful analysis, encouraging learners to think critically and explore various approaches. Over time, this process strengthens mental flexibility and prepares students to tackle more complex problems with ease.

Tracking Progress and Identifying Weak Areas

Working through practice problems allows learners to track their progress and identify areas where they may need additional focus. By reviewing solutions, students can pinpoint specific concepts or techniques that require further attention. This targeted approach ensures that learning is efficient and helps prevent misunderstandings from persisting.

Incorporating practice questions into study routines provides a structured way to reinforce knowledge, build confidence, and refine problem-solving abilities. It serves as an indispensable tool for long-term academic success.

How Practice Enhances Problem-Solving

Engaging in focused exercises is a powerful way to sharpen problem-solving abilities. By practicing regularly, learners develop a deeper understanding of how to approach different challenges and refine their ability to think critically. The repetition of diverse scenarios helps strengthen cognitive pathways, making it easier to solve problems efficiently and accurately.

Developing Strategic Thinking

Practice allows students to experiment with various strategies and techniques, ultimately identifying the most effective approaches. By solving a range of problems, learners gain experience in breaking down complex tasks into simpler steps, building a structured plan for solving similar challenges in the future. This strategic thinking is a key skill that enhances problem-solving capabilities over time.

Building Confidence Through Repetition

Repetitive practice helps reinforce concepts and increase confidence in tackling problems independently. As learners become more familiar with the types of challenges they might face, their ability to solve them without hesitation improves. This confidence-building aspect reduces anxiety and empowers students to approach future tasks with a positive mindset.

By regularly practicing problem-solving exercises, learners can fine-tune their skills, develop effective strategies, and build the confidence necessary for academic success and real-world applications.

Tracking Progress with Practice Tools

Monitoring progress over time is essential for identifying strengths and areas that need improvement. With the help of targeted learning tools, learners can track their development, see where they excel, and focus on the skills that require further attention. By evaluating performance after each exercise, students can gain a clear picture of their growth and adjust their study methods accordingly.

Visualizing Your Growth

One of the most effective ways to track progress is through visual aids, such as charts or graphs. These tools provide a simple way to see improvements over time, making it easier to stay motivated and focused on goals. By reviewing patterns in performance, learners can better understand their learning trajectory and ensure that they are progressing steadily toward mastery.

Using Feedback to Improve

Detailed feedback is a powerful tool for refining problem-solving strategies. By reviewing the feedback after each practice, students can identify specific mistakes, understand why they occurred, and apply corrections in future exercises. This iterative process of learning from errors helps reinforce the correct methods and fosters continuous improvement.

Time Period	Score	Areas for Improvement
Week 1	75%	Understanding key concepts
Week 2	85%	Accuracy in solving equations
Week 3	90%	Faster problem-solving

By consistently tracking progress, learners can gain insights into their strengths and pinpoint areas for growth. This data-driven approach helps maximize learning outcomes and ensures that each practice session contributes to long-term success.

Maximizing Results with Practice Solutions

Achieving optimal learning outcomes requires not just practice, but also strategic reflection on solutions to problems. By carefully reviewing your approach and the steps involved in each exercise, you can identify what worked well and where improvements are needed. This method of analysis enables more efficient learning and better retention of key concepts, ensuring that each practice session is productive.

Steps for Effective Review

To maximize the benefits of each exercise, follow these steps during your review process:

Identify Mistakes: Look for patterns in your errors, whether they are due to miscalculations, misunderstood concepts, or overlooked details.
Understand the Process: Go over the solution steps carefully to ensure you fully understand the correct approach. This deepens your understanding of the methodology.
Apply New Strategies: Once you recognize areas for improvement, try applying new problem-solving techniques to avoid repeating the same mistakes.
Focus on Weak Areas: After identifying your weaknesses, dedicate extra time to practicing those specific areas to build confidence and skill.

Using Results for Continuous Improvement

Tracking progress after each round of practice is crucial for refining your skills. With a clear understanding of where improvements are needed, you can set specific goals and adjust your study methods to address them. Regularly revisiting challenging areas ensures that learning remains dynamic and leads to consistent advancement.

Set measurable goals: Use performance data to set concrete targets for future practice sessions.
Stay consistent: Regular practice with a focus on weak areas is key to making lasting improvements.
Reassess periodically: Revisit solutions over time to confirm that new strategies are being implemented correctly and consistently.

By applying these methods, you can maximize the benefits of each practice session, ensuring continuous progress and mastery over time.