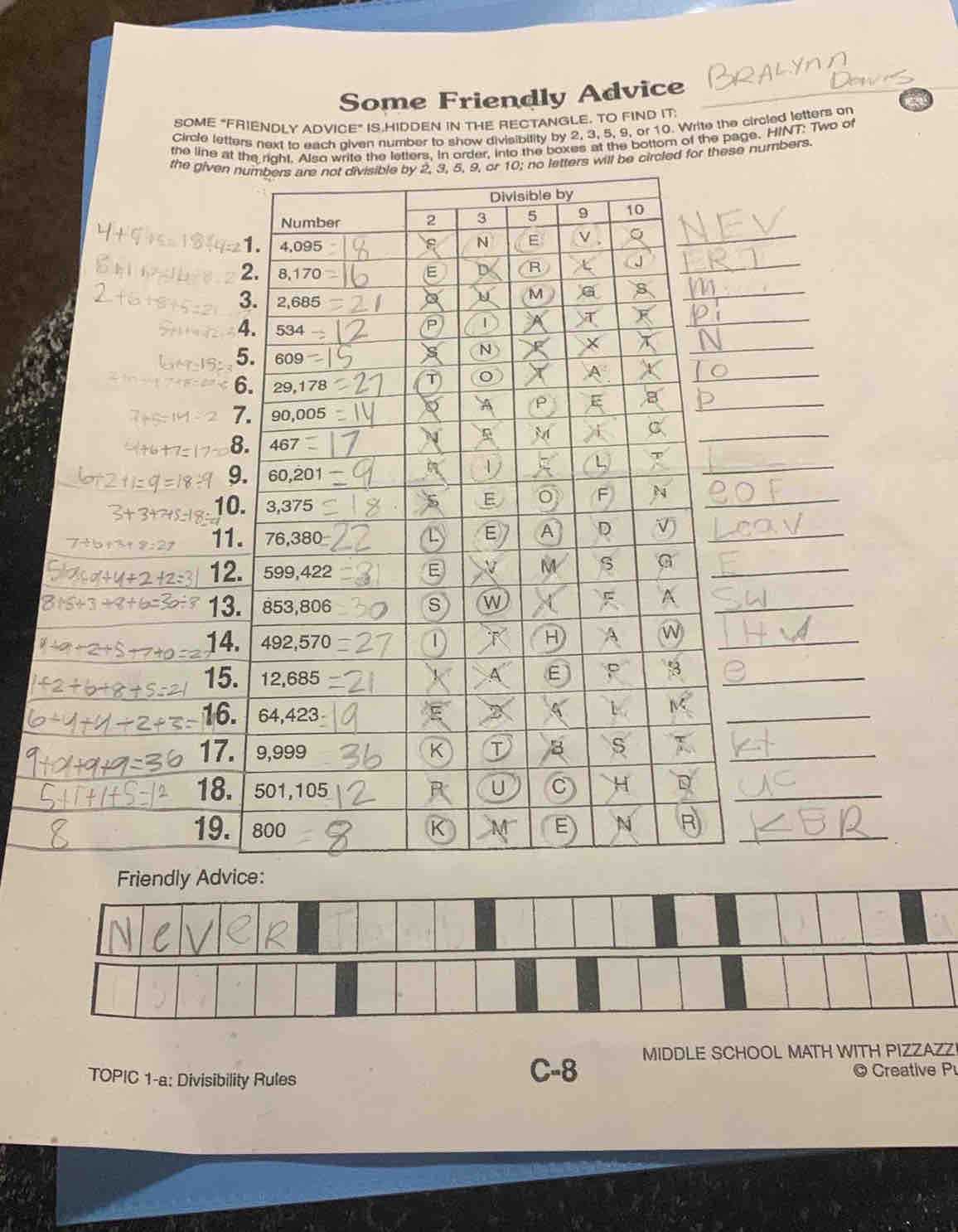
In this section, we focus on tackling a series of essential exercises designed to strengthen your understanding of fundamental mathematical principles. By breaking down each problem step by step, you’ll gain deeper insight into the core techniques needed for solving similar challenges in the future.
These exercises are crafted to guide you through various concepts, helping you build a solid foundation and improve your problem-solving abilities. The goal is to enhance your critical thinking skills, making it easier to approach more complex topics down the line.
As you work through each task, pay close attention to the methods and strategies used. Consistency and practice will be your best tools for mastering these concepts and advancing your skills.
Mathematical Solutions and Key Steps
This section covers a set of important exercises that aim to enhance your problem-solving abilities. By breaking down each challenge into clear, manageable steps, you will be able to master the essential techniques required to approach similar tasks with ease and confidence.
Each solution is designed to help you understand not just the steps involved, but also the reasoning behind each move. Focusing on developing a logical approach will enable you to handle more complex problems in the future, as the fundamental strategies remain the same.
By practicing these exercises, you will improve your ability to identify patterns, apply rules effectively, and solve mathematical problems more efficiently. The key to success is consistent practice and a clear understanding of the underlying methods.
Understanding the Concepts Behind Page 22
This section focuses on exploring the fundamental principles required to solve the exercises effectively. A clear understanding of the basic ideas will help you approach each problem logically and with greater confidence. Here, we break down the core techniques involved, ensuring a solid grasp of the material.
Key concepts to focus on include:
- Identifying patterns within the problems
- Understanding the rules that guide the solutions
- Breaking down complex tasks into smaller, simpler steps
- Applying the correct methods to each unique challenge
By internalizing these core strategies, you’ll develop the skills necessary to tackle similar problems independently. This approach allows for easier adaptation to more advanced topics as you continue your mathematical journey.
Key Steps to Solve Problems on Page 22
In this section, we break down the essential steps needed to tackle each problem effectively. By following a structured approach, you can ensure that you understand the process from start to finish. These steps help simplify complex challenges and lead to accurate solutions.
The process can be summarized as follows:
| Step | Description |
|---|---|
| Step 1 | Carefully read each problem and identify the key information. |
| Step 2 | Determine the method or formula needed to solve the problem. |
| Step 3 | Apply the chosen method to the given numbers or expressions. |
| Step 4 | Check your solution to ensure all steps are correctly followed. |
By following these steps, you’ll be able to approach each problem methodically and with greater clarity. Consistency in applying these techniques will lead to more efficient problem-solving and improved results.
How to Approach Algebraic Equations
Solving mathematical expressions requires a systematic approach to ensure that each element is understood and manipulated correctly. By following a structured method, you can simplify complex equations and find the solution step by step. Understanding the core principles behind these operations is essential for success.
The following table outlines the key steps to approach any given equation:
| Step | Action |
|---|---|
| Step 1 | Identify the variables and constants in the equation. |
| Step 2 | Isolate the variable by moving other terms to the opposite side. |
| Step 3 | Simplify both sides of the equation as much as possible. |
| Step 4 | Perform the necessary operations to solve for the unknown. |
| Step 5 | Double-check your solution by substituting it back into the original equation. |
By mastering these steps, you can approach each equation confidently and solve for the unknown in a logical manner. Regular practice will help improve your speed and accuracy over time.
Breaking Down Complex Math Problems
When faced with intricate mathematical challenges, the best approach is to simplify them into smaller, more manageable components. By breaking the problem into parts, you can address each section individually, making it easier to understand and solve the entire equation. This method helps clarify the process and reduces the feeling of being overwhelmed.
Identify Key Elements
The first step is to identify the important variables and constants within the problem. Determine what is given, what is unknown, and what needs to be calculated. Once you have a clear picture of the components involved, you can decide which operations are necessary to proceed.
Apply Step-by-Step Solutions
Next, approach the problem one step at a time. Start with the simplest operations and gradually move on to more complex ones. By breaking down the steps and performing them in sequence, you ensure accuracy and prevent mistakes. This methodical approach can be applied to any problem, no matter how complicated it appears at first glance.
Helpful Tips for Success
To excel in solving mathematical problems, it’s important to develop strategies that will guide you through each challenge. Effective preparation, attention to detail, and consistent practice can significantly improve your performance and confidence when tackling equations.
Here are some valuable tips to keep in mind:
- Understand the basic rules and concepts before attempting problems.
- Break down complex problems into simpler, smaller steps.
- Always double-check your calculations to avoid simple mistakes.
- Practice regularly to reinforce your understanding and improve speed.
- Use visual aids, like diagrams or charts, to clarify your thinking process.
- Don’t hesitate to ask for help if you’re stuck on a particular concept.
- Stay organized by writing out each step clearly and logically.
By following these strategies, you’ll improve your ability to solve problems more efficiently and achieve greater success in mathematical tasks. Remember, practice and persistence are key to mastering any topic.
Common Mistakes to Avoid in Math
When working through mathematical challenges, it’s easy to make mistakes that can lead to incorrect results. By being aware of common errors, you can avoid them and improve your problem-solving skills. Understanding the most frequent pitfalls is essential for achieving accurate solutions and building confidence in your abilities.
Typical Errors to Watch For
- Misunderstanding the problem’s requirements and skipping important details.
- Failing to follow the correct order of operations.
- Incorrectly simplifying or expanding expressions.
- Overlooking negative signs, especially when subtracting or dividing.
- Making arithmetic errors while performing basic calculations.
How to Prevent These Mistakes
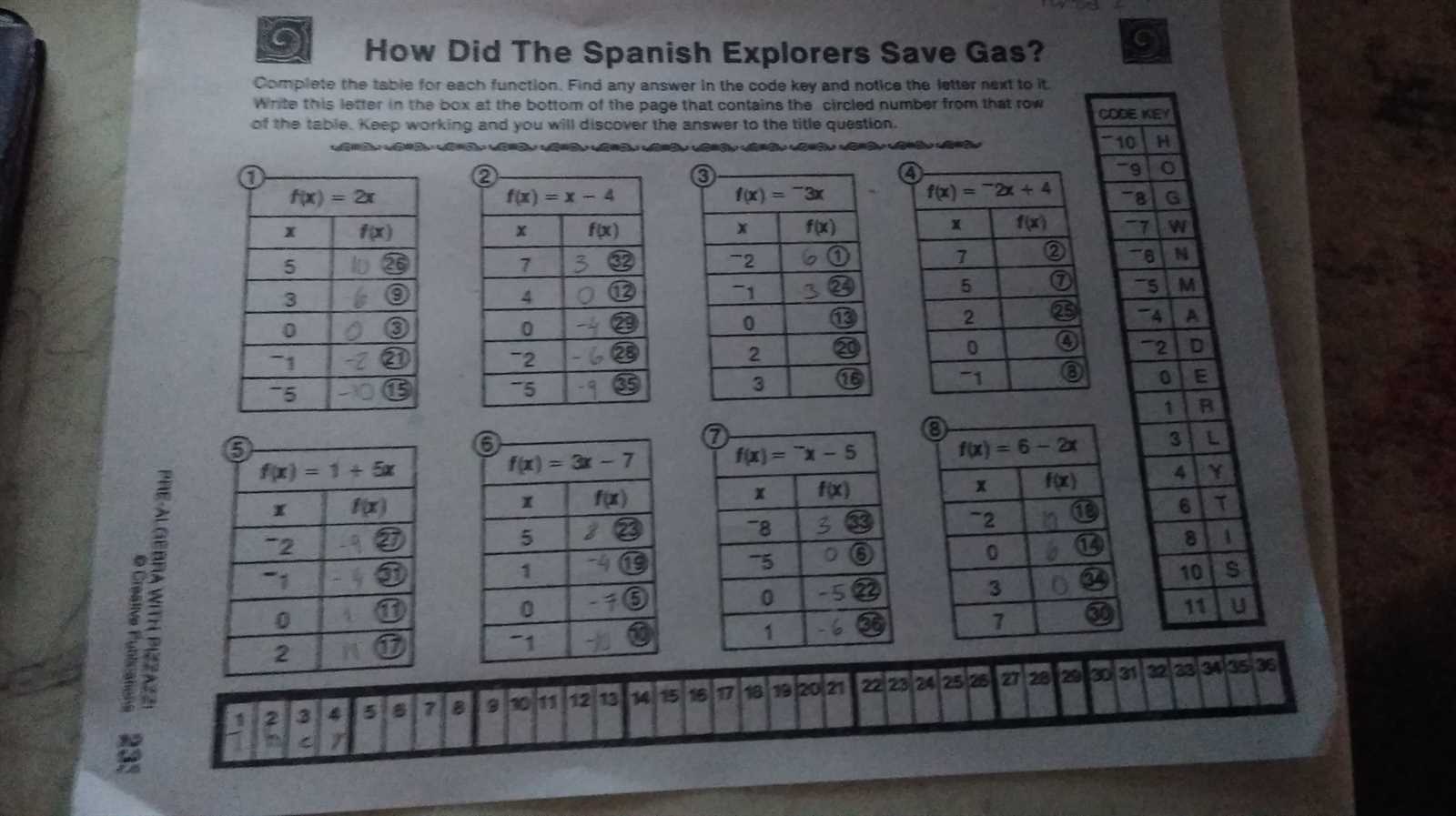
- Always read the problem carefully and highlight important values.
- Review the order of operations and apply it consistently.
- Double-check each step, especially when simplifying or combining terms.
- Keep track of signs throughout the process and verify your results.
- Use a calculator for complex calculations and verify the output.
By being mindful of these common errors and applying careful strategies, you can enhance your accuracy and become more proficient in solving mathematical problems.
Why Practice is Essential for Mastery
Achieving proficiency in solving mathematical problems requires consistent practice. Repetition helps reinforce concepts, enhances problem-solving abilities, and allows for the development of intuition over time. By practicing regularly, you build confidence and speed, which are crucial for mastering more advanced topics.
The Role of Repetition
Through repeated exposure to different types of problems, you become familiar with the patterns and techniques that make solving them easier. Regular practice enables you to internalize methods and perform them instinctively without having to think through each step in detail.
Building Confidence and Efficiency
When you practice regularly, you gain a deeper understanding of the material, which leads to greater confidence in your abilities. As you become more comfortable with various problem types, your efficiency increases, allowing you to solve problems faster and more accurately.
Strategies for Effective Problem Solving
To solve complex problems efficiently, it’s important to approach each task with a clear and structured strategy. By breaking down the process into manageable steps and using the right techniques, you can enhance your problem-solving skills and achieve accurate results more quickly.
Step-by-Step Approach
One of the most effective strategies is to approach the problem systematically. Begin by identifying what is known and what needs to be determined. Then, break the problem into smaller parts, addressing each one individually. This method allows you to focus on solving one step at a time, reducing confusion and improving clarity.
Use of Logical Reasoning
Logical reasoning is key to solving problems effectively. Try to think through the problem, considering all possible solutions and their consequences. Applying critical thinking will help you identify the most efficient method to solve each equation or situation, ensuring accuracy in the final result.
Exploring Different Mathematical Techniques
There are various methods and strategies that can be used to tackle mathematical problems effectively. Each technique offers unique advantages, depending on the type of problem at hand. Exploring different approaches allows you to choose the most suitable one, making the problem-solving process more efficient and accurate.
Substitution Method
The substitution method is a technique where one variable is solved in terms of another, allowing you to replace one equation with an equivalent expression. This method simplifies the system and makes it easier to solve for the unknowns. It is particularly useful when dealing with multiple variables and equations.
Factoring Technique
Factoring is another powerful tool in mathematics. By breaking down complex expressions into simpler factors, you can solve equations more easily. Factoring helps in identifying solutions for quadratic equations and other expressions, leading to a quicker and more straightforward resolution of problems.
Using Visual Aids for Better Understanding

Visual aids play an essential role in enhancing comprehension when solving mathematical problems. By representing abstract concepts with diagrams, charts, and graphs, these tools help clarify complex ideas and make them easier to grasp. They provide a concrete way to visualize relationships and patterns, leading to more effective problem-solving.
Benefits of Graphs and Diagrams

Graphs and diagrams offer a clear representation of mathematical relationships. They allow you to see trends, intersections, and key points, which might not be as obvious in written form. These visual tools are especially useful when working with equations or inequalities, as they help you understand the behavior of variables more intuitively.
Using Tables for Organization
Tables are excellent for organizing information systematically. They can be used to display values, compare different approaches, or track progress step by step. By organizing data visually, tables help to break down complex problems into simpler, more manageable pieces.
| Variable | Value | Step 1 | Step 2 |
|---|---|---|---|
| X | 5 | Substitute into equation | Solution: X = 5 |
| Y | 3 | Calculate value | Solution: Y = 3 |
By using visual aids like graphs, diagrams, and tables, you can gain a clearer and more organized view of the problem at hand. These tools simplify the process, helping you identify patterns, relationships, and solutions more efficiently.
Improving Your Mathematical Skills with Exercises

Regular practice through targeted exercises is one of the most effective ways to strengthen your problem-solving abilities. By consistently working through a variety of problems, you can reinforce key concepts, improve speed, and develop a deeper understanding of mathematical techniques. Whether you’re just starting or looking to refine your skills, exercises provide valuable opportunities for growth.
Key Benefits of Practice
- Reinforcement of Concepts: Repeated exposure to different types of problems helps solidify foundational knowledge and keeps important methods fresh in your mind.
- Increased Confidence: As you tackle more exercises, you gain confidence in your ability to approach and solve problems, reducing anxiety in higher-level challenges.
- Faster Problem-Solving: Regular practice increases your speed and efficiency, allowing you to solve problems more quickly and accurately.
Types of Exercises to Focus On
- Basic Operations: Mastering simple operations like addition, subtraction, multiplication, and division is essential for solving more complex problems.
- Word Problems: These exercises help improve your ability to interpret real-world scenarios and translate them into mathematical expressions.
- Advanced Techniques: As you progress, focusing on advanced exercises such as solving equations, graphing, and factoring will deepen your understanding and challenge your skills.
By regularly practicing exercises that target different aspects of mathematics, you’ll be well-equipped to approach any challenge with confidence and expertise.
The Role of Practice in Mastery

Consistent practice is a crucial element in achieving proficiency in any subject. It allows individuals to internalize concepts, improve their problem-solving speed, and develop a deeper understanding of the underlying principles. In the realm of mathematical studies, frequent engagement with various types of exercises is the key to mastering techniques and achieving long-term success.
By regularly working through problems, learners are able to solidify their grasp of methods and approaches, making them more efficient when faced with similar tasks. This repetition builds confidence and helps overcome challenges that might seem intimidating at first. Ultimately, practice is not just about completing exercises, but about strengthening the cognitive connections that allow for more fluid and intuitive problem solving.
The more time dedicated to practicing diverse scenarios, the more versatile and adaptable the learner becomes. Regular repetition also helps identify patterns and relationships between different concepts, which leads to faster and more accurate conclusions in future problems.
What to Do When You Get Stuck
Encountering obstacles during problem-solving is a common experience, but it doesn’t have to lead to frustration. When you find yourself unable to proceed, it’s important to remain calm and approach the challenge strategically. The key is to identify where you’re getting stuck and take steps to break the problem down into more manageable parts.
One effective method is to step away for a moment and return to the problem with a fresh perspective. Sometimes, taking a short break can help you see the solution in a new light. If you’re still struggling, try reviewing your previous steps to check for any errors or misunderstandings. Going over the problem from the start can help you identify any missteps that may have led to confusion.
Additionally, don’t hesitate to seek help if you’re stuck for an extended period. This could involve consulting a classmate, teacher, or online resource. Asking questions and discussing your approach with others can provide new insights or suggest different ways to approach the issue at hand.
Finally, practice patience. Some problems take time to understand and solve, and it’s okay to encounter difficulties along the way. By adopting a calm and methodical approach, you’ll be better equipped to tackle challenges and improve your overall problem-solving abilities.
Practical Applications of Mathematical Skills
Mathematical skills extend far beyond the classroom, playing a crucial role in a variety of real-world situations. Understanding how to manipulate numbers and solve equations is essential not just for academic success, but also for making informed decisions in everyday life. From budgeting to planning a trip, these skills help individuals navigate the complexities of daily tasks with greater precision and confidence.
One notable application is in the field of finance. Whether it’s managing personal expenses or understanding investments, mathematical reasoning allows people to calculate costs, evaluate risks, and plan for future needs. Skills such as calculating interest rates, understanding discounts, or determining loan payments are all rooted in basic mathematical principles.
Additionally, many professions, such as engineering, architecture, and technology, rely heavily on mathematical concepts to design, analyze, and solve complex problems. The ability to apply mathematical reasoning is crucial for creating efficient systems, structures, and devices that impact our daily lives. Even in fields like medicine, mathematics plays a key role in data analysis, diagnostics, and treatment planning.
By recognizing the practical applications of mathematical skills, individuals can better appreciate the value of their learning and see how these techniques contribute to success in both professional and personal endeavors.
How to Stay Motivated in Mathematics
Maintaining motivation when tackling complex mathematical problems can be challenging, especially when progress feels slow. However, there are several strategies that can help individuals stay engaged and continue pushing forward. Building a positive mindset and developing effective habits can make all the difference in mastering challenging concepts and overcoming obstacles.
One effective approach is to set small, achievable goals. Breaking down larger tasks into manageable chunks not only makes the process less overwhelming but also provides a sense of accomplishment as each goal is met. This can help maintain momentum and reinforce the belief that progress is being made, even when it feels like there is a long way to go.
Another helpful tactic is to mix up your study routine. Engaging with different types of problems, using various resources, and changing your study environment can keep the learning process fresh and stimulating. Sometimes, taking a short break or working through a problem with a different method can help reignite interest and offer new perspectives on the material.
Lastly, it’s essential to remind yourself of the long-term benefits of mastering these skills. Whether it’s the ability to solve practical problems, improve critical thinking, or advance academically, understanding the broader value of what you’re learning can provide the necessary motivation to keep going.
Advanced Techniques to Master Mathematics
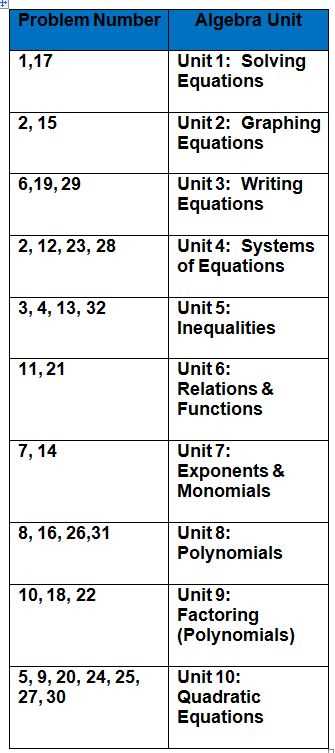
To truly excel in solving complex mathematical problems, it’s essential to go beyond basic strategies and delve into more advanced methods. These techniques not only enhance your problem-solving skills but also help you understand the deeper connections between various mathematical concepts. Mastery in this field requires a combination of creativity, logical thinking, and persistence.
One powerful technique is using substitution to simplify equations. By replacing variables with known values or expressions, you can transform complicated problems into simpler forms. This approach is particularly useful when dealing with systems of equations or when trying to find unknown values in more complex expressions.
Another effective strategy is factoring, which involves breaking down expressions into their constituent parts. This can help identify patterns and relationships that might otherwise be overlooked. Factoring is especially useful when solving quadratic equations or working with polynomial expressions.
Additionally, learning how to apply advanced methods such as graphing and working with matrices can give you a deeper understanding of mathematical functions. These tools allow you to visualize problems, recognize trends, and identify solutions that may not be immediately apparent.
- Substitution: Replacing variables to simplify and solve equations more efficiently.
- Factoring: Breaking down expressions to reveal hidden relationships and solutions.
- Graphing: Visualizing mathematical functions to better understand their behavior.
- Matrix Operations: Using matrices to solve complex systems and transformations.
By incorporating these advanced techniques into your practice, you can gain a more profound understanding of mathematical concepts and become adept at solving problems that might seem daunting at first glance.
Reviewing Solutions and Key Learnings

After completing a set of problems, it’s crucial to revisit the solutions and identify the main concepts that were applied throughout. This process helps solidify your understanding and enables you to recognize patterns that will be useful in tackling future challenges. A careful review not only clarifies any mistakes but also reinforces the steps and reasoning used to arrive at the correct answers.
Start by checking the final results against your expectations. If something seems off, go back and examine each step. Did you interpret the problem correctly? Were there any shortcuts you missed? Understanding where you went wrong is just as valuable as knowing the correct approach.
Key learnings from each problem can often be generalized to solve a variety of other issues. For example, if you used substitution to simplify an equation, this strategy can be applied to similar problems involving variables. The more you practice these methods, the more intuitive they become, allowing for quicker and more efficient solutions.
Remember that reviewing isn’t just about identifying mistakes–it’s about reinforcing successful strategies and understanding the logic behind them. This reflection is what leads to long-term mastery and confidence in problem-solving.