Understanding the fundamentals of mathematics is essential for tackling complex problems and improving critical thinking skills. The ability to break down intricate equations and identify solutions is a vital part of any academic journey. Whether you’re working through basic formulas or preparing for advanced exercises, grasping key principles can significantly enhance your problem-solving abilities.
Effective strategies and consistent practice play a crucial role in building confidence and mastering the material. With the right approach, challenging tasks can become more manageable, allowing learners to focus on developing a deeper understanding rather than simply memorizing rules. This guide will help you navigate through various techniques to achieve a clearer comprehension and stronger command over the concepts at hand.
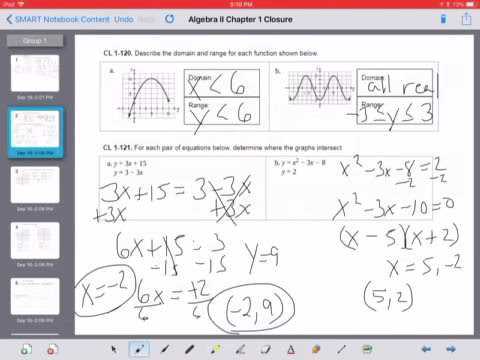
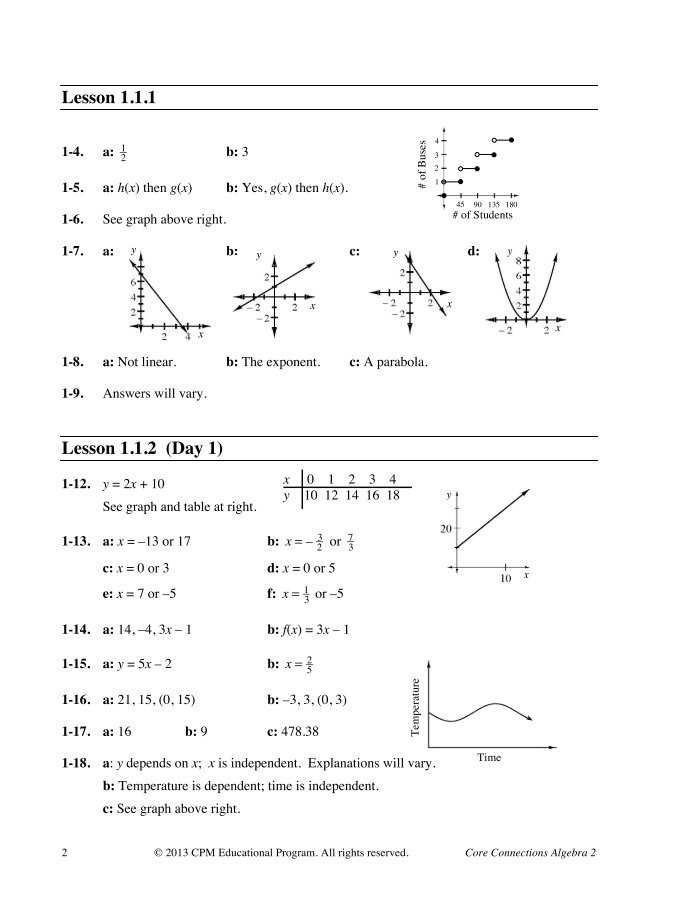
Core Connections Algebra Answers
Achieving success in mathematics requires a clear understanding of the principles and the ability to apply them effectively. When tackling various problems, it’s important to break down each step logically and systematically, ensuring that the foundational concepts are thoroughly grasped. This section provides insight into methods for solving complex exercises and offers helpful strategies to improve accuracy and speed.
Key Strategies for Solving Problems

- Start with simple examples to build confidence before advancing to more difficult tasks.
- Carefully read each question to ensure all parts are understood before proceeding.
- Identify patterns and relationships between variables that can simplify the process.
- Work through practice problems regularly to reinforce understanding and identify any gaps.
Common Challenges and How to Overcome Them
- Difficulty with word problems – Focus on breaking down the text into manageable parts and identify what is being asked.
- Confusion with formulas – Practice applying formulas in different contexts to increase familiarity and recall.
- Misinterpreting equations – Review the order of operations and pay attention to signs and coefficients.
Understanding Key Mathematical Concepts
Grasping the fundamentals of mathematical reasoning is essential for building a solid foundation in problem-solving. As you advance through more complex topics, understanding the core principles helps to break down challenges into simpler, manageable steps. By focusing on the relationships between numbers, variables, and equations, learners can enhance their ability to approach and solve a wide range of problems efficiently.
Building a Strong Mathematical Foundation
Before diving into advanced problems, it’s crucial to establish a clear understanding of basic concepts such as operations, variables, and equations. These form the building blocks for more sophisticated techniques and will be applicable in virtually every problem you encounter. Practicing basic exercises regularly will strengthen your ability to tackle more complex scenarios with confidence.
Approaching Complex Problems with Confidence
When faced with intricate equations or multi-step problems, breaking them down into smaller parts makes the process more manageable. Identify the given information, determine what needs to be solved, and apply the appropriate methods step by step. With consistent practice, complex tasks can be tackled with greater ease, and solutions can be found more quickly and accurately.
Solving Mathematical Problems Step by Step
Breaking down complex mathematical challenges into manageable steps is a crucial approach for mastering problem-solving techniques. By following a structured process, you can address each part of the equation methodically, reducing confusion and making it easier to reach the correct solution. This step-by-step strategy ensures that no important detail is overlooked and helps develop a deeper understanding of the problem at hand.
Step 1: Identify the Given Information
The first step in solving any problem is to carefully read through the question and identify all the known values. This can include numbers, variables, or specific conditions provided in the problem. Organize the information to clearly see what is given and what needs to be determined.
Step 2: Break the Problem into Smaller Parts

Next, divide the problem into smaller, more manageable sections. Identify the operations required and any relevant rules or formulas to apply. By working through each part of the problem separately, you can simplify the process and avoid feeling overwhelmed.
Tip: Always double-check the steps to ensure accuracy before moving on to the next part. Small errors can compound quickly, leading to incorrect results.
Common Mathematical Mistakes to Avoid
While working through mathematical problems, it’s easy to make mistakes that can lead to incorrect results. These errors often occur due to overlooking key steps, misunderstanding basic concepts, or rushing through calculations. By being mindful of these common pitfalls, you can significantly reduce mistakes and improve your accuracy when solving problems.
One frequent mistake is misapplying mathematical operations, such as incorrectly distributing a negative sign or failing to properly order operations. Another common error is overlooking the properties of exponents or forgetting to simplify expressions fully. By practicing careful attention to detail and reviewing your work at each step, you can avoid these common traps and build stronger problem-solving skills.
Key Concepts in Mathematical Problem Solving
Understanding the fundamental principles of mathematics is essential for effectively solving a wide range of problems. Mastering key concepts not only helps in performing calculations but also provides the foundation for tackling more complex challenges. Whether you are dealing with basic equations or exploring advanced topics, grasping these core ideas is crucial for success.
Essential Mathematical Principles
Several key concepts form the backbone of mathematical problem solving. These include understanding variables, operations, and equations, as well as how to manipulate and solve for unknowns. A solid grasp of these ideas allows for more efficient and accurate solutions.
Mathematical Operations and Techniques
Applying the correct operations is vital when working with equations. This includes addition, subtraction, multiplication, and division, as well as more advanced techniques like factoring or using the distributive property. Mastering these operations ensures a clearer understanding of more complex problems.
| Concept | Description |
|---|---|
| Variables | Symbols used to represent unknown values in an equation. |
| Operations | Basic arithmetic functions: addition, subtraction, multiplication, and division. |
| Equations | Mathematical statements that show the relationship between two expressions. |
| Factoring | Breaking down expressions into simpler parts, such as factoring a polynomial. |
Tips for Mastering Mathematical Techniques
Mastering mathematical techniques requires consistent practice, patience, and the ability to break down complex concepts into simpler steps. By applying the right strategies, you can improve your understanding and gain confidence when solving challenging problems. These tips will help guide you through the learning process and ensure you develop a solid grasp of essential methods.
| Tip | Description |
|---|---|
| Understand the Fundamentals | Ensure you have a strong grasp of basic concepts before advancing to more complex topics. |
| Practice Regularly | Repetition helps reinforce techniques and improve accuracy in solving problems. |
| Break Problems into Steps | Divide complex problems into smaller, manageable parts to reduce confusion. |
| Check Your Work | Always review your solutions to catch potential errors and ensure accuracy. |
| Learn from Mistakes | Understand where and why you made an error to prevent it from happening again. |
Tips for Mastering Mathematical Techniques
Mastering mathematical techniques requires consistent practice, patience, and the ability to break down complex concepts into simpler steps. By applying the right strategies, you can improve your understanding and gain confidence when solving challenging problems. These tips will help guide you through the learning process and ensure you develop a solid grasp of essential methods.
| Tip | Description |
|---|---|
| Understand the Fundamentals | Ensure you have a strong grasp of basic concepts before advancing to more complex topics. |
| Practice Regularly | Repetition helps reinforce techniques and improve accuracy in solving problems. |
| Break Problems into Steps | Divide complex problems into smaller, manageable parts to reduce confusion. |
| Check Your Work | Always review your solutions to catch potential errors and ensure accuracy. |
| Learn from Mistakes | Understand where and why you made an error to prevent it from happening again. |
Strategies for Improving Mathematical Skills
Enhancing your problem-solving abilities in mathematics requires a combination of understanding foundational concepts, practicing regularly, and applying different strategies to overcome challenges. By focusing on key areas and adopting effective techniques, you can sharpen your skills and become more confident in tackling complex problems. This section outlines practical strategies to help you improve your mathematical proficiency.
Practice Consistently
The most effective way to improve your skills is through consistent practice. The more problems you solve, the more familiar you become with different types of equations and techniques. Start with simpler problems and gradually move to more complex ones to build your confidence and mastery over time. Regular practice helps reinforce concepts and make them second nature.
Focus on Understanding, Not Memorizing
While memorization may help in the short term, understanding the reasoning behind each concept is essential for long-term success. Take the time to grasp why certain steps are taken and how different techniques work. This deeper understanding will allow you to adapt and apply your knowledge to a wide range of problems, rather than relying on rote memory.
Using Resources for Practice
To improve your problem-solving skills and gain a deeper understanding of mathematical concepts, it is important to use a variety of resources. These tools offer different types of exercises, explanations, and strategies that can enhance your practice. Whether you prefer digital platforms, textbooks, or worksheets, there are numerous options available to help you master key techniques and solve problems with greater confidence.
Types of Resources to Use
Different resources cater to different learning styles, making it essential to explore various options for effective practice. From interactive websites to practice books, choosing the right resources can significantly improve your comprehension and efficiency in solving problems.
| Resource Type | Benefits |
|---|---|
| Online Platforms | Interactive exercises with instant feedback, progress tracking, and a wide range of problem types. |
| Textbooks | Well-structured lessons and examples that provide step-by-step guidance for mastering concepts. |
| Worksheets | Printable exercises for focused practice on specific topics, perfect for reinforcing learning. |
| Tutoring Services | Personalized support with expert guidance, helpful for understanding difficult concepts and overcoming obstacles. |
Maximizing Resource Effectiveness
To make the most of these resources, it is important to approach them with a clear goal in mind. Set aside dedicated time for practice and focus on areas where you need the most improvement. Regularly revisiting challenging topics will help you reinforce your knowledge and gradually build confidence in your abilities.
Graphing in Mathematical Problem Solving
Graphing is a powerful tool in mathematics that allows you to visually represent relationships between variables. By plotting data points or equations on a coordinate plane, you can identify trends, intersections, and other key features that are often difficult to see through numbers alone. This method simplifies complex concepts and provides a clear visual understanding of mathematical problems.
Steps for Graphing Equations
Graphing involves several key steps that ensure accurate representation of equations or data. Whether you are working with linear equations, quadratic functions, or other mathematical expressions, following a structured approach will help you draw the graph correctly and interpret its meaning.
| Step | Description |
|---|---|
| 1. Identify the equation | Recognize the equation or function you need to graph and ensure it is in the correct form, such as slope-intercept or standard form. |
| 2. Find key points | Calculate critical points, such as the y-intercept or x-intercepts, which are essential for plotting the graph. |
| 3. Plot points on the coordinate plane | Place the points on the grid, carefully noting their positions on the x and y axes. |
| 4. Draw the curve or line | Connect the plotted points with a straight line or a smooth curve, depending on the type of equation. |
| 5. Analyze the graph | Examine the graph for key features like slopes, intercepts, and patterns that help in interpreting the equation’s behavior. |
Common Graphing Mistakes to Avoid
- Not labeling the axes or providing scale, which can lead to confusion in reading the graph.
- Forgetting to check the domain and range, which may cause incorrect or incomplete graphing.
- Plotting points inaccurately, especially when working with decimal values or fractional coordinates.
- Misinterpreting the slope or curvature of a graph, leading to incorrect conclusions.
Understanding Functions and Equations
Functions and equations are fundamental concepts in mathematics that form the foundation for solving a wide range of problems. A function describes a relationship between two sets of values, where each input corresponds to exactly one output. Equations, on the other hand, represent statements that show the equality of two expressions, often involving unknown variables. Mastering these concepts is essential for progressing in more advanced mathematical topics.
Key Concepts of Functions
Functions are a powerful way to express relationships between quantities. Understanding how to interpret and manipulate functions is crucial for solving equations and understanding real-world phenomena. Below are key aspects of functions:
- Domain and Range: The domain refers to all possible input values, while the range consists of all possible output values.
- One-to-One Functions: A function where each input has a unique output. This property is important for functions to be invertible.
- Function Notation: Functions are commonly written in the form f(x), where f represents the function, and x is the input.
- Graphing Functions: Functions can be represented visually on a coordinate plane, where the x-axis represents the input and the y-axis represents the output.
Understanding Equations
Equations are statements that show the equality of two expressions. Solving equations involves finding the values of unknown variables that satisfy the equality. Here are some key points to consider when working with equations:
- Linear Equations: Equations where the highest power of the variable is one. These equations represent straight lines when graphed.
- Quadratic Equations: Equations where the highest power of the variable is two. These represent parabolas when graphed.
- Systems of Equations: A set of two or more equations that share common variables. Solving the system involves finding the values that satisfy all equations simultaneously.
- Solving Strategies: Techniques such as substitution, elimination, and factoring can help solve equations, depending on the form of the equation.
Breaking Down Algebraic Expressions
Understanding and simplifying mathematical expressions is essential for solving problems efficiently. Breaking down complex expressions into simpler components allows for easier manipulation and solving. By recognizing patterns, factoring, and applying various techniques, you can gain a clearer understanding of how different parts of the expression relate to each other.
Identifying Terms and Coefficients
An expression consists of terms that are either constants or variables multiplied by coefficients. Breaking an expression into its individual parts can help identify its structure and simplify it. Here’s how you can approach this process:
- Variables: Letters that represent unknown values, such as x or y.
- Constants: Fixed values in the expression, such as 5 or -3.
- Coefficients: Numbers that multiply the variables, like the 3 in 3x.
- Operators: Symbols that indicate operations, such as addition, subtraction, multiplication, or division.
Simplifying Expressions
Once the terms, coefficients, and variables are identified, the next step is simplifying the expression. This can be done by combining like terms, applying distributive properties, or factoring.
- Combining Like Terms: Combine terms with the same variable and exponent. For example, 3x + 5x simplifies to 8x.
- Distributive Property: Use the distributive property to expand expressions, such as a(b + c) = ab + ac.
- Factoring: Factor expressions by finding common factors, such as factoring x^2 + 5x + 6 into (x + 2)(x + 3).
Real-Life Applications of Algebra
Mathematics is not just a theoretical subject; it has practical applications in many fields of daily life. By understanding the relationships between variables and how they change, we can solve real-world problems. Whether managing finances, designing buildings, or analyzing trends, mathematical principles help to make informed decisions and improve outcomes. In this section, we will explore how mathematical concepts are applied in everyday situations.
Finance and Budgeting
One of the most common uses of mathematical concepts is in managing personal or business finances. Algebraic methods can help individuals and organizations track expenses, calculate savings, and plan future investments.
- Budgeting: Creating a budget involves using equations to allocate a fixed amount of money across various expenses and savings goals.
- Loan Repayments: Understanding interest rates and calculating loan payments are often done using formulas based on algebraic expressions.
- Investment Growth: Algebra is used to predict how investments will grow over time, considering factors such as compound interest.
Engineering and Architecture
In fields such as engineering and architecture, mathematical models and equations are essential for designing structures, systems, and products. These applications often involve complex calculations that are simplified using algebraic techniques.
- Structural Design: Engineers use algebra to calculate the forces acting on buildings and bridges to ensure they are stable and safe.
- Material Requirements: Architects apply algebra to determine the amount of materials needed for construction based on dimensions and the project’s scope.
- Optimization: Algebraic methods are used to optimize designs for cost, efficiency, and durability in both construction and manufacturing.
Health and Medicine
Algebra is also widely used in healthcare and medicine for tasks ranging from dosage calculations to data analysis in medical research.
- Dosage Calculations: Doctors and pharmacists use algebra to calculate the correct dosage of medications based on a patient’s weight and age.
- Medical Data Analysis: Algebraic models are used to analyze patient data, helping doctors make decisions about treatment plans.
- Medical Imaging: Techniques such as MRI and CT scans rely on mathematical algorithms to create images of the inside of the body.
Exam Preparation for Algebra Tests
Preparing for mathematics exams requires a strategic approach that includes reviewing key concepts, practicing problem-solving, and understanding the exam format. The goal is not only to memorize formulas but also to develop a deep understanding of how mathematical principles work. In this section, we will explore effective strategies for studying and excelling in mathematics assessments.
Understanding the Topics
Before you start revising, it’s important to know which topics will be covered in the exam. Make a list of the key areas you need to focus on and ensure you are familiar with all the relevant concepts.
- Key Equations and Formulas: Make sure you understand and can apply all the essential formulas, such as solving for variables and simplifying expressions.
- Concepts and Procedures: Practice solving problems step by step, ensuring that you are comfortable with the procedures for solving equations, working with inequalities, and graphing functions.
- Real-World Applications: Recognize how the mathematical principles you have learned can be applied to practical situations, as this often forms part of exam questions.
Practice and Problem Solving
The most effective way to prepare for a math exam is through consistent practice. This helps reinforce your understanding and improve your speed and accuracy during the test.
- Sample Problems: Work through past exam papers and practice problems to familiarize yourself with the types of questions that are typically asked.
- Timed Practice: Simulate exam conditions by timing yourself as you solve problems. This will help you manage your time effectively during the actual test.
- Focus on Weak Areas: Identify the areas where you struggle the most and allocate more time to practicing those topics. Seek help if needed from a tutor, peer, or online resources.
Effective Revision Techniques
Effective revision is about more than just reading your notes. Active learning strategies will help reinforce your understanding and retention of the material.
- Flashcards: Create flashcards for key concepts, formulas, and definitions. These can be a quick and efficient way to test your memory.
- Study Groups: Join a study group to discuss and solve problems together. Explaining concepts to others can deepen your own understanding.
- Online Resources: Utilize online platforms that offer practice tests, instructional videos, and interactive problem-solving tools.
Test-Taking Strategies
On the day of the exam, staying calm and focused is essential for performing well. Consider these strategies for approaching the test.
- Read Carefully: Take the time to read each question thoroughly before attempting an answer. This ensures you understand exactly what is being asked.
- Start with Easier Problems: Begin with
How to Work with Variables
Working with variables is a fundamental aspect of mathematics that involves manipulating symbols to represent unknown values. These symbols, often letters, allow us to express general relationships, formulate equations, and solve problems where specific numbers are not initially known. In this section, we will explore essential techniques for working with variables, helping you understand how to effectively handle them in various mathematical contexts.
Understanding the Role of Variables
Variables can represent numbers in equations, allowing us to generalize problems and find solutions for various situations. The first step is to understand that a variable can take any value within a given set. It can stand for a constant or change depending on the context.
- Substitution: You can substitute a specific value for a variable when solving equations or problems. For example, if you know that x = 5, you can replace x with 5 in any expression or equation.
- Solving for Variables: Often, you’ll be tasked with finding the value of a variable. This involves isolating the variable on one side of the equation using mathematical operations.
- Using Variables in Real-Life Problems: Variables are not just confined to math problems; they are used to model situations like budgeting, distance, time, and many other real-world applications.
Techniques for Manipulating Variables
To work with variables efficiently, it’s essential to understand a few key techniques for simplifying expressions and solving equations. These skills will help you approach more complex problems with ease.
- Combining Like Terms: When you have similar terms in an expression, such as 3x and 5x, you can combine them to simplify the expression. In this case, 3x + 5x becomes 8x.
- Balancing Equations: To solve for a variable, you need to maintain equality on both sides of the equation. Apply the same operation to both sides to isolate the variable.
- Factorization: Sometimes, expressing an equation in factored form can make solving easier. This technique involves rewriting expressions as products of their factors.
Common Core Standards and Algebra
The framework for understanding and mastering mathematical concepts is grounded in clear guidelines that help students progress through essential skills. These guidelines focus on providing a structured approach to various mathematical topics, ensuring that learners build a solid foundation for problem-solving. In this section, we explore how these educational standards guide the learning process for mathematical topics, particularly in areas related to solving equations and working with variables.
Understanding the Importance of Standards in Math
The standards set forth by educational frameworks play a crucial role in ensuring consistency and depth in the way mathematics is taught. These standards ensure that students gain a comprehensive understanding of essential mathematical concepts, providing the tools needed for future academic success and real-world problem-solving.
- Structured Learning Pathways: The standards outline a clear pathway for learning, ensuring that students develop skills in a logical progression. Starting with foundational concepts, they build up to more complex problems involving equations and functions.
- Application of Knowledge: These guidelines emphasize the importance of not just solving problems but also applying mathematical knowledge to real-life situations. By doing so, students are better prepared for both academic challenges and everyday problem-solving.
- Assessment of Proficiency: The standards also provide a way to measure progress and proficiency in mathematical skills, helping teachers assess whether students are mastering the concepts needed for further study.
Key Concepts in the Standards for Mathematics
The standards provide a focus on several key concepts, which are essential for developing a strong mathematical skill set. Some of the primary areas of focus include:
- Equations and Inequalities: Students are expected to understand the properties of equations and inequalities and be able to solve them using various methods. This includes understanding how to isolate variables and apply different mathematical operations.
- Functions and Relationships: A significant emphasis is placed on understanding the relationships between variables, graphing functions, and recognizing patterns. This helps students visualize how mathematical expressions behave.
- Problem-Solving Strategies: The standards encourage the development of effective problem-solving techniques, including breaking down complex problems into smaller, more manageable steps and using logical reasoning to find solutions.
Improving Problem-Solving Abilities
Enhancing your ability to solve mathematical problems effectively is a crucial skill that can be developed through practice and strategic approaches. In this section, we focus on techniques that help sharpen your reasoning and increase your confidence in tackling various challenges. With the right mindset and tools, you can improve your problem-solving capabilities and approach any task with a clearer perspective.
Strategies for Effective Problem Solving
To become more proficient in solving problems, it’s important to adopt certain strategies that break down complex situations into manageable steps. These strategies help in organizing your thoughts and making logical decisions that lead to accurate solutions.
- Understand the Problem: Take time to carefully read and analyze the problem. Break it down into smaller parts and identify the given information, what’s being asked, and any constraints that apply.
- Develop a Plan: Once you understand the problem, think about the methods or formulas you can use to solve it. Whether it’s using algebraic operations or geometric principles, creating a clear plan is essential.
- Work Step by Step: Avoid rushing through the process. Take it step by step, ensuring each part of the calculation or reasoning is correct before moving on to the next. This approach helps prevent errors and reinforces understanding.
- Check Your Work: After finding a solution, review your steps to ensure there are no mistakes. Double-checking your calculations and logic is a key step in confirming the accuracy of your results.
Building Confidence Through Practice
Consistent practice is one of the most effective ways to build confidence and improve your problem-solving skills. By working on a variety of problems, you can reinforce your understanding of different concepts and techniques.
- Start with Simple Problems: Begin with problems that are easy to understand, then gradually increase the difficulty as your skills improve. This will build confidence and help you apply what you’ve learned to more complex tasks.
- Seek Feedback: Don’t hesitate to ask for help or feedback when you’re unsure. Learning from mistakes and discussing problems with others can offer new insights and help you grow as a problem solver.
- Keep Practicing Regularly: Consistency is key. Set aside time each day or week to practice problem-solving. The more you practice, the better you will get at recognizing patterns and solving problems quickly and accurately.