
In this section, we explore various methods and techniques to tackle a range of mathematical problems. Understanding the underlying concepts and applying step-by-step strategies are essential for mastering complex equations and expressions.
By focusing on key problem-solving approaches, we aim to simplify the process and guide you through each task effectively. Whether you’re grappling with linear equations or interpreting real-world scenarios, the skills gained here will empower you to approach problems with greater clarity and precision.
Clear explanations and practical examples will support your journey through the material, providing you with the tools to succeed in both exercises and assessments. By the end of this section, you will be equipped with the knowledge to handle challenging problems confidently and accurately.
Mathematical Solutions and Techniques for Success
In this section, we delve into solving essential mathematical exercises designed to sharpen problem-solving skills. The focus is on applying various methods to simplify expressions, solve equations, and understand key concepts that form the foundation of advanced mathematical tasks.
Key Problem-Solving Strategies
Mastering mathematical challenges requires familiarity with several effective strategies. Here are some crucial techniques:
- Step-by-step approach: Breaking down complex problems into smaller, manageable parts.
- Identifying patterns: Recognizing recurring structures to simplify solutions.
- Checking work: Verifying solutions by substitution or alternative methods.
- Graphical representation: Using graphs to visualize relationships and solutions.
Common Problem Types and Solutions
Several problem types are frequently encountered and require specific methods for efficient resolution. Here are some examples:
- Linear Equations: Solve using substitution or elimination techniques.
- Systems of Equations: Approach by graphing or using matrix methods for more complex scenarios.
- Word Problems: Translate verbal information into mathematical expressions and solve accordingly.
Applying these strategies will allow for a deeper understanding of each problem type and lead to accurate, reliable results in every task encountered.
Overview of Chapter 2 Concepts
This section introduces the key principles and techniques necessary to solve various types of mathematical problems. By understanding these core ideas, you will develop the skills needed to approach equations, expressions, and real-world scenarios effectively.
Understanding Basic Mathematical Operations
The foundation of this material revolves around mastering the core operations and their applications in problem-solving. These concepts will help you simplify complex expressions and solve for unknowns.
- Adding and subtracting: Mastering these operations to manipulate and simplify algebraic expressions.
- Multiplying and dividing: Using multiplication and division to solve equations and determine relationships between variables.
Solving Equations and Expressions
Another major aspect of this section is solving for variables in different mathematical contexts. Whether you’re working with simple or complex expressions, the ability to isolate variables and solve equations is crucial.
- Linear equations: Finding the value of variables by balancing both sides of the equation.
- Word problems: Translating real-world situations into mathematical models and solving for unknowns.
By gaining a deeper understanding of these concepts, you’ll be equipped with the necessary tools to tackle a wide range of mathematical challenges.
Key Strategies for Solving Problems
Effective problem-solving in mathematics requires a systematic approach to ensure accuracy and efficiency. By applying the right strategies, you can simplify complex tasks, identify patterns, and ultimately find solutions with ease. Below are several essential strategies to help guide you through various problems.
| Strategy | Description |
|---|---|
| Understand the problem | Read the problem carefully, ensuring you identify all given information and what needs to be solved. |
| Break it down | Divide the problem into smaller, more manageable parts to tackle each step-by-step. |
| Use diagrams or graphs | Visual representations can often make complex relationships easier to understand and solve. |
| Choose the right method | Determine which mathematical operation or technique is best suited for solving the problem at hand. |
| Check your work | After solving, review your steps and solutions to ensure there are no errors. |
By consistently applying these strategies, you’ll be able to approach any problem with greater confidence and precision, leading to more successful solutions in a variety of mathematical scenarios.
Step-by-Step Solutions to Exercises
This section will guide you through a series of problems with detailed, step-by-step explanations. By breaking down each task into smaller, manageable parts, you can learn how to approach complex problems systematically and solve them with confidence.
Solving Linear Equations
Let’s walk through the process of solving a simple linear equation. Follow these steps to isolate the variable and find the solution:
- Identify the equation: Write down the equation you need to solve.
- Move like terms: Combine terms on both sides to simplify the equation.
- Isolate the variable: Use addition or subtraction to isolate the variable on one side of the equation.
- Solve: Use multiplication or division to solve for the variable.
- Check your solution: Substitute the solution back into the original equation to verify.
Solving Word Problems
Word problems often involve translating real-world scenarios into mathematical expressions. Here’s how to approach them:
- Read carefully: Understand the problem fully before attempting a solution.
- Define variables: Assign variables to represent unknown quantities.
- Translate to equations: Convert the information given into a mathematical equation.
- Solve: Apply appropriate methods to find the values of the variables.
- Verify: Check if the solution makes sense in the context of the problem.
By practicing these methods, you’ll improve your ability to solve various types of problems, building a strong foundation for more advanced concepts.
Understanding Variables and Expressions
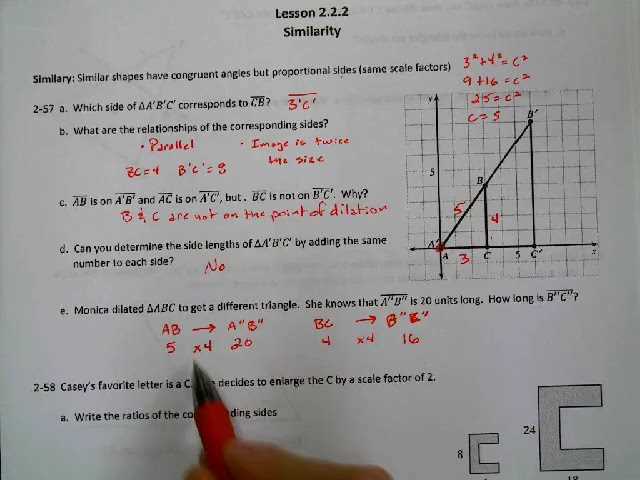
In mathematics, understanding the relationship between variables and expressions is key to solving problems efficiently. Variables act as placeholders for unknown values, while expressions represent mathematical operations involving numbers and variables. Mastering these concepts helps simplify complex problems and makes it easier to find solutions.
What are Variables?
Variables are symbols, usually letters, that represent unknown or changing quantities. They allow us to write generalized equations and make statements about relationships between different values. For example, in the equation “x + 5 = 10,” the letter “x” is the variable, and it represents a number that we need to determine.
- Common variables: Often, variables are represented by letters such as x, y, or z.
- Use in equations: Variables are used to create equations that describe relationships or patterns in mathematical problems.
What are Expressions?
Expressions are combinations of numbers, variables, and mathematical operations such as addition, subtraction, multiplication, and division. An expression does not contain an equality sign, unlike an equation. For example, “3x + 4” is an expression where 3 is multiplied by the variable “x” and 4 is added to the result.
- Types of expressions: Expressions can be simple (like “2x + 5”) or more complex, involving multiple operations.
- Simplification: Simplifying expressions involves combining like terms to make them easier to work with.
Understanding variables and expressions provides the foundation for more advanced mathematical topics. With practice, you’ll be able to recognize how these elements work together to form equations that lead to solutions.
Breaking Down Linear Equations
Solving linear equations requires breaking them down into simpler steps to isolate the variable and find its value. The process involves applying basic mathematical operations to both sides of the equation, maintaining balance, and carefully simplifying the terms. By understanding the structure of these equations, you can solve them with confidence and accuracy.
Step-by-Step Process

Here’s a clear breakdown of how to approach a linear equation:
- Identify the equation: Start by writing the equation and determining what you need to solve for.
- Combine like terms: Simplify both sides by adding or subtracting terms that are the same.
- Isolate the variable: Use addition or subtraction to move terms containing the variable to one side of the equation.
- Solve for the variable: Use multiplication or division to solve for the variable.
- Check your solution: Substitute the solution back into the original equation to verify it’s correct.
Example of Solving a Linear Equation
Consider the equation 2x + 5 = 15. Let’s solve it step-by-step:
- Step 1: Subtract 5 from both sides: 2x = 10.
- Step 2: Divide both sides by 2: x = 5.
- Step 3: Check the solution by substituting x = 5 into the original equation: 2(5) + 5 = 15, which is correct.
By following these steps, you can solve any linear equation efficiently and accurately.
Graphing Techniques for Algebraic Problems
Graphing is a powerful tool for visualizing mathematical relationships and solving problems. By plotting equations on a coordinate plane, you can better understand the behavior of functions, identify solutions, and recognize patterns. The process of graphing helps transform abstract concepts into tangible visual representations, making it easier to interpret and analyze data.
Basic Steps for Graphing Equations
To graph an equation, follow these fundamental steps:
- Identify the equation: Write down the equation you need to graph and make sure it’s in a solvable form.
- Find key points: Calculate values of the variable to plot key points on the graph. This often involves substituting specific values into the equation.
- Plot the points: Mark the points on the coordinate plane. Each point represents a solution to the equation.
- Connect the points: Draw a line or curve through the points to complete the graph, depending on the type of equation.
Graphing Linear Equations

Graphing linear equations involves plotting straight lines that represent relationships between two variables. Here’s how to approach graphing a linear equation like y = 2x + 3:
- Step 1: Choose several values for x (e.g., x = -2, 0, 2) and solve for y to find corresponding points.
- Step 2: Plot the points (x, y) on the coordinate plane.
- Step 3: Draw a straight line that passes through all the points.
Graphing provides a clear visual representation of the solutions and the relationship between variables, helping to confirm your answers and improve understanding.
Working with Systems of Equations
When solving multiple equations involving two or more variables, the goal is to find a set of values that satisfy all the equations simultaneously. Systems of equations often arise in real-life problems where multiple relationships need to be solved together. By using different methods, you can determine the values that solve the system as a whole.
Methods for Solving Systems
There are several common approaches for solving systems of equations, each useful depending on the structure of the problem:
- Substitution Method: Solve one equation for one variable and substitute that expression into the other equation to find the values of both variables.
- Elimination Method: Add or subtract equations to eliminate one variable, allowing you to solve for the remaining variable.
- Graphical Method: Plot both equations on a coordinate plane and find the point where the lines intersect, which represents the solution.
Example: Solving Using Substitution
Consider the following system of equations:
- 2x + y = 10
- x – y = 2
To solve using substitution, follow these steps:
- From the second equation, solve for one variable, say y = x – 2.
- Substitute y = x – 2 into the first equation: 2x + (x – 2) = 10.
- Simplify and solve for x: 3x – 2 = 10, so x = 4.
- Substitute x = 4 back into y = x – 2 to find y: y = 4 – 2 = 2.
The solution to the system is x = 4 and y = 2. Systems of equations can be solved using similar steps, allowing for a clear and accurate solution for complex problems.
Solving Word Problems in Algebra
Word problems provide a real-world context for mathematical concepts, requiring you to translate a written description into mathematical expressions and equations. By breaking down the problem into smaller, manageable steps, you can identify the relationships between variables and find solutions effectively. Understanding the structure of word problems is key to applying the right methods and solving them correctly.
Steps to Solve Word Problems
Follow these essential steps to approach word problems systematically:
- Read the problem carefully: Understand what is being asked and identify the important information given in the problem.
- Define the variables: Assign a variable to represent the unknown quantities in the problem.
- Set up an equation: Translate the relationships and conditions described in the problem into a mathematical equation.
- Solve the equation: Use appropriate techniques, such as substitution or elimination, to find the values of the variables.
- Check your answer: Substitute the solution back into the context of the problem to ensure it makes sense.
Example: Solving a Word Problem
Here’s an example of how to approach a simple word problem:
Problem: A total of 40 students are attending a school play. The number of students who purchased tickets for the play is twice the number of students who volunteered to help. How many students volunteered to help?
Solution:
- Let the number of students who volunteered be represented by x>.
- The number of students who purchased tickets is twice the number who volunteered, so it is 2x>.
- Now, set up an equation: x + 2x = 40.
- Simplify: 3x = 40.
- Solve for x: x = 40 ? 3 = 13.33.
Since the result is not a whole number, this problem may have been worded or calculated incorrectly. Always check your calculations and assumptions to ensure that they make sense in the real-world context of the problem.
By breaking down the problem and applying these steps, you can tackle word problems in a logical and organized way.
Common Mistakes to Avoid in Algebra
When working with mathematical equations and expressions, it’s easy to make errors that can lead to incorrect solutions. Understanding the most frequent mistakes and learning how to avoid them is crucial to mastering the material. These errors often stem from misinterpreting operations, forgetting rules, or skipping key steps. Being aware of these common pitfalls can help ensure more accurate results.
Frequent Errors and How to Prevent Them
Here are some of the most common mistakes made when solving equations, along with tips to avoid them:
| Mistake | How to Avoid It |
|---|---|
| Misunderstanding the distributive property | Ensure to distribute terms correctly. For example, in a(b + c) = ab + ac, make sure you multiply each term inside the parentheses by the factor outside. |
| Forgetting to reverse the inequality sign when multiplying/dividing by a negative | Remember, when multiplying or dividing an inequality by a negative number, flip the inequality sign. For example, -2x > 6 becomes x . |
| Dropping negative signs | Pay attention to signs, especially when dealing with subtraction or negative numbers. For example, -5 + (-2) is not the same as -5 – 2. |
| Not checking the solution | After solving an equation, always substitute the solution back into the original equation to verify the result. |
Tips for Successful Problem Solving
To avoid these and other mistakes, here are a few helpful tips:
- Double-check your steps: Carefully review each step in your calculations to ensure nothing is skipped or miscalculated.
- Stay organized: Keep equations and terms clear to avoid confusion, especially with complex expressions.
- Practice regularly: The more you practice, the better you will become at spotting and preventing common mistakes.
By being mindful of these errors and following these strategies, you can improve your problem-solving skills and avoid common pitfalls.
Helpful Tips for Algebraic Success
Mastering mathematical concepts can often seem challenging, but with the right strategies, success is achievable. By following a few practical tips and maintaining a consistent approach, you can enhance your understanding and improve your problem-solving abilities. This section outlines essential advice to help you excel in mathematical problem-solving and develop a deeper grasp of key concepts.
Focus on Understanding, Not Just Memorization
While memorizing formulas and procedures is important, true success comes from understanding the reasoning behind them. Try to grasp the “why” behind each operation or rule, rather than just memorizing steps. This deeper understanding allows you to apply the concepts flexibly to a variety of problems.
Practice Regularly and Consistently
Repetition is key when it comes to mastering any skill, and mathematics is no exception. Regular practice helps solidify concepts in your memory and makes it easier to recall them when solving more complex problems. Working through different types of problems will also help you develop a versatile problem-solving toolkit.
- Work on a variety of problems: Don’t just stick to one type of problem. Challenge yourself with problems of varying difficulty to strengthen your skills.
- Take your time: Avoid rushing through problems. Spend time carefully considering each step, and double-check your work to ensure accuracy.
- Seek help when needed: If a concept is unclear, don’t hesitate to ask for help. Whether it’s a teacher, a tutor, or online resources, seeking clarification will prevent misunderstandings from building up.
By adopting these strategies and committing to consistent practice, you’ll be well on your way to mastering mathematical concepts and solving problems with confidence.
Practice Problems to Reinforce Learning

Regular practice is essential to mastering any skill, especially in mathematical problem solving. By tackling a variety of exercises, you can reinforce the concepts you’ve learned and ensure a deeper understanding. Working through practice problems not only helps you apply what you’ve studied but also allows you to identify areas that may need further attention. Here are some exercises designed to strengthen your grasp of key mathematical principles.
Types of Practice Problems
Below are different types of problems that will help solidify your knowledge and improve your problem-solving skills:
| Problem Type | Example |
|---|---|
| Solving Basic Equations | Solve for x: 3x + 4 = 19 |
| Working with Expressions | Simplify: 5x + 3x – 2 |
| Graphing Linear Functions | Plot the graph of y = 2x + 1 |
| Word Problems | A store sells pencils for $1.50 each. Write an equation for the total cost of x pencils. |
Steps for Effective Practice

To get the most out of your practice sessions, follow these steps:
- Start with simpler problems: Begin with basic exercises to build confidence before moving on to more complex challenges.
- Take your time: Carefully analyze each problem, making sure you understand the steps involved before moving forward.
- Review solutions: After completing each problem, review the solution to ensure you didn’t make any mistakes and fully understand the reasoning behind it.
- Gradually increase difficulty: As you become more comfortable with simpler problems, increase the difficulty to challenge yourself and improve your skills.
By practicing these problems regularly, you will strengthen your understanding of mathematical concepts and develop the skills needed to solve more complex problems with ease.
Real-World Applications of Algebra
Mathematical principles are not confined to textbooks; they play a crucial role in a wide range of real-world scenarios. Understanding how to manipulate variables and solve equations can help in making informed decisions, solving practical problems, and even predicting future outcomes. Whether in business, engineering, or everyday life, the ability to apply mathematical concepts is invaluable. Below are some key areas where these concepts are commonly used.
One of the most important areas where mathematical problem-solving comes into play is in financial planning. From calculating interest rates on loans to determining monthly payments, mathematical skills help individuals and businesses make sound financial decisions. Similarly, architects and engineers rely on mathematical models to design structures that are both functional and safe, taking into account various factors like materials and weight distribution.
In addition, technology and computer science also depend heavily on mathematical equations. Algorithms, which are used in everything from search engines to artificial intelligence, are based on mathematical principles. Even in fields such as medicine, math is used to interpret data, model disease spread, and create treatment plans.
Understanding the real-world applications of math not only strengthens your problem-solving abilities but also enhances your ability to think critically about the world around you. By seeing how equations and models are used in various industries, you can better appreciate the value of mastering these skills.
Reviewing Key Algebraic Terms
Understanding the fundamental terms and concepts is crucial for success in any mathematical field. These terms form the foundation upon which more complex ideas are built. Having a clear grasp of these basic elements enables individuals to approach problems confidently and develop problem-solving strategies. Below are some of the essential terms that are commonly encountered when working with mathematical expressions and equations.
- Variable: A symbol, typically a letter, used to represent an unknown value in an equation or expression. Common variables include x, y, and z.
- Expression: A mathematical phrase that can contain numbers, variables, and operations, but does not have an equality sign. For example, 3x + 5.
- Equation: A statement that two expressions are equal, often containing one or more variables. An example is 2x + 3 = 7.
- Coefficient: A numerical value that multiplies a variable. In the expression 4x, 4 is the coefficient of x.
- Constant: A fixed value that does not change. In the expression 5x + 3, 3 is the constant.
- Solution: The value(s) of the variable that make an equation true. For example, in the equation x + 2 = 5, the solution is x = 3.
- Term: A single mathematical element, which could be a number, a variable, or a combination of both, such as 3x or 7.
By familiarizing yourself with these fundamental terms, you will improve your understanding of more complex concepts and be better equipped to tackle various mathematical problems. Mastery of the language of mathematics helps pave the way for success in problem-solving tasks.
Approaching Algebra with Confidence
Success in mathematics often begins with the right mindset. Approaching problems with confidence allows individuals to break down complex tasks into manageable steps. The key to developing this confidence lies in understanding the core principles and building on them gradually. With practice, anyone can improve their ability to solve mathematical problems and navigate through challenges with ease.
One of the most important strategies is to maintain a positive attitude, especially when faced with difficult problems. Recognize that mistakes are a natural part of the learning process and that each error presents an opportunity to gain deeper insight into the material. The more you engage with problems, the more familiar you will become with the patterns and techniques needed to solve them efficiently.
By consistently reviewing concepts, practicing regularly, and seeking clarification when needed, students can grow more comfortable with mathematical tasks. Eventually, this practice leads to stronger problem-solving skills and the ability to approach new challenges with greater assurance and competence.
Preparing for Algebraic Assessments
Effective preparation for mathematical assessments involves a combination of strategy, practice, and understanding the key concepts. To perform well in any evaluation, it’s important to first become familiar with the material and its various components. Whether it’s equations, expressions, or problem-solving techniques, the goal is to grasp the underlying principles that govern the subject.
Start by reviewing your notes and textbook materials, focusing on areas where you feel less confident. Breaking down complex problems into smaller, more manageable steps can make the process less overwhelming. Additionally, working through practice problems will help reinforce your understanding and expose any gaps in your knowledge that need further attention.
Another effective method is to take timed practice tests, simulating the conditions of the actual assessment. This not only helps with time management but also builds the mental stamina needed to perform well under pressure. By consistently applying these strategies, you’ll build confidence and be well-prepared for any test or exam that comes your way.