Cumulative Exam Algebra 2 Edgenuity Answers Guide

Preparing for a comprehensive assessment in higher-level mathematics requires a solid understanding of various mathematical concepts. The ability to solve complex problems efficiently is crucial, especially when working through an extensive review of the material. Developing a strong foundation in essential mathematical principles will enhance your problem-solving skills and boost your confidence.

Focusing on problem-solving techniques is an effective way to tackle challenging questions. Whether it’s tackling equations, graphing functions, or working through word problems, mastering these skills is vital for success. A methodical approach to learning, along with strategic practice, will lead to better results and a deeper understanding of the subject matter.

Consistency and preparation play a significant role in achieving success. By reviewing key topics, identifying common problem types, and focusing on areas that need improvement, you can make your preparation more efficient and effective. The right resources and study methods will help ensure that you are well-equipped to handle any mathematical challenge that comes your way.

Cumulative Assessment Review for Advanced Math Concepts

Preparing for a comprehensive review of higher-level mathematics can be challenging, but with the right approach, you can tackle even the most difficult problems with confidence. The key to mastering these topics is understanding the underlying principles and practicing problem-solving strategies. This section focuses on how to approach the most common types of questions and provides guidance on how to navigate the assessment process successfully.

Key Areas to Focus On

When reviewing for this type of assessment, it’s important to identify the core topics that will be tested. These often include systems of equations, functions, graphing techniques, and more complex problem types. By understanding the different categories of questions, you can prioritize your study time and focus on areas that require the most attention. Regular practice with sample questions helps reinforce key concepts and boosts overall performance.

Test-Taking Strategies for Success

Effective test-taking strategies are crucial for maximizing your score. Time management, understanding the question types, and knowing how to quickly identify the most efficient solution methods will all play a major role in your success. Additionally, practicing under timed conditions can help improve your ability to think critically and manage time during the actual assessment. By refining these skills, you’ll be better prepared to handle any question that comes your way.

Understanding the Comprehensive Assessment Structure

Grasping the structure of a final review in advanced mathematics is essential for effective preparation. These evaluations typically cover a broad range of topics, requiring students to demonstrate their mastery of concepts learned throughout the course. Knowing what to expect in terms of question types and content distribution can significantly enhance your approach and strategy.

Most assessments are divided into multiple sections, each focusing on a specific mathematical area. These sections may include problem-solving with equations, working with functions, graphing, and applying theoretical knowledge to real-world scenarios. The organization of these sections allows students to showcase their understanding across various topics, testing both practical skills and theoretical knowledge.

Understanding the weight and focus of each section can help you prioritize your study time. By identifying areas that are more heavily represented in the evaluation, you can allocate more attention to them, ensuring you are fully prepared for the types of questions that are most likely to appear.

Key Topics Covered in Advanced Mathematics

In an advanced mathematics course, the material covered is broad and challenging, encompassing a variety of important topics. Understanding these concepts is essential for mastering the subject and performing well in assessments. Below are some of the core areas typically included in such a curriculum:

Functions and Their Graphs – Understanding how to graph various functions, including linear, quadratic, and polynomial functions.
Equations and Inequalities – Solving and analyzing different types of equations, such as systems of equations and inequalities.
Exponential and Logarithmic Functions – Learning about the relationship between exponential growth and decay, and solving logarithmic equations.
Complex Numbers – Working with complex numbers and performing operations such as addition, subtraction, and multiplication.
Sequences and Series – Understanding arithmetic and geometric sequences, as well as how to find the sum of series.
Probability and Statistics – Applying probability rules and understanding statistical concepts like mean, median, and standard deviation.
Mathematical Modeling – Using mathematical functions to model real-world problems and solutions.

Familiarity with these areas will help you approach more complex problems with confidence. By focusing on each topic and practicing various types of questions, you will develop the skills necessary to succeed in more advanced studies and assessments.

How to Prepare for the Assessment Effectively

Preparing for a comprehensive review in mathematics requires a strategic approach to ensure thorough understanding and optimal performance. By organizing your study routine and focusing on key concepts, you can enhance both your knowledge and confidence. Effective preparation involves not just reviewing material, but also practicing under conditions similar to the actual assessment.

Start by identifying the main topics that are likely to appear. This helps prioritize study time and allows you to tackle the most critical areas first. Use practice questions and sample problems to reinforce your skills and improve problem-solving techniques. Simulating test conditions can help you manage time efficiently and reduce anxiety during the actual assessment.

Additionally, reviewing past mistakes and understanding why certain solutions work is an important part of the learning process. This helps identify common patterns and error-prone areas, allowing you to focus on improving weaknesses before the test.

Common Mistakes to Avoid in Advanced Mathematics

When studying advanced mathematical concepts, it’s easy to make certain errors that can affect your understanding and performance. Recognizing and avoiding these mistakes is crucial for mastering the material. Many of these errors stem from misinterpreting questions, skipping steps, or rushing through calculations. By being aware of these common pitfalls, you can significantly improve your problem-solving accuracy.

One frequent mistake is not fully understanding the problem before attempting to solve it. Often, students jump straight into calculations without analyzing what is being asked. This can lead to missing important details and misunderstanding the solution process.

Another common error is neglecting to check work after completing a problem. This can lead to simple calculation mistakes going unnoticed. Taking the time to review each step ensures that no minor errors compromise the final result.

Lastly, not practicing enough with varied problem types can result in a lack of preparedness for more complex questions. Regularly practicing a wide range of problems helps strengthen your skills and builds confidence in tackling unfamiliar challenges.

Platform Features for Advanced Mathematics Learning

The online learning platform designed for advanced mathematics provides a range of features to help students better understand complex concepts and enhance their problem-solving abilities. These tools and resources are specifically built to support learners through interactive lessons, targeted practice, and immediate feedback. By utilizing these features, students can gain a deeper understanding of the material and improve their academic performance.

Interactive Lessons and Tutorials

The platform offers a variety of interactive lessons that break down complicated topics into manageable sections. These lessons are designed to engage students and encourage active learning. Key features include:

Step-by-step tutorials – Detailed instructions to guide students through challenging problems.
Visual aids – Graphs and diagrams that illustrate mathematical concepts in a clear and understandable way.
Practice exercises – Opportunities for learners to apply what they’ve learned in real-world scenarios.

Targeted Practice and Immediate Feedback

The platform also offers personalized practice exercises that allow students to focus on specific areas of difficulty. These exercises are designed to reinforce key skills and improve accuracy. Key benefits include:

Tailored questions – Problems selected based on the student’s performance and progress.
Instant feedback – Detailed explanations of correct and incorrect answers, helping students learn from their mistakes.
Progress tracking – Visual indicators that track progress over time and highlight areas for improvement.

Utilizing Practice Tests for Success

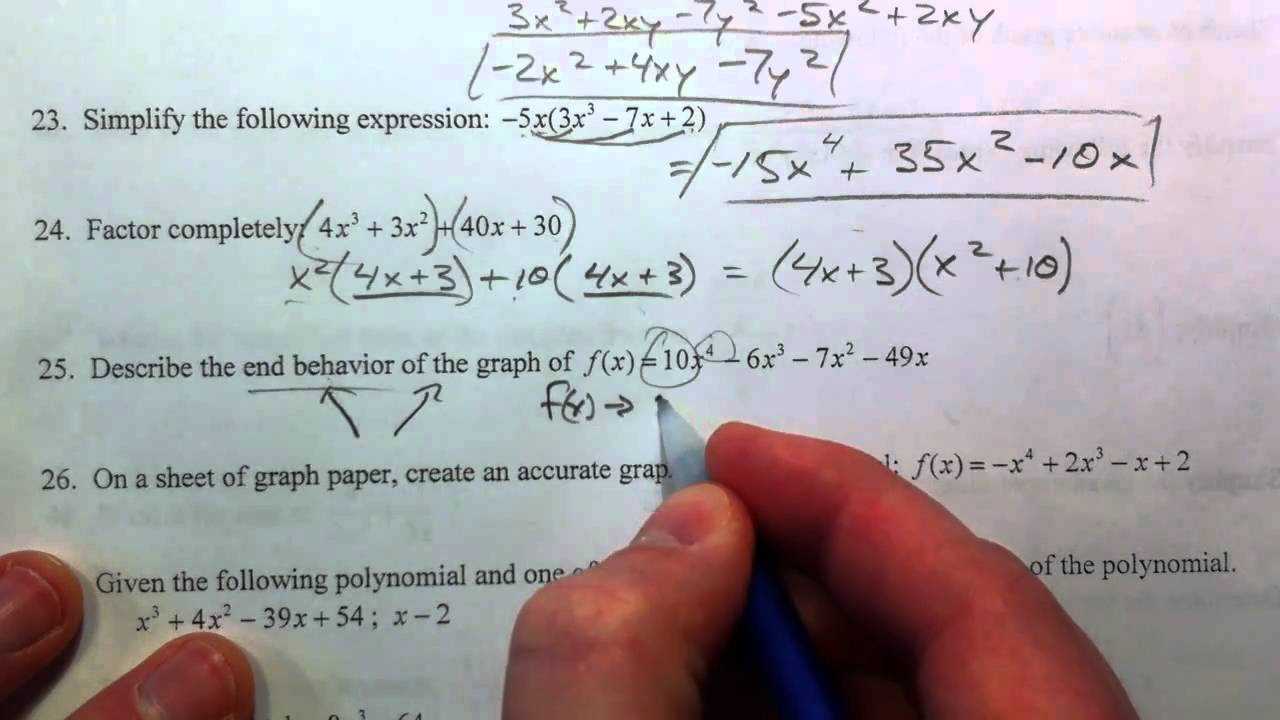
Practice tests are an essential tool in preparing for any major review, offering a valuable opportunity to simulate real assessment conditions. These tests allow students to gauge their understanding of the material, identify areas that need improvement, and refine their test-taking strategies. By regularly using practice tests, learners can build confidence and enhance their performance on the final evaluation.

One of the main benefits of practice tests is the ability to familiarize yourself with the types of questions that are likely to appear. This helps reduce anxiety and increases comfort with the format. Additionally, practicing under timed conditions helps improve time management skills, ensuring that students can allocate their time efficiently during the actual assessment.

Moreover, reviewing the results of practice tests is just as important as taking them. Analyzing incorrect answers and understanding why mistakes were made allows students to strengthen their weaknesses and fine-tune their problem-solving techniques. With consistent practice and thoughtful review, students can maximize their chances of success.

Mastering Quadratic Equations in Advanced Mathematics

Quadratic equations are a fundamental part of higher-level mathematics and mastering them is essential for success in many areas of study. These equations can be solved using a variety of methods, each with its own advantages depending on the specific problem. Understanding the key techniques will allow you to tackle even the most complex problems with confidence.

The most common methods for solving quadratic equations include:

Factoring – This method is effective when the equation can be factored easily into two binomials.
Using the quadratic formula – A universal approach for solving any quadratic equation, especially when factoring is not possible.
Completing the square – A technique used to transform a quadratic equation into a perfect square trinomial, making it easier to solve.

Mastering these methods involves both understanding the theory behind each technique and practicing a variety of problems. By working through different types of quadratic equations, you’ll become more efficient and better prepared to solve these equations under test conditions.

How to Solve Systems of Equations

Solving systems of equations involves finding the values of variables that satisfy two or more equations simultaneously. This process is crucial in many real-world applications, from economics to engineering. Understanding different methods to solve these systems can help you approach problems more effectively and find solutions with ease.

There are several key methods to solve systems of equations:

Substitution method – In this approach, you solve one equation for one variable and then substitute that expression into the other equation to find the solution.
Elimination method – Here, you add or subtract the equations to eliminate one of the variables, making it easier to solve for the remaining variable.
Graphical method – This method involves plotting both equations on a graph to find the point of intersection, which represents the solution.

Each method has its strengths and is best suited for different types of problems. Practicing these techniques will not only help you solve systems efficiently but also give you a deeper understanding of how equations interact and how solutions are derived.

Understanding Polynomials and Their Applications

Polynomials are expressions consisting of variables raised to various powers, combined with coefficients. They are fundamental in mathematics due to their wide range of applications in both theoretical and practical problems. Understanding the structure of polynomials and how to manipulate them is key to solving many types of equations and modeling real-world situations.

In mathematics, polynomials are used to model a variety of phenomena, from physics to economics. They provide valuable insights into the behavior of systems, allowing us to predict outcomes and analyze trends. Below is a table summarizing the different types of polynomials based on the number of terms and their degrees:

Type of Polynomial	Degree	Number of Terms
Monomial	1	1 term
Binomial	2	2 terms
Trinomial	3	3 terms
Quartic	4	4 terms
Quintic	5	5 terms

Mastering polynomials involves understanding their components and learning how to perform operations such as addition, subtraction, multiplication, and factoring. Once you have a solid grasp of polynomial functions, you can apply them to solve problems in areas such as physics (e.g., projectile motion), engineering (e.g., structural analysis), and economics (e.g., profit maximization).

Tips for Graphing Functions Accurately

Graphing functions is an essential skill in mathematics, as it helps visualize relationships between variables and understand how they change. Accurately plotting functions requires attention to detail and a good understanding of the function’s characteristics. By following a few simple strategies, you can ensure your graphs are precise and easy to interpret.

1. Identify Key Points and Intercepts

Before plotting the graph, identify important points such as the x-intercepts, y-intercepts, and any critical points like maxima, minima, or points of inflection. These points give you a solid starting place for your graph and can help you sketch the curve more accurately.

2. Use a Systematic Approach

Start by plotting the function on a grid, marking key points with their corresponding coordinates. Use a consistent scale along both axes, making sure the intervals between points are equal. This will help you avoid distorting the graph and ensure that the overall shape of the function is represented correctly.

Additional Tips for Accurate Graphing:

Label all axes clearly with appropriate scales to avoid confusion.
Use a ruler or straightedge to draw straight lines for linear functions.
For more complex functions, sketch the overall shape of the graph first and then refine it by adding more points.

By practicing these techniques regularly, you will improve your ability to graph functions quickly and accurately, helping you to better understand the relationships represented by those functions.

Exponential and Logarithmic Functions Explained

Exponential and logarithmic functions are closely related and play a crucial role in various fields, from mathematics to science and finance. Understanding these functions involves recognizing how they represent growth, decay, and the relationship between numbers in different scales. While exponential functions model processes that grow or decay at a constant rate, logarithmic functions are their inverse, used to reverse the effects of exponential growth.

Exponential functions are characterized by a constant base raised to a variable exponent. These functions model scenarios like population growth, radioactive decay, and compound interest, where quantities increase or decrease at a fixed percentage rate over time. In contrast, logarithmic functions provide a way to solve for the exponent when the base and the result are known, making them valuable for solving equations that involve exponential terms.

Key Differences:

Exponential functions are of the form y = a * b^x, where b is the base and x is the exponent.
Logarithmic functions are of the form y = log_b(x), where b is the base and x is the result.

Both functions are essential for solving real-world problems that involve growth or decay, making them fundamental in both theoretical mathematics and applied fields like economics, biology, and engineering.

Solving Word Problems with Algebra 2

Word problems can seem challenging at first, but they are simply mathematical puzzles that require you to translate a real-world situation into an equation. In this process, the key is identifying what information is given, what you are asked to find, and how you can use mathematical operations to solve the problem. By breaking down the problem into smaller, manageable steps, you can solve even the most complex situations.

When approaching word problems, it is important to first understand the scenario and identify the variables involved. Next, create an equation based on the relationships between the quantities described. Once you have the equation, you can apply various mathematical methods to solve for the unknowns, such as substitution, elimination, or graphing.

Steps to Solve Word Problems:

Read the problem carefully and identify what is given and what you need to find.
Assign variables to the unknown quantities.
Write an equation or system of equations that represent the relationships in the problem.
Use appropriate methods to solve the equation(s).
Check your solution to ensure it makes sense within the context of the problem.

Example of a Word Problem:

Problem	Equation	Solution
A company sells 50 widgets per day. The cost to produce each widget is $5, and the selling price per widget is $12. What is the company’s profit for one day?	Profit = (Price per widget * Number of widgets) – (Cost per widget * Number of widgets)	Profit = (12 * 50) – (5 * 50) = $350

By following these steps, you can effectively tackle word problems, translating them into solvable equations and finding the solutions with confidence.

Test-Taking Strategies for Algebra 2 Exams

Approaching a test with the right mindset and strategies can significantly improve your performance. A well-organized approach allows you to manage your time effectively and tackle each problem with confidence. The key to success lies in preparation, understanding the test format, and applying efficient problem-solving techniques during the test.

Effective Strategies to Follow:

Time Management: Begin by reviewing the entire test to get an idea of its length and complexity. Allocate time for each section based on its difficulty and point value. Avoid spending too much time on any one question.
Read Questions Carefully: Ensure you fully understand the problem before attempting a solution. Look for keywords and specific instructions that will guide you in forming the right approach.
Start with Familiar Questions: If the test includes a variety of questions, start with the ones you feel most confident about. This will help build momentum and save time for more challenging problems.
Work Step by Step: Break down complex problems into smaller, manageable steps. This will help you stay organized and avoid mistakes. For example, when solving equations, always check your work after each step.
Stay Calm and Focused: Test anxiety can affect your ability to concentrate and think clearly. Take deep breaths, and if you feel overwhelmed, move on to another question and come back later.

Review Your Work: If time permits, go back and review your answers. Ensure all calculations are correct, and check that you’ve answered every question. Reviewing your work can help you spot errors that may have been overlooked during the initial pass.

By applying these strategies, you can approach your test with greater confidence, ensuring a more organized and effective performance. Preparation combined with smart test-taking techniques is the key to success.

How to Stay Focused During the Test

Maintaining focus throughout a test is crucial for achieving the best results. Distractions and anxiety can disrupt your concentration, so it’s important to have strategies in place to stay on track. By preparing mentally and physically, you can enhance your focus and tackle each question with clarity and confidence.

Strategies to Improve Focus

Prepare in Advance: Start by getting enough rest the night before the test. A good night’s sleep ensures your mind is sharp and ready to process information. Avoid cramming the night before, as it can increase stress and hinder focus.
Stay Calm: If you feel anxious during the test, take a few deep breaths to relax. Staying calm allows you to think more clearly and approach problems with a logical mindset.
Break the Test into Segments: Divide the test into smaller, manageable sections. Tackle one problem at a time instead of feeling overwhelmed by the entire test. This approach helps maintain focus and prevents fatigue.
Minimize Distractions: Try to block out external noise or any other distractions in the testing environment. If you’re allowed, use earplugs or focus on your work without looking around the room.
Stay Positive: Maintain a positive mindset throughout the test. If you come across a difficult question, don’t panic. Stay positive and move on to easier questions before returning to the challenging ones.

Post-Test Focus Maintenance

Once you’ve completed a section, take a brief pause to re-focus. Stretching or a short breath break can refresh your mind. This will help you stay alert for the remainder of the test and improve your performance. Maintaining focus isn’t just about staying engaged during the test, but also about pacing yourself to avoid burnout.

By following these tips and staying mindful of your mental and physical state, you can improve your concentration and boost your confidence during the test.

Using Edgenuity Resources to Improve Scores

To enhance performance and achieve better results in assessments, utilizing the various resources available on online learning platforms can be incredibly beneficial. These platforms offer a wide range of tools designed to reinforce understanding, provide practice opportunities, and improve overall knowledge retention. By making the most of these resources, students can better prepare for their assessments and strengthen areas where they may need improvement.

Key Resources for Success

Interactive Lessons: Take advantage of interactive lessons that guide you through complex concepts step-by-step. These lessons provide visual aids, detailed explanations, and interactive elements that help reinforce learning.
Practice Quizzes: Regularly completing practice quizzes helps solidify your understanding of the material. These quizzes test your knowledge and highlight areas where you may need further study, ensuring targeted preparation.
Progress Tracking: Use the progress tracking features to monitor your performance over time. This tool allows you to see areas of strength and weakness, helping you focus your study efforts where they are most needed.
Virtual Tutors: If you’re struggling with certain topics, virtual tutoring options can provide personalized assistance. Tutors can offer additional explanations, answer questions, and provide further practice to boost comprehension.
Study Guides and Review Materials: Many platforms offer study guides and review resources that summarize key concepts and important formulas. These guides are perfect for quick reviews before assessments, ensuring that you have all the essential information at your fingertips.

Maximizing Platform Features for Optimal Results

To truly benefit from these resources, it’s important to create a study plan that incorporates consistent use of the platform’s tools. Schedule regular study sessions, complete practice activities, and use the tracking features to assess your improvement. By staying engaged and committed to using the available resources, you can significantly boost your chances of success.

Taking full advantage of these online resources not only helps improve knowledge but also builds confidence, preparing you to perform your best during assessments.

Final Review Tips Before the Test

As you approach the final assessment, it’s crucial to have a focused and efficient review strategy. The goal is to ensure that you’re fully prepared and confident in applying your knowledge. A well-organized review can help you identify areas that need improvement and boost your readiness for the challenge ahead.

Effective Review Strategies

Prioritize Key Concepts: Focus on the most important topics and concepts that are likely to be tested. Review past assignments, notes, and any practice materials to identify recurring themes.
Work Through Practice Problems: Actively solve practice problems that cover a variety of topics. This not only reinforces your understanding but also helps you become familiar with the format and types of questions that might appear.
Review Mistakes: Go over any mistakes you made during previous quizzes or practice tests. Understanding where you went wrong and why can help you avoid similar errors in the actual test.
Create a Summary Sheet: Summarize important formulas, rules, and key points in a concise document. This will serve as a quick reference during your final review and help reinforce your memory.
Teach What You’ve Learned: One of the best ways to ensure you truly understand a concept is by explaining it to someone else. Try teaching a friend or family member the material. If you can explain it clearly, you know you’ve mastered it.

Final Preparation Tips

Take Breaks: While it’s important to study hard, don’t overwork yourself. Take regular breaks to give your brain a rest and keep your energy levels high.
Get Plenty of Sleep: Ensure you’re well-rested before the test. A good night’s sleep will improve your concentration and cognitive function, helping you stay alert during the assessment.
Stay Calm and Confident: On the day of the test, remain calm. Trust in your preparation and stay confident in your abilities. A positive mindset can make a significant difference in your performance.

By following these strategies, you’ll ensure a more thorough review and enter the assessment with confidence, ready to tackle each question effectively.