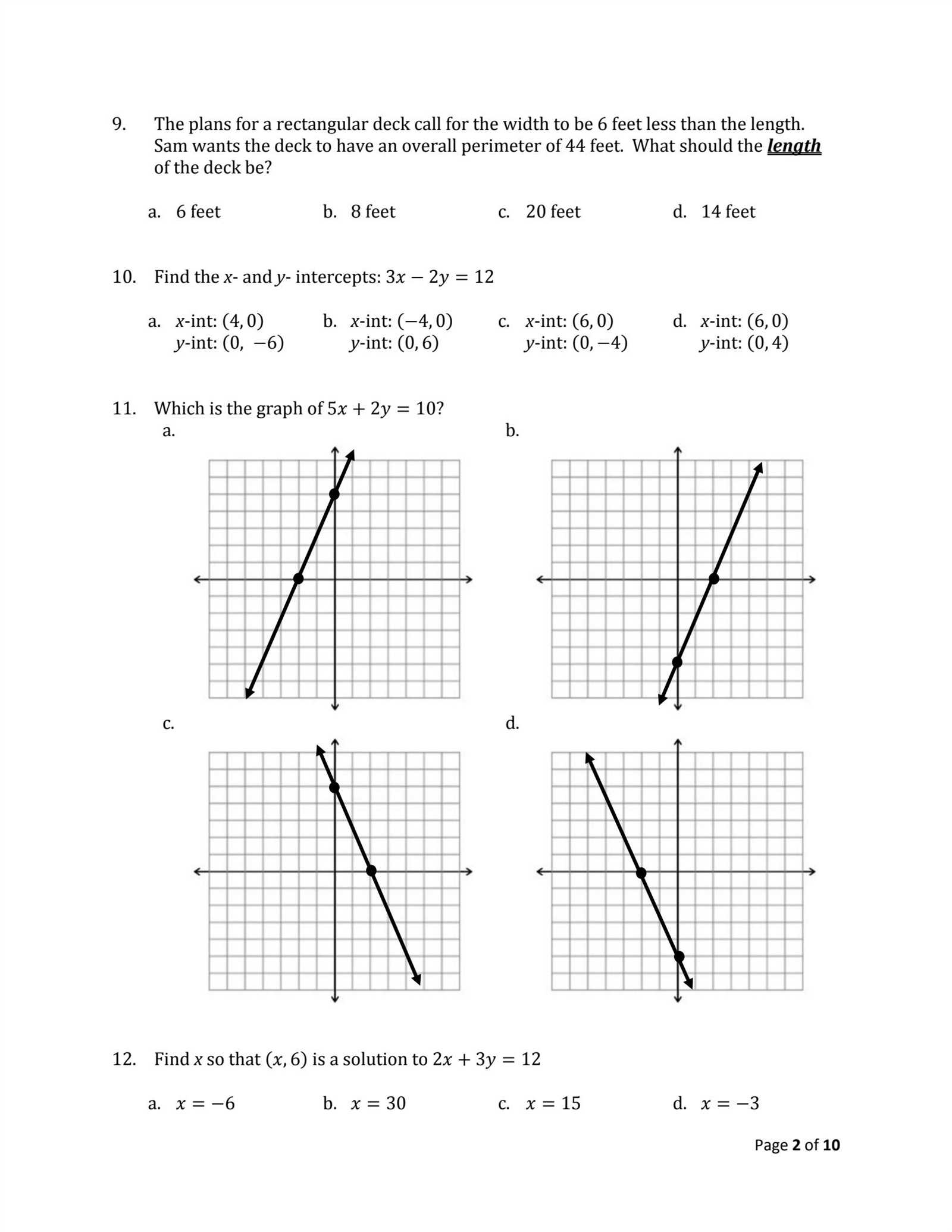
Preparing for a complex math test requires a solid understanding of fundamental principles and techniques. Whether it’s solving equations, interpreting word problems, or applying formulas, each concept builds on the previous one, creating a foundation for success. Having a clear strategy to tackle these challenges can make a significant difference in performance and confidence.
Comprehensive preparation is key. By breaking down problems into manageable steps and practicing regularly, you can approach each question with clarity. It’s important to review essential concepts and focus on areas where improvement is needed. Mastery of key topics will help you solve even the toughest questions efficiently.
Effective study techniques, combined with a strategic approach to problem-solving, can help you succeed in any math assessment. With a focus on understanding rather than memorization, you’ll be ready to face any challenge with confidence.
Mathematical Problem Solving Techniques
Mastering the art of solving complex math problems requires a structured approach. Each challenge can be broken down into smaller, more manageable steps, allowing you to tackle the most difficult questions with ease. A clear understanding of key principles and the ability to apply them effectively can significantly boost your performance.
To approach problems successfully, it’s essential to understand the core concepts, such as:
- Working with equations and variables
- Solving linear and quadratic expressions
- Graphing functions and interpreting data
- Applying geometric principles where necessary
One effective way to prepare for these types of assessments is to practice with a variety of problems. The more familiar you are with different question formats, the more confident you’ll feel during the assessment. Here are some strategies that can help you achieve mastery:
- Practice consistently: Work on problems regularly to strengthen your problem-solving abilities.
- Focus on weaknesses: Identify areas where you struggle and devote more time to them.
- Understand the process: Instead of memorizing formulas, focus on understanding how and why certain methods work.
- Time management: Practice solving problems within a time limit to simulate real testing conditions.
By incorporating these techniques into your study routine, you can improve your problem-solving skills and approach even the most challenging questions with confidence.
Key Concepts to Review for Success
To achieve success in any mathematical assessment, it is crucial to focus on the fundamental concepts that form the foundation of problem-solving. A thorough understanding of these concepts allows you to approach complex questions with confidence and clarity. Reviewing these key topics will prepare you for a wide range of scenarios that may appear on the test.
Here are the essential areas to focus on:
| Concept | Description |
|---|---|
| Equations and Inequalities | Understanding how to manipulate and solve both simple and complex equations is fundamental for solving a wide range of problems. |
| Factoring | Mastering the process of breaking down expressions into their components is vital for simplifying and solving equations. |
| Functions and Graphs | Recognizing the relationships between variables and their graphical representations is a key part of solving problems. |
| Systems of Equations | Being able to solve multiple equations simultaneously is a skill required to tackle more advanced problems. |
| Exponents and Radicals | Understanding the properties of exponents and square roots is necessary for simplifying expressions and solving equations. |
By dedicating time to mastering these concepts, you’ll ensure a solid foundation for solving a variety of mathematical problems with ease. Reviewing and practicing these areas will help you feel well-prepared and ready for any challenge.
Step-by-Step Guide to Problem Solving
Solving complex mathematical problems requires a clear and structured approach. Breaking down a problem into smaller, manageable steps allows for a more organized and effective solution. This step-by-step method ensures that you understand the logic behind each action and minimize the chance of errors.
Here is a guide to follow when approaching any math problem:
| Step | Description |
|---|---|
| 1. Read the problem carefully | Ensure that you fully understand the problem and what is being asked. Identify key information, variables, and required operations. |
| 2. Identify the method | Determine the mathematical approach or formula needed to solve the problem based on the type of question. |
| 3. Set up the equation or expression | Translate the problem into an equation or expression that you can work with, ensuring all components are correctly represented. |
| 4. Solve step-by-step | Follow through with the operations in a logical sequence, making sure to simplify and check each step as you go. |
| 5. Check your solution | After finding the solution, review the steps and substitute your answer back into the original problem to ensure it satisfies the conditions. |
By following this approach, you can efficiently solve even the most complex problems and avoid common mistakes. Consistent practice with this method will help you become more proficient and confident in your mathematical abilities.
Common Mistakes in Math Assessments
When working through mathematical problems, it’s easy to make small errors that can lead to incorrect results. Understanding and avoiding these common mistakes can significantly improve performance and accuracy. Identifying these pitfalls helps you approach problems more carefully and with greater confidence.
Misreading the Problem
One of the most frequent errors occurs when students overlook key details or misunderstand the question entirely. Whether it’s a simple misinterpretation of terms or failing to recognize specific instructions, misreading can lead to incorrect setups or missed opportunities to apply the correct method.
Overlooking Negative Signs

Another common mistake involves mismanagement of negative numbers. Incorrectly adding or subtracting negative signs can drastically change the outcome of an equation. It’s essential to stay vigilant and ensure every negative sign is properly accounted for in each step of the solution.
By being mindful of these and other typical errors, you can avoid unnecessary mistakes and ensure that your problem-solving process is as accurate and efficient as possible. Practicing with a focus on these areas will help you develop more reliable habits and improve your results.
How to Interpret Word Problems
Word problems often present challenges because they require translating real-world scenarios into mathematical expressions. The key to solving these problems is to understand what the question is asking and identify the relevant information. Breaking down the text into manageable parts helps to recognize the variables and relationships involved.
Here is a step-by-step approach to interpreting word problems:
| Step | Description |
|---|---|
| 1. Identify the question | Determine exactly what is being asked. Look for phrases that indicate the required operation, such as “how many,” “what is the total,” or “find the value of.” |
| 2. Extract the given information | Highlight important numbers, variables, and conditions mentioned in the problem. Make sure to identify what each represents (e.g., distances, times, costs). |
| 3. Translate the information | Convert the words into mathematical expressions. Use symbols for quantities and relationships, such as variables for unknowns and arithmetic operations for relationships between them. |
| 4. Set up the equation | Formulate an equation based on the problem’s conditions. This equation will be the foundation for solving the question. |
| 5. Solve the equation | Apply the appropriate mathematical techniques to solve for the unknowns, checking each step as you go to ensure accuracy. |
By following these steps, you can effectively break down any word problem and translate it into a solvable mathematical equation. Understanding the underlying structure of the problem is key to finding the correct solution.
Understanding Equations and Inequalities
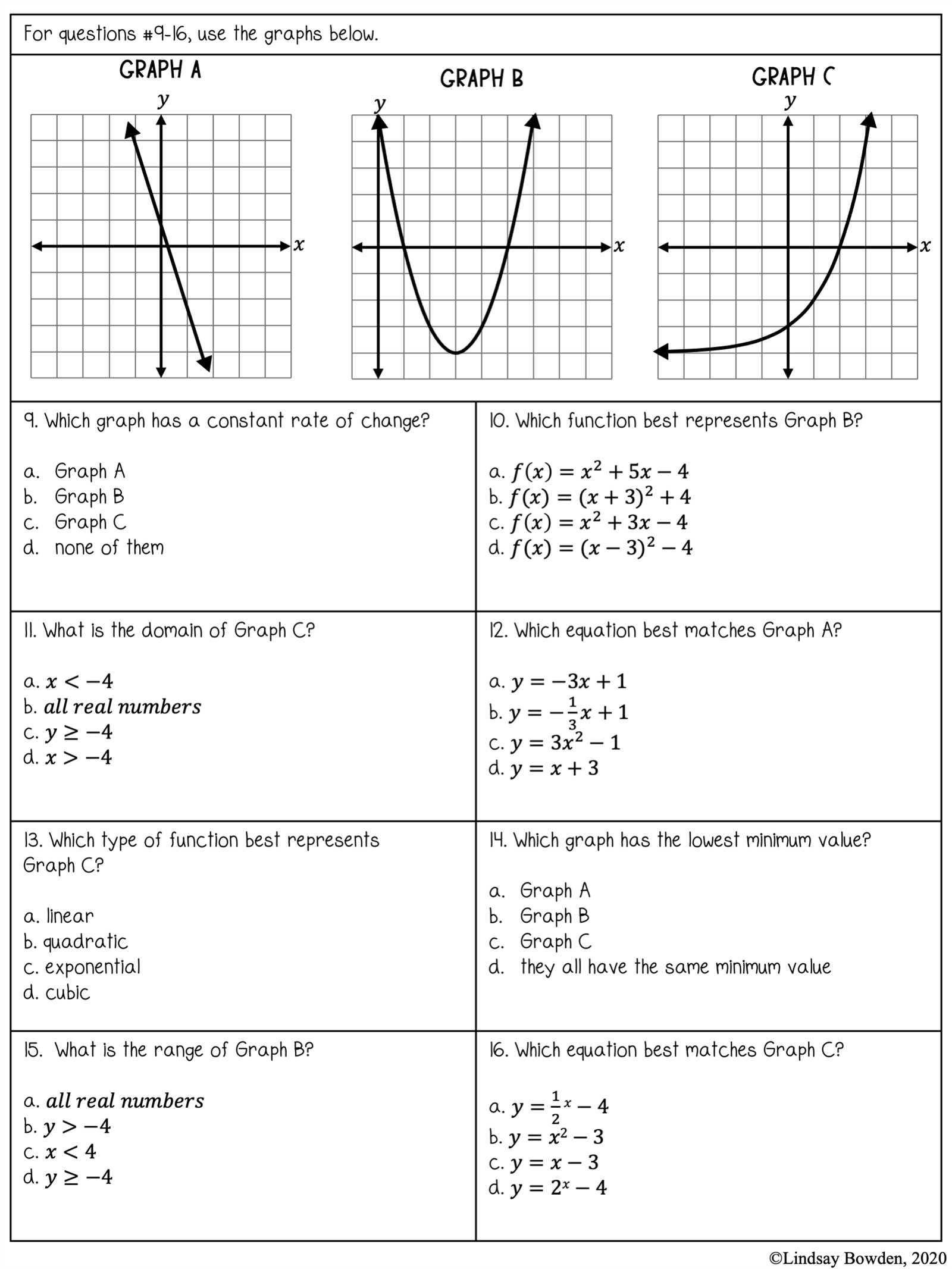
Solving equations and inequalities is essential for solving a variety of mathematical problems. These two concepts allow you to express relationships between quantities and find unknown values. While equations focus on finding exact solutions, inequalities help to describe ranges of values that satisfy certain conditions. Understanding the differences and similarities between them is crucial for solving many types of questions.
Key Differences Between Equations and Inequalities
Equations and inequalities have distinct characteristics. Here’s a brief overview:
- Equations: These are statements that show two expressions are equal. The goal is to find the exact value(s) that satisfy the equation.
- Inequalities: These express relationships where one quantity is greater than or less than another. The solution is a range of values rather than a single value.
Steps for Solving Equations and Inequalities
To solve both types of problems, follow these steps:
- Identify the type: Determine if the problem is an equation or an inequality to apply the correct methods.
- Simplify the expressions: Combine like terms and reduce complex expressions to make solving easier.
- Isolate the variable: Rearrange the equation or inequality to get the variable on one side.
- Check for solutions: For equations, verify the solution by substituting it back into the original. For inequalities, ensure the solution is within the correct range.
By practicing these techniques, you can confidently solve both equations and inequalities and apply them to real-world scenarios effectively.
Strategies for Efficient Time Management
Effective time management is crucial when preparing for any challenging task. Properly allocating your time ensures you can cover all necessary topics without feeling rushed or overwhelmed. By using strategic techniques, you can maximize your productivity and reduce stress, giving you more confidence and control over your study sessions.
Planning Your Study Sessions
To make the most of your study time, create a plan that outlines your goals and priorities. This approach helps you stay focused and ensures you are tackling the most important topics first. Here are some tips:
| Strategy | Description |
|---|---|
| Prioritize Difficult Topics | Begin with the subjects or problems that are most challenging. Tackling them early allows you to devote more time to areas where you need improvement. |
| Use a Timer | Set specific time limits for each study session to avoid distractions and stay focused. A timer can help you stay on track and prevent procrastination. |
| Break Tasks into Smaller Goals | Instead of working on large, overwhelming tasks, break them down into smaller, more manageable steps to maintain motivation and focus. |
| Take Breaks | Allow yourself short breaks between study periods. This will help prevent burnout and keep your mind fresh and engaged. |
Reviewing Progress
Regularly assess your progress to ensure you’re staying on track. Adjust your study plan as needed to focus on areas that need more attention. Consistent reviews can help you identify weaknesses early and provide the opportunity to address them before it’s too late.
By following these time management strategies, you’ll be able to approach your study sessions with greater efficiency, reduce stress, and maximize your chances of success. Effective planning is a key component of staying organized and feeling prepared for any challenge.
Breaking Down Polynomial Problems
When working with polynomials, the problems can sometimes seem complex, but breaking them down into simpler steps can make them much more manageable. Understanding how to handle each part of a polynomial allows you to solve problems more effectively. The process involves recognizing the structure of the equation, simplifying terms, and applying the appropriate methods for addition, subtraction, multiplication, or division.
Steps for Simplifying Polynomial Expressions
Follow these steps to approach polynomial problems methodically:
- Identify like terms: Look for terms with the same degree and combine them. This simplifies the expression and makes it easier to handle.
- Distribute and multiply: When necessary, use the distributive property to multiply terms. This is often seen when multiplying binomials or polynomials.
- Factor when applicable: If the polynomial can be factored, break it down into simpler components. Factoring is often useful for solving equations or simplifying expressions.
- Organize by degree: Ensure that the terms are arranged in descending order by degree, which makes the problem easier to navigate.
Common Techniques for Polynomial Operations
Here are a few methods frequently used to solve polynomial problems:
- Addition and subtraction: Combine like terms by adding or subtracting the coefficients while keeping the variables the same.
- Multiplication: Apply the distributive property or use FOIL (First, Outer, Inner, Last) for binomials to multiply terms effectively.
- Division: For division, use polynomial long division or synthetic division, depending on the situation.
By mastering these fundamental techniques, you’ll be able to tackle polynomial problems with greater confidence and accuracy. Consistent practice is key to becoming proficient in handling various polynomial equations and expressions.
Factoring Techniques to Master
Factoring is an essential skill for solving various types of mathematical problems. It involves breaking down complex expressions into simpler components, which can then be solved or manipulated more easily. By mastering different factoring methods, you can handle a wide range of problems efficiently and gain a deeper understanding of the underlying mathematical principles.
Key Factoring Methods
Here are some of the most common factoring techniques you should master:
- Greatest Common Factor (GCF): Always begin by factoring out the greatest common factor of the terms. This step simplifies the expression and makes further factoring easier.
- Factoring Trinomials: For quadratics in the form ax² + bx + c, look for two numbers that multiply to ac and add to b. This helps split the middle term and factor the expression.
- Difference of Squares: Recognize expressions in the form a² – b², which can be factored into (a – b)(a + b).
- Perfect Square Trinomials: If the expression is a perfect square trinomial, it can be factored into (a + b)² or (a – b)².
Advanced Factoring Techniques

Once you are comfortable with the basics, you can move on to more advanced techniques:
- Grouping: This method is useful for expressions with four terms. Group terms in pairs, factor out the GCF from each pair, and then factor out the common binomial.
- Sum or Difference of Cubes: Recognize expressions like a³ + b³ or a³ – b³, which can be factored into (a + b)(a² – ab + b²) or (a – b)(a² + ab + b²).
- Quadratic Trinomial with Leading Coefficient: When the coefficient of x² is not 1, use the method of splitting the middle term or applying the quadratic formula to find factors.
By practicing these methods regularly, you will develop a strong understanding of factoring and be able to apply it to a variety of problems with confidence and accuracy.
Tips for Solving Quadratic Equations
Solving quadratic equations is a fundamental skill in mathematics. These types of equations, typically in the form ax² + bx + c = 0, can be approached in various ways depending on their structure. By applying the right methods and techniques, you can simplify the process and solve them efficiently. Below are some essential strategies that will help you tackle quadratic equations with confidence.
First, ensure that the equation is written in standard form, ax² + bx + c = 0, where a, b, and c are constants. Once in standard form, choose the method that best fits the equation’s complexity.
Methods for Solving
- Factoring: If the equation can be factored, this is often the simplest method. Look for two numbers that multiply to ac and add to b. Then, split the middle term and factor the expression.
- Quadratic Formula: When factoring is difficult or not possible, use the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a. This formula will work for any quadratic equation, whether it can be factored or not.
- Completing the Square: This method involves manipulating the equation to form a perfect square trinomial. Once completed, take the square root of both sides to find the solutions.
Each of these methods has its own advantages depending on the equation you are working with. While the quadratic formula is versatile and works for all quadratics, factoring and completing the square can sometimes provide quicker solutions when applicable.
Check Your Solutions
After solving the equation, always substitute your solutions back into the original equation to verify their accuracy. This ensures that no errors were made during the solving process.
By mastering these techniques and practicing regularly, you’ll be able to confidently solve any quadratic equation that comes your way.
Graphing Functions on the Exam
Understanding how to graph functions is an essential skill for solving various mathematical problems. Being able to visualize the relationship between variables can provide deeper insights into the behavior of the function. On any assessment, you may be asked to graph different types of functions, ranging from linear to more complex quadratic or exponential equations. Knowing how to approach these problems methodically can help you perform efficiently.
Before graphing, always identify the type of function you’re working with and look for key characteristics that will help you plot the graph accurately. These may include intercepts, asymptotes, or symmetry, which will guide you in sketching the graph step by step.
Key Steps to Follow
- Identify the Function Type: Determine if you’re dealing with a linear, quadratic, cubic, or any other type of function. Each has its own set of rules for graphing.
- Find Key Points: Calculate the x-intercepts, y-intercepts, and any other points of interest like turning points or asymptotes.
- Plot Points on a Grid: Mark the points you have identified on a coordinate plane. Be sure to label the axes clearly for easier visualization.
- Draw the Curve: Based on the function’s properties, connect the points smoothly. Remember, some functions will have straight lines (like linear functions), while others will curve (like quadratic or exponential functions).
Practice for Accuracy
To master graphing, practice is key. The more familiar you become with the specific characteristics of different functions, the more easily you’ll be able to graph them accurately. Always double-check your work by verifying if the graph aligns with the expected behavior of the function.
With consistent practice and understanding of key concepts, graphing will become an intuitive process, allowing you to confidently tackle these types of problems in any assessment.
Working with Rational Expressions

Rational expressions are fractions where both the numerator and denominator are polynomials. These expressions often appear in various mathematical problems and require specific techniques to simplify, multiply, divide, add, or subtract. Mastering how to manipulate these expressions will enhance your problem-solving abilities and help you tackle more complex topics.
The first step when working with rational expressions is to check for any restrictions, such as values that would make the denominator equal to zero, as these would make the expression undefined. Once you’ve identified any restrictions, you can begin simplifying or solving the expression based on the operation at hand.
Simplifying Rational Expressions
To simplify a rational expression, look for common factors in the numerator and denominator. By factoring both parts and canceling out common factors, you can reduce the expression to its simplest form. Here’s a general approach:
- Factor: Factor both the numerator and denominator completely.
- Cancel Common Terms: Cancel out any terms that appear in both the numerator and denominator.
- Check for Restrictions: After simplifying, always ensure that none of the factors in the denominator are zero.
Operations with Rational Expressions

When performing operations like addition, subtraction, multiplication, or division with rational expressions, it’s important to follow a systematic approach:
- Addition/Subtraction: Find a common denominator before combining the numerators. Simplify the resulting expression.
- Multiplication: Multiply the numerators and denominators directly, then simplify by canceling common factors.
- Division: Invert the second rational expression (find the reciprocal) and multiply.
By following these steps, you can efficiently handle operations involving rational expressions and ensure accuracy in your work.
Analyzing Systems of Equations
Systems of equations involve multiple equations with the same set of variables. Solving these systems allows us to find the values that satisfy all the equations simultaneously. Whether you’re dealing with two linear equations or more complex ones, understanding the methods to solve these systems is essential for mastering mathematical problem-solving.
There are several approaches to solving systems, including substitution, elimination, and graphical methods. Each method has its strengths, depending on the type of system you’re working with. By analyzing the system carefully, you can choose the most efficient method and proceed step by step to find the solution.
Substitution Method

The substitution method involves solving one of the equations for one variable and then substituting that expression into the other equation. This reduces the system to a single equation with one variable, which can be solved more easily. Once you have the solution for one variable, substitute it back into one of the original equations to find the value of the second variable.
Elimination Method
The elimination method is based on adding or subtracting the equations to eliminate one of the variables. To use this method effectively, you may need to multiply one or both equations by a constant so that the coefficients of one variable match. Once one variable is eliminated, the system simplifies to a single equation, which can be solved for the remaining variable.
By carefully analyzing the structure of the system, you can apply the best method to find the solution. Whether through substitution, elimination, or another approach, the goal is to find the values that satisfy all the equations in the system.
Mastering Exponents and Logarithms
Exponents and logarithms are essential concepts that often go hand in hand. Mastering these topics allows you to simplify complex expressions and solve equations more effectively. Exponents deal with repeated multiplication, while logarithms provide a way to reverse that operation. Understanding how to manipulate both is crucial for tackling a wide range of mathematical problems.
When working with exponents, it’s important to familiarize yourself with the basic rules, such as the product, quotient, and power rules. These rules help simplify expressions involving powers and make calculations much quicker. Similarly, logarithms are the inverse of exponentiation, and learning how to work with logarithmic functions is vital for solving equations involving exponential growth or decay.
Once you’re comfortable with the properties of exponents and logarithms, applying them to real-world problems, such as population growth or financial calculations, becomes much easier. The key to mastering these topics is regular practice and a deep understanding of how they relate to each other.
Utilizing the Quadratic Formula
The quadratic formula is a powerful tool for solving second-degree equations, which often arise in various real-world scenarios. It provides a straightforward method to find the roots of an equation, especially when factoring is challenging or not possible. This formula can be applied to equations of the form ax² + bx + c = 0, where a, b, and c are constants.
By plugging the values of a, b, and c into the formula, you can easily calculate the solutions. The quadratic formula is expressed as:
x = (-b ± √(b² – 4ac)) / 2a
Understanding the discriminant (b² – 4ac) is key to interpreting the results. If the discriminant is positive, you get two real solutions; if it’s zero, you have one real solution; and if it’s negative, the equation has no real solutions but two complex ones.
When to Use the Quadratic Formula
While there are other methods to solve second-degree equations, the quadratic formula is often the most reliable and applicable, especially when the equation is not easily factorable. It is particularly useful in cases where the coefficients do not lend themselves to simple factoring or when you need to ensure all possible solutions are found.
Example of Solving Using the Quadratic Formula
Consider the equation 2x² – 4x – 6 = 0. To solve for x, first identify a = 2, b = -4, and c = -6. Plugging these values into the quadratic formula:
x = (-(-4) ± √((-4)² – 4(2)(-6))) / 2(2)
After simplifying the terms, you will arrive at the solutions for x. This illustrates how the quadratic formula is an essential tool for solving more complex equations efficiently.
Test Anxiety and How to Overcome It
Feeling nervous or overwhelmed before an important assessment is common, but it can often affect performance. This sense of worry, sometimes referred to as test anxiety, can manifest physically and mentally, making it difficult to concentrate and recall information. It’s essential to recognize the signs and develop strategies to manage stress effectively.
While some level of nervousness can motivate focus and preparation, excessive anxiety can be paralyzing. The key to overcoming it lies in understanding its triggers and learning how to reduce its impact on your mindset and performance. With the right approach, you can improve your ability to stay calm and perform well under pressure.
Recognizing the Symptoms of Test Anxiety
Test anxiety can affect individuals in various ways. Some common symptoms include:
- Increased heart rate and shallow breathing
- Difficulty concentrating or focusing
- Feeling overwhelmed or helpless
- Physical symptoms like headaches or stomachaches
- Negative thoughts about performance or outcomes
It’s important to acknowledge these signs early, so you can address them before they interfere with your success.
Effective Strategies to Manage Stress
There are several strategies you can employ to manage anxiety and perform at your best:
- Practice deep breathing: Slow, deep breaths can help reduce physical tension and calm your mind.
- Visualize success: Imagine yourself confidently completing the task, which can boost your self-assurance.
- Break down study material: Organize your study sessions into smaller, manageable sections to avoid feeling overwhelmed.
- Get enough rest: Adequate sleep is vital for cognitive function and emotional stability.
- Stay positive: Replace negative thoughts with affirmations and remind yourself that you are prepared.
By incorporating these techniques, you can significantly reduce anxiety and improve your overall experience when facing any assessment or challenge.
Practice Exams for Better Preparation
One of the most effective ways to prepare for a significant assessment is by taking practice tests. These exercises mimic the format and timing of the actual challenges, helping you become familiar with the types of questions you may encounter. In addition, they provide a valuable opportunity to identify areas of strength and weakness in your understanding of the material.
By engaging in these practice sessions, you can develop a deeper comprehension of key concepts and refine your problem-solving techniques. The repetition and feedback from these exercises also help build confidence, reduce anxiety, and improve time management skills.
Benefits of Practicing with Mock Tests
Here are several reasons why practice tests are essential for effective preparation:
- Improved Time Management: Simulating timed conditions helps you get accustomed to pacing yourself during the actual assessment.
- Enhanced Focus: Practice exams allow you to concentrate on specific areas, sharpening your focus on what matters most.
- Better Retention: The more you engage with the material, the better you retain the information, making recall easier when it counts.
- Identifying Knowledge Gaps: Practice exams highlight areas that need further review, ensuring you focus your efforts where they are most needed.
Tips for Maximizing the Effectiveness of Practice Sessions
To get the most out of practice tests, follow these strategies:
- Simulate Real Conditions: Take the test in an environment that mimics actual testing conditions, including time constraints and minimal distractions.
- Review Incorrect Answers: After completing each practice session, go over any mistakes and understand why the correct answers are right.
- Track Your Progress: Keep a record of your performance across multiple practice tests to track improvements and adjust your study plan accordingly.
- Vary the Question Types: Practice with a variety of questions to ensure you are well-prepared for every possible challenge.
By consistently practicing and evaluating your performance, you’ll approach the real challenge with greater assurance and clarity, ready to perform at your best.