
Mathematics can be challenging, especially when it comes to assessing your skills. Whether you’re reviewing for a crucial assessment or looking to solidify your understanding, knowing how to approach different types of problems is essential for success. This section will guide you through key strategies, offer practical practice, and provide valuable resources to help you prepare effectively.
Effective preparation begins by recognizing the core concepts you need to focus on. Familiarizing yourself with various problem types and how they’re typically structured can give you the confidence to tackle even the toughest questions. Step-by-step solutions are essential in identifying patterns, correcting mistakes, and refining your technique.
Additionally, practicing regularly and reviewing common pitfalls will sharpen your problem-solving ability. By focusing on essential skills and using the right techniques, you can approach each question methodically and boost your chances of performing well.
Pre Mathematics Assessment and Solutions
Achieving success in mathematics assessments requires a combination of understanding key concepts and knowing how to apply them effectively. This section provides a comprehensive look at common question types, problem-solving strategies, and detailed solutions to help you prepare thoroughly and confidently for your upcoming test.
Key Concepts to Focus On
Understanding the essential principles is critical when approaching any assessment. Focus on mastering the fundamental rules, such as working with equations, manipulating expressions, and solving simple and complex problems. These concepts form the backbone of any challenge you may face and will guide you through even the most difficult questions.
Step-by-Step Problem Solving
Breaking down problems into smaller, manageable steps is key to ensuring accuracy. By applying methodical strategies and double-checking each solution, you reduce the likelihood of making simple errors. Practice using this approach regularly, and over time, you’ll improve both your speed and confidence.
Remember, regular practice is vital. Reviewing solved examples and repeating similar problems will reinforce your knowledge and help solidify your skills for the assessment ahead.
Essential Concepts to Review
Before taking any important mathematics assessment, it’s crucial to revisit the fundamental principles that are often tested. By focusing on these key ideas, you can build a strong foundation for tackling a variety of questions efficiently. Understanding how to apply these concepts will significantly improve your ability to perform well under pressure.
Key areas to focus on include solving linear equations, working with basic arithmetic operations, and understanding how to manipulate fractions and decimals. These core topics are often integrated into more complex problems, so a solid grasp of them is essential for success.
Additionally, mastering word problems and learning how to interpret and translate them into mathematical expressions is a vital skill. Practicing different types of problems will ensure you’re prepared for any question that comes your way.
Common Mistakes to Avoid
When preparing for a mathematics assessment, recognizing and avoiding common errors can significantly improve your performance. Small mistakes, such as misreading a question or skipping steps, can lead to incorrect results even when the overall understanding is solid. Being aware of these pitfalls and taking steps to prevent them can make a big difference.
One frequent mistake is not fully simplifying expressions before proceeding with further calculations. Skipping this step can result in more complicated errors later in the process. Another common issue is rushing through word problems, leading to incorrect interpretations of the information. It’s crucial to carefully read and translate each part of the problem into a mathematical format before solving.
Finally, failing to double-check work is another area where many students lose points. Even when the process seems straightforward, re-evaluating the solutions can help catch simple arithmetic mistakes or overlooked steps.
Step-by-Step Solution Guide
Breaking down problems into clear, manageable steps is a proven method for ensuring accuracy and success. By following a structured approach, you can tackle complex questions one at a time, ensuring that each part is understood and solved correctly. Below is an example of how to solve a typical problem using a step-by-step method.
| Step | Action | Explanation |
|---|---|---|
| 1 | Read the problem carefully | Understand the question and identify key information. |
| 2 | Identify the operation | Determine whether the problem requires addition, subtraction, multiplication, or division. |
| 3 | Set up the equation | Translate the word problem into a mathematical expression or equation. |
| 4 | Solve the equation | Apply the appropriate operations in the correct order to simplify the equation. |
| 5 | Check the solution | Verify the solution by plugging it back into the original equation. |
This systematic approach helps prevent mistakes and ensures that no important steps are overlooked. Practicing this method will make it easier to solve problems effectively during the assessment.
Key Formulas to Remember
Mastering the fundamental formulas used in solving mathematical problems is crucial for success in any assessment. These formulas act as tools that help simplify complex questions, providing clear solutions when applied correctly. Below is a list of essential formulas that will help guide you through a variety of problems.
- Equation of a line: y = mx + b
- Area of a rectangle: A = length × width
- Perimeter of a rectangle: P = 2(length + width)
- Area of a triangle: A = ½ × base × height
- Volume of a rectangular prism: V = length × width × height
- Simple interest: I = P × r × t
It is also important to understand how to manipulate these formulas. For example, rearranging an equation to solve for a specific variable is a key skill. Practicing these formulas and ensuring you can apply them quickly will improve both your speed and accuracy.
- Rearranging equations: Solve for a specific variable in terms of others.
- Using the distributive property: a(b + c) = ab + ac
- Factoring: Recognize common factors to simplify expressions.
By reviewing and regularly practicing these key formulas, you’ll be well-prepared to handle a wide range of problems effectively.
Understanding Basic Equations
Grasping the fundamentals of simple mathematical relationships is essential for solving problems efficiently. These basic equations serve as the foundation for more complex challenges, and understanding how to manipulate them can significantly improve your problem-solving skills. Below are some key principles to remember when working with equations.
- Equality: An equation represents a balance between two expressions, with both sides being equal.
- Variables: Letters such as x, y, or z are used to represent unknown values in equations.
- Operations: Equations often involve addition, subtraction, multiplication, or division.
- Solving: The goal is to isolate the variable and determine its value by performing inverse operations.
For example, consider the equation 2x + 3 = 7. To solve for x, follow these steps:
- Subtract 3 from both sides: 2x = 4
- Divide both sides by 2: x = 2
Practicing these types of equations will strengthen your understanding and improve your ability to solve similar problems efficiently. Remember, the key is to simplify the equation step by step until the variable is isolated and its value is clear.
Practice Questions for Mastery
To truly master any mathematical concept, regular practice is essential. Solving a variety of problems helps solidify your understanding and boosts your confidence. Below are several practice questions that cover key concepts, providing opportunities to apply what you’ve learned and enhance your skills.
- Solve for x: 3x – 5 = 10
- Simplify: 4(2x + 3) – 5x
- Find the area: A rectangle has a length of 8 units and a width of 5 units.
- Calculate the perimeter: A triangle has sides of 5, 7, and 10 units.
- Factor: x² + 5x + 6
Working through these types of problems regularly will reinforce key skills such as equation solving, simplification, and geometry. Each question is designed to strengthen your ability to approach different problem types, making you more proficient as you continue practicing.
Tip: After attempting each problem, review your steps carefully to identify any mistakes or areas for improvement. This process will help you become more accurate and faster over time.
Tips for Efficient Study Sessions
Maximizing the effectiveness of your study time is key to improving both understanding and retention of mathematical concepts. A focused approach, along with strategic planning, will help you make the most of each session. Here are some tips to guide your study routine.
| Tip | Description |
|---|---|
| Set specific goals | Focus on one concept or problem type at a time to avoid feeling overwhelmed. |
| Break study time into chunks | Study in intervals, such as 25-minute sessions with 5-minute breaks to maintain concentration. |
| Practice actively | Engage with problems and solutions rather than passively reading or watching tutorials. |
| Review regularly | Revisit past material frequently to reinforce long-term memory. |
| Use a variety of resources | Try different study aids like books, online tutorials, and practice worksheets to deepen understanding. |
By incorporating these strategies into your routine, you will develop better study habits and increase your efficiency. Consistency and focus are key components of any successful study plan.
Time Management During the Exam
Effective time management is crucial when faced with a set of problems under a time constraint. Allocating the right amount of time to each section and maintaining a steady pace can prevent unnecessary stress and improve your performance. Below are some strategies to help you manage your time efficiently during the assessment.
Prioritize Questions

- Start with easier questions: Answer the simpler problems first to build confidence and secure quick points.
- Identify time-consuming questions: If a question seems challenging, move on and return to it later if time permits.
- Set a time limit per question: Allocate a specific amount of time for each question and stick to it.
Track Your Progress

- Keep an eye on the clock: Regularly check the time to ensure you’re on track to complete all sections.
- Adjust your pace as needed: If you’re spending too much time on one question, adjust your speed for the remaining ones.
- Leave some time to review: Always allocate a few minutes at the end to go back and double-check your answers.
By practicing these techniques, you can maintain a steady pace and ensure that you complete all parts of the assessment effectively, without feeling rushed.
How to Tackle Word Problems
Word problems can seem intimidating at first, but breaking them down into manageable steps makes them much easier to solve. The key is to understand what the problem is asking, identify the relevant information, and apply the appropriate mathematical operations. Here’s a guide to help you approach word problems effectively.
Steps to Solve Word Problems
- Read carefully: Read the problem at least twice to fully understand what is being asked.
- Identify key information: Look for numbers, units, and relationships that are essential to solving the problem.
- Write an equation: Translate the word problem into a mathematical equation or expression.
- Solve the equation: Apply the necessary operations to find the solution.
- Check your work: Verify that your solution makes sense in the context of the problem.
Common Strategies for Word Problems

- Draw a diagram: Visualizing the problem can help clarify the relationships between different elements.
- Use estimation: Estimate the solution before solving to help guide your approach and check the reasonableness of your answer.
- Break the problem into smaller parts: If the problem has multiple steps, tackle each part individually before combining the results.
By following these strategies, you can improve your ability to solve word problems confidently and efficiently. Practice will help you recognize common patterns, making the process smoother over time.
Preparing for Multiple Choice Questions
Multiple choice questions often require a different approach compared to open-ended problems. Success in these questions depends on your ability to quickly analyze each option and apply your knowledge effectively. Here are some strategies to help you prepare for and tackle these types of questions.
Effective Strategies for Multiple Choice
- Read the question carefully: Make sure you understand what the question is asking before considering the options.
- Eliminate obviously incorrect options: Narrow down the choices by removing answers that are clearly wrong.
- Look for clues in the question: Sometimes, the wording of the question can help you identify the correct answer or rule out certain choices.
- Use your knowledge of concepts: Apply what you know about key principles to evaluate the options logically.
- Don’t rush: Take your time to think through each question. It’s better to make an informed choice than to guess quickly.
How to Handle Uncertainty
- Make an educated guess: If you’re unsure, try to choose the answer that seems most aligned with what you’ve studied.
- Return to tough questions: If time allows, mark difficult questions to revisit after completing the rest of the test.
- Watch for trick options: Multiple choice questions often include options designed to mislead, so stay alert for any subtle clues.
By following these methods, you can increase your chances of answering multiple choice questions accurately and confidently. Preparation and strategic thinking are key to mastering these questions effectively.
Using Graphs and Charts Effectively
Graphs and charts are powerful tools for visually representing data, making it easier to interpret and analyze. When used correctly, they can simplify complex information and provide clarity in problem-solving. Here’s how you can use these visual aids to enhance your understanding and approach to problems.
How to Interpret Graphs and Charts
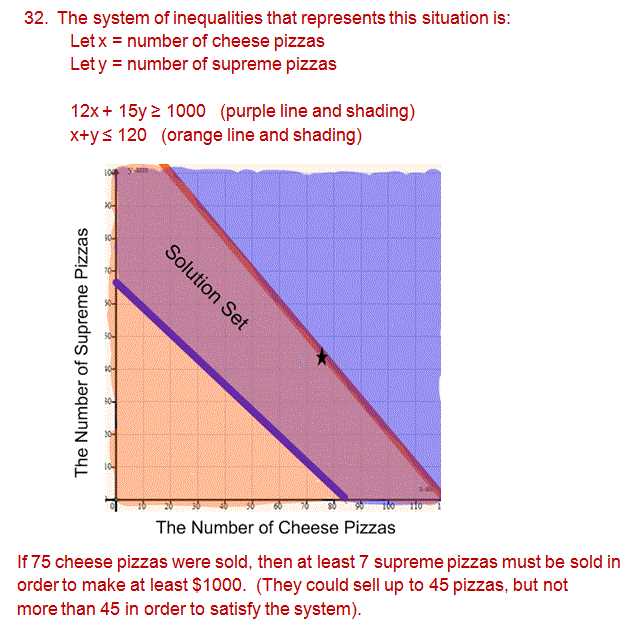
- Understand the axes: Identify what each axis represents, including the scale and units of measurement.
- Focus on trends: Look for patterns such as increases, decreases, or stability in the data. These trends can help you answer questions more effectively.
- Identify key points: Pay attention to important data points on the graph, such as the highest, lowest, or average values.
- Check labels and legends: Always verify the labels to ensure you are interpreting the information correctly.
Strategies for Using Graphs and Charts in Problem Solving

- Translate visual data into equations: Use graphs to identify relationships between variables, which can then be translated into equations for further analysis.
- Use graphs to verify answers: If you’ve calculated an answer, check if it matches the visual representation on the graph.
- Practice interpreting different types of charts: Familiarize yourself with bar graphs, line graphs, and pie charts to quickly adapt to various problem types.
By mastering the use of graphs and charts, you can improve your ability to solve problems accurately and efficiently. These visual tools allow you to make sense of data at a glance, saving time and increasing confidence during assessments.
Important Algebraic Properties to Know
Understanding key properties is essential when working with mathematical expressions and equations. These foundational principles help you simplify and manipulate expressions, making complex problems more manageable. Here are some of the most important concepts to grasp for solving problems efficiently.
Key Properties of Operations
- Commutative Property: The order of numbers does not affect the result when adding or multiplying. For example, a + b = b + a and a * b = b * a.
- Associative Property: The way numbers are grouped in addition or multiplication does not change the result. For example, (a + b) + c = a + (b + c) and (a * b) * c = a * (b * c).
- Distributive Property: Multiplying a number by a sum or difference is the same as multiplying the number by each term separately. For example, a * (b + c) = a * b + a * c.
Identifying Important Properties in Equations
Applying these properties effectively can greatly simplify solving equations. Below is a summary of some additional useful algebraic properties:
| Property | Example |
|---|---|
| Identity Property | a + 0 = a, a * 1 = a |
| Inverse Property | a + (-a) = 0, a * (1/a) = 1 |
| Zero Property of Multiplication | a * 0 = 0 |
By mastering these properties, you can approach mathematical problems with more confidence and efficiency. Understanding how these principles work together allows for faster problem-solving and a deeper understanding of math fundamentals.
Identifying and Solving Inequalities
Understanding how to work with inequalities is an essential skill in mathematics. Inequalities represent relationships where one value is either less than, greater than, or unequal to another. These expressions are similar to equations, but they involve a range of possible solutions rather than a single value. The key to solving inequalities is applying proper techniques while keeping the inequality sign consistent throughout the problem.
Types of Inequalities
- Less Than ( Indicates that one value is smaller than another. Example: x < 5.
- Greater Than (>): Indicates that one value is larger than another. Example: x > 3.
- Less Than or Equal To (≤): Indicates that one value is smaller or equal to another. Example: x ≤ 7.
- Greater Than or Equal To (≥): Indicates that one value is larger or equal to another. Example: x ≥ 2.
- Not Equal To (≠): Indicates that two values are not equal. Example: x ≠ 4.
Steps for Solving Inequalities
- Isolate the variable: Just like equations, start by moving terms to isolate the variable on one side of the inequality.
- Perform the same operation: Apply the same operations (addition, subtraction, multiplication, or division) to both sides of the inequality.
- Flip the sign when multiplying or dividing by a negative number: This is a critical step when solving inequalities–if you multiply or divide both sides of an inequality by a negative number, you must flip the inequality sign. Example: -2x > 6 becomes x < -3.
- Graph the solution: After solving, represent the solution on a number line or using interval notation to clearly show the possible values of the variable.
By mastering these methods, you can effectively identify and solve inequalities, making it easier to work with a variety of mathematical scenarios that involve constraints or limits. Whether dealing with real-world applications or abstract problems, understanding inequalities is crucial for solving many types of problems in mathematics.
Reviewing Key Mathematical Terms
Having a solid understanding of mathematical terminology is essential for solving problems efficiently. Recognizing and knowing how to apply different terms can make a significant difference in how quickly and accurately you approach a problem. Whether you’re working with numbers, equations, or functions, understanding the core vocabulary is a step toward mastery.
Basic Mathematical Concepts
- Variable: A symbol, usually a letter, that represents an unknown value in an equation or expression. Example: x in x + 5 = 10.
- Constant: A fixed value that does not change. Example: In the expression 3x + 4, 4 is a constant.
- Expression: A combination of numbers, variables, and operations that does not have an equality sign. Example: 2x + 3.
- Equation: A mathematical sentence that shows two expressions are equal. Example: 2x + 3 = 7.
Operations and Relations
- Addition: The process of finding the total of two or more numbers. Example: 3 + 4 = 7.
- Subtraction: The operation of taking one number away from another. Example: 5 – 2 = 3.
- Multiplication: The operation of repeated addition. Example: 4 × 3 = 12.
- Division: The process of splitting a number into equal parts. Example: 12 ÷ 4 = 3.
By regularly reviewing these essential terms and their applications, you’ll build a strong foundation that will serve you in tackling more complex topics. A clear understanding of mathematical language enables more efficient problem-solving and supports better comprehension when dealing with new concepts.
How to Check Your Results

Verifying your solutions is a crucial step in ensuring accuracy and understanding your approach. It not only helps catch simple mistakes but also reinforces the concepts behind each problem. Whether you’re solving for an unknown value, simplifying expressions, or working with functions, reviewing your work thoroughly will lead to better outcomes.
Start by retracing your steps. Carefully go through each calculation or operation to confirm that you followed the correct method. If possible, substitute your solution back into the original problem to see if it holds true. For example, if you’re solving an equation, substitute your value for the variable and check if both sides are equal.
Another effective strategy is to use a different method to solve the same problem. If you arrive at the same result using multiple approaches, it’s a strong indication that your solution is correct. In some cases, graphing or using estimation techniques can provide additional verification.
Lastly, ensure that your solution makes sense in the context of the problem. Check for any inconsistencies or unrealistic answers that may have resulted from misinterpretation or errors in your calculations. A careful review not only improves accuracy but also enhances your problem-solving skills for future challenges.
Stress Management Tips for Important Assessments

Preparing for significant evaluations can be overwhelming, and the pressure to perform well often leads to stress. Effective stress management is essential not only for your mental well-being but also to enhance focus and performance. Developing healthy habits, staying organized, and practicing relaxation techniques can help reduce anxiety and allow you to approach your tasks with clarity.
Healthy Study Habits
Building a balanced study routine is one of the most important steps to managing stress. Avoid last-minute cramming, as it increases anxiety and reduces retention. Instead, break down your study material into manageable sections, and allocate specific time blocks for each topic. Ensure that you take regular breaks to rest your mind and prevent burnout.
Relaxation Techniques
Incorporating relaxation practices into your study regimen can significantly help alleviate stress. Simple techniques such as deep breathing, meditation, or mindfulness can calm your nerves and help you regain focus. Physical activities, like stretching or light exercise, also improve circulation and relieve tension, making it easier to concentrate.
Nutrition and Sleep
Maintaining a balanced diet and ensuring you get enough rest is essential for managing stress effectively. Avoid high amounts of caffeine or sugar, as they can disrupt your energy levels and mood. A well-rested mind is better equipped to retain information and solve problems. Aim for 7-8 hours of sleep each night to keep your mind sharp and your stress levels low.
Time Management
Effective time management allows you to prioritize tasks and avoid the overwhelming feeling of having too much to do. Create a realistic study schedule and stick to it. Break large tasks into smaller, more achievable steps and tackle them one at a time. Staying organized and on track will reduce unnecessary stress and help you feel more in control of your preparation.
Positive Mindset
Approach the situation with a positive mindset. Remind yourself that this is an opportunity to showcase your abilities, not a source of fear. Avoid negative self-talk and focus on the progress you’ve made. Confidence is key to managing stress and performing at your best.
| Tip | Benefit |
|---|---|
| Healthy Study Habits | Reduces anxiety, enhances focus |
| Relaxation Techniques | Calms nerves, improves concentration |
| Nutrition and Sleep | Boosts energy, promotes mental clarity |
| Time Management | Increases efficiency, reduces overwhelm |
| Positive Mindset | Builds confidence, reduces negative stress |
Where to Find Additional Practice Resources
Enhancing your understanding and skills requires consistent practice, and there are many resources available to help you reinforce concepts. Whether you’re looking for free online tools, textbooks, or interactive exercises, there are numerous ways to supplement your learning and gain more experience. These resources can provide diverse problems, detailed explanations, and step-by-step solutions to help you master the material.
Online Platforms and Websites
There are numerous educational websites offering free practice exercises, tutorials, and quizzes. Many platforms provide personalized learning paths to target specific areas where you may need improvement. Websites like Khan Academy, IXL, and Mathway offer interactive lessons and practice problems at varying levels of difficulty. These platforms also track your progress, helping you stay motivated.
Workbooks and Study Guides
Traditional study guides and workbooks are valuable tools for reinforcing key concepts. They typically provide a range of practice questions, including easy, moderate, and challenging problems. Popular publishers like Pearson and McGraw-Hill offer books tailored to various levels of learning. These resources often come with detailed answers and explanations for better understanding.
Mobile Applications
Mobile apps can also be an excellent way to practice on the go. Apps like Wolfram Alpha, Brilliant, and Photomath offer real-time problem-solving support and allow you to work through problems at your own pace. Many apps provide visual aids and step-by-step guides that can help clarify complex concepts.
Tutoring Services
If you’re looking for more personalized guidance, tutoring services can provide focused help. You can find tutors through local education centers or online platforms like Chegg or Tutor.com. Working one-on-one with a tutor allows you to address specific challenges and receive tailored explanations and strategies.
Study Groups and Forums
Collaborating with others can be a helpful way to reinforce what you’ve learned. Study groups and online forums provide opportunities to share resources, solve problems together, and discuss difficult topics. Websites like Reddit, Stack Exchange, and StudyStack have communities dedicated to discussing math concepts and offering advice and feedback.