
In this section, we will explore a variety of materials designed to support learners in mastering key mathematical concepts. The content is structured to guide both students and educators through essential exercises, enhancing understanding and problem-solving skills. By using clear explanations and step-by-step guidance, students can confidently tackle complex problems and build a solid foundation for further study.
Focused practice is critical in reinforcing theoretical knowledge. This section provides an array of exercises and detailed solutions to ensure that every concept is well understood. Through hands-on learning and interactive approaches, learners can expect to improve their critical thinking and analytical abilities.
By engaging with these materials, both teachers and students can effectively track progress and address areas of difficulty. The comprehensive answers and explanations included ensure a complete learning experience, making this resource an invaluable tool for both instruction and independent study.
Mathematical Tools for Mastering Key Concepts
This section provides a variety of educational materials to help learners grasp important mathematical ideas effectively. With a focus on engaging activities and clear explanations, these materials aim to strengthen both understanding and problem-solving abilities. They are designed to make complex topics more accessible and to facilitate independent learning.
Through a well-structured approach, students can explore a wide range of practice exercises and detailed solutions. The tools are tailored to enhance critical thinking, allowing learners to improve their skills and confidently approach increasingly challenging problems. By offering practical support, this section helps build a strong foundation for future mathematical studies.
Effective support is essential for achieving success in mathematics. The materials provided allow students to track their progress, while educators can use them to identify areas where further attention is needed. With this comprehensive set of materials, learners are empowered to develop a deeper understanding and greater confidence in their abilities.
Overview of Chapter 9 in Mathematics

In this section, students will delve into advanced topics that build upon the foundational concepts covered earlier. The focus is on expanding problem-solving techniques and introducing more complex mathematical structures. As learners progress, they will encounter a range of new methods designed to enhance their understanding and ability to tackle intricate problems with confidence.
Key areas explored include:
- Understanding equations and their applications
- Solving multi-step problems involving variables
- Introduction to advanced problem-solving strategies
- Techniques for simplifying complex expressions
- Exploring mathematical relationships and patterns
The goal is to ensure students not only grasp the theoretical aspects but also develop practical skills that can be applied to real-world scenarios. This section provides the tools needed for mastering difficult problems, empowering learners to move forward in their studies with confidence.
Key Concepts Covered in Chapter 9
This section introduces a variety of important mathematical ideas designed to deepen understanding and improve problem-solving skills. The concepts explored here are essential for mastering advanced topics and are foundational for future mathematical studies. Learners will engage with a range of techniques that will enhance their ability to simplify, analyze, and solve complex problems with greater accuracy and confidence.
Equations and Their Solutions
One of the primary areas covered is solving equations involving multiple steps. This includes techniques for isolating variables and applying logical reasoning to find solutions. Students will learn to work with both linear and more advanced forms of equations, honing their skills to handle a variety of scenarios.
Mathematical Relationships and Expressions
In addition to solving equations, students will explore how mathematical expressions relate to one another. This includes simplifying and manipulating expressions to uncover hidden patterns, as well as solving problems that require a deeper understanding of these relationships.
Understanding Practice Exercises in Mathematics
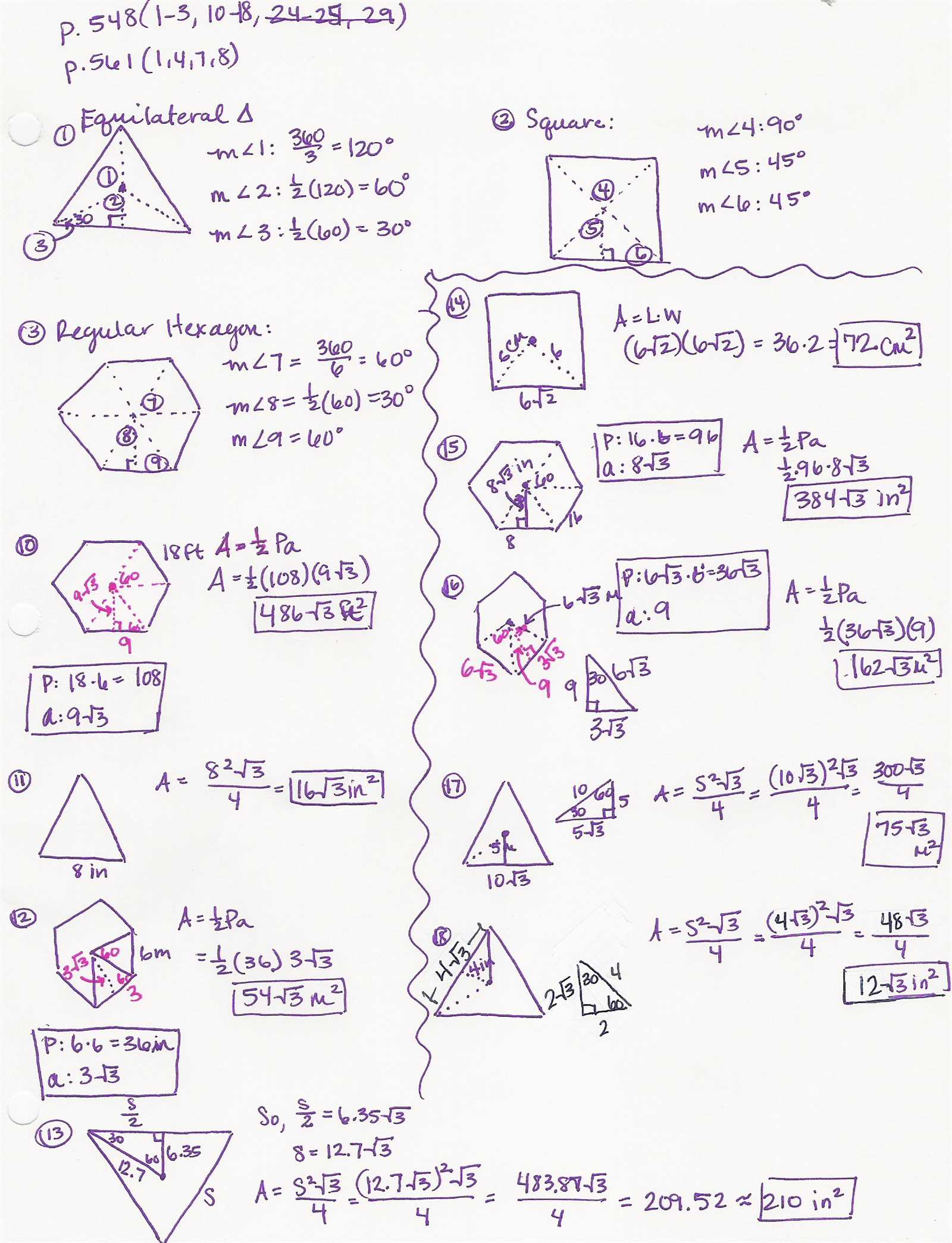
Practice exercises are essential for reinforcing the concepts learned in any mathematical field. They provide an opportunity for learners to apply theoretical knowledge to practical problems, improving their problem-solving skills and increasing confidence. By working through these exercises, students can better understand the key principles and become more proficient in solving complex problems.
Types of Practice Problems
The exercises vary in difficulty, with some focusing on basic calculations and others on more complex, multi-step problems. Each set is designed to gradually build skills, starting with simpler tasks and progressing to more challenging ones. By working through these problems, students will learn to identify patterns and apply strategies to arrive at the correct solutions.
Benefits of Regular Practice

Consistency in practice is crucial for mastery. Regularly engaging with exercises not only helps reinforce memory but also sharpens analytical thinking. As students work through different types of problems, they develop a deeper understanding of mathematical relationships and gain the ability to approach new challenges with a clear strategy.
Step-by-Step Solutions for Problems

In this section, we provide detailed, step-by-step solutions to some of the most challenging problems. These solutions are designed to help students understand the logical progression required to arrive at the correct answer. By breaking down each problem into manageable steps, learners can clearly follow the process and apply similar strategies to other questions.
Problem 1: Solving Multi-Step Equations
Let’s start with a multi-step equation. Here’s how to approach it:
| Step | Action |
|---|---|
| 1 | Distribute the constants across the parentheses. |
| 2 | Combine like terms on both sides of the equation. |
| 3 | Isolate the variable by adding or subtracting terms. |
| 4 | Divide both sides by the coefficient of the variable to solve. |
Problem 2: Simplifying Expressions
Next, we look at simplifying complex expressions. Here’s a breakdown of how to simplify an expression:
| Step | Action |
|---|---|
| 1 | Identify and combine like terms in the expression. |
| 2 | Apply the distributive property where necessary. |
| 3 | Factor any common terms to simplify further. |
By following these steps, students can gain clarity on how to break down and solve problems methodically, ensuring a deeper understanding of the material.
Effective Methods for Teaching Mathematics
To successfully guide students through complex mathematical topics, it is essential to adopt a variety of methods that cater to different learning styles. By combining traditional techniques with interactive and engaging approaches, instructors can foster a deeper understanding of the material and encourage active participation. The key is to provide clear explanations, consistent practice, and opportunities for students to apply their knowledge in meaningful ways.
Some of the most effective approaches include:
- Interactive Learning: Using hands-on activities and real-world applications helps students relate abstract concepts to practical scenarios.
- Collaborative Learning: Group work and peer discussions allow students to share insights and solve problems together, strengthening their understanding.
- Visual Aids: Diagrams, charts, and step-by-step guides can help illustrate complex ideas, making them more accessible to visual learners.
- Scaffolded Instruction: Breaking down problems into smaller, more manageable steps allows students to build confidence and master each part of the process.
Incorporating these methods into lessons ensures that students receive the support they need to thrive in their studies, helping them gain the skills necessary to solve problems with precision and confidence.
How to Use the Educational Materials
Effective use of educational materials can significantly enhance the learning experience. To make the most of the available tools, it’s important to integrate them strategically into lessons and activities. These materials are designed to support both students and instructors, providing structure, guidance, and opportunities for practice. When used effectively, they can help clarify concepts and reinforce key skills.
Here are some tips on how to make the most of the provided materials:
- Start with Clear Objectives: Before using any materials, outline the learning goals for the lesson. This will help you focus on the most relevant exercises and examples.
- Incorporate Practice Problems: Use exercises that progressively challenge students. Begin with simpler problems and gradually move to more complex ones to build confidence.
- Encourage Independent Work: Allow students to try problems on their own before discussing the solutions. This promotes critical thinking and problem-solving skills.
- Utilize Step-by-Step Guides: Provide students with detailed explanations for each problem. Break down complex steps to make sure they fully understand the process.
- Review and Reflect: After completing exercises, go over the solutions as a class. Encourage students to ask questions and discuss any areas of difficulty.
By following these steps, students can gain a deeper understanding of the material, and instructors can ensure that the educational tools are being used to their fullest potential, creating a more engaging and effective learning environment.
Answer Guide for Mathematics Problems
Having access to a comprehensive answer guide is an invaluable tool for both students and educators. It not only provides the correct solutions but also explains the reasoning behind each step, allowing learners to understand the methodology used to arrive at the final answer. This guide serves as a reference for those who need additional support and clarification when tackling complex problems.
How the Answer Guide Helps Students
For students, the guide offers a chance to verify their solutions and gain insight into the correct approach. By carefully reviewing the steps outlined in the guide, learners can identify areas where they may have gone wrong and improve their problem-solving techniques. Understanding the process behind each solution is key to mastering the material.
Effective Use of the Answer Guide

Proper use of the guide can enhance learning when students approach it after attempting the problems on their own. Rather than relying solely on the solutions, learners should engage with the guide to understand each step and reinforce their learning. Additionally, reviewing the guide in groups or with instructors can foster a deeper understanding and help clarify any lingering doubts.
Exploring Interactive Tools for Section 9

Interactive tools play a crucial role in enhancing the learning experience by allowing students to engage with the material in a dynamic way. These tools provide immediate feedback and help students visualize complex concepts, making abstract ideas more accessible. By incorporating interactive exercises, students can test their understanding, reinforce learning, and gain confidence in their abilities.
Some interactive tools that can be particularly helpful for mastering the material in this section include:
- Online Simulations: These tools allow students to manipulate variables and observe outcomes in real time, helping to reinforce key concepts.
- Interactive Quizzes: Quizzes with instant feedback help students gauge their understanding and identify areas that need further review.
- Graphing Tools: Software that allows students to graph equations and visualize functions can aid in better understanding relationships between variables.
- Step-by-Step Problem Solvers: Tools that break down each problem into manageable steps offer students a guided path to solving complex equations.
Using these tools, students can gain a deeper, more practical understanding of the material, which complements traditional learning methods and promotes a more engaging, hands-on approach to mastering new concepts.
Common Mistakes and How to Avoid Them
When tackling mathematical problems, it’s easy to make small errors that can lead to incorrect solutions. Identifying these common mistakes and learning how to avoid them is essential for improving problem-solving skills. Often, these errors stem from misunderstanding the process, rushing through calculations, or failing to follow the necessary steps in the correct order.
Here are some of the most frequent mistakes and tips on how to avoid them:
- Not Carefully Reviewing the Problem: Skipping the step of thoroughly reading the problem can lead to missing important details. Always take time to understand the question before starting.
- Incorrectly Applying Formulas: Misapplying formulas is a common error, especially when dealing with more complex problems. Double-check that you are using the right formula for the right type of problem.
- Sign Errors: Mistakes with positive and negative signs often occur when performing operations. Always keep track of signs, especially when dealing with subtraction or multiplication of negative numbers.
- Rushing Through Calculations: Speed can lead to simple calculation mistakes. Take your time to ensure each step is correct, and check your work as you go.
- Forgetting to Simplify: After reaching an answer, students sometimes forget to simplify their results. Always ensure that your final answer is in its simplest form, if necessary.
By being mindful of these common errors and adopting strategies to avoid them, students can increase their accuracy and confidence when solving problems.
Tips for Mastering Section 9
Mastering new mathematical concepts requires focus, practice, and the right strategies. Whether you’re tackling complex equations or working through problem-solving methods, understanding the key principles and applying effective study habits are essential to success. Here are some helpful tips for navigating through the material in this section and achieving mastery.
| Tip | How It Helps |
|---|---|
| Practice Regularly | Frequent practice helps reinforce concepts and improve retention. The more problems you solve, the more confident you become with the material. |
| Break Down Problems | Break larger problems into smaller, manageable steps to avoid feeling overwhelmed. This makes solving complex equations easier. |
| Review Mistakes | Learn from errors by reviewing your solutions. Understanding why you made a mistake helps prevent it in the future. |
| Seek Help When Needed | If you’re struggling with a concept, ask questions or seek clarification from a teacher, tutor, or study group. Don’t wait until the problem becomes bigger. |
| Use Visual Aids | Graphing and visualizing problems can provide a clearer understanding of relationships between variables and help you solve problems more effectively. |
By following these tips, you can build a solid foundation and develop the skills necessary to excel in this section. Consistent effort and the right strategies will lead to improved understanding and greater confidence when solving problems.
Importance of Review and Practice
Reviewing learned concepts and practicing problems regularly are fundamental for reinforcing knowledge and building long-term retention. Repetition allows students to become familiar with various problem-solving methods, making them more confident in their abilities and more efficient in applying learned techniques. Without consistent review, it’s easy to forget key information or become confused by new material.
Here are several reasons why regular review and practice are crucial:
- Improved Retention: Frequent practice helps solidify concepts in memory, making it easier to recall them during tests or assignments.
- Increased Speed and Accuracy: The more problems you solve, the faster and more accurately you can complete them, leading to better performance in exams and assignments.
- Confidence Boost: By reviewing and practicing regularly, students gain confidence in their understanding, which reduces anxiety when faced with new challenges.
- Identification of Weak Areas: Consistent review helps identify areas where more work is needed, enabling focused study on the concepts that require improvement.
- Mastery of Problem-Solving Techniques: Repeated practice leads to mastery of methods and strategies, ensuring that students can tackle problems efficiently.
By making review and practice an integral part of the learning process, students can greatly enhance their understanding and performance, leading to success in their academic endeavors.
Supplemental Materials for Algebra 1
Supplemental materials play a crucial role in reinforcing and expanding the knowledge gained through core lessons. These additional tools offer alternative methods for students to approach and understand complex topics, providing them with extra practice, visual aids, and step-by-step guidance. They can be particularly helpful for students who need further clarification or those looking to advance their learning beyond the standard curriculum.
Various types of supplementary materials can significantly enhance the learning experience:
- Practice Worksheets: Extra problem sets allow students to reinforce key concepts and practice applying methods, improving both speed and accuracy.
- Interactive Activities: Online exercises and interactive tools can offer immediate feedback, helping learners track their progress and focus on areas that need improvement.
- Video Tutorials: Visual explanations can make abstract concepts more accessible, breaking down difficult topics into manageable steps for better understanding.
- Study Guides: Comprehensive review materials that summarize key concepts and provide practice questions to help students prepare for exams.
- Solution Manuals: Detailed solutions to practice problems, showing the step-by-step process, can provide deeper insights into problem-solving strategies.
Incorporating these supplemental materials into daily study routines enables students to gain a more well-rounded understanding and better prepares them for success in their coursework.
Strategies for Solving Word Problems
Word problems can often be intimidating due to their real-world context and the need to translate textual information into mathematical equations. However, breaking down these problems into smaller, manageable steps can make them more approachable. By following a clear strategy, students can tackle word problems with confidence and accuracy.
Here are some effective strategies for solving word problems:
- Read the Problem Carefully: Start by reading the problem thoroughly to understand the situation. Pay attention to key details, such as quantities, relationships, and the question being asked.
- Identify Known and Unknown Values: Highlight or underline the given information and identify what you need to find. Assign variables to unknown quantities to make the problem easier to handle.
- Translate the Words into Mathematical Expressions: Convert the information into a mathematical form by identifying operations (addition, subtraction, multiplication, division) and relationships between the variables.
- Set Up an Equation: Use the relationships identified in the problem to write an equation or set of equations. Ensure that the equation reflects the conditions described in the word problem.
- Solve the Equation: Once the equation is set up, solve for the unknown variable(s) using appropriate mathematical techniques such as factoring, substitution, or elimination.
- Check Your Solution: After obtaining a solution, substitute it back into the original word problem to verify that it satisfies all the conditions and makes sense in the context of the problem.
- Interpret the Solution: Finally, ensure that the answer is properly interpreted in the context of the problem. Be sure to include units or labels where necessary and check for any reasonableness in the result.
By following these steps, students can develop a systematic approach to word problems, making even the most complex scenarios easier to understand and solve.
Improving Student Engagement in Algebra
Engaging students in mathematics can be a challenging task, particularly when the subject involves abstract concepts and complex problem-solving. However, fostering an interactive and dynamic learning environment can significantly enhance students’ interest and involvement. By incorporating a variety of strategies and tools, educators can make mathematical concepts more relatable and exciting for students.
Here are some approaches to boost engagement:
- Incorporate Real-World Applications: Show students how mathematical principles apply to everyday situations. Whether it’s calculating costs, analyzing data, or solving practical problems, connecting lessons to real-world contexts can make the subject more relevant and engaging.
- Utilize Technology: Interactive tools, such as educational apps, online games, and virtual whiteboards, can make learning more engaging. These resources help students visualize concepts and actively participate in lessons.
- Encourage Collaborative Learning: Group work and peer discussions allow students to share ideas and learn from each other. Collaborative activities, such as problem-solving challenges, foster a sense of community and make learning more interactive.
- Provide Instant Feedback: Offering immediate feedback helps students understand their mistakes and correct them in real time. This encourages a growth mindset and motivates students to continue improving.
- Use Differentiated Instruction: Tailoring lessons to accommodate various learning styles ensures that all students are engaged. Whether through visual aids, hands-on activities, or verbal explanations, addressing different needs can make learning more inclusive.
- Gamify the Learning Process: Turning learning into a game or competition can motivate students to participate actively. Rewards, points, and leaderboards can add an element of fun while reinforcing key concepts.
By employing these strategies, educators can create an environment where students feel motivated to engage with mathematical content and develop a deeper understanding of the subject matter.
Chapter 9 Assessment and Evaluation Tools
Effective evaluation tools are essential for measuring students’ understanding and mastery of key concepts. In this section, we explore a variety of methods to assess student performance and guide future instruction. These tools help instructors identify areas where students may need additional support and highlight areas of strength to build upon.
Types of Assessment Methods
There are several types of assessments that can be used to gauge student comprehension. These methods allow for both formative and summative evaluations, providing a comprehensive view of a student’s progress.
- Formative Assessments: These are ongoing evaluations that help instructors monitor student progress throughout the learning process. Examples include quizzes, group work, and classroom discussions.
- Summative Assessments: These assessments are typically administered at the end of a unit or course to evaluate overall student achievement. Final exams, standardized tests, and projects are common summative assessments.
- Peer Reviews: Peer assessment allows students to assess one another’s work, encouraging critical thinking and self-reflection. This method also promotes collaborative learning.
- Self-Assessments: Students reflect on their own learning by evaluating their performance and setting goals for improvement. This fosters greater ownership of the learning process.
Evaluation Criteria

To ensure assessments are effective, it is crucial to establish clear evaluation criteria. These criteria should focus on the key concepts and skills students are expected to master. The following table outlines typical evaluation aspects for different types of tasks:
| Task Type | Evaluation Focus | Assessment Criteria |
|---|---|---|
| Quiz | Knowledge retention and application | Accuracy, clarity, and completeness |
| Project | Problem-solving and creativity | Originality, problem-solving approach, and execution |
| Group Work | Collaboration and communication | Teamwork, participation, and presentation |
| Final Exam | Comprehensive understanding | Overall grasp of concepts, application, and analysis |
These evaluation tools provide a well-rounded approach to measuring student learning. By using multiple methods, instructors can better understand each student’s strengths and areas for improvement, leading to more targeted and effective instruction.
Resources for Teachers and Educators
Effective teaching requires a variety of tools and support materials to help instructors convey complex ideas clearly and engage students. In this section, we explore a range of materials that can assist educators in delivering high-quality lessons, providing assessments, and offering additional practice opportunities. These resources play a crucial role in enhancing student learning and improving instructional effectiveness.
Digital Tools and Platforms
Modern educators have access to a variety of digital tools that can help enhance their lessons and streamline the learning process. These platforms provide interactive content, instant feedback, and engaging activities for students. Below are some of the most popular digital tools:
- Interactive Learning Apps: Platforms like Kahoot, Quizlet, and Google Classroom allow for engaging quizzes, games, and assignments that help reinforce key concepts.
- Video Lessons: Websites such as YouTube and Khan Academy offer free video tutorials on a wide range of topics, making it easier for students to grasp difficult concepts.
- Virtual Whiteboards: Tools like Jamboard and Miro enable collaborative brainstorming, allowing students to work together on problems and share their thinking processes in real time.
Printed and Visual Materials
In addition to digital tools, traditional printed materials and visual aids remain important in supporting student learning. These materials can be used for in-class activities, homework assignments, and as supplementary resources. Some examples include:
- Worksheets and Practice Problems: Printed worksheets are an effective way for students to practice concepts independently, with immediate feedback from the teacher.
- Concept Maps and Diagrams: Visual aids such as flow charts, Venn diagrams, and timelines can help students understand complex ideas and relationships between concepts.
- Reference Guides: A well-organized reference guide or handbook provides students with quick access to key formulas, definitions, and problem-solving strategies.
By integrating both digital and traditional resources into the learning environment, educators can create a dynamic and supportive classroom experience that caters to diverse learning styles. These materials, when used strategically, can help students stay engaged and succeed academically.