Prentice Hall Gold Algebra 2 Chapter 3 Answer Solutions

In this section, we dive deep into the methods and techniques essential for solving complex mathematical problems. From equations to graphing strategies, understanding the core principles is key to mastering this topic. The focus is on providing clear, structured guidance for anyone tackling challenging problems that require more than basic knowledge.

Exploring various strategies is vital for finding efficient solutions. Whether it’s simplifying expressions, solving for unknowns, or analyzing equations, each approach helps build a stronger foundation for solving more advanced problems. The goal is to equip students with the tools to approach mathematical challenges with confidence.

With detailed solutions and step-by-step instructions, this guide will assist in navigating the more intricate aspects of the material. By following through with the examples provided, learners will not only solve the problems at hand but will also improve their problem-solving skills for future mathematical endeavors.

Mathematical Solutions and Key Insights

This section provides a comprehensive guide to understanding and solving problems in advanced mathematics. The material covered offers a deeper dive into the techniques and strategies needed to tackle complex exercises. With clear instructions and detailed explanations, learners can approach each problem with confidence and precision.

Within this guide, the focus is placed on:

• Breaking down equations and simplifying expressions
• Identifying key concepts and applying them effectively
• Using various methods to solve problems accurately
• Providing step-by-step solutions to ensure clarity

By studying these methods, students will enhance their ability to work through challenging problems and build a solid foundation for more advanced topics. The solutions provided are not just answers but tools to better understand mathematical reasoning and improve overall problem-solving skills.

The process involves:

1. Reviewing problem statements carefully to identify key elements
2. Applying the appropriate formulas and techniques
3. Double-checking solutions to ensure accuracy
4. Practicing with additional problems to reinforce learning

With these techniques, students will gain the confidence to handle increasingly complex topics and prepare effectively for tests and assessments.

Understanding Key Concepts of Chapter 3

This section is dedicated to exploring the fundamental principles that underpin the exercises in this unit. Mastering these core ideas is essential for successfully solving problems and advancing through the material. The goal is to provide a strong foundation that will enable students to tackle more complex topics with ease.

The key concepts covered include:

• Recognizing patterns and structures in mathematical problems
• Understanding how to manipulate and transform equations
• Identifying the significance of variables and constants in formulas
• Applying different strategies for solving for unknowns

Each concept is designed to be built upon, with later sections introducing more sophisticated techniques that rely on a solid grasp of these basics. By mastering these key ideas, learners will be equipped to approach problems methodically and accurately.

To further enhance understanding, it’s important to:

1. Practice identifying core concepts in each problem
2. Utilize graphical representations to clarify abstract ideas
3. Work through examples step-by-step to ensure comprehension
4. Test knowledge with similar problems to reinforce learning

By internalizing these concepts, students can build the confidence and skills needed to excel in more advanced mathematical topics.

Step-by-Step Guide to Problem Solving

Effective problem solving requires a clear, structured approach. By following a systematic process, students can break down complex problems into manageable steps and ensure that no detail is overlooked. This guide walks through the essential stages of solving mathematical problems, providing clarity and precision in every step.

1. Analyze the Problem

The first step is to carefully read the problem and identify the key components. Look for important information such as given values, unknowns, and what the problem is asking for. Highlighting these details will give you a clear roadmap of what needs to be solved.

2. Choose the Right Method

Once you understand the problem, the next step is to determine which mathematical methods or formulas to apply. This decision can depend on the type of equation or relationship involved. For example, if you’re solving for a variable, you may need to isolate it on one side of the equation. If dealing with a graph, consider plotting the data to visualize the relationship.

3. Break Down the Solution

Work through the problem step-by-step, making sure each calculation or transformation is logical and accurate. Simplify intermediate steps whenever possible to avoid errors. If necessary, check your work as you go along to catch mistakes early.

4. Verify Your Solution

Once you’ve arrived at a solution, it’s essential to verify that it makes sense in the context of the problem. Double-check all steps, re-interpret the original question, and see if the solution meets the conditions stated. Testing the solution in the original equation or scenario can often confirm its validity.

By following this methodical approach, students can improve their problem-solving skills and develop greater confidence in tackling complex challenges.

Common Mistakes and How to Avoid Them

When tackling complex mathematical problems, it’s easy to make mistakes that can lead to incorrect results. Being aware of common pitfalls and knowing how to avoid them is essential for achieving accuracy and mastering the material. This section highlights frequent errors and provides tips on how to prevent them.

Some of the most common mistakes include:

• Misunderstanding the problem – Not fully grasping what the question is asking can lead to the wrong approach. Always read the problem carefully and highlight key information.
• Sign errors – Mistakes with positive and negative signs often occur, especially when dealing with equations involving subtraction or multiplication. Double-check your work to avoid this mistake.
• Skipping steps – Rushing through steps can result in missed operations. Take your time and solve each step methodically to ensure consistency.
• Incorrectly applying formulas – Using the wrong formula or misapplying it is a common error. Always review the appropriate formulas before applying them to ensure they are suitable for the problem at hand.
• Not checking solutions – After finding a solution, it’s easy to assume the work is complete. Always verify your result by substituting it back into the original equation or context.

To avoid these mistakes, follow these best practices:

1. Carefully analyze the problem – Break down the question and identify what is being asked before proceeding with calculations.
2. Double-check each step – Revisit each calculation to ensure it is correct and consistent with the previous work.
3. Take your time – Avoid rushing through problems. A thorough and deliberate approach is often the key to avoiding errors.
4. Review your work at the end – Once you’ve completed the problem, take
   

   Reviewing Algebraic Techniques from Chapter 3

   In this section, we revisit the key mathematical techniques that form the foundation of solving the problems in this unit. Mastery of these methods is essential for progressing through more challenging material and developing a deeper understanding of mathematical reasoning. By reviewing these techniques, students can reinforce their knowledge and improve their problem-solving skills.

   Key Techniques to Remember

   The following techniques are critical to solving the exercises covered in this section:

   • Simplifying Expressions – Breaking down complex expressions into simpler forms by applying properties such as distributive and associative laws.
   • Factoring Equations – Recognizing patterns that allow for factoring, such as difference of squares or trinomials.
   • Isolating Variables – Rearranging equations to solve for unknowns by applying inverse operations.
   • Solving for Roots – Finding the roots of equations using various methods such as factoring, completing the square, or the quadratic formula.

   Tips for Applying These Techniques

   To ensure accurate application of these techniques, follow these steps:

   1. Understand the problem – Carefully read the problem to identify which technique is most appropriate for solving it.
   2. Work through each step logically – Avoid skipping steps, as this can lead to errors.
   3. Practice regularly – The more you practice applying these methods, the more intuitive and efficient they become.
   4. Review your work – After solving a problem, go back through the steps to check for mistakes or oversights.

   By continually reviewing and practicing these algebraic techniques, students can build a solid foundation for tackling more complex mathematical challenges in the future.

   How to Tackle Word Problems in Algebra

   Word problems can often seem daunting, but with the right approach, they become much easier to solve. The key is to translate the problem from words into mathematical expressions and equations. By breaking down the text and identifying important information, students can approach these problems step-by-step, making the process more manageable and less overwhelming.

   Follow these steps to effectively solve word problems:

   Step	Description
   1. Read the Problem Carefully	Understand the context and what the problem is asking. Identify key information like given values, relationships, and what needs to be found.
   2. Define Variables	Assign variables to the unknowns. This helps to organize the problem and makes it easier to write equations.
   3. Translate Words into Math	Convert the written relationships and operations into mathematical expressions (e.g., “sum” becomes “+”, “product” becomes “×”).
   4. Set Up the Equation	Formulate an equation or set of equations that represent the problem based on the information given.
   5. Solve the Equation	Apply algebraic techniques to solve for the unknowns, such as simplifying expressions and isolating variables.
   6. Check the Solution	Substitute your solution back into the original problem to ensure it makes sense and satisfies the conditions given in the text.

   By following these steps and practicing regularly, you can develop a systematic approach to solving word problems with confidence.

   Mastering Quadratic Equations in Algebra 2

   Quadratic equations are a fundamental concept in mathematics, appearing frequently in a variety of contexts. Mastering how to solve these equations is essential for progressing through more advanced topics. Quadratic equations typically involve variables raised to the second power, and they can be solved using multiple methods, each suited to different types of problems.

   There are several key methods to solve these equations:

   • Factoring: This method is effective when the equation can be factored into two binomials. By setting each factor equal to zero, the solutions can be found easily.
   • Completing the Square: This method involves rearranging the equation so that one side is a perfect square trinomial, making it easier to solve for the variable.
   • Using the Quadratic Formula: For equations that cannot be easily factored, the quadratic formula offers a reliable way to find the roots. The formula is:

   x = (-b ± √(b² – 4ac)) / 2a

   This formula works for any quadratic equation in the form of ax² + bx + c = 0, making it a powerful tool when other methods fail.

   Understanding when to apply each method is crucial. While factoring may be quicker for simpler equations, the quadratic formula provides a universal solution for more complex problems. By practicing each approach, you can become proficient in solving quadratic equations and strengthen your overall mathematical skills.

   Using Graphs to Solve Algebraic Equations

   Graphing is a powerful visual tool that can help solve mathematical equations by providing an intuitive representation of the relationship between variables. By plotting equations on a coordinate plane, you can identify the solutions more easily as the points of intersection with the x-axis (or other curves) correspond to the values that satisfy the equation. This method is especially useful for understanding the behavior of functions and finding approximate solutions to complex equations.

   To use graphs for solving equations, follow these steps:

   • Plot the equation: First, rewrite the equation in a form that is suitable for graphing, such as y = f(x) for functions or y = mx + b for linear equations. Then, plot the points on the coordinate plane based on the equation.
   • Identify the intersection points: The x-values where the graph crosses the x-axis represent the solutions to the equation. These are the points where y = 0 and the equation is satisfied.
   • Interpret the graph: For more complex equations, such as quadratics or higher-order polynomials, look for the points where the graph intersects the axis. These intersections are the values that solve the equation.

   By graphing equations and analyzing their intersections, you can quickly determine the solutions to many types of problems, especially when other algebraic methods are difficult or impractical to apply. With practice, graphing becomes a helpful tool for solving and visualizing mathematical relationships.

   Detailed Solutions for Complex Problems

   Complex mathematical problems often require a step-by-step approach to break them down into manageable parts. By carefully analyzing each component of the problem and applying the correct methods, you can simplify even the most challenging equations. Detailed solutions not only provide the correct answer but also help to understand the underlying principles that guide the process. This approach ensures that the reasoning is clear and that the problem-solving method is well understood.

   When solving more intricate problems, follow these guidelines to ensure clarity and accuracy:

   • Identify the problem type: Carefully read the problem to understand what is being asked. Determine whether the problem involves linear equations, systems of equations, quadratic functions, or other mathematical structures.
   • Break the problem into smaller parts: Complex problems often contain multiple steps. Begin by isolating the main operations required, such as simplifying expressions, factoring, or solving for specific variables.
   • Apply appropriate methods: Choose the correct technique based on the problem type. Whether it’s substitution, elimination, graphing, or using formulas, applying the right method is crucial for solving the equation efficiently.
   • Check your work: After obtaining a solution, substitute the values back into the original equation to verify correctness. Double-check each step to ensure no mistakes were made during the process.

   By following this detailed process, you can navigate complex problems with confidence, ensuring that both the steps and the solutions are correct. Understanding the reasoning behind each solution is essential for tackling even more difficult questions in the future.

   Essential Formulas to Remember for Algebra 2

   In advanced mathematics, memorizing key formulas is essential for solving a wide range of problems efficiently. These formulas serve as tools to simplify complex calculations and allow for quicker problem-solving. Whether working with functions, equations, or systems, knowing the correct formulas can save valuable time and help you avoid unnecessary mistakes.

   Here are some of the most important formulas to remember:

   Formula	Description
   Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a	Used to find the solutions of any quadratic equation in the form ax² + bx + c = 0.
   Factoring Formula: (a + b)(a – b) = a² – b²	Used for factoring the difference of squares, which is a common factorization method.
   Sum and Difference of Cubes: a³ – b³ = (a – b)(a² + ab + b²)	Helpful for factoring cubic expressions and simplifying cubic equations.
   Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²)	Used to calculate the distance between two points on a coordinate plane.
   Slope Formula: m = (y₂ – y₁) / (x₂ – x₁)	Used to find the slope between two points on a graph, which is essential in graphing linear equations.

   These formulas are fundamental for solving a variety of problems in advanced mathematics. Keeping them handy and practicing their application will make tackling problems much easier and more efficient.

   Exploring the Concept of Factoring

   

   Factoring is a crucial technique in mathematics that simplifies complex expressions into more manageable components. By breaking down an expression into its basic building blocks, factoring makes it easier to work with equations, solve problems, and understand the underlying structure of mathematical relationships. It is widely used in both solving polynomial equations and simplifying expressions in various areas of mathematics.

   Key Factoring Methods

   

   There are several methods of factoring, each tailored to different forms of mathematical expressions. The most commonly used methods include:

   • Greatest Common Factor (GCF): This method involves identifying the largest common factor among the terms of an expression and factoring it out, simplifying the overall equation.
   • Factoring Trinomials: When dealing with quadratic expressions, this method breaks down the trinomial into two binomials that, when multiplied, yield the original expression.
   • Difference of Squares: If an expression fits the form a² – b², it can be factored as (a + b)(a – b), known as the difference of squares.
   • Perfect Square Trinomials: When a trinomial is a perfect square, it can be factored into the form (a + b)² or (a – b)².

   Steps to Factor Successfully

   

   Factoring can be broken down into a systematic process that helps ensure accuracy. Follow these steps for effective factoring:

   1. Identify the type: Recognize whether the expression is a binomial, trinomial, or other polynomial type.
   2. Factor out the GCF: Always start by finding and factoring out the greatest common factor of the terms in the expression.
   3. Choose the right method: Depending on the form of the ex
      

      Important Strategies for Simplifying Expressions

      Simplifying expressions is a fundamental skill in mathematics that helps break down complex problems into more manageable forms. The goal is to make calculations easier by reducing the expression to its simplest possible version, often involving operations like combining like terms, applying distributive properties, or reducing fractions. Understanding how to simplify expressions efficiently can save time and lead to more accurate solutions, especially when working with polynomials, equations, and other mathematical constructs.

      Key Techniques for Simplification

      Here are several essential methods for simplifying expressions:

      • Combining Like Terms: One of the most straightforward ways to simplify an expression is by combining terms that have the same variable and exponent. This reduces the expression to fewer terms, making it simpler to manage.
      • Using the Distributive Property: The distributive property allows you to expand an expression by multiplying a term outside the parentheses by each term inside. This method is useful when simplifying expressions that involve parentheses.
      • Factoring Expressions: Factoring involves breaking down an expression into its component factors. This can simplify complex expressions, especially when dealing with polynomials or quadratic terms.
      • Applying Exponent Rules: Simplifying expressions that involve exponents can be achieved by using exponent laws, such as the product rule, quotient rule, and power rule. These help combine like terms with exponents or reduce powers to a simpler form.

      Steps to Effectively Simplify Expressions

      Follow these steps to ensure that you are simplifying expressions accurately:

      1. Identify Like Terms: Look for terms with the same base or variable raised to the same power, and combine them by addition or subtraction.
      2. Distribute Where Necessary: If the expression involves parentheses, apply the distributive property to remove the parentheses and simplify.
      3. Factor Complex Expressions: Factor out common terms or factor polynomials when possible to simplify the expression.
      4. Simplify Fractions: Reduce fractions by factoring the numerator and denominator and canceli
         

         How to Check Your Work in Algebra

         

         Double-checking your work is an essential skill in mathematics to ensure accuracy and avoid mistakes. It helps verify the correctness of your solutions by re-evaluating each step and looking for errors or oversights. Whether you are solving equations, simplifying expressions, or factoring polynomials, performing checks at various stages can lead to a more reliable result and increase your confidence in your problem-solving abilities.

         Methods to Verify Your Solutions

         

         Here are some strategies to help you check your work in mathematical problems:

         • Substitute Your Solution: One of the easiest ways to verify an equation is by substituting your solution back into the original equation. If both sides are equal, your solution is correct.
         • Reverse Operations: In some cases, you can reverse the operations used to simplify or solve an equation to check your work. For example, if you factored an expression, you can expand it back to see if you get the original form.
         • Estimate Your Answer: Before solving the problem, estimate what the answer should be. After solving, compare your answer to this estimate to ensure it falls within a reasonable range.
         • Break Down the Problem: If you find an error, review each individual step carefully. By isolating parts of the solution, you can identify where the mistake occurred and correct it.

         Using a Table to Check Your Work

         Sometimes organizing your steps in a table can help ensure that each part of the problem is covered and can be checked efficiently.

         Real-World Applications of Algebra 2

         The concepts learned in advanced mathematics are not confined to the classroom; they have numerous practical applications in various fields. From economics to engineering, the skills developed through solving equations, analyzing functions, and working with polynomials play a crucial role in addressing real-world challenges. Understanding these applications can highlight the importance of the subject and its relevance in everyday life.

         Applications in Engineering and Architecture

         In engineering and architecture, mathematical principles are essential for designing structures, calculating forces, and optimizing materials. For example, quadratic functions can be used to model the trajectory of objects or to design arches that distribute weight efficiently. Additionally, understanding how to solve systems of equations is vital in determining the most cost-effective and structurally sound solutions for building designs.

         Applications in Business and Economics

         In the business world, algebraic techniques are frequently used to analyze market trends, manage budgets, and make predictions. For instance, linear and quadratic models help in forecasting profits, analyzing costs, or predicting consumer behavior. Understanding how to manipulate these functions is essential for making informed decisions in finance, marketing, and operations management.

         Some common real-world problems that can be addressed with algebraic methods include:

         • Inventory Management: Using equations to track supply and demand, ensuring optimal stock levels.
         • Investment Analysis: Calculating returns on investments or determining loan payments and interest rates.
         • Optimization Problems: Maximizing profit or minimizing cost by analyzing different scenarios and constraints.

         Applications in Science and Technology

         Algebra also plays a significant role in fields such as physics, biology, and computer science. Whether it’s modeling population growth, analyzing data sets, or solving for unknown variables in scientific experiments, algebra is a foundational tool. For example, exponential functions are used to model radioactive decay, and systems of equations are essential in computer programming for solving complex algorithms.

         By recognizing the broad applications of these mathematical concepts, it becomes clear how they help solve practical problems and drive progress in various industries.

         Preparing for Tests and Quizzes in Algebra 2

         

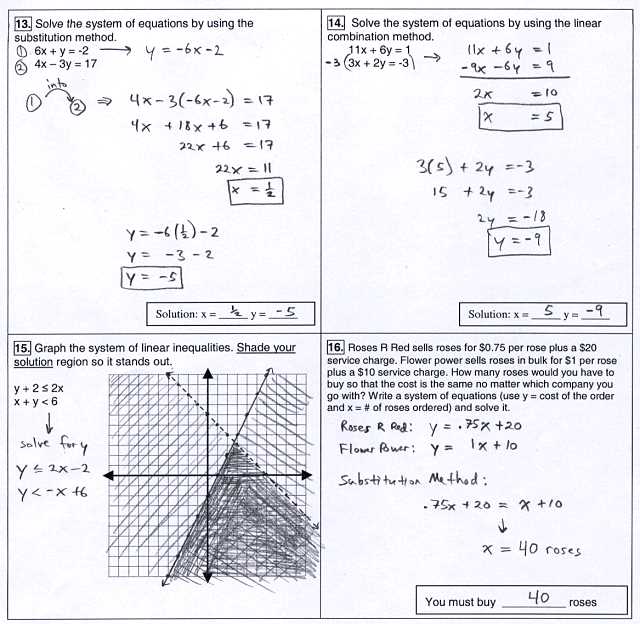
         Preparing for assessments in mathematics requires more than just reviewing notes–it involves a structured approach to understanding core concepts, practicing various types of problems, and ensuring you’re ready to apply what you’ve learned under test conditions. Effective preparation not only boosts confidence but also improves your ability to solve problems efficiently during exams.

         To maximize your success, consider the following strategies:

         • Understand Core Concepts: Ensure that you fully grasp the key ideas behind the topics covered. This understanding will allow you to solve problems more quickly and accurately, rather than relying on memorization.
         • Practice Regularly: The more problems you solve, the better you’ll get at recognizing patterns and applying the right methods. Focus on a mix of problem types to strengthen your overall problem-solving skills.
         • Review Mistakes: After working through practice problems, take the time to review any errors you made. Understanding where you went wrong will help prevent similar mistakes in the future.

         Additionally, managing your time effectively during your study sessions can make a significant difference. Create a study schedule, break down complex topics into manageable parts, and give yourself plenty of time to review difficult areas. The goal is to build both your understanding and your confidence.

         Effective Study Techniques

         • Active Problem Solving: Rather than simply reading through solutions, engage actively by solving problems yourself. Try to explain the reasoning behind each step as if you were teaching someone else.
         • Timed Practice: Simulate exam conditions by solving practice problems within a set time frame. This will help you manage your time effectively during the actual test.
         • Group Study Sessions: Collaborating with peers can provide new perspectives and help reinforce your understanding. Teaching each other difficult concepts is a great way to solidify your own knowledge.

         By staying organized, practicing consistently, and focusing on both strengths and weaknesses, you’ll be well-prepared to tackle any upcoming quizzes or tests confidently and effectively.

         Additional Resources for Algebra 2 Success

         To enhance your understanding and mastery of mathematical concepts, utilizing supplementary materials can be highly beneficial. Beyond textbooks and class notes, a variety of tools and platforms can offer extra practice, explain complex ideas in simpler terms, and allow for interactive problem-solving. By incorporating these resources into your study routine, you can strengthen your skills and improve your performance.

         Here are some valuable resources to consider:

         • Online Educational Platforms: Websites like Khan Academy and Coursera provide free, structured lessons on a wide range of topics. These platforms often break down concepts into manageable steps, making them easier to grasp and apply.
         • Interactive Graphing Tools: Tools such as Desmos and GeoGebra allow you to visualize equations and their transformations. These platforms provide a hands-on approach to understanding mathematical functions and their behaviors.
         • Problem-Solving Apps: Apps like Photomath and Wolfram Alpha can help you quickly solve equations and offer step-by-step explanations. These tools can also help you understand the reasoning behind each solution.
         • Textbooks and Workbooks: Many math publishers offer companion workbooks that provide additional exercises and practice problems. These can reinforce the material covered in class and give you the chance to apply concepts in different contexts.
         • Online Forums and Communities: Engaging with others in forums such as Stack Exchange or Reddit’s math community can provide insight and help when you’re stuck. These communities allow you to ask questions, share strategies, and learn from others’ experiences.

         Incorporating these resources into your study plan can provide different perspectives, practice opportunities, and clarification of difficult topics, helping you to achieve success in your coursework.

         Effective Ways to Utilize Resources

         • Stay Consistent: Regularly use supplementary resources to reinforce what you’ve learned in class. This consistency will help solidify your understanding of complex concepts.
         • Practice Actively: Don’t just read or watch explanations–engage with the material by solving problems and challenging yourself with new exercises. Active learning is crucial to mastering mathematical skills.
         • Ask for Help: If you’re struggling, seek assistance from tutors, teachers, or peers.

         Step	Action	Verification Method
         Step 1	Solve the initial equation or expression	Substitute the solution back into the equation