Calculus 1 Final Exam with Answers

Achieving success in mathematics often depends on a deep understanding of core principles and problem-solving techniques. Whether you’re preparing for a major assessment or looking to strengthen your grasp on critical topics, focusing on key areas can make all the difference. This guide is designed to help you navigate the essential concepts and sharpen your skills effectively.

Strategies and practice play a vital role in mastering the material. It’s important to approach challenges methodically, breaking them down into manageable sections. This approach not only builds confidence but also helps you understand the underlying connections between different ideas.

In this article, we will explore several important topics, providing clarity on complex problems and offering insightful techniques to solve them. By focusing on both the theoretical and practical aspects, you can enhance your problem-solving abilities and ensure you’re prepared for any challenge ahead.

Mathematics Assessment Preparation and Solutions

Preparing for a major mathematics assessment requires a structured approach to problem-solving and a thorough understanding of key topics. This section is designed to guide you through some of the most critical problems and techniques you’ll encounter, offering detailed solutions and strategies for each. Whether you’re reviewing for a big test or seeking to improve your skills, this guide will provide valuable insights to enhance your performance.

Key Problem Areas

To succeed in any challenging test, it’s important to recognize the areas where you may need extra focus. Common topics typically include:

• Limits and continuity
• Derivatives and their applications
• Integration techniques
• Optimization and related rates
• Graph analysis and interpretation

By reviewing these concepts carefully and practicing various problems, you can sharpen your ability to tackle even the most difficult questions confidently.

Effective Problem-Solving Techniques

Here are some essential strategies to keep in mind as you work through problems:

1. Understand the theory behind each concept before attempting to solve problems.
2. Break down complex problems into smaller, manageable steps.
3. Practice solving a variety of problems to ensure versatility in approach.
4. Pay attention to common mistakes, such as misapplying formulas or overlooking units of measurement.
5. Review detailed solutions to understand how each step fits together.

By consistently applying these techniques and reviewing solutions, you’ll improve your ability to solve problems quickly and accurately, helping you succeed in your mathematics studies.

Key Topics to Focus On

To excel in your assessment, it’s essential to concentrate on the core principles that underpin most problems. By honing in on the fundamental concepts, you’ll ensure a strong foundation that allows you to tackle a wide range of questions. Identifying the areas that are frequently tested can help you prioritize your study time and improve your problem-solving skills.

Understanding Limits and Continuity

Limits serve as the foundation for much of the material you’ll encounter. Gaining a solid understanding of how to calculate limits and identify discontinuities is critical. These concepts are key for solving more complex problems, such as derivatives and integrals. Focus on:

• Determining limits at infinity
• Handling indeterminate forms
• Identifying and addressing discontinuities

Mastering Derivatives and Applications

Derivatives are central to many mathematical tasks, including finding rates of change, slopes of curves, and solving optimization problems. Understanding the rules for differentiation and how to apply them in real-world scenarios is vital. Pay particular attention to:

• Power rule, product rule, quotient rule, and chain rule
• Applications in motion, growth, and decay problems
• Related rates and optimization problems

By focusing on these key topics, you will strengthen your problem-solving skills and improve your chances of success on your assessment.

Strategies for Effective Exam Preparation

Preparing for an important assessment requires more than just reviewing notes or memorizing formulas. A well-rounded strategy will not only help you grasp the essential concepts but also improve your ability to apply them under pressure. By focusing on smart study techniques and active problem-solving, you can significantly enhance your performance.

Start by organizing your study time efficiently. Break down your material into manageable sections and prioritize topics based on their importance and difficulty level. This approach ensures you give enough attention to areas that need more focus, while also reinforcing the concepts you’re already comfortable with.

Practice is key. Work through as many problems as you can, focusing on different types of questions to develop a versatile skill set. This will allow you to approach any problem with confidence, knowing you’ve encountered similar challenges before. Additionally, try simulating test conditions to improve your time management skills and reduce anxiety.

Lastly, make sure to review your solutions thoroughly. Understanding why a particular answer is correct (or incorrect) will deepen your understanding of the material and help you avoid similar mistakes in the future. Active review is just as crucial as active learning.

Commonly Tested Concepts in Calculus 1

When preparing for a significant assessment in mathematics, it’s important to focus on the key principles that are frequently tested. These foundational concepts form the core of most problems and understanding them deeply is crucial for success. Below are the essential topics that often appear in problems, and mastering them will help you navigate a wide range of questions confidently.

• Limits and Continuity: The concept of approaching a value is fundamental to solving many problems, especially when dealing with discontinuities and asymptotes.
• Derivatives: Derivatives are used to analyze rates of change and slopes of curves. Understanding their rules and applications, like the power rule, product rule, and chain rule, is essential.
• Optimization: These problems focus on finding maximum or minimum values, and often require setting up and solving equations involving derivatives.
• Integration: The process of integration, particularly techniques like substitution and integration by parts, is essential for solving area problems and evaluating antiderivatives.
• Application Problems: These include real-world scenarios such as motion, growth, decay, and related rates, which require both conceptual understanding and mathematical manipulation.

Focusing your study on these concepts will ensure you’re prepared for the most commonly tested areas and help you approach questions with a solid strategy.

Understanding Limits and Continuity

One of the foundational concepts in mathematics is the idea of approaching a value without necessarily reaching it. This principle is crucial for solving a variety of problems involving behavior near a specific point, especially when dealing with functions and their properties. A deep understanding of this concept is essential for working through more complex problems that require precise evaluation of function behavior in different contexts.

Continuity, closely related to limits, refers to whether a function behaves predictably as its input approaches a specific value. A function is continuous if small changes in the input result in small changes in the output, without sudden jumps or breaks. Recognizing and analyzing these behaviors forms the basis for many other mathematical tasks.

Condition	Meaning	Example
Limit Exists	The value a function approaches as the input gets closer to a particular point.	lim(x → 3) (x² – 9) / (x – 3) = 6
Continuity	A function is continuous at a point if it is defined at that point and the limit exists and equals the function’s value.	f(x) = x² is continuous at x = 2
Discontinuity	A function has a discontinuity at a point if it is not continuous there, often due to a jump or infinite behavior.	f(x) = 1 / (x – 1) has a discontinuity at x = 1

Mastering the concepts of limits and continuity allows you to understand the finer details of how functions behave, which is crucial for solving both theoretical and applied problems in mathematics.

​

Integrals and Fundamental Theorem of Calculus

The concept of accumulation plays a pivotal role in mathematics, particularly when analyzing how quantities change over intervals. The process of integrating allows us to calculate these accumulations, whether they represent areas, volumes, or other quantities. This section explores the connection between integrals and the fundamental principle that governs their computation, providing a foundation for more advanced applications.

The Role of Integration

Integration serves as the reverse of differentiation, where it sums up infinitely small contributions over a continuous domain. It allows for the calculation of various properties, such as the total area beneath a curve, by summing infinitesimal areas of infinitely small rectangles. This method leads to a powerful tool for understanding change and accumulation in real-world scenarios.

Connecting Derivatives and Integrals

The relationship between derivatives and integrals is formalized in the Fundamental Theorem of Calculus. This theorem establishes that integration and differentiation are essentially inverse operations. By applying this principle, we can evaluate integrals with much greater efficiency, using the antiderivative of a given function to compute total accumulation over a defined interval.

Solving Optimization Problems in Calculus

Optimization problems involve finding the best solution to a given situation, often by maximizing or minimizing a particular quantity. These problems are central to many areas of mathematics and its applications, including economics, engineering, and physics. The goal is to determine the conditions under which a quantity, such as cost, area, or volume, reaches its optimal value.

Steps to Solve Optimization Problems

To solve optimization problems, we typically follow a structured approach that involves several key steps:

Step	Description
1. Define the objective	Identify the quantity to be maximized or minimized, such as area, volume, or profit.
2. Express the objective function	Write the function that represents the quantity to be optimized in terms of the variables involved.
3. Find critical points	Differentiate the objective function and solve for the points where the derivative is zero or undefined.
4. Test the critical points	Use the second derivative test or other methods to determine whether the critical points correspond to maxima or minima.
5. Interpret the results	Analyze the solution in the context of the problem and check for any constraints that may affect the optimal value.

Working with Related Rates Questions

Related rates problems involve finding the rate of change of one quantity in relation to another. These questions often arise in real-world scenarios where multiple variables are changing over time. By using the chain rule, we can connect these changing quantities and solve for unknown rates of change in different contexts, such as motion, growth, and physical phenomena.

Steps to Solve Related Rates Problems

To approach a related rates problem, follow these essential steps:

1. Identify all given quantities: Determine the known values, including any rates of change, and what needs to be found.
2. Write an equation connecting the variables: Find a relationship between the variables involved in the problem.
3. Differentiate with respect to time: Use implicit differentiation to relate the rates of change of the variables.
4. Solve for the unknown rate: Substitute the known values and solve for the desired rate of change.
5. Check the units: Ensure that the units for each rate make sense in the context of the problem.

Example of a Related Rates Problem

Consider a problem where a balloon is being inflated, and we need to determine how fast the radius is increasing when the volume of the balloon is changing at a certain rate. The relationship between the radius and volume of a sphere is given by the formula:

• Volume of a sphere: ( V = frac{4}{3} pi r^3 )

To find the rate of change of the radius, differentiate this equation with respect to time and apply the given information to solve for the unknown rate.

Antiderivatives and Integration Techniques

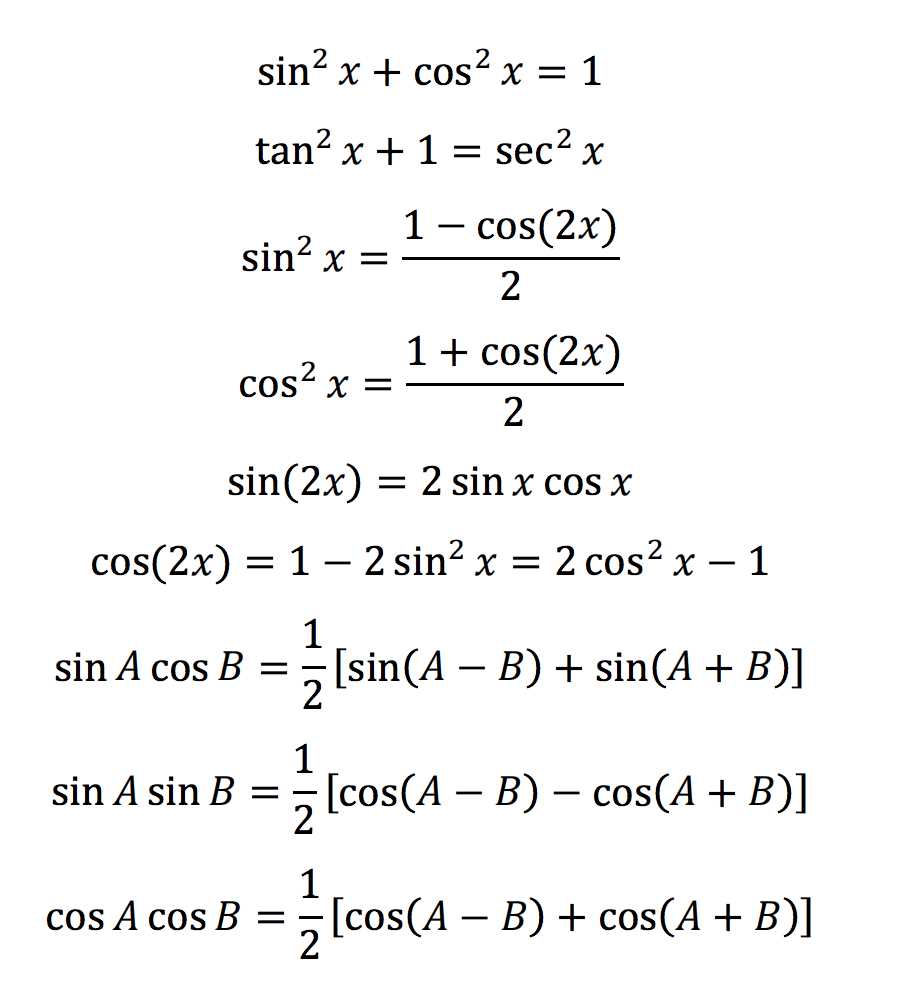
In mathematics, finding the reverse of differentiation is crucial for solving problems involving accumulation and area. The process of determining the original function from its derivative is known as finding antiderivatives. Various methods are employed to tackle these problems, allowing for the calculation of integrals in a range of different scenarios, from simple to complex functions.

Basic Antiderivatives

The most fundamental technique for finding antiderivatives involves recognizing standard forms and applying basic rules. For example, the antiderivative of a power function, such as ( x^n ), is given by the formula ( frac{x^{n+1}}{n+1} ), provided that ( n neq -1 ). Other common forms include trigonometric and exponential functions, each with their own specific rules for integration.

Advanced Integration Techniques

For more complicated integrals, several advanced methods can be employed, including substitution, integration by parts, and partial fractions. Each technique is designed to simplify the integral into a form that is easier to solve. Substitution involves changing variables to simplify the integrand, while integration by parts breaks down the product of functions into manageable parts. In the case of rational functions, partial fraction decomposition allows the expression of a complex fraction as a sum of simpler fractions.

Tips for Tackling Word Problems

Word problems require translating a real-world scenario into a mathematical form that can be solved. They often present complex situations with various variables, and the key to solving them is to break them down step-by-step. By carefully interpreting the given information and choosing the right mathematical approach, even challenging problems can be solved effectively.

Approach to Solving Word Problems

Here are some tips to guide you through solving word problems:

Step	Description
1. Understand the problem	Read the problem carefully, identify the given information, and figure out what is being asked.
2. Define variables	Assign symbols or letters to represent unknown quantities or variables in the problem.
3. Write an equation	Translate the word problem into an equation or system of equations based on the relationships between the variables.
4. Solve the equation	Use appropriate techniques, such as substitution or elimination, to solve for the unknowns.
5. Interpret the solution	Ensure that the solution makes sense in the context of the problem and check if the units and conditions are correct.

Reviewing Common Mistakes on Exams

Understanding the most frequent errors made during assessments can help improve performance and avoid pitfalls. These mistakes often stem from misinterpretations of the problem, incorrect application of methods, or careless algebraic errors. By identifying and addressing these issues, one can approach similar tasks with greater confidence and accuracy in the future.

Common Mistakes to Avoid

• Misreading the question: Carefully read each question and ensure that you understand what is being asked before attempting to solve it.
• Not showing work: Leaving out steps in your calculations can lead to errors, and it is often necessary for partial credit even if the final answer is wrong.
• Sign errors: Watch out for negative signs, especially when working with functions or derivatives where signs change throughout the problem.
• Skipping units: Always include units when necessary and make sure that they are consistent throughout the problem to avoid confusion.
• Overcomplicating the solution: Sometimes problems are simpler than they appear–look for the most straightforward approach before resorting to complex methods.

How to Analyze Graphs in Calculus

Analyzing graphs is a critical skill when studying mathematical functions and their behaviors. By examining the shape, slopes, and key features of a graph, you can gather valuable insights about the function’s properties, such as increasing or decreasing intervals, critical points, and inflection points. Proper analysis helps in understanding the overall trends and making accurate predictions based on the graph’s visual representation.

Key Elements to Look for in Graphs

• Intercepts: Identify where the graph crosses the axes. These points indicate where the function equals zero or where its value is undefined.
• Critical points: Look for points where the graph changes direction, typically where the slope is zero or undefined. These points can represent local maxima, minima, or saddle points.
• Intervals of increase and decrease: Determine where the graph is rising or falling by examining the slope of the curve. A positive slope indicates increasing behavior, while a negative slope indicates decreasing behavior.
• Concavity and inflection points: Analyze the curve’s concavity to determine whether it is curving upwards or downwards. Inflection points occur where the concavity changes.
• Asymptotes: Check for vertical, horizontal, or slant asymptotes that indicate the behavior of the function as it approaches certain values or infinity.

Steps for Effective Graph Analysis

1. Step 1: Identify key points such as intercepts and critical points.
2. Step 2: Examine the behavior of the graph between critical points to determine intervals of increase or decrease.
3. Step 3: Assess the concavity and locate any inflection points where the graph changes curvature.
4. Step 4: Check for asymptotes and note any behavior as the function approaches infinity or specific values.
5. Step 5: Combine all information to understand the overall shape and trends of the graph.

Important Formulas and Theorems to Memorize

Mastering key formulas and theorems is essential for solving mathematical problems efficiently. These tools are often used to simplify complex calculations and provide foundational understanding in various topics. By memorizing these essential formulas and theorems, you will be better equipped to tackle a wide range of mathematical challenges.

Essential Formulas

• Power Rule: The antiderivative of ( x^n ) is ( frac{x^{n+1}}{n+1} ) (for ( n neq -1 )).
• Chain Rule: If ( y = f(g(x)) ), then ( frac{dy}{dx} = f'(g(x)) cdot g'(x) ).
• Product Rule: If ( y = u(x) cdot v(x) ), then ( frac{dy}{dx} = u'(x) cdot v(x) + u(x) cdot v'(x) ).
• Quotient Rule: If ( y = frac{u(x)}{v(x)} ), then ( frac{dy}{dx} = frac{v(x) cdot u'(x) – u(x) cdot v'(x)}{[v(x)]^2} ).
• Fundamental Theorem of Integration: If ( F(x) ) is the antiderivative of ( f(x) ), then ( int_{a}^{b} f(x) , dx = F(b) – F(a) ).

Key Theorems

• Mean Value Theorem: If a function is continuous on ( [a, b] ) and differentiable on ( (a, b) ), there exists at least one point ( c ) in ( (a, b) ) such that ( f'(c) = frac{f(b) – f(a)}{b – a} ).
• Intermediate Value Theorem: If a function is continuous on ( [a, b] ), then for any value between ( f(a) ) and ( f(b) ), there exists at least one point ( c ) in ( [a, b] ) such that ( f(c) ) equals that value.
• L’Hopital’s Rule: If a limit results in an indeterminate form ( frac{0}{0} ) or ( frac{infty}{infty} ), then ( lim_{x to c} frac{f(x)}{g(x)} = lim_{x to c} frac{f'(x)}{g'(x)} ), provided the
  

  Using Calculator Efficiently During the Exam

  Maximizing the utility of your calculator can significantly enhance your problem-solving speed and accuracy. By familiarizing yourself with its functions and using it strategically, you can save time and avoid unnecessary errors. It’s essential to know when to rely on manual calculations and when to use the calculator for more complex computations, ensuring that it complements your understanding of the material.

  Tips for Efficient Calculator Use

  • Understand the Calculator Functions: Before the test, familiarize yourself with the various features of your calculator, such as graphing, solving equations, and working with matrices, so you can quickly access them when needed.
  • Use Graphing Capabilities: For problems involving curves, critical points, or intervals, use the graphing function to visually interpret the behavior of the function and verify your solutions.
  • Break Down Complex Calculations: For long or complicated expressions, input the terms step by step. This reduces the risk of input errors and helps you track the calculations more easily.
  • Double-Check Results: Always review the output generated by your calculator. While it can be a time-saver, relying solely on it without understanding the process may lead to mistakes.
  • Use the Memory Function: If your calculator allows storing values in memory, use this feature to keep track of intermediate results and avoid repeating calculations.

  Time Management for the Final Exam

  Effective time management is crucial when approaching a high-stakes assessment. By allocating time wisely, you can ensure that you have enough opportunity to carefully address each problem while avoiding unnecessary stress. Proper planning allows you to focus on the areas that require more attention and leave room for reviewing your work at the end.

  Strategies for Managing Your Time

  • Read Through the Entire Test: Before starting, quickly skim through the entire assessment to get a sense of the types of questions and their difficulty. This helps you allocate time for each section based on its complexity.
  • Start with What You Know: Begin by tackling the questions you feel most confident about. This will help build momentum and boost your confidence for more challenging tasks.
  • Time Each Section: Divide your time based on the number of questions or sections. If a section is worth more points, allocate more time to it.
  • Avoid Getting Stuck: If you encounter a difficult question, don’t spend too much time on it. Mark it, move on, and return to it later if you have time left.
  • Leave Time for Review: Always reserve a few minutes at the end to go back and check your work for any mistakes or missed steps.

  Time Allocation Table

  

  Section	Suggested Time (Minutes)	Tips
  Introduction/Short Questions	10-15	Quickly answer these to gain confidence and move on to longer sections.
  Medium Difficulty Problems	30-40	Allocate sufficient time for these, but don’t get stuck for too long on one problem.
  Harder Problems/Essay-type	45-60	Focus on the most challenging questions when your mind is fresh. Don’t rush.
  Review	10-15	Check for any missed steps, mistakes, or incomplete answers.

  Exam Day Tips and Mental Preparation

  The key to success on assessment day is a combination of preparation and maintaining a calm, focused mindset. Knowing how to approach the day, managing your stress, and staying mentally sharp can make a significant difference in your performance. Establishing a strategy that balances relaxation and concentration will help you approach each task with clarity and confidence.

  Preparing Mentally

  • Get Enough Rest: Ensure you have a good night’s sleep before the test. Being well-rested improves cognitive function and concentration.
  • Stay Calm: Anxiety can negatively affect performance. Practice deep breathing or mindfulness techniques to stay relaxed.
  • Positive Visualization: Visualize yourself succeeding. Imagine walking through the test confidently and successfully solving each problem.
  • Eat a Healthy Breakfast: A nutritious meal boosts energy levels and helps maintain focus throughout the day.

  On the Day of the Test

  

  • Arrive Early: Get to the testing location early to avoid unnecessary stress. This gives you time to settle in and mentally prepare.
  • Bring Necessary Materials: Ensure you have everything you need, such as your calculator, pencils, identification, and any allowed reference materials.
  • Stay Hydrated: Drink water to keep your body and mind functioning at their best. Dehydration can affect concentration and problem-solving abilities.
  • Read Instructions Carefully: Before diving into problems, read all the instructions to avoid mistakes and understand what is being asked of you.

  Post-Exam Review and Understanding Mistakes

  

  After completing an assessment, reviewing your performance is a critical step in the learning process. Analyzing the mistakes you made helps identify areas for improvement and reinforces your understanding of the material. This reflection not only enhances your knowledge but also prepares you for future challenges by turning errors into valuable learning opportunities.

  Steps to Effectively Review Your Performance

  • Identify Mistakes: Go through your work carefully and pinpoint where you made errors. Understanding the nature of these mistakes is the first step to improving.
  • Understand Why: For each mistake, ask yourself why you made it. Was it due to a lack of understanding, a miscalculation, or time pressure? Identifying the cause helps prevent similar errors in the future.
  • Seek Clarification: If you’re unsure why something went wrong, review the relevant material or ask an instructor or peer for clarification. Gaining a deeper understanding will help you correct future mistakes.
  • Practice Similar Problems: Once you identify areas for improvement, practice additional problems that focus on these concepts. Repetition solidifies understanding and builds confidence.
  • Reflect on Time Management: Consider whether you spent too much time on certain questions or rushed through others. Improving your time management can lead to better performance next time.