Calculus AB Final Exam Tips and Study Guide

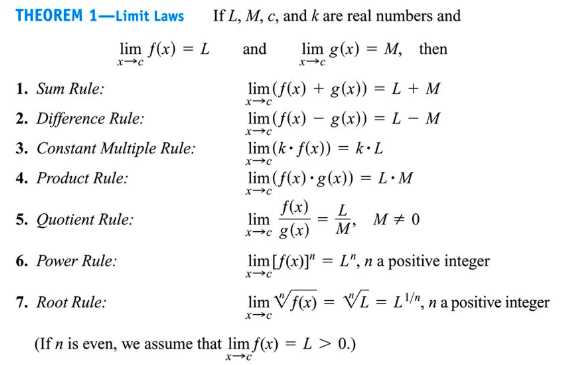
Mastering advanced mathematical concepts requires more than just memorization–it demands a deep understanding and the ability to apply theory in various scenarios. For students facing an important evaluation in this subject, it’s crucial to develop a strategy that focuses on both the fundamentals and more complex topics. With a strategic approach, success becomes not only attainable but expected.

Reviewing key topics and practicing problem-solving are essential to achieving high performance. Focusing on the areas that are most frequently tested, while ensuring you understand their underlying principles, will provide a strong foundation. Identifying your weaknesses early and addressing them will give you an edge on the big day.

Approaching the test with confidence comes from knowing the material inside and out. However, it’s also important to practice time management and be prepared for the variety of challenges the assessment may present. Whether it’s algebraic manipulation or applying geometric principles, familiarity with the types of questions and how to tackle them will significantly reduce anxiety and improve your performance.

Ultimate Guide to Advanced Mathematics Assessment

Achieving success in advanced mathematics requires more than just mastering isolated topics. It’s about connecting the concepts and building a comprehensive understanding that will help you tackle any challenge on the test. This guide will provide you with essential strategies, resources, and tips to confidently approach your evaluation and perform at your best.

Understanding the core components of the subject is the first step in preparation. By focusing on both theory and practical problem-solving, you’ll be able to navigate the most common types of questions with ease. Here’s how to structure your study plan:

Review Key Concepts – Begin with the foundational principles that are essential to the subject. Make sure you’re comfortable with topics like limits, derivatives, and integrals.
Practice Regularly – Solve practice problems consistently to reinforce your understanding and improve your problem-solving skills.
Understand Application – Focus on how abstract theories are applied to real-world scenarios. This will help you with word problems and practical applications.
Simulate the Test – Take practice tests under timed conditions to improve your speed and efficiency.

One of the most effective ways to ensure thorough preparation is to use a variety of study materials. Different resources can provide new perspectives and different types of questions, which will help you prepare for any challenge that may arise. Consider the following:

Textbooks and study guides that cover all essential topics.
Online platforms that offer practice tests and interactive quizzes.
Study groups or tutoring sessions for collaborative learning and clarification of doubts.

Finally, remember that managing your time is key. The ability to quickly identify the most efficient methods for solving problems will save you precious minutes on the assessment. Staying calm, focused, and organized throughout your preparation and during the test will give you a distinct advantage.

Understanding the Assessment Structure

To succeed in any evaluation, it’s crucial to know its structure inside and out. The assessment for this subject is divided into multiple sections, each designed to test different aspects of your mathematical understanding. By familiarizing yourself with how the questions are organized, you can approach each part of the test with confidence and efficiency.

The overall structure includes both multiple-choice and free-response questions. Each section focuses on different skill sets, from applying theories to solving complex problems, and requires a different approach. Knowing what to expect will help you allocate time and energy effectively during the test.

Here is a breakdown of the main components:

Multiple-Choice Section – This part tests your ability to recognize and apply concepts quickly. It typically includes 45 questions, and you’ll need to choose the correct answer from a set of options.
Free-Response Section – This section requires you to show your work in a series of open-ended questions. You will need to explain your reasoning clearly, demonstrating a deep understanding of the material.
Time Allocation – The multiple-choice section is given a specific time limit, usually shorter than the free-response section. Planning your time for each part is essential to complete the test effectively.

Understanding how the assessment is divided will help you prioritize your preparation and ensure that you are ready for all sections of the test. With this knowledge, you can focus your efforts where they are most needed and approach the day with a strategy in mind.

Key Concepts to Focus On

In any advanced mathematics assessment, understanding the key principles that form the foundation of the subject is essential. By concentrating on the most crucial topics, you can ensure that you have a solid grasp of the material and are able to apply it effectively in various problem-solving scenarios. Some of the core areas you should prioritize during your study sessions include limits, derivatives, integrals, and their real-world applications.

The following table outlines the key concepts and their importance in the assessment:

Concept	Importance
Limits	Understanding limits is crucial as they form the basis for many other topics, including derivatives and integrals. Mastery of this concept is necessary for evaluating functions at specific points.
Derivatives	Derivatives represent the rate of change of a function and are essential for solving problems related to motion, optimization, and related rates.
Integrals	Integrals are used to calculate areas under curves and accumulated quantities. A strong understanding of integration techniques is essential for solving a wide range of problems.
Applications of Derivatives and Integrals	Being able to apply derivatives and integrals to real-life scenarios such as motion, area, and volume problems is a critical skill for success.
Series and Sequences	Recognizing patterns in sequences and using series expansions is important for understanding more complex concepts and solving advanced problems.

Focusing on these key areas will provide you with the essential knowledge needed to succeed. Make sure to spend extra time on areas where you feel less confident, as these are often the most challenging and can significantly impact your overall performance. By mastering these concepts, you will be well-equipped to tackle a variety of problem types with ease.

Effective Study Techniques for Success

To succeed in any challenging mathematical assessment, it’s essential to approach your study sessions with a clear plan and focus. Effective study techniques not only enhance your understanding of the material but also help you retain and apply concepts under pressure. By using proven strategies, you can optimize your study time and improve your performance significantly.

Here are some of the most effective study methods to incorporate into your preparation:

Active Learning – Engage with the material actively by solving problems rather than passively reading through notes. This helps reinforce concepts and improves retention.
Practice Problems – Regularly solve practice problems to apply theoretical knowledge to real-world scenarios. Focus on problems that challenge your understanding and provide feedback.
Spaced Repetition – Review material multiple times over a longer period, gradually increasing the interval between each session. This helps improve long-term memory.
Group Study – Collaborating with peers can help clarify difficult concepts and offer new perspectives. Group study sessions are especially useful for discussing complex problems and sharing techniques.
Teach Someone Else – Explaining concepts to someone else is an excellent way to reinforce your understanding. If you can teach a topic clearly, you have truly mastered it.

In addition to these techniques, time management is essential for effective studying. Break your study sessions into manageable chunks and take regular breaks to avoid burnout. For example, using the Pomodoro Technique–studying for 25 minutes, then taking a 5-minute break–can help maintain focus and energy levels.

By incorporating these strategies into your routine, you’ll be able to study more efficiently, improve your understanding, and ultimately perform better during the assessment.

Common Mistakes to Avoid

In any challenging assessment, there are several pitfalls that can undermine your performance, even if you’ve studied thoroughly. Recognizing and avoiding common mistakes can make a significant difference in your results. Whether it’s misinterpreting a question or neglecting key concepts, small errors can add up quickly and impact your overall score. By being aware of these common issues, you can approach your preparation and the test itself with greater focus and accuracy.

Misunderstanding the Problem

One of the most frequent mistakes students make is rushing through questions without fully understanding them. Often, the wording of a problem can be tricky, and a hasty approach leads to misinterpretation. Always take a moment to carefully read each question and identify what is being asked. If needed, break the question into smaller parts and ensure you understand the context before attempting a solution.

Neglecting to Show Work

Another common error is failing to show all the steps in problem-solving. In open-ended questions, not demonstrating your process can lead to lost points, even if the final answer is correct. Remember, it’s just as important to communicate your reasoning as it is to get the correct result. Always write out your steps clearly and double-check that you haven’t skipped any crucial calculations or assumptions.

Avoiding these mistakes will help you increase your accuracy and ensure that you can confidently tackle each part of the test. With careful attention to detail and a thoughtful approach, you can minimize errors and boost your chances of success.

How to Manage Assessment Time

Effective time management during an important evaluation is essential to performing at your best. It’s not enough to simply know the material; you must also be able to pace yourself and allocate time wisely to ensure you can complete every section. By planning ahead and staying organized throughout the test, you can avoid rushing through questions and maintain control over your performance.

Here are some key strategies to help you manage your time effectively:

Read the Instructions Carefully – Before diving into the questions, spend a few minutes reading the instructions. This will ensure you understand what’s required and prevent unnecessary mistakes.
Estimate Time per Question – Look at the total time available and estimate how much time you should spend on each section. For example, allocate more time to complex problems and less to simpler ones.
Prioritize the Easy Questions – Start with the questions you find easiest or are most confident in. This will boost your confidence and allow you to secure quick points early on.
Don’t Get Stuck – If you encounter a difficult problem, don’t waste too much time on it. Mark it and move on to the next one. Come back to it later if time permits.
Monitor Your Progress – Keep an eye on the time as you go through the test. Set specific time checkpoints to ensure you’re staying on track and have enough time to address all sections.

By using these strategies, you’ll be able to stay calm, focused, and in control throughout the entire assessment. Proper time management ensures you can thoughtfully approach each question without feeling rushed, which can ultimately lead to a stronger performance.

Tips for Mastering Integration

Mastering the process of integration is crucial for tackling a wide variety of problems in advanced mathematics. Whether you are dealing with areas under curves or solving differential equations, the ability to integrate effectively is a skill that can significantly enhance your problem-solving capabilities. With consistent practice and a strong understanding of the core principles, you can simplify even the most complex integrals and apply them confidently in different scenarios.

Here are some valuable tips to help you master integration:

Understand the Fundamental Concepts – Before attempting complex problems, make sure you have a strong grasp of the basic principles of integration. Familiarize yourself with different types of integrals and their properties, such as definite and indefinite integrals.
Practice Basic Integration Rules – Reinforce your understanding by practicing common integration techniques like the power rule, substitution, and integration by parts. These foundational tools will help you tackle more complicated problems as you progress.
Master Substitution Method – The substitution method is a powerful tool for simplifying integrals. Practice recognizing when to use substitution and how to choose the appropriate substitution to make the integral more manageable.
Learn Integration by Parts – This technique is especially useful when dealing with products of functions. Make sure to practice various problems where integration by parts is the most efficient method.
Utilize Special Integrals – Certain types of integrals, such as trigonometric, exponential, and logarithmic functions, have specific rules and shortcuts. Familiarize yourself with these special cases and their integration techniques.
Work on Word Problems – Applying integration to real-world problems helps solidify your understanding. Focus on problems involving areas, volumes, and accumulation, as they often require a solid understanding of how integration applies in practical contexts.

With dedication and consistent practice, you can sharpen your integration skills and approach more complex mathematical problems with confidence.

Mastering Limits and Continuity

Understanding the behavior of functions as they approach specific points is fundamental to solving many advanced mathematical problems. Limits and continuity provide the groundwork for concepts like derivatives and integrals. By mastering these principles, you gain the ability to analyze functions in greater depth, which is essential for tackling complex problems in various mathematical fields.

Here are some key strategies to help you master limits and continuity:

Grasp the Concept of Limits – Limits describe the behavior of a function as it approaches a particular point. Start by understanding the basic definition and work through simple examples to get a feel for how limits are calculated.
Learn Different Types of Limits – Explore one-sided limits, infinite limits, and limits at infinity. Each type of limit has its own set of rules and applications, so it’s essential to recognize the differences and practice accordingly.
Understand Continuity – A function is continuous if its graph has no breaks, jumps, or holes. Practice determining whether a function is continuous at a given point by checking if the limit exists and if the function is defined at that point.
Use Limit Laws – There are several useful limit laws that simplify the calculation process, such as the sum, product, and quotient laws. Familiarize yourself with these laws and apply them in different scenarios to make calculations more efficient.
Work Through Real-World Examples – Applying limits and continuity to real-world problems helps solidify your understanding. Focus on how these concepts are used in physics, economics, and engineering to model real-life situations.

By mastering limits and continuity, you build a solid foundation for understanding more advanced topics. Regular practice with a variety of functions will deepen your comprehension and prepare you for tackling even the most challenging problems.

Derivatives and Their Applications

The study of how functions change in response to small variations in their inputs is central to understanding a wide range of mathematical and real-world problems. Derivatives provide the tools to analyze rates of change, whether it’s the speed of an object, the growth of a population, or the optimization of a process. By mastering the concept of derivatives, you gain the ability to model and solve problems across various fields of study.

Understanding the Basics of Derivatives

At its core, a derivative represents the rate of change of a function at any given point. It is a powerful tool for understanding how a function behaves and for predicting future outcomes based on its current state. The process of differentiation can be applied to a wide variety of functions, and it is essential to understand the basic rules, such as the power rule, product rule, quotient rule, and chain rule.

Power Rule – A straightforward rule used for differentiating polynomial functions.
Product Rule – Used for differentiating the product of two functions.
Quotient Rule – Helps differentiate the division of two functions.
Chain Rule – Necessary for differentiating composite functions.

Applications of Derivatives

Derivatives have a wide range of practical applications that make them invaluable in both theoretical and applied mathematics. Here are some common uses of derivatives:

Optimization – Derivatives help identify local maxima and minima of functions, which is essential for solving optimization problems in business, engineering, and economics.
Motion Analysis – In physics, derivatives describe the velocity and acceleration of objects, providing insight into their motion over time.
Curve Sketching – Derivatives allow us to understand the shape and behavior of a function’s graph by identifying critical points, inflection points, and intervals of increasing or decreasing values.
Rates of Change – Derivatives are used to calculate rates of change in various fields, such as biology for growth rates or economics for marginal costs.

Mastering derivatives not only enhances your mathematical toolkit but also enables you to tackle real-world problems with confidence. Regular practice will help you apply these concepts effectively across a variety of contexts.

Strategies for Tackling Word Problems

Word problems can often appear complex and intimidating, but breaking them down into smaller, more manageable parts makes them much easier to approach. The key is to translate the given information into a mathematical model that can be solved step by step. By following a systematic strategy, you can efficiently navigate through word problems and find the solution with greater confidence.

Step-by-Step Approach

The first step in solving any word problem is to carefully read the question and identify what is being asked. This helps to focus on the key information and discard irrelevant details. Once you understand the problem, proceed with the following steps:

Identify Known and Unknown Variables – Highlight or underline the given values and the quantities you need to find. Make note of any relationships between variables.
Translate Words into Mathematical Expressions – Convert the written descriptions into algebraic equations. Look for phrases that indicate specific operations (e.g., “total” for addition, “difference” for subtraction).
Choose the Right Formula – Depending on the problem, apply relevant formulas or theorems. This could be from geometry, trigonometry, or rates of change, for example.
Set Up and Solve the Equation – Once the equation is established, solve for the unknown variable. Be systematic and double-check each step to ensure accuracy.
Interpret the Result – Finally, make sure your solution answers the question posed by the problem. Check whether the result makes sense in the context of the problem.

Common Pitfalls and Tips for Success

While following the above steps can help you solve most word problems, there are some common mistakes to avoid. Being aware of these pitfalls can save time and prevent errors:

Misinterpreting the Question – Carefully re-read the problem to ensure you understand what is being asked. Sometimes the wording can be tricky.
Ignoring Units of Measurement – Always keep track of the units you’re working with (e.g., meters, seconds) and make sure your final answer is expressed in the correct units.
Overcomplicating the Problem – Word problems may seem complicated, but often the solution involves simple mathematical reasoning. Avoid overthinking the problem.
Not Checking the Answer – After solving the problem, take a moment to verify that the solution makes sense and fits the context of the problem.

By following these strategies, you can tackle word problems more effectively and avoid common mistakes. Practice is key, so keep working through different types of word problems to build confidence and improve problem-solving skills.

Using Graphing Calculators Efficiently

Graphing calculators are powerful tools that can significantly simplify complex mathematical problems, making it easier to visualize and solve equations, plot functions, and analyze data. However, to maximize their potential, it is important to understand how to use them effectively. By mastering the basic functions and learning advanced techniques, you can greatly improve your problem-solving efficiency.

Getting Started with the Basics

Before diving into more advanced features, it’s essential to get comfortable with the core functionalities of the graphing calculator. These are the building blocks that will support more complex calculations.

Entering Functions – Understand how to input mathematical functions, such as polynomials, trigonometric functions, and rational expressions, into the calculator.
Graphing and Viewing – Learn how to graph functions and adjust the window settings to zoom in or out for a better view of the curve.
Using Table of Values – Use the table feature to generate a list of values for a given function, helping to identify key points, trends, and behaviors of the function.

Advanced Features for Problem Solving

Once you’re comfortable with the basics, explore the more advanced features that can help solve more complex problems. These tools allow for deeper analysis and greater accuracy in calculations.

Finding Intersections – Use the calculator to find the points where two functions intersect. This is particularly helpful for solving systems of equations graphically.
Derivative and Integral Calculations – Many graphing calculators can compute derivatives and integrals. These features can be useful for evaluating rates of change or solving area problems.
Solving Equations – Learn how to use the equation solver to find roots or solutions for specific equations, helping to quickly determine where a function equals zero.
Analyzing Behavior – Use the graphing calculator to analyze function behavior such as increasing or decreasing intervals, concavity, and asymptotes.

Maximizing Efficiency and Avoiding Mistakes

To avoid errors and increase efficiency while using a graphing calculator, keep the following tips in mind:

Double-Check Settings – Always check the mode (radian or degree) and ensure the window settings are appropriate for the problem.
Practice Graphing Techniques – Regularly practice inputting and graphing functions to become more comfortable with the interface and reduce time spent on setup.
Use the Calculator’s Manual – Familiarize yourself with the calculator’s manual to discover lesser-known features and shortcuts that can streamline your work.
Avoid Over-Reliance – While graphing calculators are useful, always ensure you understand the underlying mathematical concepts. Use the calculator as a tool, not a crutch.

By using a graphing calculator efficiently, you can save time, reduce errors, and deepen your understanding of complex concepts. Practice is key, so experiment with different functions and techniques to become proficient in using this invaluable tool.

Important Theorems You Must Know

Mathematical theorems play a vital role in solving a wide variety of problems, especially in advanced topics. Understanding and applying these key theorems will not only help you solve problems faster but also deepen your grasp of underlying principles. Below are the fundamental theorems that you should thoroughly understand and be able to apply when tackling challenges in this field.

Key Theorems to Master

Here are several essential theorems that are frequently encountered in problem-solving and analysis:

Fundamental Theorem of Algebra – This theorem guarantees that every non-constant polynomial equation has at least one complex root. It’s a foundational result for solving polynomial equations.
Mean Value Theorem – It states that for any continuous function over an interval, there exists at least one point where the instantaneous rate of change (slope) equals the average rate of change over the interval. This theorem is critical for understanding the behavior of functions.
Intermediate Value Theorem – If a continuous function takes two values at the ends of an interval, it must take any value between those two values at some point within the interval. This is essential for proving the existence of solutions to equations.
Fundamental Theorem of Integration – This theorem connects the concepts of differentiation and integration, stating that the integral of a function can be evaluated using its antiderivative. It is a cornerstone of integral calculus.
Power Rule for Derivatives – This rule provides a straightforward method to differentiate polynomial functions, stating that the derivative of (x^n) is (nx^{n-1}), where n is a constant.

Theorems for Problem-Solving Techniques

In addition to the basic theorems, there are some that provide specific techniques for solving complex problems:

Rolle’s Theorem – A specific case of the Mean Value Theorem, it states that if a function is continuous and differentiable on a closed interval, and if the function has equal values at the endpoints of the interval, then at least one point exists where the derivative is zero.
Limit Laws – A collection of rules for evaluating the limits of functions, including the Sum Rule, Product Rule, and Quotient Rule, which simplify the process of calculating limits of more complex expressions.
Chain Rule – This rule allows you to differentiate composite functions, stating that the derivative of the composition of two functions is the derivative of the outer function multiplied by the derivative of the inner function.
Integration by Parts – A technique based on the product rule of differentiation, used to integrate the product of two functions. It is essential for solving integrals involving products of functions that do not easily simplify otherwise.
Trapezoidal Rule – A numerical method for approximating the value of a definite integral by dividing the area under a curve into trapezoids and summing their areas. This theorem is particularly useful when analytical methods are too complicated.

By mastering these theorems, you’ll be equipped with powerful tools to tackle even the most challenging problems. Understanding how and when to apply them is key to improving problem-solving skills and achieving a deeper understanding of the subject matter.

How to Handle Multiple Choice Questions

Multiple choice questions can be a challenging yet manageable aspect of any assessment. With the right approach, you can quickly eliminate incorrect options and confidently choose the correct answer. Developing strategies for these types of questions not only improves your speed but also boosts your accuracy during the test. Below are some effective techniques for tackling multiple choice questions.

1. Read the Question Carefully

Before looking at the options, ensure you understand what the question is asking. Often, multiple choice questions include extraneous information designed to confuse. Focus on what is being asked and identify any key terms or concepts.

2. Eliminate Clearly Incorrect Answers

Start by ruling out the answers that are obviously wrong. This will help narrow down your choices, making it easier to focus on the more plausible options. If you’re unsure, mark the question and return to it later.

3. Use Your Knowledge to Narrow Down Choices

If you’re unsure about the correct answer, use your knowledge of key concepts to eliminate some of the options. Often, multiple choice questions have at least one or two answers that don’t align with what you’ve learned, so eliminating them can increase your chances of selecting the correct one.

4. Watch for Qualifiers

Pay attention to words like “always,” “never,” “sometimes,” or “most” in the answer choices. These qualifiers can help you determine which answer is the most appropriate. For example, an answer that uses “always” might be a red flag if you know that exceptions exist to that statement.

5. Avoid Second-Guessing

Once you’ve made a decision, stick with it unless you’re absolutely certain you made a mistake. Overthinking can lead to unnecessary changes, and you may end up selecting an answer that’s less accurate than your original choice.

6. Time Management

Multiple choice sections often have a time limit, so it’s essential to manage your time efficiently. Don’t spend too long on any one question. If you’re stuck, move on and return to it later if time permits.

7. Double-Check Your Work

If you have time left, go back and review your answers. Sometimes, revisiting a question with a fresh perspective can help you spot errors or identify a better choice.

By applying these strategies, you’ll be able to approach multiple choice questions with more confidence and improve your chances of success. Remember, practice is key–regularly testing yourself with similar questions will help you develop a strong approach and sharpen your decision-making skills.

Preparing for Free Response Questions

Free response questions provide an opportunity to demonstrate your deep understanding of the subject by solving problems step by step. These questions require you to clearly articulate your thought process, justify your reasoning, and present complete solutions. Unlike multiple choice questions, they challenge you to apply your knowledge in a more comprehensive way. To succeed in these sections, preparation is essential. Below are key strategies to help you perform well in this type of assessment.

1. Practice Problem-Solving Techniques

Consistent practice with various problems is one of the most effective ways to prepare for free response questions. Work through problems from past assessments, as well as new ones that cover a broad range of topics. By practicing, you not only reinforce your understanding but also become familiar with the types of questions that may be asked. This will help you develop strategies for approaching different problem types.

2. Show All Your Work

When responding to free response questions, it’s crucial to show every step of your solution. This ensures that your logic is clear and allows the grader to follow your reasoning. Even if you make a mistake, partial credit may be awarded for the steps you completed correctly. Be sure to write down all calculations, diagrams, and explanations necessary to complete your answer.

3. Understand the Question Requirements

Before starting to solve the problem, carefully read the question and identify exactly what is being asked. Free response questions often contain multiple parts, so be sure to address each part of the question thoroughly. If the question involves multiple concepts or steps, break it down and tackle each one individually to ensure a complete answer.

4. Practice Time Management

Time management is crucial when dealing with free response sections. Each question typically requires several steps to solve, and the clock can run out quickly. Allocate your time wisely for each question and avoid spending too much time on any one problem. If you’re stuck, move on to the next part or question and return later if you have time.

5. Focus on Clear Explanations

In free response questions, clarity of explanation is just as important as the correctness of your solution. Take time to write clear, concise, and organized responses. Use proper mathematical notation and explain your reasoning in simple terms, especially when justifying steps or deriving formulas. This ensures that the grader can easily follow your logic and may award you more points for the clarity of your explanation.

6. Review Key Concepts and Formulas

Ensure you are familiar with the key formulas and concepts relevant to the problems you are likely to encounter. Review important topics, such as differentiation, integration, and optimization, as these are commonly featured in free response questions. Having a solid grasp of the core concepts will allow you to respond more effectively to complex problems.

7. Stay Calm and Confident

Free response questions can sometimes feel intimidating, but staying calm and confident can make a huge difference in your performance. If you encounter a difficult question, don’t panic. Take a deep breath, recall your practice, and apply the strategies you’ve learned. Confidence will help you think clearly and solve problems more effectively.

By following these strategies, you can enhance your ability to handle free response questions with accuracy and confidence. Consistent practice, clear explanations, and effective time management are key to mastering this part of the assessment and achieving success.

Reviewing Past Exam Papers

One of the most effective ways to prepare for any type of assessment is by reviewing past papers. By analyzing previous questions, you can gain valuable insight into the format, structure, and difficulty level of the tasks you might encounter. This process not only helps you identify patterns in the types of problems asked, but it also provides an opportunity to practice under timed conditions. Below are key benefits and strategies for reviewing past papers efficiently.

1. Understand the Question Patterns

Past assessments often follow a similar structure year after year. By carefully reviewing previous tests, you can recognize recurring themes and question types. This helps you anticipate what to focus on during your preparation and ensures that you are ready for common problem types.

2. Identify Weak Areas

While practicing with past papers, it’s important to note any questions or concepts that consistently challenge you. This will help you identify weak areas in your understanding, allowing you to direct more time and energy toward strengthening those topics before the actual assessment.

3. Practice Time Management

One of the biggest challenges in timed assessments is managing the limited time available. When reviewing past papers, simulate exam conditions by timing yourself as you work through the problems. This will help you become accustomed to the time pressure and develop strategies for managing your time effectively during the real assessment.

4. Review Solutions and Learn From Mistakes

After completing each past paper, take the time to go over the solutions, even for the questions you answered correctly. Understanding the full reasoning behind each step, especially for the problems you found difficult, is crucial for reinforcing your knowledge. By reviewing mistakes and learning from them, you can avoid repeating the same errors in future tasks.

5. Get Familiar with Marking Schemes

In many assessments, partial credit is awarded for showing work or taking a correct approach, even if the final answer is incorrect. Reviewing past papers often includes looking at marking schemes or sample solutions. This helps you understand what graders look for in a well-completed answer, so you can ensure your responses are structured in a way that maximizes points.

Year	Key Topics	Question Types
2023	Optimization, Integration, Limits	Multiple choice, Word problems, Theoretical questions
2022	Derivatives, Series, Graph Analysis	Free response, Multi-step calculations, Short answer
2021	Applications of Derivatives, Rate of Change, Continuity	Long answer, Problem-solving scenarios, Graph interpretation

By regularly reviewing past papers, you become more familiar with the types of tasks you may face, helping you to manage both your time and stress levels more effectively. This method of preparation is not just about memorizing solutions but about refining your problem-solving skills and understanding the reasoning behind each solution. Through consistent practice, you can improve your performance and approach future assessments with greater confidence.

How to Stay Calm During the Test

Remaining composed during any assessment is key to performing at your best. The pressure of answering questions under time constraints can cause stress, but learning how to manage anxiety is essential for success. In this section, we’ll discuss effective strategies for staying calm and focused throughout the duration of the test.

1. Practice Deep Breathing Techniques

When nerves start to take over, deep breathing exercises can help you regain control. By taking slow, deliberate breaths, you can reduce the physical symptoms of anxiety, such as a racing heart or shallow breathing. This technique calms the nervous system and refocuses your mind, allowing you to approach each question with a clearer head.

2. Break the Test into Manageable Segments

Rather than focusing on the entire test at once, break it down into smaller sections. Tackling one problem at a time can reduce feelings of overwhelm and keep you from panicking. Once you complete a section, take a deep breath, reset, and move on to the next one. This approach helps maintain your focus and pace, preventing unnecessary stress from building up.

Additionally, consider utilizing the following tips to improve mental resilience:

Tip	Benefit
Start with Easy Questions	Build confidence and momentum by tackling simpler questions first.
Don’t Dwell on Mistakes	Moving past errors quickly ensures that they don’t affect the rest of your performance.
Visualize Success	Mentally rehearsing a successful test experience can boost confidence and calm anxiety.
Stay Positive	A positive mindset helps you stay motivated, even when the test seems challenging.

By employing these strategies, you can keep your mind clear and focused, even when the pressure builds. Practicing mindfulness techniques, such as deep breathing, and breaking the test into smaller sections are key ways to stay calm and perform well. Remember, confidence in your preparation and ability to handle the task will lead to greater success in any situation.

Post-Test Reflection and Improvement

Once the assessment is over, the process of growth does not end. Reflecting on your performance allows you to identify strengths and areas for improvement. By evaluating your approach and understanding where mistakes occurred, you can fine-tune your study habits and strategies for future success. This section provides insights into how you can effectively reflect on your performance and use the experience to enhance your skills moving forward.

1. Review Your Mistakes

Analyzing incorrect answers is crucial in the learning process. Rather than simply acknowledging where you went wrong, take the time to fully understand why the answer was incorrect. Did you misinterpret the question, make a calculation error, or struggle with a specific concept? By understanding the root cause, you can take steps to avoid repeating similar mistakes in the future.

2. Celebrate What Went Well

While it’s important to learn from your mistakes, it’s equally important to recognize what you did well. Take note of the questions or sections that you handled with confidence and precision. Understanding your strengths helps reinforce positive habits and boosts your motivation for continued improvement.

The following table outlines a few strategies for reflecting on your performance and fostering improvement:

Action	Benefit
Review Incorrect Questions	Helps identify weak areas and clarify misunderstandings.
Set Goals for Improvement	Provides direction and focus for future study sessions.
Practice with Similar Problems	Reinforces understanding and improves problem-solving skills.
Seek Feedback from Others	Gain new perspectives and insights on how to improve your approach.

Post-assessment reflection is an essential part of the learning cycle. By identifying areas for improvement, setting goals, and reinforcing what worked well, you can continually build upon your knowledge and skills. This reflective process helps transform challenges into opportunities for growth, ensuring you’re better prepared for future assessments and learning experiences.

Mastering the Calculus AB Final Exam

Ultimate Guide to Advanced Mathematics Assessment

Understanding the Assessment Structure

Key Concepts to Focus On

Effective Study Techniques for Success