Cumulative Exam Edgenuity Precalculus Answers Guide

Preparing for an important academic assessment can be a challenging yet rewarding experience. The process involves reviewing essential topics, practicing problem-solving techniques, and gaining a deep understanding of the core concepts. With the right approach, students can approach their assessments with confidence and clarity.

To succeed in these evaluations, it’s crucial to focus on critical areas that require attention and improvement. From mathematical operations to complex theoretical knowledge, mastering these topics will help ensure success. Effective preparation strategies include working through practice problems, utilizing helpful resources, and ensuring complete comprehension of the material at hand.

Achieving mastery in this field demands consistency and dedication. Emphasizing both theory and application will not only improve test performance but also deepen your overall understanding. Stay organized, pace yourself, and approach your studies methodically to achieve the best possible outcomes.

Understanding the Cumulative Assessment Structure

Preparing for a comprehensive assessment requires a clear understanding of its overall structure. These types of evaluations are designed to test a wide range of skills and knowledge accumulated over the course of the course. The key to success lies in recognizing the different sections and how they contribute to your final performance.

Types of Questions

The assessment consists of various question types that test both theoretical and practical understanding. Here are the most common forms:

Multiple Choice: Questions that provide several answer choices, with only one correct option.
Open-Ended Problems: These require you to explain your reasoning and present detailed solutions.
Short Answer: Brief responses to specific questions or concepts.
Problem-Solving Exercises: Challenges that test your ability to apply knowledge in real-world contexts.

Key Sections of the Test

The assessment is divided into distinct sections, each focusing on a different set of skills. Here’s a breakdown:

Theory Section: Focuses on conceptual knowledge and understanding of fundamental principles.
Application Section: Tests how well you can apply learned concepts to solve problems.
Critical Thinking Section: Challenges you to think analytically and draw conclusions based on provided data.

Each section is designed to evaluate your mastery of different aspects of the subject. A well-rounded preparation plan should target all areas to ensure a comprehensive understanding.

What You Need to Know About Edgenuity

Edgenuity is an online platform that offers personalized learning experiences for students across various subjects. It provides a combination of video lessons, interactive activities, and assessments designed to help learners grasp key concepts and improve their skills. The platform’s primary goal is to offer flexible, self-paced learning that supports students in mastering the material at their own speed.

One of the main features of this platform is its adaptive learning technology, which adjusts the difficulty of tasks based on student performance. This ensures that learners are consistently challenged while also receiving the support they need to succeed. With a variety of multimedia resources, including lessons from expert instructors and interactive exercises, the platform helps make complex topics more accessible and engaging.

Tracking Progress is another significant aspect of the platform. Students are able to monitor their progress through detailed reports and feedback, allowing them to identify areas where they may need additional practice. This helps create a clear path for improvement and encourages continuous learning.

Key Concepts Covered in Precalculus

In any advanced mathematics course, certain foundational principles are essential to understanding more complex ideas. These core concepts build the framework for further study in fields like calculus, algebra, and trigonometry. Mastering these topics ensures a solid base upon which more sophisticated methods can be learned and applied.

Core Topics in the Subject

The subject explores various mathematical ideas that form the foundation for future studies. Here are some of the key areas covered:

Functions and Their Properties: Understanding different types of functions, their graphs, and their transformations.
Exponential and Logarithmic Relationships: Exploring the relationship between exponential growth and its inverse function, logarithms.
Polynomial and Rational Functions: Investigating the behavior of complex equations and their graphs.
Systems of Equations: Learning to solve multiple equations simultaneously, using methods such as substitution and elimination.
Sequences and Series: Studying patterns of numbers and their sums, including arithmetic and geometric progressions.

Important Skills and Techniques

To excel in this field, students need to develop specific skills. These include:

Graphing and Interpreting Functions: Ability to plot and interpret the behavior of various functions.
Solving Equations: Proficiency in solving both linear and non-linear equations through various methods.
Trigonometric Applications: Using trigonometric identities and solving real-world problems involving angles and distances.
Manipulating Algebraic Expressions: Simplifying complex algebraic expressions and understanding their properties.

These topics provide the essential knowledge and problem-solving strategies needed for more advanced mathematical courses and real-life applications.

Preparing for the Final Assessment

Successfully preparing for a comprehensive review of the material requires both strategic planning and disciplined practice. The key to performing well lies in understanding the scope of the content, mastering core concepts, and refining problem-solving techniques. With the right approach, you can tackle the most challenging topics with confidence and clarity.

The preparation process should focus on revisiting the most important areas covered throughout the course. This includes strengthening your understanding of key topics, practicing with sample problems, and ensuring that you can apply your knowledge effectively under timed conditions. Prioritizing the most difficult areas and dedicating extra time to them will help you feel more prepared when the time comes.

It’s also essential to review any past assignments and quizzes, as these often provide insight into the types of questions that may appear. Regular practice is vital, as repetition helps reinforce concepts and build familiarity with the testing format. Additionally, reaching out to peers or instructors for clarification on tough topics can be incredibly helpful in solidifying your understanding.

Common Mistakes to Avoid

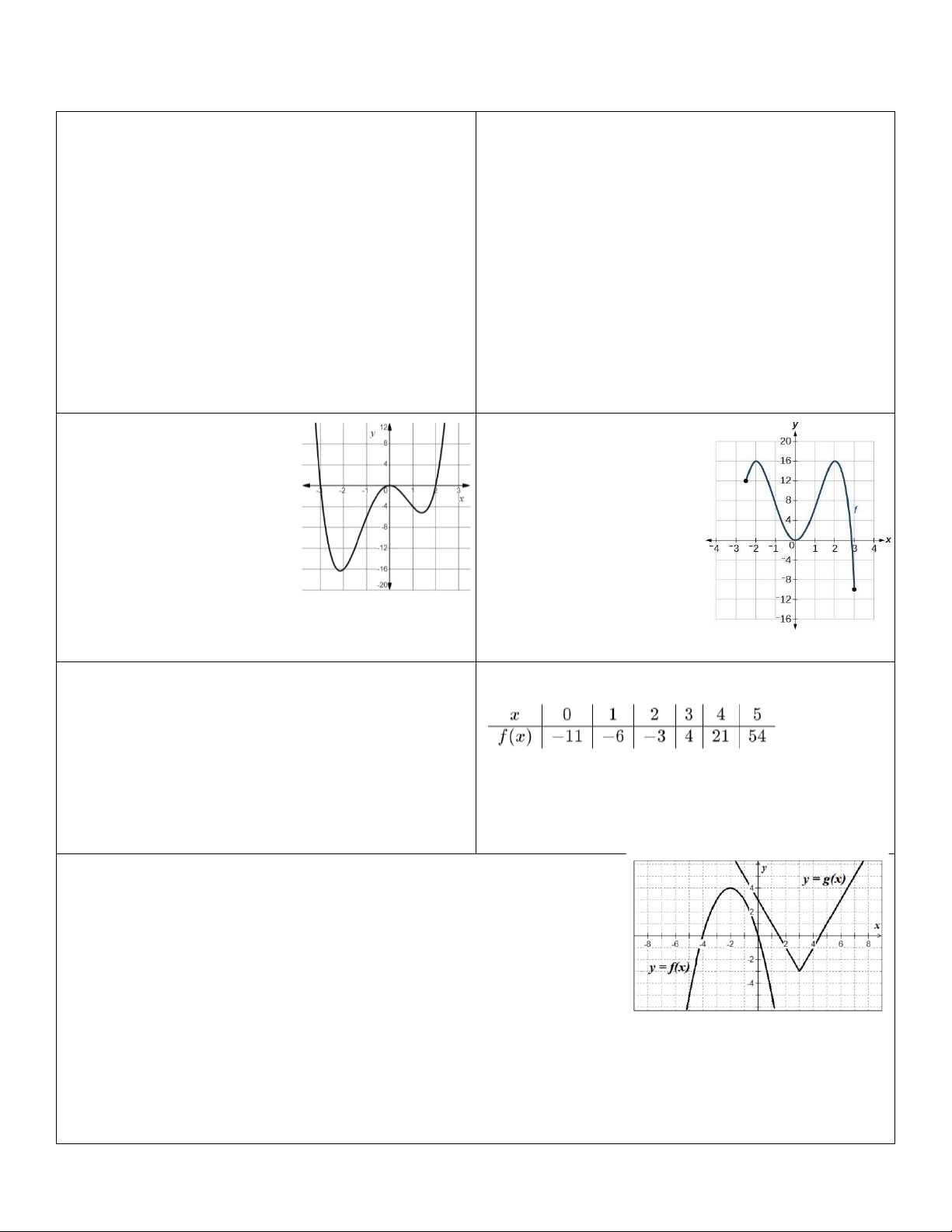
When preparing for a major assessment, it’s important to be aware of common pitfalls that can hinder your performance. Identifying and avoiding these mistakes can help ensure a smoother and more successful testing experience. Failing to address these issues may lead to unnecessary errors or missed opportunities to showcase your understanding.

Typical Errors to Watch Out For

Here are some of the most frequent mistakes students make during their preparation:

Rushing Through Questions: Trying to answer too quickly without fully understanding the problem can lead to simple mistakes. Always take your time to read each question carefully.
Ignoring Key Concepts: Skipping over important principles or assuming you understand them can leave gaps in your knowledge. Review the core concepts regularly to reinforce your understanding.
Not Practicing Enough: Relying solely on theoretical study and avoiding hands-on problem-solving can limit your ability to apply what you’ve learned under test conditions. Consistent practice is crucial.
Misunderstanding Instructions: Sometimes, misreading the directions or question requirements can lead to the wrong approach. Always clarify what is being asked before proceeding with your answer.
Overlooking Time Management: Failing to pace yourself during the assessment may result in running out of time. Practice under timed conditions to improve your speed and efficiency.

How to Avoid These Mistakes

To minimize these errors, implement the following strategies in your preparation:

Practice Regularly: Work through sample problems consistently to familiarize yourself with different question types and improve your problem-solving skills.
Stay Organized: Keep track of your study schedule and focus on weak areas to ensure well-rounded preparation.
Ask for Help: If you encounter difficult concepts, don’t hesitate to seek clarification from teachers or peers to ensure full comprehension.
Review Past Work: Go over any previous assignments, quizzes, or tests to identify areas where you made mistakes and learn from them.

By being mindful of these common pitfalls, you can improve your overall performance and approach the assessment with confidence.

How to Review Effectively

Effective review is a crucial part of preparing for any comprehensive assessment. The key is to focus on reinforcing knowledge, identifying gaps in understanding, and ensuring the material is deeply ingrained. Simply rereading notes is not enough; an active approach is necessary for true mastery of the content.

Strategies for a Productive Review

Here are some proven methods to enhance your review sessions:

Active Recall: Instead of passively reading your notes, actively quiz yourself on the material. This strengthens memory retention and helps identify areas of weakness.
Spaced Repetition: Break down your review into smaller, more manageable sessions spread over time. Revisit the material at intervals to reinforce your learning.
Teach What You Know: Explaining the concepts to someone else is an excellent way to solidify your understanding. If you can teach it, you truly understand it.
Use Practice Problems: Working through problems and scenarios forces you to apply what you’ve learned, helping you gain practical experience with the material.

Organizing Your Review Sessions

Staying organized is essential when reviewing large amounts of content. Consider the following tips:

Create a Study Schedule: Plan dedicated review sessions leading up to the assessment. Focus on high-priority topics first, and allocate more time to areas where you feel less confident.
Group Similar Topics: Break your review into themes or categories. For example, group all algebra-related concepts together, then tackle geometry, etc. This prevents jumping between unrelated topics and helps maintain focus.

By adopting these strategies and staying organized, your review sessions will become more efficient and effective, ensuring you are well-prepared for the challenge ahead.

Essential Formulas for Success

Mastering key formulas is a fundamental part of achieving success in any math-related subject. These formulas serve as the building blocks for solving problems efficiently and accurately. Having a strong grasp of essential equations and relationships not only simplifies complex tasks but also boosts confidence when tackling challenging questions.

Whether you’re solving algebraic equations, analyzing graphs, or applying geometric principles, knowing which formulas to use and when is crucial. Memorizing these formulas and understanding their application allows for quicker problem solving and fewer mistakes during assessments. Here are some of the most important formulas to commit to memory:

Quadratic Formula: Used to solve any quadratic equation in the form ax² + bx + c = 0. The solution is given by x = (-b ± √(b² – 4ac)) / 2a.
Slope Formula: To find the slope of a line given two points (x₁, y₁) and (x₂, y₂), use m = (y₂ – y₁) / (x₂ – x₁).
Pythagorean Theorem: For right-angled triangles, the relationship between the sides is a² + b² = c², where c is the hypotenuse.
Distance Formula: To find the distance between two points (x₁, y₁) and (x₂, y₂), use d = √((x₂ – x₁)² + (y₂ – y₁)²).
Area of a Circle: The area of a circle with radius r is given by A = πr².
Exponential Growth/Decay: For processes that increase or decrease exponentially, the formula is y = y₀e^(kt), where y₀ is the initial value, k is the growth or decay rate, and t is time.

These formulas form the foundation of many problems and will be useful across various areas of study. To ensure your success, review and practice these regularly until they become second nature.

Practice Problems to Boost Confidence

Consistent practice is one of the most effective ways to build confidence and solidify your understanding of complex concepts. By regularly working through a variety of practice problems, you can improve your problem-solving skills, become more familiar with different question types, and reinforce your learning. The more problems you solve, the more prepared you will be when faced with new challenges.

Key Areas to Focus On

Here are some practice areas to concentrate on for strengthening your skills and boosting confidence:

Solving Equations: Practice solving linear, quadratic, and rational equations. Ensure you can apply appropriate methods, such as factoring, completing the square, or using the quadratic formula.
Graphing Functions: Work on graphing different types of functions, including linear, exponential, and quadratic. Focus on identifying key features like intercepts, slopes, and asymptotes.
Working with Polynomials: Practice simplifying, factoring, and solving polynomial equations. Be familiar with the remainder and factor theorems.
Trigonometry: Solve problems involving right-angled triangles, unit circles, and trigonometric identities. Practice using sine, cosine, and tangent to find missing angles and sides.
Systems of Equations: Solve systems of equations using substitution, elimination, and graphical methods. Work on both linear and nonlinear systems.

Effective Practice Tips

Maximize the benefits of your practice sessions by following these strategies:

Start Simple: Begin with easier problems to build your confidence, and gradually increase the difficulty level as you progress.
Understand Mistakes: Review your errors carefully and understand why you made them. Correcting your mistakes will prevent them from happening in the future.
Set Time Limits: Practice under time constraints to simulate actual conditions and improve your ability to solve problems quickly and accurately.
Mix Up the Topics: Avoid focusing on one topic for too long. Mixing up different areas will help you retain information and avoid getting bored.

By regularly practicing these problems and using the strategies outlined, you will gain the confidence you need to succeed and tackle more advanced challenges with ease.

Strategies for Time Management

Effective time management is essential for success in any academic endeavor. It allows you to allocate the right amount of time to each task, reduces stress, and ensures that you complete everything on time. Mastering time management helps you stay organized and focused, making it easier to balance multiple tasks without feeling overwhelmed.

By implementing proven strategies, you can maximize productivity, avoid procrastination, and ensure a more efficient use of your study time. Here are some practical techniques to help you manage your time effectively:

Create a Detailed Schedule: Plan your days in advance by setting aside specific times for studying, assignments, and breaks. A well-structured schedule keeps you on track and ensures you’re not wasting time on unnecessary activities.
Prioritize Tasks: Focus on the most important and time-sensitive tasks first. Breaking larger tasks into smaller, more manageable parts can help you tackle them one step at a time.
Use the Pomodoro Technique: Break your study sessions into intervals (e.g., 25 minutes of focused work followed by a 5-minute break). This method helps maintain concentration and prevents burnout.
Avoid Multitasking: While it may seem efficient, multitasking can reduce your productivity and increase errors. Focus on one task at a time to complete it more effectively.
Set Time Limits for Each Task: Allocate a specific amount of time for each task and stick to it. This helps prevent spending too much time on a single topic and ensures that you stay on schedule.

By using these strategies, you can enhance your ability to stay focused, meet deadlines, and improve your overall productivity. Time management is a skill that, once developed, can significantly increase your efficiency and contribute to your academic success.

How to Interpret Complex Questions

Understanding complex questions is a crucial skill for academic success. These questions often contain multiple parts, require careful analysis, or present unfamiliar scenarios. Breaking them down into manageable pieces and fully grasping what is being asked can significantly improve your ability to respond correctly and efficiently.

The key to interpreting complex questions is identifying the main idea, recognizing what information is needed, and focusing on what each part of the question is asking. Once you can separate the components of a question, you can approach it with clarity and confidence.

Steps to Effectively Interpret Complex Questions

Here are some steps to help you interpret and solve complex problems more efficiently:

Step	Action	Explanation
1	Read the Question Carefully	Look for keywords and phrases that indicate what is being asked. Take your time to understand each part of the question before moving forward.
2	Identify the Key Information	Highlight the essential details, numbers, or conditions that the problem refers to. This helps avoid confusion and ensures you don’t overlook important elements.
3	Break the Problem into Parts	If the question has multiple components, tackle them one by one. Look for sub-questions or instructions within the larger problem.
4	Focus on What is Being Asked	Make sure you understand the core of the question. Ask yourself what the problem is really testing and what the expected outcome is.
5	Eliminate Irrelevant Information	Some questions contain distracting or unnecessary details. Identify what information is not needed to solve the problem and disregard it.

By following these steps, you can make sense of even the most complicated questions, ensuring that you can respond effectively and with accuracy. The more you practice this approach, the more confident and efficient you’ll become in interpreting complex challenges.

Tips for Solving Word Problems

Word problems can often seem overwhelming, as they present real-life scenarios that require careful thought and logical steps to solve. However, with the right approach, these problems can become manageable and even enjoyable to tackle. The key is to break down the problem into smaller, more understandable parts and apply a methodical approach to reach the solution.

By following a series of steps and being systematic in your thinking, you can approach word problems with confidence and accuracy. Here are some useful tips to help you solve them efficiently:

Approach to Solving Word Problems

Consider using the following steps when faced with word problems:

Step	Action	Explanation
1	Read the Problem Carefully	Take your time to read the entire problem to understand what is being asked. Look for keywords that describe relationships or quantities.
2	Identify What is Given and What is Being Asked	Highlight or note down the information provided in the problem. Clearly define what you need to find or solve.
3	Translate the Words into Mathematical Expressions	Convert the narrative into mathematical equations or expressions that represent the problem. This step helps make the problem more tangible.
4	Set Up an Equation	Based on the translated expressions, form an equation that represents the relationship between the variables involved.
5	Solve the Equation	Apply the appropriate mathematical operations to solve the equation. Double-check each step to ensure you are following the correct process.
6	Interpret the Solution	Once you have a solution, interpret it in the context of the problem. Ensure the result makes sense and addresses the question posed in the problem.

Additional Tips for Success

Practice Regularly: The more you practice, the more familiar you will become with the types of word problems you may encounter.
Draw Diagrams: For problems involving geometry or spatial relationships, sketching a diagram can help you visualize the situation and organize your thoughts.
Check Your Work: After solving the problem, review your solution and the steps you took to ensure accuracy. It’s easy to make small errors, but catching them can make a big difference.

By following these tips, you’ll be better prepared to tackle word problems with confidence and precision. With practice and patience, you’ll improve your problem-solving skills and develop a systematic approach to solving even the most complex challenges.

Using Online Resources to Study

In today’s digital age, online platforms offer a wealth of educational materials and tools that can significantly enhance your learning experience. Whether you are preparing for an assessment or strengthening your understanding of complex concepts, the internet provides access to various resources that cater to different learning styles and needs.

By using these online tools effectively, you can expand your knowledge, practice essential skills, and even engage with interactive exercises that reinforce key concepts. The flexibility of online learning allows you to study at your own pace and revisit difficult topics as needed. Below are some effective ways to leverage the internet for academic success:

Exploring Educational Websites

There are numerous websites dedicated to providing explanations, tutorials, and practice problems. These platforms often break down complicated ideas into digestible pieces, making it easier for you to grasp challenging material.

Khan Academy: A comprehensive educational site with free video lessons, quizzes, and practice exercises covering a wide range of subjects.
Coursera: Offers online courses from top universities that include lectures, assignments, and discussions to deepen your understanding.
Quizlet: A flashcard-based tool that allows students to create custom study sets or use shared ones to test their knowledge on various topics.

Interactive Learning Tools and Platforms

Interactive platforms provide a more hands-on approach to learning, allowing you to practice problems, receive instant feedback, and track your progress over time. These tools make it easier to identify areas that need improvement and focus your study efforts accordingly.

Wolfram Alpha: A powerful computational knowledge engine that helps solve mathematical problems and provides step-by-step explanations.
Desmos: An online graphing calculator that allows students to visualize equations, explore functions, and analyze data.
Edmodo: A social learning platform where students and teachers can interact, share resources, and collaborate on projects.

Incorporating these online resources into your study routine can significantly enhance your preparation and performance. By engaging with different tools, practicing consistently, and seeking additional help when needed, you can build a deeper understanding of the material and boost your academic confidence.

Understanding Graphs and Functions

Graphs and functions are fundamental concepts in mathematics that help us visualize and analyze relationships between different quantities. Understanding how to interpret and manipulate these mathematical structures is essential for solving complex problems and gaining deeper insight into various topics. Whether you’re studying algebra, calculus, or other branches of math, a solid grasp of graphs and functions will empower you to approach problems with confidence and clarity.

At their core, functions represent the relationship between input and output values, while graphs provide a visual representation of this relationship. By plotting points and connecting them on a coordinate plane, we can observe how one variable affects another. Below, we explore key concepts to help you better understand these essential tools.

Key Components of a Graph

Every graph consists of several components that define its shape and behavior. The most important elements include:

Axes: The horizontal (x-axis) and vertical (y-axis) lines that divide the plane into four quadrants.
Points: Specific locations on the graph that correspond to input-output pairs of a function.
Curves and Lines: The lines or curves formed by connecting the points, which reveal patterns in the data or function.
Intercepts: The points where the graph crosses the axes, representing important values of the function.

Types of Functions and Their Graphs

There are various types of functions, each with its own unique properties and graphical representations. Some common types include:

Linear Functions: These functions produce straight-line graphs, with a constant rate of change between the input and output values.
Quadratic Functions: These functions produce parabolic graphs, characterized by a “U” or “inverted U” shape.
Exponential Functions: These functions create graphs that increase or decrease rapidly, showing exponential growth or decay.

By recognizing these different function types and their corresponding graph shapes, you can more easily analyze the behavior of mathematical relationships and solve problems effectively. Familiarizing yourself with these basic concepts will provide a strong foundation for tackling more advanced topics in mathematics.

Key Topics in Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is a crucial subject that has broad applications in fields such as physics, engineering, architecture, and computer science. A solid understanding of key trigonometric principles can significantly enhance problem-solving skills in various mathematical contexts.

In this section, we will explore the essential concepts and functions that form the foundation of trigonometry. These topics provide the necessary tools to understand and solve real-world problems involving angles and distances.

Trigonometric Functions

The trigonometric functions are central to understanding the relationships between angles and sides in triangles. The six main functions include:

Sine (sin): The ratio of the opposite side to the hypotenuse in a right triangle.
Cosine (cos): The ratio of the adjacent side to the hypotenuse.
Tangent (tan): The ratio of the opposite side to the adjacent side.
Cosecant (csc): The reciprocal of sine, or the ratio of the hypotenuse to the opposite side.
Secant (sec): The reciprocal of cosine, or the ratio of the hypotenuse to the adjacent side.
Cotangent (cot): The reciprocal of tangent, or the ratio of the adjacent side to the opposite side.

Important Identities

Trigonometric identities are equations that hold true for all values of the variables within their domains. Some of the most important identities include:

Pythagorean Identity: sin²(θ) + cos²(θ) = 1, a fundamental identity used to simplify expressions involving trigonometric functions.
Angle Sum and Difference Identities: These identities help simplify expressions involving the sum or difference of two angles. For example, sin(A + B) = sin(A)cos(B) + cos(A)sin(B).
Double Angle Formulas: These are used to express trigonometric functions of double angles, such as sin(2θ) = 2sin(θ)cos(θ).

Mastering these fundamental concepts allows for greater flexibility in solving a wide range of problems in trigonometry. Whether dealing with angles in a triangle or analyzing periodic phenomena, these topics serve as the building blocks for more advanced study in mathematics and its applications.

Handling Difficult Problem Types

Mathematical problems can often present unexpected challenges, especially when the concepts involved are complex or unfamiliar. These problems may require a different approach or more strategic thinking to break down and solve efficiently. Understanding how to approach and manage difficult problem types is essential for developing strong problem-solving skills and achieving success in any mathematical field.

In this section, we will focus on various strategies for handling challenging questions, breaking them into manageable steps, and applying techniques that will help you stay confident and organized during problem-solving.

Identifying Common Problem Types

There are several categories of difficult problems that students often encounter. Recognizing these patterns early on can help streamline the approach. Below is a table summarizing some common problem types and suggested strategies for each:

Problem Type	Strategy
Word Problems	Carefully read the problem, underline key information, and translate it into mathematical expressions. Identify what is being asked and choose the appropriate formula or method.
Equations with Multiple Variables	Use substitution or elimination methods to reduce the complexity. Solve step by step and check each part of the solution.
Trigonometric Functions	Apply identities and use the unit circle for simplification. Work with known values and use calculators if needed for precise answers.
Graph Interpretation	Analyze the graph’s key features, such as intercepts, slopes, and asymptotes. Use known formulas to interpret the graph’s behavior.

Key Strategies for Difficult Problems

Here are several essential techniques that can make complex problems easier to manage:

Break down the problem: Divide the problem into smaller, more manageable parts. Solve each part individually before combining them into the final solution.
Use diagrams or visuals: Drawing out a problem can clarify relationships between components and offer insight into the solution process.
Check for errors: Double-check each step in your solution to ensure no mistakes were made. Mistakes in one step can compound, leading to an incorrect final result.
Seek patterns: Many problems have underlying patterns that can help you identify shortcuts or simplify the solution process.

By practicing these techniques and familiarizing yourself with common problem types, you can reduce the difficulty of complex problems and approach them with confidence. With time, you will become more adept at solving even the toughest challenges.

Improving Your Answer Accuracy

Achieving precision in problem-solving is essential, especially when dealing with complex tasks or intricate calculations. Ensuring that each step is correct and that no errors are made can significantly impact the final result. Improving your accuracy is not only about understanding the methods but also about developing habits that help minimize mistakes and increase reliability in your solutions.

In this section, we will explore strategies for refining your approach, focusing on common sources of errors and how to avoid them. By paying attention to details, organizing your work systematically, and reviewing your process, you can enhance your overall performance and minimize inaccuracies in your results.

Key Strategies for Enhancing Accuracy

Here are some effective approaches to help you improve your answer accuracy:

Work Step by Step: Break complex problems into smaller, manageable steps. This makes it easier to identify and correct errors early on in the process.
Double-Check Your Work: Always review your solution after completing it. Going over each step can help catch minor mistakes, such as sign errors or calculation missteps.
Use Estimation: Before diving into complex calculations, estimate the expected range or general size of the answer. This will help you spot any glaring errors in your final solution.
Practice Mental Math: Improve your mental calculation skills to speed up your work and reduce reliance on calculators, which can sometimes introduce errors.
Learn from Mistakes: When an error occurs, take the time to understand why it happened. Identifying patterns in mistakes can help you avoid them in the future.

Tools to Support Accurate Solutions

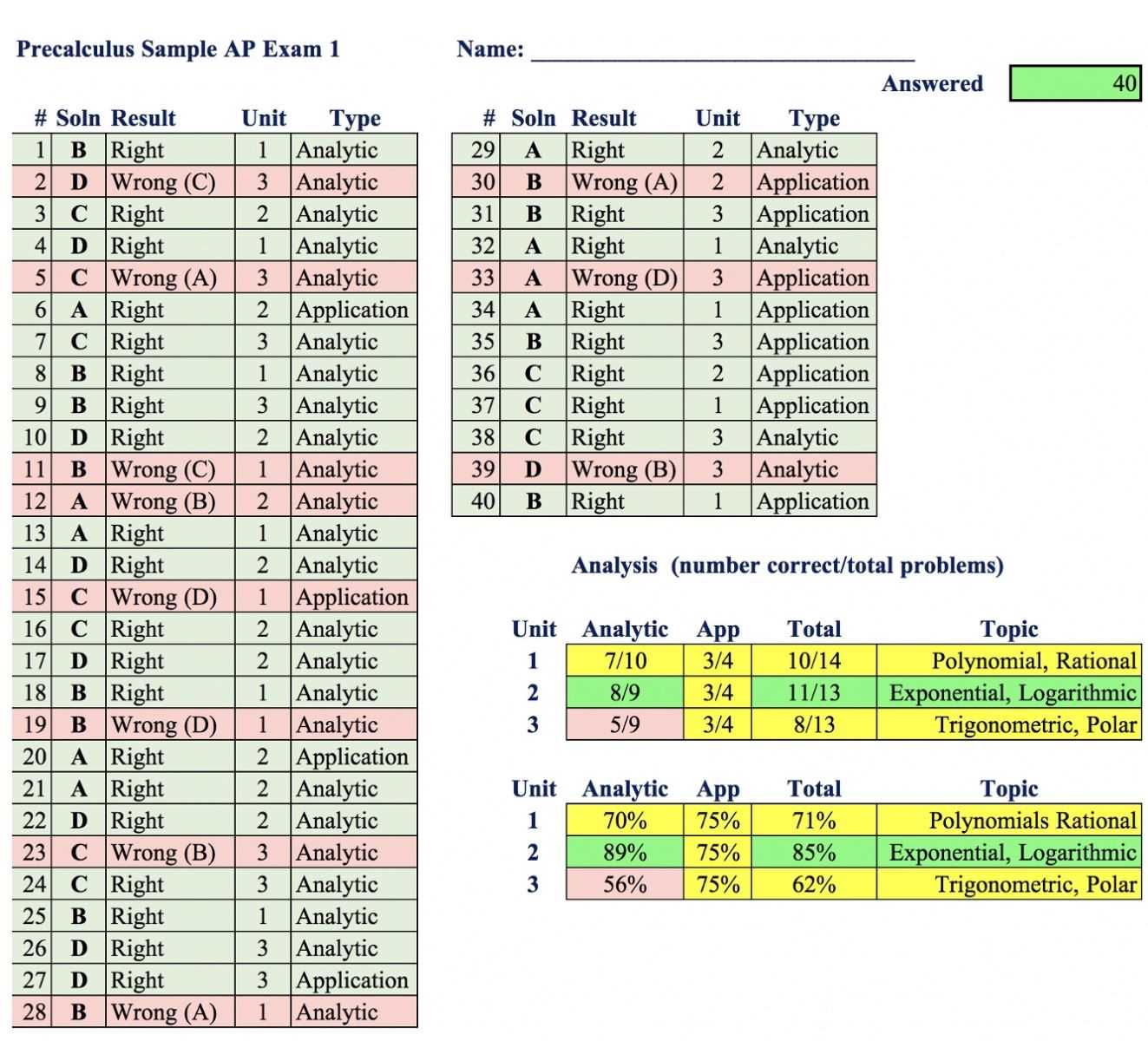
There are several tools and resources that can aid in ensuring your work is accurate:

Graphing Calculators: These can provide visual confirmation of your solutions, especially for equations involving graphs or curves.
Checklists: Create a checklist for each problem type to ensure that every step is followed correctly, from the initial setup to the final solution.
Peer Review: If possible, have someone else review your work to catch any potential errors that you might have missed.

By implementing these strategies and tools, you can significantly improve the accuracy of your solutions. Focusing on the process, rather than just the outcome, will help you develop stronger problem-solving skills and consistently produce correct results.

Staying Calm During the Exam

Staying composed in a high-pressure situation is essential for performing at your best. When faced with a challenging task, stress and anxiety can cloud your judgment and hinder your ability to think clearly. By developing strategies to stay calm and focused, you can enhance your problem-solving abilities and navigate even the most difficult scenarios with confidence.

In this section, we will discuss techniques that can help you maintain your composure, reduce stress, and improve your overall performance. By incorporating these methods, you can face difficult challenges with a clear mind and stay on track to achieve your goals.

Effective Techniques for Staying Calm

Deep Breathing: Taking deep, slow breaths can help activate your body’s relaxation response. This simple technique can reduce anxiety and restore your focus during stressful moments.
Positive Visualization: Imagine yourself successfully completing the task at hand. Visualization can help reduce negative thoughts and build confidence in your abilities.
Time Management: Avoid feeling overwhelmed by breaking the task into manageable segments. By allocating a set amount of time for each part, you can stay organized and reduce stress.
Take Short Breaks: If you feel your mind becoming overloaded, take a brief pause to reset. Even just a few seconds of stretching or deep breathing can help you regain focus.
Stay Hydrated: Dehydration can increase feelings of fatigue and anxiety. Drinking water throughout the process will keep your body and mind alert and reduce unnecessary stress.

Building Confidence and Reducing Anxiety

Confidence plays a crucial role in managing stress. When you trust in your abilities, you are less likely to be overwhelmed by challenges. Here’s how you can build your confidence and reduce anxiety:

Preparation: Adequate preparation is key to feeling ready and confident. Knowing the material inside and out can help you approach challenges with assurance.
Stay in the Present Moment: Avoid getting distracted by thoughts about future tasks. Focus on the task in front of you and take one step at a time.
Positive Affirmations: Remind yourself that you are capable and prepared. Positive self-talk can shift your mindset and boost your morale.

By using these strategies, you can effectively manage stress, maintain focus, and perform at your best under pressure. Staying calm is not just about the absence of stress–it’s about learning how to harness it in a way that supports your success.