When preparing for a challenging science test, having a reliable set of key concepts and calculations is invaluable. This guide is designed to provide you with the crucial information you need for success in any related assessment. Understanding the core principles and formulas is essential to mastering the subject and excelling in your studies.
From reaction equations to thermodynamic relationships, knowing the right tools to use during your preparation will help simplify complex problems and reinforce your understanding of important topics. This resource covers various critical aspects of the field, offering an organized approach to solving common problems.
Whether you are working through stoichiometry, solving for equilibrium constants, or dealing with complex molecular interactions, having a clear overview of the vital equations will enable you to tackle the most difficult tasks with confidence. With this reference, you can focus on applying your knowledge rather than scrambling for information during your studies.
ACS General Chemistry Exam Formula Sheet
Having a comprehensive reference for key concepts and calculations is crucial when preparing for any science-based assessment. The right set of essential equations and principles can significantly improve efficiency and accuracy when working through problems. This section highlights the most important topics and their corresponding formulas that will help guide you through complex questions and ensure a strong performance on your test.
Below is a collection of crucial relationships and expressions that every student should be familiar with:
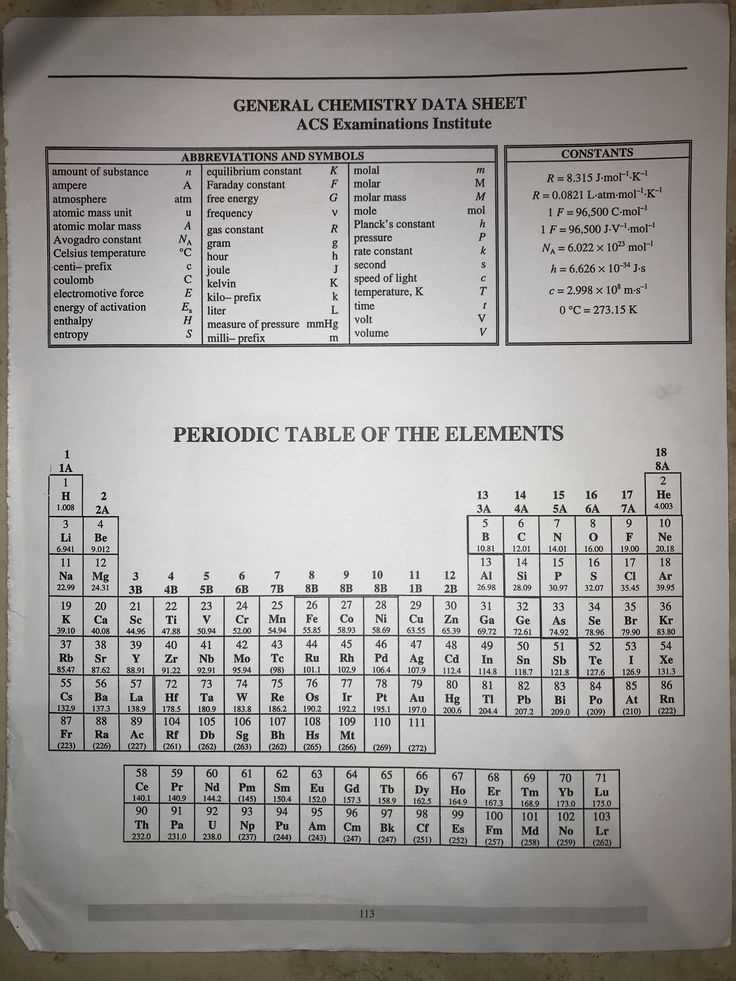
- Atomic Structure and Periodicity: Essential concepts regarding atomic numbers, electron configurations, and periodic trends.
- Thermodynamic Properties: Important equations for enthalpy, entropy, and Gibbs free energy.
- Reaction Kinetics: Key rate laws and factors affecting the speed of reactions.
- Equilibrium Principles: Expressions for calculating equilibrium constants and related quantities.
- Gas Laws: Equations describing the behavior of gases under various conditions.
- Acid-Base Concepts: Key relationships between pH, pKa, and buffer calculations.
These fundamental equations form the backbone of problem-solving in the field. Mastery of these concepts allows you to quickly navigate through more complex problems, ensuring that you can solve them correctly and efficiently. Reviewing these relationships often will help reinforce your understanding and application of the material.
In addition to mastering the equations themselves, it’s essential to understand how to apply them in different contexts. Having this knowledge readily available during preparation ensures that you’re not just memorizing equations but also developing the skills needed to interpret and solve problems under exam conditions.
Essential Formulas for General Chemistry
Understanding and applying key equations is fundamental when tackling problems in any scientific discipline. A solid grasp of essential relationships allows students to solve a wide range of problems with accuracy and confidence. This section outlines some of the most crucial equations and their practical applications across various topics.
Below is a table featuring essential equations that every student should familiarize themselves with:
| Concept | Equation | Explanation |
|---|---|---|
| Ideal Gas Law | PV = nRT | Relates pressure, volume, temperature, and amount of gas. |
| Boyle’s Law | P₁V₁ = P₂V₂ | Describes the inverse relationship between pressure and volume at constant temperature. |
| Charles’s Law | V₁/T₁ = V₂/T₂ | Shows the direct relationship between volume and temperature at constant pressure. |
| Law of Mass Action | K = [products]/[reactants] | Defines the equilibrium constant in terms of concentrations of reactants and products. |
| Hess’s Law | ΔH₁ + ΔH₂ = ΔH₃ | States that the total enthalpy change is the sum of the enthalpy changes for the steps in a reaction. |
| Arrhenius Equation | k = Ae^(-Ea/RT) | Describes the temperature dependence of reaction rates. |
| Heat Transfer | q = mcΔT | Calculates heat absorbed or released by a substance based on its mass, specific heat, and temperature change. |
These equations are key tools for solving various types of problems and understanding how different variables interact in chemical reactions. Mastery of these formulas will not only help during assessments but also deepen your overall comprehension of fundamental scientific concepts.
Key Chemical Reactions to Know
Familiarity with fundamental reactions is essential for solving a wide variety of problems in the field. Recognizing reaction types, understanding their mechanisms, and being able to predict products are skills that will serve you well in any scientific setting. This section outlines some of the most important reactions to know, as they frequently appear in assessments and practical applications.
The following table highlights key reactions and their general forms:
| Reaction Type | General Equation | Description |
|---|---|---|
| Synthesis Reaction | A + B → AB | Two or more substances combine to form a more complex product. |
| Decomposition Reaction | AB → A + B | A compound breaks down into two or more simpler substances. |
| Single Displacement Reaction | A + BC → AC + B | One element replaces another in a compound. |
| Double Displacement Reaction | AB + CD → AD + CB | Two compounds exchange ions to form new compounds. |
| Combustion Reaction | Fuel + O₂ → CO₂ + H₂O | Occurs when a substance reacts with oxygen, releasing energy. |
| Redox Reaction | Oxidation: A → A⁺ + e⁻, Reduction: B + e⁻ → B⁻ | Involves the transfer of electrons between species. |
| Neutralization Reaction | HA + BOH → H₂O + AB | An acid reacts with a base to form water and a salt. |
By mastering these reaction types and understanding their general forms, you can apply this knowledge to predict outcomes and solve problems more efficiently. These reactions are foundational, appearing across various topics, and knowing how to approach them is essential for success in your studies and beyond.
Understanding Molarity and Concentration
Accurately determining the strength of a solution is essential in many scientific applications. Concentration refers to the amount of solute dissolved in a given amount of solvent, and understanding how to calculate and express this is critical for preparing solutions and carrying out experiments. One of the most common ways to express concentration is through molarity, a measure that provides insight into how many moles of solute are present in one liter of solution.
Molarity is defined as the number of moles of solute per liter of solution. It is represented by the symbol M, and the formula used to calculate molarity is:
M = moles of solute / liters of solution
Knowing how to calculate molarity allows for precise preparation of solutions with desired concentrations, which is especially important in titrations, reactions, and other laboratory processes. To understand this concept better, let’s consider a simple example:
If 2 moles of sodium chloride (NaCl) are dissolved in 1 liter of water, the molarity of the resulting solution would be 2 M (2 moles per liter). If the same amount of solute is dissolved in 0.5 liters of solution, the molarity would be 4 M.
In addition to molarity, other ways to express concentration include molality and percent composition. However, molarity is the most widely used measurement in many fields due to its simplicity and effectiveness in a variety of chemical reactions and processes.
Important Units for Your Chemistry Exam
When working with various scientific concepts, it’s essential to understand and correctly use the units that accompany them. Whether you’re measuring pressure, volume, temperature, or energy, knowing the proper units will help you solve problems more effectively and ensure that your results are consistent and accurate. This section will focus on the most important units you need to be familiar with in order to navigate through typical questions and tasks.
Commonly Used Units in Scientific Calculations
SI units (International System of Units) form the foundation of most scientific measurements. Below are some of the key units that are frequently used in the field:
- Meter (m): The standard unit for measuring length or distance.
- Liter (L): A unit of volume, commonly used for liquids.
- Gram (g): The unit for measuring mass.
- Mole (mol): A unit that measures the amount of substance based on the number of particles, atoms, or molecules.
- Kelvin (K): The unit for temperature in absolute terms, used to avoid negative values.
- Joule (J): A unit of energy, work, or heat.
Pressure and Concentration Units
In addition to basic physical measurements, there are other specific units that are important for various reactions and processes:
- Atmosphere (atm): A common unit for measuring pressure, especially in gas laws.
- Pascal (Pa): A more precise unit for pressure, often used in thermodynamics.
- Molarity (M): A unit used to express concentration, typically in moles per liter of solution.
- Percentage (%): Used to express concentrations in terms of weight or volume.
Understanding how to properly use and convert between these units is vital to performing calculations accurately and efficiently. Familiarizing yourself with these measurements and practicing their application will greatly enhance your problem-solving abilities in the subject.
Thermodynamics Equations and Concepts
Thermodynamics is a branch of physics and physical chemistry that deals with heat, energy, and work, as well as the transformations between these forms. Understanding the fundamental laws and equations of thermodynamics is crucial for predicting how energy will flow in various systems, from chemical reactions to physical changes. This section highlights key equations and concepts that you should be familiar with when studying energy and its various forms in different contexts.
Key Thermodynamic Laws
There are four primary laws in thermodynamics, each describing a fundamental principle regarding energy conservation, entropy, and system equilibrium. The following table summarizes these laws:
| Law | Description |
|---|---|
| First Law of Thermodynamics | Energy cannot be created or destroyed, only transferred or converted from one form to another (ΔU = Q – W). |
| Second Law of Thermodynamics | The total entropy of an isolated system can never decrease over time, and energy transformations always increase entropy. |
| Third Law of Thermodynamics | As the temperature of a system approaches absolute zero, the entropy of the system approaches a constant minimum. |
| Zeroth Law of Thermodynamics | If two systems are each in thermal equilibrium with a third system, they are in thermal equilibrium with each other. |
Common Thermodynamic Equations
Thermodynamics involves several key equations that are used to calculate various properties like internal energy, enthalpy, and entropy. Below are some of the most important equations:
| Equation | Description |
|---|---|
| ΔU = Q – W | The change in internal energy of a system (ΔU) is equal to the heat added to the system (Q) minus the work done by the system (W). |
| H = U + PV | The enthalpy (H) of a system is the sum of its internal energy (U) and the product of pressure (P) and volume (V). |
| ΔH = ΔU + PΔV | The change in enthalpy (ΔH) is equal to the change in internal energy (ΔU) plus the work done due to volume change (PΔV). |
| ΔS = Qrev / T | The change in entropy (ΔS) is equal to the reversible heat transfer (Qrev) divided by the temperature (T) at which the transfer occurs. |
| ΔG = ΔH – TΔS | The change in Gibbs free energy (ΔG) is equal to the change in enthalpy (ΔH) minus the product of temperature (T) and change in entropy (ΔS). |
These equations play a fundamental role in understanding energy flow, efficiency, and spontaneity in physical and chemical processes. Mastering them will enable you to tackle complex thermodynamic problems and predict the behavior of various systems under different conditions.
Gas Laws and Their Applications

The behavior of gases is governed by a set of fundamental principles that describe the relationship between variables such as pressure, volume, temperature, and the amount of gas present. Understanding these principles allows scientists to predict how gases will behave under different conditions. These laws are not only essential in scientific studies but are also applied in real-world scenarios, such as in the design of engines, weather forecasting, and even in medical treatments like breathing therapy.
Here are some of the key gas laws and their applications:
Boyle’s Law
Boyle’s Law explains the inverse relationship between pressure and volume for a given amount of gas at a constant temperature. If the volume of a gas decreases, its pressure increases, and vice versa. This principle is widely used in understanding the behavior of gases in confined spaces, such as in the operation of syringes, scuba diving tanks, and engines.
- Mathematical Expression: P1V1 = P2V2
- Application: It is applied in breathing mechanics, where the volume of the lungs decreases during exhalation, causing an increase in pressure that expels air.
Charles’s Law

Charles’s Law states that the volume of a gas is directly proportional to its temperature, provided that the pressure and amount of gas remain constant. This law is essential for understanding the behavior of gases in various temperature conditions.
- Mathematical Expression: V1/T1 = V2/T2
- Application: It is used in hot air balloons, where heating the air causes the gas to expand, increasing the volume and allowing the balloon to rise.
Avogadro’s Law

Avogadro’s Law explains the relationship between the volume of a gas and the number of gas molecules at constant temperature and pressure. It states that the volume of gas is directly proportional to the number of molecules, assuming constant temperature and pressure.
- Mathematical Expression: V1/n1 = V2/n2
- Application: It is applied in understanding the ideal gas behavior and in stoichiometric calculations involving gases.
Ideal Gas Law
The Ideal Gas Law combines the individual gas laws into one equation, providing a comprehensive relationship between pressure, volume, temperature, and the amount of gas. It serves as a model for understanding the behavior of gases in a wide range of conditions.
- Mathematical Expression: PV = nRT
- Application: This law is used in the design of gas-powered engines and refrigerators, and in understanding the behavior of gases in various environments, such as the atmosphere.
Real-World Applications
Gas laws are essential in various industries, including:
- Medical Field: Used in calculating the proper dosage of gases like oxygen for patients and in the functioning of medical equipment like ventilators.
- Environmental Science: Helps in understanding the behavior of atmospheric gases, such as carbon dioxide, and predicting weather patterns.
- Engineering: Applied in designing engines, compressors, and refrigeration systems that rely on gas expansion and compression.
By mastering these fundamental principles, you can better understand the behavior of gases and apply this knowledge to both scientific and practical challenges in everyday life.
Equilibrium Constants and Calculations
At a certain point, many chemical reactions reach a state where the forward and reverse reactions occur at the same rate. This state, known as equilibrium, is characterized by a balance between the concentration of reactants and products. The equilibrium constant (K) quantifies this balance and provides insights into the direction in which a reaction favors. Understanding equilibrium constants is essential for calculating concentrations and predicting the behavior of chemical reactions under various conditions.
The equilibrium constant is calculated using the concentrations of the products and reactants at equilibrium. It is a crucial factor in determining how changes in concentration, pressure, or temperature can affect the system’s equilibrium position. Below is an explanation of how equilibrium constants are expressed for different types of reactions.
Expression of Equilibrium Constants

The general form of an equilibrium constant expression is as follows:
| Reaction | Equilibrium Expression (K) |
|---|---|
| A + B ⇌ C + D | K = [C][D] / [A][B] |
| 2A + 3B ⇌ 4C | K = [C]^4 / [A]^2[B]^3 |
| 3A ⇌ B + C | K = [B][C] / [A]^3 |
In these expressions, square brackets denote the concentration of the substances, and the exponents represent their coefficients in the balanced equation. The equilibrium constant (K) depends on the specific reaction and temperature but is independent of the initial concentrations.
Calculations Involving Equilibrium Constants
When performing calculations with equilibrium constants, the concentrations of the substances at equilibrium are required. In many cases, the ICE (Initial, Change, Equilibrium) table is used to help solve for these concentrations. Here’s how you can approach equilibrium problems:
- Step 1: Write the balanced chemical equation for the reaction.
- Step 2: Set up an ICE table to track the initial concentrations, the changes that occur as the reaction progresses, and the equilibrium concentrations.
- Step 3: Substitute the equilibrium concentrations into the equilibrium constant expression and solve for the unknowns.
Here is an example of how to use the equilibrium constant to calculate the concentration of a product in a reaction:
| Reaction | Equilibrium Expression (K) |
|---|---|
| CO(g) + 2H2(g) ⇌ CH3OH(g) | K = [CH3OH] / [CO][H2]^2 |
Assume that at equilibrium, the concentrations are known for CO and H2, and you are asked to find the concentration of CH3OH. You would use the ICE table to calculate the missing concentration.
Impact of Changes on Equilibrium

The principle of Le Chatelier helps predict how changes in concentration, temperature, and pressure affect the equilibrium position. If the concentration of a reactant is increased, the equilibrium will shift to the right, producing more products. Conversely, if the concentration of a product is increased, the equilibrium will shift to the left, favoring the reactants.
Understanding equilibrium constants and how to perform calculations involving them is vital for predicting reaction outcomes and controlling processes in both laboratory and industrial settings.
Acid-Base Reactions and pH Formulas
Acid-base reactions are a fundamental aspect of chemical processes that involve the transfer of protons (H⁺) between substances. These reactions are crucial in various biological, environmental, and industrial processes. The strength of acids and bases is often measured by their ability to dissociate in water, and the concentration of hydrogen ions (H⁺) determines the acidity or alkalinity of a solution. Understanding how to calculate pH and perform related calculations is essential for interpreting these reactions and controlling their outcomes in practical applications.
The pH scale is a logarithmic scale used to express the acidity or basicity of a solution. It is calculated based on the concentration of hydrogen ions present in the solution. A solution with a higher concentration of hydrogen ions is acidic, while one with a lower concentration is basic. The neutral point, corresponding to a pH of 7, is where the concentration of H⁺ and OH⁻ ions are equal.
pH Calculation

The pH of a solution is calculated using the following equation:
pH = -log[H⁺]
Where [H⁺] represents the concentration of hydrogen ions in moles per liter (mol/L). This formula helps determine the acidity of a solution. For example, if the concentration of hydrogen ions is 1 × 10⁻³ mol/L, the pH would be:
pH = -log(1 × 10⁻³) = 3
Thus, the solution would be acidic, with a pH of 3.
pOH and pH Relationship
The pOH is a measure of the concentration of hydroxide ions (OH⁻) in a solution. It is related to the pH by the following equation:
pH + pOH = 14
Since pH and pOH are inversely related, knowing one can help you calculate the other. If the pH of a solution is 4, you can calculate the pOH as follows:
pOH = 14 – pH = 14 – 4 = 10
Acid-Base Neutralization
In acid-base reactions, an acid reacts with a base to form water and a salt. The general reaction is as follows:
HA + BOH → H₂O + BA
Where HA is an acid and BOH is a base. In this neutralization reaction, hydrogen ions from the acid combine with hydroxide ions from the base to form water. This type of reaction is essential in various processes, such as titration, where the amount of acid or base required to neutralize a solution is determined.
Buffer Solutions
Buffer solutions are designed to resist changes in pH when small amounts of acid or base are added. These solutions contain a weak acid and its conjugate base or a weak base and its conjugate acid. Buffers are critical in maintaining stable pH levels in biological systems, such as blood, which has a natural pH of around 7.4. The ability of buffers to maintain pH is explained by the following equation:
pH = pKa + log([A⁻]/[HA])
Where pKa is the acid dissociation constant, and [A⁻] and [HA] are the concentrations of the conjugate base and acid, respectively.
Understanding acid-base reactions and how to calculate pH is essential for grasping many chemical processes, from simple laboratory experiments to complex biological systems and environmental chemistry.
Redox Reactions and Electrochemistry

Redox reactions involve the transfer of electrons between two substances, resulting in changes to their oxidation states. These reactions play a key role in numerous processes, including energy production, corrosion, and biological functions. In redox processes, one substance loses electrons (oxidation), while another gains them (reduction). Electrochemistry explores the relationship between chemical reactions and electrical energy, focusing on how redox reactions can be used to generate electricity or how electrical energy can drive chemical changes.
In any redox reaction, it is crucial to identify the substances being oxidized and reduced, as well as to balance the electrons involved in the process. The movement of electrons between the reacting species can be harnessed to do useful work, such as in batteries or fuel cells, where chemical energy is converted into electrical energy.
Oxidation States and Half-Reactions
To understand redox reactions, one must first determine the oxidation states of the elements involved. The oxidation state is a measure of the degree of oxidation of an atom in a compound. In a redox reaction, the substance that loses electrons is oxidized (its oxidation state increases), while the substance that gains electrons is reduced (its oxidation state decreases).
Redox reactions can be split into two half-reactions: one for oxidation and one for reduction. The oxidation half-reaction shows the substance losing electrons, while the reduction half-reaction shows the substance gaining electrons. The overall reaction is obtained by combining the two half-reactions and balancing the number of electrons transferred.
Electrochemical Cells

Electrochemical cells are devices that convert chemical energy into electrical energy or vice versa. A common example is the galvanic cell, where spontaneous redox reactions occur, producing an electric current. In these cells, the oxidation half-reaction occurs at the anode, and the reduction half-reaction occurs at the cathode. The flow of electrons from the anode to the cathode through an external circuit generates an electric current.
In an electrolytic cell, the process is reversed: electrical energy is applied to drive a non-spontaneous redox reaction. This type of cell is used in electroplating and the extraction of metals from ores, where external electricity is used to cause chemical changes that would not occur naturally.
Standard Electrode Potentials
Each half-reaction has an associated standard electrode potential, which is a measure of the tendency of a species to gain or lose electrons. The more positive the electrode potential, the greater the tendency to gain electrons (reduction). Conversely, a more negative electrode potential indicates a greater tendency to lose electrons (oxidation).
The overall cell potential is the difference between the electrode potentials of the cathode and anode. This potential determines the spontaneity of the redox reaction: if the cell potential is positive, the reaction is spontaneous, and if it is negative, the reaction is non-spontaneous and requires external energy to occur.
Applications of Electrochemistry
Electrochemistry has numerous applications, from energy storage in batteries to industrial processes like electrolysis. In rechargeable batteries, such as lithium-ion batteries, redox reactions store and release energy as the battery is charged and discharged. Fuel cells, which generate electricity from the reaction of hydrogen and oxygen, are another important application, offering an environmentally friendly alternative to conventional energy sources.
Understanding the principles of redox reactions and electrochemistry is essential for developing technologies that rely on the efficient use of electrical and chemical energy. These concepts form the basis of everything from energy storage devices to corrosion prevention strategies, making them crucial in both academic and industrial settings.
Atomic Structure and Periodic Trends
Understanding the structure of atoms is essential for grasping how elements interact with each other and the fundamental principles of matter. Atoms are composed of a nucleus containing protons and neutrons, surrounded by a cloud of electrons. The arrangement and behavior of these electrons determine the chemical properties of an element and its position on the periodic table. Elements exhibit periodic trends that reflect recurring patterns in their atomic structure, such as ionization energy, atomic radius, and electronegativity.
The periodic table is organized based on the atomic number, which represents the number of protons in an atom’s nucleus. This organization reveals periodic trends that allow us to predict the chemical behavior of elements. For example, elements in the same group (vertical columns) share similar chemical properties, while elements in the same period (horizontal rows) exhibit variations in these properties due to differences in electron configuration.
Atomic Radius

The atomic radius refers to the size of an atom, typically measured as the distance from the nucleus to the outermost electron. This trend decreases across a period from left to right due to the increasing number of protons in the nucleus, which pulls electrons closer, reducing the atomic size. In contrast, atomic radius increases down a group because additional electron shells are added, making the atom larger despite the increase in nuclear charge.
Ionization Energy
Ionization energy is the amount of energy required to remove an electron from an atom in the gas phase. This energy increases across a period as the effective nuclear charge increases, holding the electrons more tightly. On the other hand, ionization energy decreases as you move down a group because electrons are farther from the nucleus and are more shielded by inner electron shells, making them easier to remove.
Electronegativity
Electronegativity is a measure of an atom’s ability to attract electrons in a chemical bond. It generally increases across a period as atoms become smaller and their effective nuclear charge increases, making them better at attracting electrons. Electronegativity decreases down a group due to the increasing distance between the nucleus and the valence electrons, reducing the nucleus’s ability to attract electrons.
Electron Affinity
Electron affinity refers to the energy change that occurs when an atom gains an electron. In general, atoms with high electronegativity tend to have higher electron affinities. This property follows trends similar to electronegativity, with a tendency for electron affinity to become more negative across periods and less negative down groups.
Applications of Periodic Trends
Periodic trends provide valuable insight into the chemical behavior of elements. For instance, understanding atomic size and ionization energy helps explain why certain elements readily form positive or negative ions. Similarly, trends in electronegativity play a key role in determining the nature of chemical bonds–whether they are ionic, covalent, or polar covalent. The knowledge of these trends is fundamental for predicting reactivity, bonding patterns, and molecular structure in various chemical reactions and compounds.
Stoichiometry and Mole Concept
Understanding the relationship between quantities of reactants and products in chemical reactions is crucial for accurate calculations in many scientific fields. Stoichiometry provides the tools needed to determine the amounts of substances consumed or produced during a reaction. This process relies heavily on the mole concept, which relates macroscopic quantities of matter to the number of particles involved in chemical processes.
The mole is a fundamental unit in science that allows chemists to count entities like atoms, molecules, or ions by weighing them. One mole of any substance contains the same number of particles–approximately 6.022 × 10²³, known as Avogadro’s number. This concept bridges the gap between the atomic scale and the macroscopic scale, enabling the calculation of the mass of reactants and products in chemical reactions.
Understanding the Mole

The mole concept is essential for determining how much of a substance is involved in a reaction. The amount of a substance in moles is directly related to its mass through the molar mass, which is the mass of one mole of a substance expressed in grams. By knowing the molar mass, you can convert between the mass of a substance and the number of moles.
- Example 1: To convert grams to moles, divide the mass of the substance by its molar mass.
- Example 2: To convert moles to grams, multiply the number of moles by the molar mass.
Applying Stoichiometry
Stoichiometric calculations are essential for determining the amount of reactants or products in a reaction. To perform stoichiometric calculations, you must first write a balanced chemical equation. The coefficients in the equation give the ratio of moles of each substance involved in the reaction, which can be used to find the amounts of substances needed or produced.
- Step 1: Write the balanced chemical equation for the reaction.
- Step 2: Convert known quantities (e.g., grams or liters) into moles using molar mass or molar volume.
- Step 3: Use the mole ratios from the balanced equation to find the unknown quantity.
For example, if you know the amount of a reactant, you can calculate how much product will be produced. Similarly, if you know the amount of a product, you can determine how much reactant is required. Stoichiometry also helps in limiting reactant problems, where you calculate which reactant will be fully consumed first and how much of the other reactant will be left over.
In summary, the mole concept and stoichiometry allow scientists to translate between the microscopic world of atoms and molecules and the macroscopic world of measurable quantities, making them indispensable tools in understanding and performing chemical reactions.
Kinetics and Rate Laws for Reactions
Understanding the speed at which reactions occur and the factors that influence this speed is essential for predicting the behavior of substances in various conditions. The study of how the concentration of reactants affects the rate of reaction is called kinetics. This area of study helps in determining the factors that control the rate, such as temperature, pressure, and the presence of catalysts, and how these elements interact to change the rate of a reaction.
In many reactions, the rate of reaction is not constant but depends on the concentration of reactants. The rate law expresses this relationship mathematically. It allows us to determine how the concentration of reactants influences the speed at which products are formed. The general form of a rate law is given by:
Rate = k [A]^m [B]^n
Here, k is the rate constant, and [A] and [B] represent the concentrations of the reactants. The exponents m and n are determined experimentally and represent the order of the reaction with respect to each reactant. Understanding these variables is crucial for predicting how changing concentrations will affect the reaction rate.
The reaction order can be determined through experimentation, and it can be classified as:
- Zero Order: The rate is independent of the concentration of the reactant.
- First Order: The rate is directly proportional to the concentration of one reactant.
- Second Order: The rate is proportional to the square of the concentration of one reactant or the product of two reactant concentrations.
In addition to concentration, temperature also plays a significant role in reaction kinetics. According to the Arrhenius equation, the rate constant k depends on temperature, and as temperature increases, the rate of most reactions also increases. The equation is as follows:
k = A e^(-Ea/RT)
Where A is the pre-exponential factor, Ea is the activation energy, R is the universal gas constant, and T is the temperature in Kelvin. This equation shows how the frequency of collisions and the energy required to overcome activation barriers affect the reaction rate.
Another important aspect of reaction rates is the role of catalysts. Catalysts are substances that increase the rate of reaction without being consumed in the process. They work by lowering the activation energy, allowing the reaction to proceed faster at a given temperature. Catalysts can be classified as either homogeneous (present in the same phase as the reactants) or heterogeneous (present in a different phase). Their effect on the rate of reaction can be significant, especially in industrial processes.
To summarize, understanding the kinetics and rate laws for reactions allows us to predict how changes in concentration, temperature, and the presence of catalysts will affect the speed of a reaction. By applying these principles, we can control reaction rates in various scientific and industrial applications, making them essential for both theoretical and practical purposes in many fields.
Solutions and Colligative Properties

The behavior of substances when dissolved in liquids is an important concept in various scientific fields. A solution forms when a solute dissolves in a solvent, creating a homogeneous mixture. The properties of solutions are influenced by the amount and type of solute, as well as the solvent’s characteristics. Among the many properties of solutions, colligative properties are particularly significant because they depend on the number of solute particles in the solution, rather than their chemical nature.
Colligative properties include freezing point depression, boiling point elevation, vapor pressure lowering, and osmotic pressure. These properties are all related to the number of solute particles present in the solution and not to the specific type of solute. As the concentration of solute particles increases, these properties are altered in a predictable way. Understanding these changes is crucial for practical applications, from antifreeze in cars to the functioning of biological cells.
Freezing Point Depression and Boiling Point Elevation
Two of the most commonly studied colligative properties are freezing point depression and boiling point elevation. Both of these properties describe how the presence of a solute affects the physical state of the solvent.
Freezing point depression occurs when the freezing point of a solvent is lowered by the addition of a solute. This happens because the solute particles interfere with the formation of a solid structure, making it harder for the solvent to freeze. The change in freezing point is directly proportional to the concentration of solute particles, and it can be calculated using the formula:
ΔTf = Kf × m × i
Where ΔTf is the change in freezing point, Kf is the freezing point depression constant for the solvent, m is the molality of the solute, and i is the van’t Hoff factor, which accounts for the number of particles the solute dissociates into.
Boiling point elevation, on the other hand, refers to the increase in the boiling point of a solvent when a solute is added. Just like freezing point depression, this phenomenon is a result of solute particles interfering with the solvent’s ability to evaporate. The boiling point elevation is given by the equation:
ΔTb = Kb × m × i
Where ΔTb is the change in boiling point, Kb is the boiling point elevation constant, m is the molality of the solute, and i is the van’t Hoff factor.
Osmotic Pressure and Vapor Pressure Lowering
Another important colligative property is osmotic pressure, which is the pressure required to stop the flow of solvent through a semipermeable membrane. Osmosis occurs when a solvent moves from an area of lower solute concentration to an area of higher solute concentration, in an attempt to equalize the concentrations. Osmotic pressure can be calculated using the formula:
π = i × M × R × T
Where π is the osmotic pressure, i is the van’t Hoff factor, M is the molarity of the solute, R is the gas constant, and T is the temperature in Kelvin.
Additionally, the addition of a solute to a solvent causes a lowering of the vapor pressure of the solvent. This occurs because the solute particles occupy surface space, reducing the number of solvent molecules able to escape into the vapor phase. This can be predicted by Raoult’s Law:
Psolution = Xsolvent × Psolvent
Where Psolution is the vapor pressure of the solution, Xsolvent is the mole fraction of the solvent, and Psolvent is the vapor pressure of the pure solvent.
Understanding these properties helps explain how substances behave in solutions and allows scientists to control and predict the effects of solute concentrations in various applications, from industrial processes to biological systems.
Chemical Bonding and Molecular Geometry
Understanding how atoms interact and bond to form molecules is fundamental to studying the properties and behavior of matter. The way in which atoms join together to create stable compounds is determined by the types of bonds they form and the arrangement of atoms in the resulting structure. These factors directly influence the physical and chemical characteristics of the substance. The geometry of molecules, or molecular structure, is key to understanding the interactions between atoms and how molecules behave in different environments.
Bonds can be classified into different types based on how electrons are shared between atoms. These include ionic bonds, covalent bonds, and metallic bonds. The arrangement of atoms within a molecule, also known as molecular geometry, is determined by the electron pairs and bonds around a central atom. This shape affects how molecules interact with each other and with external forces, such as light or heat. Understanding these concepts allows for the prediction of molecular behavior in various chemical reactions and physical processes.
Types of Chemical Bonds
There are three primary types of bonds that hold atoms together in a molecule. Each type of bond has distinct characteristics that influence the properties of the resulting compound.
- Ionic Bonds: These bonds form when electrons are transferred from one atom to another, resulting in the formation of positively and negatively charged ions. The electrostatic attraction between these ions holds the compound together.
- Covalent Bonds: In covalent bonding, electrons are shared between two atoms. This sharing allows both atoms to achieve a stable electron configuration, typically resulting in the formation of nonmetals or molecules.
- Metallic Bonds: Found in metals, these bonds involve the sharing of free-moving electrons between many atoms, allowing for properties like electrical conductivity and malleability.
Molecular Geometry and VSEPR Theory

The shape of a molecule is crucial for understanding its chemical behavior and interactions. One of the most widely used methods to predict molecular geometry is Valence Shell Electron Pair Repulsion (VSEPR) theory. According to this theory, electron pairs around a central atom arrange themselves in a way that minimizes repulsion, leading to a specific molecular shape.
The basic steps to predict the shape of a molecule involve counting the number of bonding pairs and lone pairs of electrons around the central atom. The resulting electron pair geometry determines the arrangement of atoms, which in turn influences the physical and chemical properties of the molecule.
- Linear: When there are two bonding pairs and no lone pairs, the molecule adopts a linear shape (e.g., CO2).
- Trigonal Planar: Three bonding pairs and no lone pairs result in a trigonal planar shape (e.g., BF3).
- Tetrahedral: Four bonding pairs and no lone pairs lead to a tetrahedral arrangement (e.g., CH4).
- Trigonal Bipyramidal: Five bonding pairs lead to this geometry (e.g., PCl5).
- Octahedral: Six bonding pairs lead to an octahedral structure (e.g., SF6).
In addition to the ideal geometries predicted by VSEPR, the presence of lone pairs can distort these shapes, as lone pairs occupy more space and push bonding pairs closer together. This results in variations in the molecular geometry that must be considered for a more accurate description.
Important Constants and Their Values
In the study of physical sciences, certain numerical values, known as constants, play a critical role in the equations and calculations that describe the behavior of matter. These constants are universal, meaning they remain the same regardless of the conditions or the substance involved. They form the foundation for a wide range of scientific principles and are essential for solving problems in various fields of science. Understanding and memorizing these constants is crucial for students and professionals alike, as they are frequently used in problem-solving and theoretical work.
Key Physical Constants

The following constants are commonly encountered in various scientific calculations. Knowing their values is essential for conducting precise and accurate experiments or solving problems related to different physical processes.
- Speed of Light (c): 299,792,458 m/s
- Gravitational Constant (G): 6.67430 × 10-11 m3kg-1s-2
- Planck’s Constant (h): 6.62607015 × 10-34 J·s
- Avogadro’s Number (NA): 6.02214076 × 1023 mol-1
- Boltzmann Constant (kB): 1.380649 × 10-23 J/K
Constants Related to Thermodynamics
Thermodynamic constants are used to describe the behavior of energy and matter under various conditions, and they are indispensable in the study of heat and work interactions within a system.
- Universal Gas Constant (R): 8.314 J/(mol·K)
- Standard Atmosphere (atm): 101.325 kPa
- Faraday Constant (F): 96,485 C/mol
- Standard Enthalpy of Formation (ΔHf): varies for each compound
These constants, among others, are pivotal in performing accurate calculations, especially when working with equations that describe the fundamental forces of nature, thermodynamic systems, and molecular structures. Familiarity with their values ensures efficiency in scientific work and enhances the understanding of physical laws and their applications.