
In this section, we dive into the fundamental principles and problems that lay the foundation for advanced topics in mathematics. By breaking down each concept, we can approach the material with clarity and precision, making complex ideas more accessible. Whether you’re a student looking to strengthen your skills or someone revisiting the subject, this guide will help you navigate through the most important aspects with ease.
Breaking down complex problems into smaller, manageable steps is crucial. With the right approach, even the most challenging exercises can become straightforward. This section offers a structured way to grasp essential techniques and methods that can be applied to similar problems. By the end, you’ll have a clearer understanding of how to tackle various types of questions.
Through detailed explanations and examples, we aim to provide a solid grasp of the material. You’ll gain valuable insights into how to approach and solve problems effectively. Each step is designed to enhance your problem-solving ability and improve your overall comprehension.
Core Connections Course 1 Chapter 2 Answers
This section focuses on solving key problems and mastering the concepts presented in the second part of the program. It provides essential techniques and strategies that guide learners through the most challenging exercises. By understanding the underlying principles, students can approach these problems with greater confidence and accuracy.
Each solution is broken down into clear steps, helping learners see the logical flow required to solve complex tasks. This approach ensures that the material is both approachable and manageable. Understanding the process behind each solution is crucial for applying similar techniques to new problems in the future.
By revisiting the fundamental methods and strategies outlined here, students can strengthen their problem-solving skills and build a solid foundation for more advanced topics. These solutions not only offer the correct approach but also reinforce the skills needed for continued success in the subject.
Overview of Core Connections Course 1
This section introduces the foundational elements designed to build a strong understanding of key mathematical concepts. The material is carefully structured to guide learners from basic principles to more advanced problem-solving techniques. Each topic is aimed at enhancing critical thinking and applying mathematical methods to real-world scenarios.
The program focuses on essential areas that help learners gain a deep grasp of the subject. Key goals include:
- Understanding basic mathematical operations and their applications
- Developing problem-solving strategies that can be applied to various challenges
- Strengthening analytical thinking to approach complex tasks with confidence
- Fostering skills that are necessary for success in higher-level mathematics
Throughout the lessons, learners will encounter progressively more difficult exercises that challenge them to apply the methods they have learned. Each problem is presented in a clear and logical sequence to help build proficiency and ensure mastery of the concepts.
Key Learning Objectives in Chapter 2
The focus of this section is on strengthening foundational skills and building a deeper understanding of mathematical concepts. Learners will work through a series of key objectives designed to deepen their problem-solving abilities and enhance their grasp of core techniques. The goal is to master these essential skills and use them effectively in different contexts.
By the end of this unit, students should be able to:
- Recognize patterns and apply them to solve problems efficiently
- Understand the relationship between different mathematical concepts
- Use logical reasoning to break down complex problems into simpler steps
- Apply mathematical techniques to real-world scenarios and practical situations
These objectives aim to provide learners with the necessary tools to succeed in subsequent levels and develop a comprehensive understanding of the material. The exercises and tasks will build on each objective to ensure a progressive and thorough mastery of the subject matter.
Step-by-Step Solutions for Chapter 2

This section provides a detailed guide to solving problems from the second unit of the program. Each problem is broken down into manageable steps, allowing learners to follow along and gain a clear understanding of the process behind each solution. The goal is to make each task approachable and ensure that learners grasp the techniques needed to solve similar problems on their own.
Example 1: Solving Equations
To solve the first set of equations, follow these steps:
- Identify the variable and constants in the equation.
- Isolate the variable by performing inverse operations on both sides.
- Simplify the equation until the variable is solved.
- Check the solution by substituting the value back into the original equation.
Example 2: Word Problem Breakdown
For word problems, it’s essential to first translate the text into a mathematical expression. Here’s how to approach it:
- Read the problem carefully and identify key information (numbers, relationships, etc.).
- Convert the information into an equation or system of equations.
- Use known methods to solve the equation.
- Interpret the result in the context of the problem.
By following these structured steps, you can systematically approach each problem, making complex tasks easier to solve and understand.
Understanding Important Concepts in Chapter 2
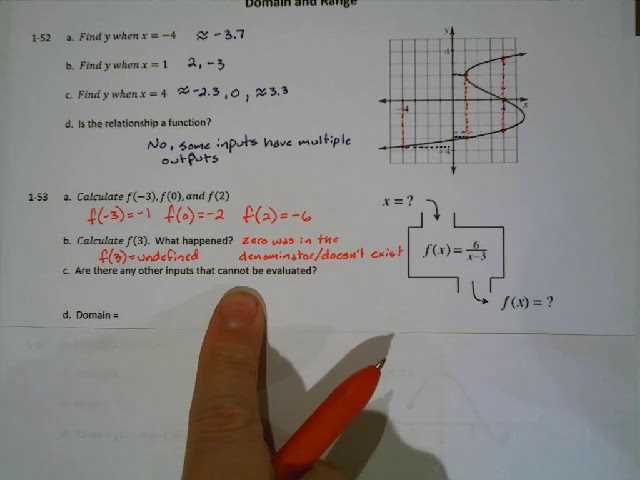
In this section, we focus on the key principles that form the foundation of the material. These concepts are essential for solving problems and applying mathematical techniques accurately. A deep understanding of these ideas will enable learners to approach more complex topics with confidence and clarity.
Key Idea 1: Solving Linear Equations
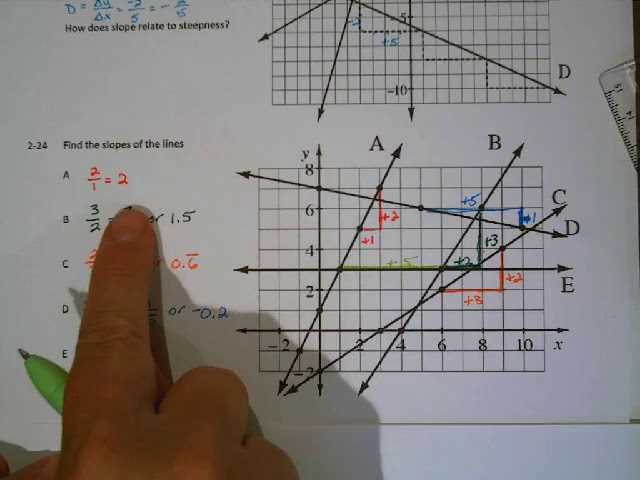
One of the main concepts in this unit is mastering the process of solving linear equations. These equations involve variables and constants, and the goal is to isolate the variable on one side of the equation. Understanding how to manipulate the equation step by step is crucial for solving them correctly.
- Isolate the variable using inverse operations.
- Simplify both sides of the equation.
- Check the solution by substituting the value back into the equation.
Key Idea 2: Working with Ratios and Proportions
Another important concept is understanding ratios and proportions. These are relationships between two quantities and can be used to solve a variety of practical problems. Mastering this concept helps in comparing different values and understanding their relative sizes.
- Write ratios as fractions or as a colon notation.
- Set up proportions to solve for unknown quantities.
- Use cross-multiplication to find the missing value.
By internalizing these core ideas, learners can develop the necessary skills to tackle more advanced topics in the subject.
Common Mistakes to Avoid in Chapter 2

As learners work through the material, it’s important to be aware of common pitfalls that can hinder progress. Understanding these mistakes and learning how to avoid them will help improve accuracy and boost problem-solving skills. By being mindful of these errors, students can tackle tasks with greater confidence and avoid unnecessary setbacks.
Overlooking Simple Operations

One of the most frequent mistakes is neglecting basic operations, such as addition, subtraction, multiplication, and division, when solving equations. It’s easy to rush through these steps, but failing to carefully perform these operations can lead to incorrect results.
- Always double-check calculations at each step.
- Be cautious when handling negative numbers or fractions.
- Ensure that each operation is performed correctly before moving forward.
Misinterpreting Word Problems
Another common error is misunderstanding the context or misinterpreting the information given in word problems. Students often struggle to translate a real-world scenario into a mathematical equation, which can lead to confusion and mistakes.
- Carefully read the entire problem before attempting to solve it.
- Highlight key information and translate it into a mathematical expression.
- Break down the problem into smaller, manageable parts to ensure clarity.
By staying vigilant and avoiding these common mistakes, students can improve their ability to solve problems accurately and efficiently.
Detailed Explanations for Each Problem
In this section, we provide thorough explanations for each problem to ensure a clear understanding of the process behind the solutions. The aim is to guide students step-by-step, so they can grasp the logic and techniques used to arrive at the correct answers. Each solution is broken down into manageable steps, making it easier to follow and apply the same methods to other problems.
Example 1: Solving Linear Equations

For this example, we will solve a simple linear equation. The process involves isolating the variable on one side of the equation and simplifying both sides. Here’s how to approach it:
- Start with the equation: 2x + 5 = 15.
- Subtract 5 from both sides: 2x = 10.
- Divide both sides by 2 to isolate x: x = 5.
- Check the solution by substituting x = 5 back into the original equation.
Example 2: Working with Proportions
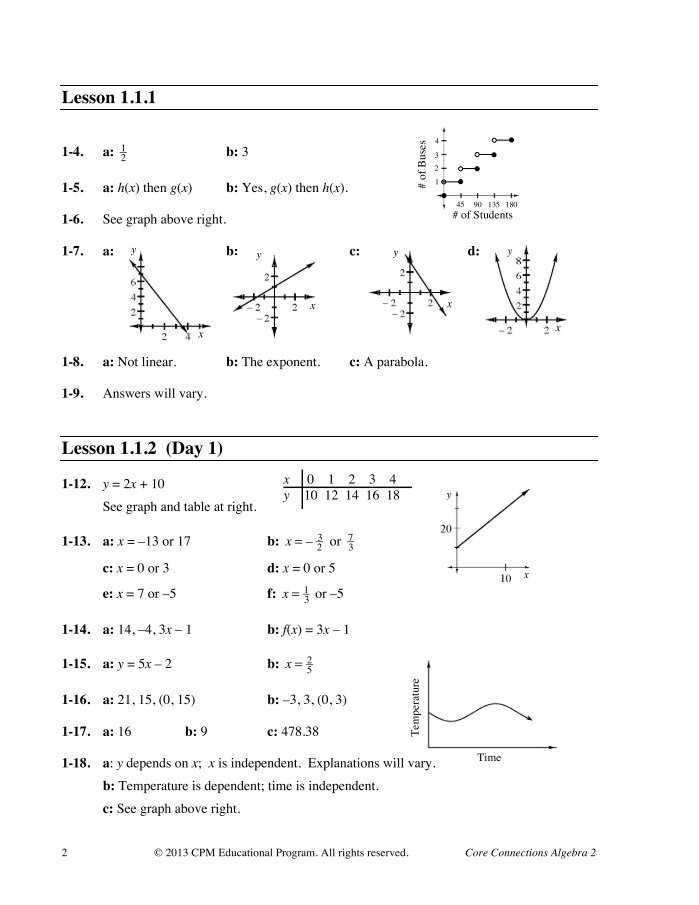
In this example, we solve a proportion problem. The key is to set up a ratio and use cross-multiplication to find the unknown value. Follow these steps:
- Write the proportion: 3/4 = x/8.
- Cross-multiply: 3 * 8 = 4 * x.
- Solve for x: 24 = 4x, so x = 6.
- Check the result by substituting x = 6 into the original proportion.
By following these clear and structured explanations, learners can develop a deeper understanding of how to approach different types of problems with confidence and accuracy.
How to Approach Core Connections Problems
When faced with mathematical problems, it’s important to have a clear strategy to break them down into manageable steps. A structured approach not only helps in solving the problems correctly but also builds confidence in handling similar tasks. By following a logical sequence, learners can tackle even the most complex questions effectively.
Step-by-Step Problem-Solving Process
Here is a simple approach to solving mathematical problems, ensuring clarity and precision in each step:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and identify key information (numbers, variables, and operations). |
| 2 | Translate the problem into a mathematical expression or equation. |
| 3 | Perform the necessary operations in the correct order (PEMDAS/BODMAS). |
| 4 | Isolate the variable and simplify both sides of the equation. |
| 5 | Double-check your calculations and verify the solution. |
Tips for Effective Problem-Solving

- Always double-check the units and variables involved in the problem.
- Be mindful of common pitfalls, such as misinterpreting the problem or overlooking negative signs.
- Break complex problems into smaller, simpler parts for easier management.
- Work through a similar example first to build confidence before tackling the main problem.
By following this systematic approach, learners can improve their problem-solving skills and approach each task with a methodical mindset.
Critical Thinking Strategies for Success
In order to excel in solving complex problems, it’s essential to develop strong critical thinking skills. These strategies not only help to approach tasks in a more organized way but also improve decision-making and problem-solving abilities. By applying logical reasoning and analyzing different perspectives, learners can make informed choices and find effective solutions.
Key Strategies for Strengthening Critical Thinking
The following strategies can guide learners in sharpening their critical thinking skills and improving their problem-solving techniques:
| Strategy | Description |
|---|---|
| Clarify the Problem | Break down complex problems into simpler parts, ensuring that you understand the key concepts before attempting to solve them. |
| Consider Multiple Approaches | Explore different methods and solutions to a problem, as this can lead to more effective or efficient outcomes. |
| Analyze and Evaluate | Assess the validity and reliability of the information provided, and ensure that your reasoning is based on sound evidence. |
| Ask Questions | Don’t hesitate to ask clarifying questions or seek further details when something is unclear or confusing. |
| Reflect on the Process | After completing the task, take time to review your reasoning and the steps taken, identifying areas for improvement. |
Building Strong Analytical Skills
Critical thinking is a skill that improves with practice. By regularly challenging oneself to analyze situations from various angles and question assumptions, learners will become more adept at making sound decisions and tackling problems effectively. These skills are not only useful in academic settings but also in real-world scenarios.
Incorporating these strategies into everyday problem-solving will ultimately foster success and ensure better outcomes in both academic and practical challenges.
Tips for Mastering Chapter 2 Material
To excel in mastering the concepts presented in this section, it’s crucial to approach the material with focus and a structured strategy. Understanding the underlying principles and practicing regularly will greatly enhance your ability to retain information and apply it effectively in different scenarios. Here are some key strategies to help you succeed in mastering the content.
- Focus on Key Concepts: Identify the core ideas and focus on understanding them thoroughly. Building a solid foundation will make it easier to grasp more complex topics later.
- Practice Regularly: Consistent practice is essential for reinforcing new skills and concepts. Work through practice problems to strengthen your understanding and increase your confidence.
- Break Down Complex Problems: Don’t be overwhelmed by challenging problems. Break them down into smaller, more manageable steps and tackle them one at a time.
- Ask Questions: If you’re unsure about a concept or solution, ask for clarification. Engaging with instructors or peers can offer new perspectives and help clear up confusion.
- Review Mistakes: Review errors to understand where you went wrong. Analyzing your mistakes will improve your problem-solving skills and help avoid repeating the same errors.
- Use Supplementary Resources: Sometimes, additional resources such as online tutorials, videos, or textbooks can offer a different explanation that makes complex topics easier to understand.
By incorporating these strategies into your study routine, you’ll not only master the material but also build confidence in your problem-solving abilities, ensuring long-term success in future lessons.
Real-World Applications of Core Connections
The concepts and skills developed in mathematical exercises have far-reaching implications beyond the classroom. By applying these principles in real-world situations, learners can solve practical problems and make informed decisions. Understanding how mathematical ideas are used in everyday life can motivate students to master the material while recognizing its value outside of academic contexts.
Everyday Examples Where Math is Used
Mathematics is present in many aspects of daily life. Below are some common areas where mathematical principles are applied:
- Personal Finance: Budgeting, saving, and managing expenses all require knowledge of percentages, ratios, and basic algebra.
- Technology and Engineering: From designing new gadgets to creating software, engineering relies heavily on advanced mathematical concepts such as geometry and calculus.
- Health and Medicine: Medical professionals use statistical analysis to interpret research, while dosage calculations rely on accurate arithmetic and fractions.
- Construction and Architecture: Builders use geometric principles to plan spaces, and architects apply complex calculations for structural integrity and design.
- Business and Economics: Companies use mathematical modeling to predict trends, optimize operations, and make data-driven decisions.
How Mathematical Skills Enhance Problem-Solving
In many professional fields, the ability to break down problems into smaller, manageable steps is essential. Mathematical reasoning helps in identifying patterns, formulating hypotheses, and finding solutions to challenges. Whether working in finance, technology, or even the arts, applying mathematical principles can lead to more efficient and effective results. These skills also foster critical thinking, which is valuable in any profession or everyday situation.
By linking classroom knowledge to real-world applications, students can appreciate the practical benefits of mastering mathematical concepts and how they influence various industries and personal decisions.
Study Techniques for Success
Achieving mastery in any subject requires more than just passive reading–it demands focused effort and strategic study habits. To fully understand the material and apply it effectively, it’s important to develop efficient techniques that enhance both comprehension and retention. Below are several proven strategies for achieving success in any academic pursuit.
- Active Learning: Engage actively with the material rather than just reading passively. Take notes, ask questions, and discuss concepts with peers or instructors to deepen your understanding.
- Practice Regularly: Consistent practice is key. Work through problems or exercises regularly to reinforce learning and build problem-solving skills. Repetition helps solidify concepts in your memory.
- Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller steps. Tackle each part separately and methodically. This approach helps reduce anxiety and ensures a thorough understanding of each step.
- Teach What You Learn: One of the best ways to ensure understanding is to teach the material to someone else. Explaining complex concepts in simple terms helps reinforce your knowledge and highlight areas needing improvement.
- Use Visual Aids: Diagrams, charts, and other visual aids can help clarify complex ideas and make abstract concepts more concrete. Visual learning enhances memory retention and aids in understanding relationships between ideas.
- Review Regularly: Don’t wait until the last minute to study. Instead, review material regularly to ensure it stays fresh in your mind. Spaced repetition is an effective way to prevent forgetting and solidify long-term retention.
By implementing these study techniques, you will be better equipped to navigate through any academic challenge. Whether you’re tackling a difficult problem or preparing for an exam, these habits will build a strong foundation for success and help you master the material effectively.
Resources to Enhance Your Learning
To truly master any subject, it’s essential to go beyond textbooks and lessons. There are a wealth of resources available that can provide different perspectives, practical examples, and interactive opportunities to deepen your understanding. Whether you’re looking for additional practice problems, video tutorials, or tools to reinforce concepts, these resources can significantly enhance your learning experience.
Helpful Tools and Platforms
| Resource | Description |
|---|---|
| Online Learning Platforms | Platforms like Khan Academy, Coursera, and edX offer free courses and tutorials in a variety of subjects. These provide step-by-step instructions, practice exercises, and expert explanations to strengthen your grasp of key concepts. |
| Interactive Practice Sites | Websites such as Quizlet and Brainscape allow you to create custom flashcards and quizzes, enabling you to actively engage with material and test your knowledge in real-time. |
| YouTube Channels | There are many educational YouTube channels like CrashCourse, PatrickJMT, and Professor Leonard that explain complex topics in an easy-to-understand format, often with visual aids and examples. |
| Study Groups | Joining study groups, either online or in person, allows you to collaborate with peers. Teaching and learning from others can help solidify your knowledge and provide new insights into challenging material. |
| Math-Specific Tools | For mathematics learners, tools like Wolfram Alpha and Desmos offer calculators and problem solvers that can help visualize solutions and break down steps to find answers. |
Printed and Digital Resources
- Textbooks and Workbooks: Don’t underestimate the value of a good textbook or workbook. They often provide detailed examples, practice problems, and solutions to help reinforce your understanding.
- Online Forums and Communities: Websites like StackExchange or Reddit’s learning communities are great places to ask questions, get advice, and interact with others who are studying similar topics.
- Study Apps: Apps such as Notion, Evernote, or OneNote can help organize notes, create to-do lists, and track your progress across different subjects.
By taking advantage of these various resources, you can make your learning experience more engaging and effective. Each tool offers a unique way to approach difficult concepts, ensuring you have multiple ways to reinforce your knowledge and build a deeper understanding of the material.
Interactive Tools for Better Understanding

In today’s learning environment, interactive tools play a crucial role in helping students grasp complex concepts more effectively. These tools provide a hands-on approach, allowing learners to visualize problems, simulate scenarios, and practice in a dynamic way. Whether through online platforms, apps, or interactive websites, these resources can transform passive learning into an engaging and active process, making difficult topics more approachable.
Popular Interactive Platforms
Several platforms offer interactive learning experiences that cater to different types of learners. From solving problems step-by-step to visualizing mathematical graphs, these tools help build a deeper understanding of concepts by providing immediate feedback and real-time practice.
- Wolfram Alpha: An advanced computational engine that helps users solve complex problems in mathematics, physics, and many other subjects. It offers step-by-step solutions, helping users understand how to arrive at the answer.
- Desmos Graphing Calculator: This online tool allows students to visualize mathematical equations, making it easier to understand concepts like algebra, calculus, and geometry through dynamic graphs.
- GeoGebra: A free platform that integrates geometry, algebra, spreadsheets, and calculus into an interactive environment. It is a valuable resource for visualizing math concepts in real-time.
Interactive Apps and Websites
In addition to web-based platforms, there are many apps and websites that allow students to engage with the material directly. These resources can help learners practice problems, track their progress, and receive feedback instantly.
- Quizlet: A flashcard-based app that helps users learn vocabulary, formulas, and concepts through repetition and active recall. It also allows students to create their own flashcards.
- Edpuzzle: An interactive learning tool that integrates video lessons with questions. It allows educators to track student engagement and comprehension while students watch videos and answer embedded questions.
- Khan Academy: Offers interactive exercises and video tutorials on a variety of subjects, providing instant feedback and personalized practice to help learners progress at their own pace.
By incorporating these interactive tools into your study routine, you can enhance your comprehension, reinforce important concepts, and gain the confidence needed to tackle challenging material. These resources foster a more personalized learning experience, encouraging both independent learning and collaboration.
How to Check Your Answers Effectively
Reviewing and verifying your work is an essential step in the learning process. Ensuring accuracy not only boosts your confidence but also helps reinforce your understanding of the material. A well-structured approach to checking your responses can save time and prevent mistakes, ensuring that you grasp key concepts clearly. By using systematic techniques, you can identify errors, correct misunderstandings, and deepen your knowledge.
1. Break Down Each Problem
When checking your solutions, start by breaking down each problem into smaller, manageable parts. This allows you to focus on specific steps or operations, ensuring that no detail is overlooked. Review the logic behind each step, verify the accuracy of calculations, and check if the final result aligns with the expected outcome. This step-by-step analysis is particularly effective for complex problems that require multiple operations.
2. Use Alternative Methods
If possible, apply a different method to solve the problem and compare the results. For example, if you used algebraic manipulation in one solution, try using graphical methods or estimation to verify your answer. This approach can help you identify inconsistencies or errors that may have been missed during the initial attempt.
3. Cross-Check With Reliable Resources
Refer to textbooks, online resources, or practice problems to cross-check your answers. Reliable sources can provide examples of similar problems and solutions, helping you gauge whether your approach and results are correct. Sometimes, comparing your work with worked-out examples can highlight mistakes or show alternative, more efficient methods.
4. Work With Peers or Educators
Collaborating with others can provide valuable feedback. Share your solutions with classmates, teachers, or online study groups to see if they arrive at the same conclusions. Peer review often helps identify common mistakes or misunderstandings that you may have missed. Constructive criticism can also suggest better methods or alternative solutions to problems.
5. Take Time to Reflect
After reviewing your work, take a moment to reflect on your approach and the steps you took to solve the problem. Ask yourself questions like, “Does this solution make sense?” or “Is there a simpler way to approach this?” This self-reflection promotes critical thinking and helps consolidate your understanding of the material.
By following these steps, you can check your solutions thoroughly and effectively. A structured review process not only ensures that your answers are correct but also improves your problem-solving skills over time, leading to greater success in mastering the material.
Final Review of Chapter 2 Key Points

As you prepare to move forward, it’s important to consolidate your understanding of the material covered. A final review helps ensure that the key concepts are clear and that you’ve absorbed the most critical information. This process not only strengthens your grasp of the content but also highlights areas that may require additional focus before progressing. Here, we summarize the main ideas and skills that were explored in this section.
1. Understanding Fundamental Concepts
At the core of this section are essential ideas that serve as the foundation for more advanced topics. Whether it’s mathematical principles, problem-solving techniques, or logical reasoning, reinforcing these fundamental concepts is key to your overall success. Review the definitions, formulas, and steps involved in solving basic problems, as these will form the basis for tackling more complex challenges.
2. Mastery of Key Problem-Solving Techniques
Throughout the section, you have learned a variety of methods to approach problems. Whether it’s working through equations, analyzing patterns, or applying different strategies, mastering these techniques will make problem-solving more efficient and effective. Pay particular attention to the specific steps involved in each method and practice applying them in different scenarios.
3. Application of Learning to Real-World Problems
A significant part of this section involved applying your skills to real-world situations. Understanding how the material you learned can be applied outside of a textbook context enhances your ability to use this knowledge practically. Reflect on how the concepts discussed might relate to real-life scenarios, and think about how the skills can be used in problem-solving beyond the classroom.
4. Common Mistakes and How to Avoid Them
It’s important to recognize the common errors that students often make while learning these concepts. Whether it’s misinterpreting a problem, overlooking key details, or rushing through calculations, being aware of these pitfalls will help you avoid them in the future. Review the strategies for checking your work carefully to ensure that these mistakes are minimized.
5. Reinforcement Through Practice
Repetition is one of the most effective ways to solidify your understanding. By practicing problems of varying difficulty, you not only improve your confidence but also deepen your understanding of how to apply the material in different contexts. Take the time to go through additional exercises, and don’t hesitate to revisit any areas that feel unclear.
By reviewing these key points, you are setting yourself up for success. Continue practicing, ask questions when necessary, and use your understanding as a stepping stone to tackle more advanced challenges in the future. A solid grasp of these concepts will serve you well as you move forward in your studies.