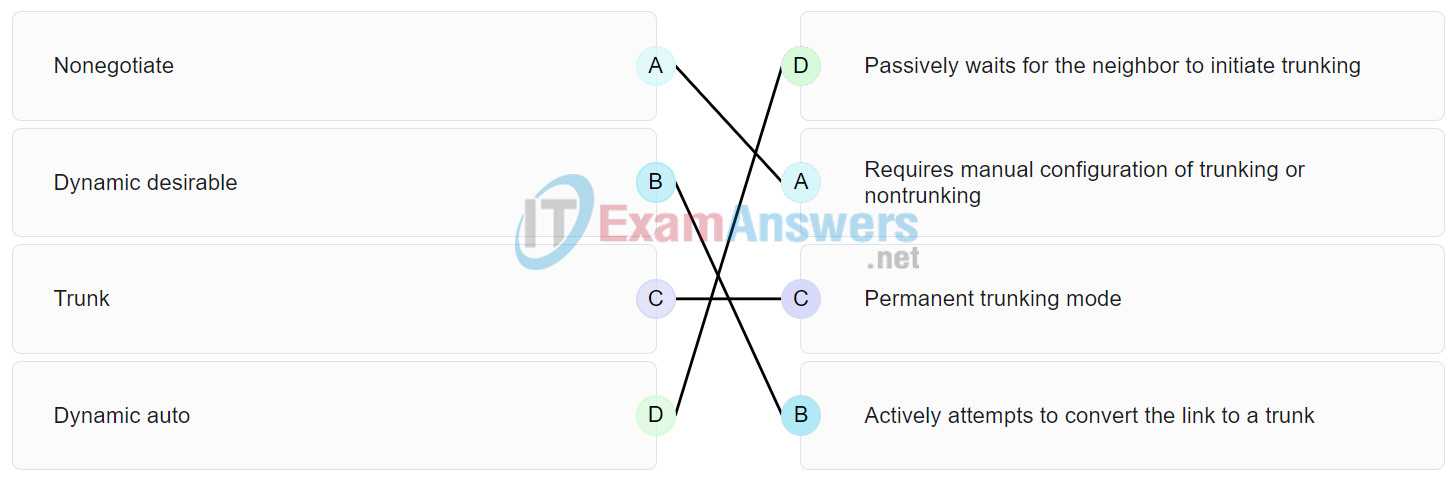
In this section, we will explore essential concepts and provide step-by-step guidance on solving problems related to advanced mathematical techniques. These skills form the foundation for tackling more complex topics in the subject, and mastering them will greatly enhance problem-solving abilities.
Focus is placed on improving logical reasoning and applying appropriate methods to reach accurate solutions. By understanding the underlying principles, learners can confidently approach and solve different types of exercises.
Throughout the discussion, we will break down difficult concepts into manageable parts, helping to build a solid grasp of the material. The goal is not just to find the right answers but to develop a deeper comprehension of the methods behind them.
Core Connections Course 2 Chapter 6 Answers
This section focuses on helping students gain a deeper understanding of the mathematical principles and techniques required to solve a variety of problems. The objective is to explore the underlying processes and strategies that lead to the correct outcomes, enabling learners to tackle exercises with confidence and precision.
The exercises covered here involve critical thinking and methodical approaches, emphasizing the importance of step-by-step problem-solving. By breaking down complex tasks into simpler components, students can build a strong foundation for more advanced concepts in the future.
Breaking Down Complex Problems
Understanding how to approach and break down complex problems is a key skill. In this section, students will learn how to analyze each question systematically, identifying important variables and applying relevant methods to reach logical solutions. The process of simplification plays a major role in ensuring clarity and efficiency when solving mathematical challenges.
Applying Mathematical Techniques
Mastering various techniques is essential for success in solving problems effectively. The section explores how to apply algebraic rules, solve equations, and use other mathematical operations correctly. By practicing these methods repeatedly, learners will improve their ability to approach future problems with greater ease and accuracy.
Understanding Key Concepts in Chapter 6
This section focuses on exploring essential ideas that form the basis of the exercises and problem-solving methods. Understanding these fundamental concepts is critical for mastering the material and successfully applying them to different types of problems.
At the heart of this section is the importance of grasping how mathematical principles are interlinked. By connecting theory with practical application, students can see how abstract ideas translate into real-world solutions.
Key Ideas to Master
- Identifying patterns and relationships between variables
- Understanding the rules governing mathematical operations
- Applying critical thinking to simplify complex problems
- Developing a logical approach to find solutions
Practical Application of Concepts
Once the key principles are understood, the next step is to apply them in problem-solving scenarios. By following specific steps and using mathematical tools, students can achieve the correct results more efficiently.
- Break down problems into manageable parts
- Identify the most relevant mathematical operations
- Apply the appropriate methods to solve each part
- Combine results to reach the final solution
Steps to Solve Chapter 6 Problems
To effectively tackle the exercises in this section, it is essential to follow a structured approach. By breaking down problems into manageable steps, students can ensure that each part is addressed thoroughly and correctly. This methodical approach helps build confidence and enhances accuracy in problem-solving.
Understanding the problem, identifying the right techniques, and executing them systematically are key to achieving the desired results. With practice, students will improve their ability to work through similar tasks in the future.
Step-by-Step Approach
- Read and understand the problem: Carefully review all given information and identify the goal of the problem.
- Identify relevant concepts: Determine which mathematical principles or formulas apply to the problem.
- Break down the problem: Divide the task into smaller, more manageable parts to simplify the solution process.
- Choose the correct method: Decide on the most efficient mathematical operation or approach to solve each part.
- Perform calculations: Execute the necessary steps, keeping track of each operation and its results.
Finalizing the Solution
- Verify your work: Double-check each step to ensure the calculations are accurate and complete.
- Combine results: If the problem requires multiple steps, combine the intermediate results to reach the final answer.
- Interpret the solution: Make sure that the final result answers the original question and is logically sound.
Important Formulas for Chapter 6

In this section, we will explore the essential equations and relationships that are crucial for solving the problems presented. Mastering these formulas will provide the foundation for tackling a variety of exercises and enable students to solve problems with confidence and precision.
Formulas serve as tools that simplify complex tasks and allow for systematic problem-solving. Understanding when and how to use them effectively is key to achieving accurate results. By practicing the application of these formulas, learners can ensure that they are well-prepared for similar challenges in the future.
- Equation 1: The basic equation for solving linear problems, used to isolate variables and solve for unknowns.
- Equation 2: A formula for calculating the area of geometric shapes, essential for understanding spatial relationships.
- Equation 3: The proportionality equation that is often used to solve ratio and proportion problems.
- Equation 4: A formula for converting between units, ensuring consistency in measurements.
By familiarizing yourself with these formulas and practicing their application, you will gain a stronger understanding of how to approach problems more efficiently. Always remember to review the steps involved in applying each formula, as this will help avoid mistakes and lead to better accuracy.
Common Mistakes in Core Connections
While solving problems in this section, students often make several recurring errors that can hinder their understanding and lead to incorrect results. Identifying and avoiding these mistakes is crucial for mastering the material and improving overall performance. By being aware of these common pitfalls, learners can develop more effective problem-solving strategies.
Many of these mistakes occur during the application of key concepts, such as misinterpreting the problem, overlooking essential details, or using the wrong method. Addressing these issues early on can help prevent confusion and ensure greater accuracy in future tasks.
Common Errors to Watch For
- Misunderstanding the Problem: Failing to fully comprehend what the question is asking can lead to using incorrect methods or operations.
- Incorrect Application of Formulas: Using the wrong formula for a given situation or misapplying mathematical rules is a frequent mistake.
- Forgetting to Simplify: Overlooking the importance of simplifying expressions can result in complicated and unnecessary calculations.
- Neglecting to Double-Check Work: Not reviewing steps or solutions may lead to avoidable errors that could be easily spotted with a second look.
Avoiding These Mistakes
- Read Carefully: Always take the time to read the problem thoroughly and ensure you understand what is being asked.
- Stay Organized: Write down each step clearly, and check that each calculation follows logically from the previous one.
- Use the Right Methods: Always select the appropriate formulas or techniques that match the problem’s requirements.
- Review Your Work: Before finalizing your answer, double-check each step to avoid simple errors in calculations.
Effective Strategies for Chapter 6

Successfully navigating through this section requires a strategic approach that enhances both comprehension and problem-solving efficiency. By implementing effective methods, students can tackle complex problems more easily and ensure that their understanding of key concepts is solid. The right strategies not only help in solving individual exercises but also build a strong foundation for future learning.
These techniques focus on breaking down problems into simpler steps, prioritizing understanding over memorization, and reinforcing learning through consistent practice. Developing a clear strategy for each problem will streamline the process and lead to better results.
- Focus on Understanding Concepts: Before diving into exercises, ensure a solid understanding of the underlying principles. This allows for more flexible problem-solving.
- Break Problems into Smaller Parts: Divide complex problems into manageable sections. Solve each part individually to avoid feeling overwhelmed.
- Practice Regularly: The more you practice, the more comfortable you will become with the material. Consistent practice solidifies concepts and speeds up problem-solving.
- Stay Organized: Keep your work neat and organized, writing down each step clearly. This reduces errors and helps track your thought process.
By applying these strategies, learners can approach each exercise with more confidence and clarity, ultimately improving both their skills and their overall understanding of the subject matter.
Real-Life Applications of Chapter 6 Skills
The skills learned in this section are not just limited to solving textbook problems; they have wide-ranging applications in real-world scenarios. Understanding these concepts can help individuals approach everyday challenges more effectively, whether it’s in professional settings, personal projects, or even daily decision-making.
By applying these principles to real-life situations, learners can see how abstract ideas become useful tools for solving practical problems. This practical application not only reinforces understanding but also demonstrates the value of these skills in various contexts.
Practical Use in Personal Finances
The ability to analyze and solve problems using mathematical techniques is essential in managing personal finances. From budgeting and managing expenses to calculating loan interest rates and savings growth, the skills learned can help individuals make informed decisions and better plan their financial future.
Applications in Professional Fields

In many industries, professionals rely on similar mathematical principles to make decisions. Engineers, architects, and scientists frequently apply the same techniques to design, analyze, and solve complex problems. Mastering these methods helps build the problem-solving mindset needed in these careers.
How to Improve Problem-Solving Speed
Increasing the speed at which you solve problems is an essential skill, particularly when facing time constraints or high-pressure situations. By refining your approach and practicing specific techniques, you can boost both your efficiency and accuracy. Developing a faster problem-solving ability involves more than just speeding through steps–it’s about understanding the underlying patterns and applying the most effective strategies quickly.
The key to faster problem-solving lies in recognizing common patterns, avoiding unnecessary steps, and having a clear plan of action for each problem. With consistent practice and the right mindset, you can become more adept at tackling complex problems swiftly and confidently.
- Practice Regularly: The more you practice, the faster you become. Consistent repetition helps solidify methods and improves recall under pressure.
- Master Key Concepts: Having a strong grasp of fundamental principles allows you to recognize problems more quickly and apply solutions without hesitation.
- Break Problems into Steps: Instead of attempting to solve everything at once, break problems into smaller, manageable parts to save time.
- Learn Shortcuts: Find faster ways to solve common problem types, such as using mental math or simplifying expressions before performing operations.
By integrating these strategies into your study routine, you will notice a significant improvement in the speed at which you can approach and solve problems. The more you practice with intention, the more natural and efficient your problem-solving process will become.
Detailed Walkthrough of Sample Problems
This section provides a step-by-step breakdown of sample exercises to illustrate how to approach and solve them effectively. By examining these examples in detail, students can gain a deeper understanding of the processes involved and learn to apply similar strategies to different problems. Each step in the walkthrough highlights key techniques, ensuring that the problem-solving approach is clear and easy to follow.
The goal of this walkthrough is to build confidence and familiarity with the methods used in solving various types of problems. Through careful analysis of each example, learners will gain valuable insights into how to tackle similar questions on their own.
Example 1: Solving for Unknown Variables
In this example, we will solve a problem involving unknown variables and linear equations. The steps below guide you through the process of isolating variables and solving the equation.
| Step | Description | Example |
|---|---|---|
| 1 | Identify the equation | x + 5 = 10 |
| 2 | Isolate the variable | x = 10 – 5 |
| 3 | Solve the equation | x = 5 |
Example 2: Applying a Proportionality Equation
This example demonstrates how to apply a proportionality equation to solve a problem involving ratios. The steps guide you through determining the unknown value based on the given proportion.
| Step | Description | Example |
|---|---|---|
| 1 | Set up the proportion | 3/4 = x/12 |
| 2 | Cross-multiply | 3 * 12 = 4 * x |
| 3 | Solve for x | x = 9 |
By breaking down these examples in detail, you can see how each step leads to the correct solution. With practice, you will become more comfortable applying these methods to similar problems on your own.
Tips for Mastering Chapter 6 Topics
Mastering the concepts in this section requires a focused approach and consistent practice. By implementing a few targeted strategies, you can improve both your understanding and your ability to apply the material effectively. This section offers tips to help you gain a deeper grasp of the key topics and enhance your problem-solving skills.
The following strategies focus on breaking down complex ideas into manageable parts, reinforcing your understanding through active practice, and leveraging helpful resources. These tips will guide you toward mastering the material and tackling any challenges with confidence.
Develop a Strong Foundation
Before diving into advanced topics, ensure that you have a solid understanding of the basic concepts. Strengthening your foundational knowledge makes it easier to tackle more difficult problems and apply advanced techniques with ease.
| Tip | Description |
|---|---|
| Review Key Principles | Go over basic concepts regularly to reinforce your understanding. This will make more complex ideas easier to grasp. |
| Identify Common Patterns | Look for patterns in problems to quickly identify similar solutions. Recognizing these patterns reduces the time spent solving similar exercises. |
Practice Consistently
One of the most effective ways to master new topics is through consistent and focused practice. The more problems you solve, the more confident you will become in applying the methods you’ve learned.
| Tip | Description |
|---|---|
| Start with Easy Problems | Begin by solving simpler problems to build confidence. Gradually move on to more challenging ones as you become comfortable with the material. |
| Track Your Progress | Keep a record of your practice sessions to monitor your improvement. Focus on areas where you struggle and revisit them regularly. |
By following these strategies, you will develop a deeper understanding of the topics and improve your ability to apply them effectively. With consistent effort and a strategic approach, mastering the material becomes an achievable goal.
How to Review Chapter 6 Efficiently
Efficient review strategies are key to retaining and applying what you’ve learned. By structuring your review sessions effectively, you can reinforce important concepts, identify areas of weakness, and improve your overall understanding. This section provides practical methods to streamline the review process, ensuring that you make the most of your study time.
The following tips focus on prioritizing critical content, testing your knowledge actively, and revisiting challenging concepts. By implementing these strategies, you can achieve a more thorough understanding in less time.
Prioritize Key Concepts
Not all topics need the same level of attention during review. Focus on the most important concepts and those areas where you may struggle the most. Prioritizing ensures that you spend your time wisely and don’t waste effort on material you’re already comfortable with.
- Identify the core ideas and skills from the section.
- Review examples that highlight how these concepts are applied.
- Skip over material you feel confident in and devote more time to difficult areas.
Test Yourself Regularly
Active recall is one of the best ways to reinforce knowledge. Testing yourself not only helps you gauge your understanding, but it also boosts memory retention. Regular self-assessment ensures that the material stays fresh in your mind and highlights any gaps in your knowledge.
- Complete practice problems without looking at solutions.
- Review your incorrect answers to understand mistakes.
- Use flashcards or quizzes to test your memory on key terms and formulas.
By following these strategies, you can review the material more efficiently, leading to stronger retention and greater mastery of the content. Regular, focused sessions are the key to effective review and long-term success.
Tools and Resources for Better Understanding

To gain a deeper understanding of the material, it’s crucial to leverage a variety of tools and resources that can enhance your learning experience. These resources not only provide additional explanations and examples but also offer interactive ways to engage with the content. Whether you’re a visual learner or someone who benefits from practical exercises, there are tools designed to meet different needs and learning styles.
In this section, we’ll explore several effective resources that can help reinforce your knowledge and improve your problem-solving abilities. These tools will allow you to gain a clearer, more comprehensive grasp of the topics you’re studying.
Online Platforms and Websites
Online platforms can be a great way to access interactive tutorials, problem sets, and detailed explanations. Many websites cater specifically to learners, offering a variety of resources that can make complex topics easier to understand.
- Interactive Tutorials: Websites like Khan Academy and Coursera offer free tutorials that break down difficult concepts in a simplified manner.
- Practice Problems: Platforms like Quizlet and IXL provide problem sets that are designed to help you practice and reinforce your understanding of key concepts.
- Video Lessons: YouTube channels such as CrashCourse or PatrickJMT provide visual explanations that can clarify difficult topics through engaging videos.
Textbooks and Workbooks
While digital resources are incredibly helpful, traditional textbooks and workbooks remain essential tools for understanding material in depth. These printed resources often provide step-by-step solutions, example problems, and exercises that guide you through the learning process.
- Comprehensive Textbooks: Many textbooks offer detailed explanations and examples that can be helpful for students who prefer reading and referencing printed material.
- Workbook Exercises: Workbooks often include exercises and solutions that allow you to practice problem-solving in a structured format.
- Study Guides: Study guides can summarize key points from textbooks, giving you a quick overview of the material and helping you focus on the most important topics.
By combining these resources with regular study sessions and active problem-solving, you’ll be well-equipped to understand the material more thoroughly and confidently tackle any challenges that come your way.
Analyzing Common Student Struggles
When tackling complex subjects, many students face similar challenges that can hinder their progress. These obstacles often arise from misunderstandings, gaps in foundational knowledge, or a lack of effective problem-solving strategies. By recognizing and analyzing these common struggles, students can develop strategies to overcome them and improve their understanding.
This section will explore the most frequent difficulties students encounter and offer insights into how to address them. Identifying these issues early allows learners to focus on strengthening weak areas and refining their approach to problem-solving.
- Difficulty with Abstract Concepts: Many students struggle to grasp abstract ideas, particularly when they are presented without clear, relatable examples. It is important to break these concepts down into smaller, more tangible components to better understand their application.
- Poor Problem-Solving Techniques: Without the proper problem-solving techniques, students can become stuck or overwhelmed when faced with challenging exercises. Developing a step-by-step approach to solving problems can significantly improve outcomes.
- Inconsistent Practice: Infrequent or inconsistent practice is another common issue. Mastery of difficult topics requires regular, focused practice to reinforce learning and ensure concepts are internalized.
- Lack of Confidence: Students who lack confidence in their ability to succeed may hesitate to attempt problems or may give up too soon. Building confidence comes from repeated practice, making mistakes, and learning from them.
By acknowledging and addressing these struggles, students can take proactive steps to enhance their understanding and overcome the barriers that often slow progress. With persistence and the right strategies, any learner can improve and master the material more effectively.
Why Chapter 6 is Crucial for Success
Mastering the material in this section plays a pivotal role in building a strong foundation for subsequent topics. The concepts covered provide essential skills that will be applied in future lessons, making it a critical stepping stone for overall academic success. A firm grasp of the content not only helps in the short term but also ensures long-term understanding and progress in more advanced subjects.
Understanding the key principles discussed here offers students a deeper comprehension of the subject, allowing them to approach more complex problems with confidence and clarity. The strategies and techniques learned will be used repeatedly, creating a solid framework for future learning challenges.
Building Critical Skills

This section introduces fundamental skills that are directly applicable to real-world scenarios. Whether it’s problem-solving, logical reasoning, or analytical thinking, mastering these abilities is essential for both academic performance and personal growth. These skills will continue to be used in more advanced studies, making early mastery particularly important.
Connecting Concepts for Future Learning
In addition to reinforcing essential skills, this section connects various concepts that will be explored in greater depth in later stages. Without a strong understanding of these topics, students may find it difficult to grasp future content. Therefore, dedicating time and effort to thoroughly understand this section is essential for continued success in the subject.
How to Track Progress in Chapter 6
Monitoring progress in this section is crucial for staying on track and ensuring that all key concepts are fully understood. Regularly assessing your understanding allows you to identify areas of strength and weaknesses, helping you focus on areas that require more attention. Tracking progress also boosts motivation and confidence as you see improvement over time.
There are several methods to effectively gauge your progress. Whether through self-assessment, working with peers, or utilizing external resources, consistent evaluation will ensure that you remain on the path toward mastering the material.
Methods to Track Your Understanding
- Practice Tests: Take regular quizzes and practice problems to evaluate your knowledge. This will give you a clear indication of which areas need improvement.
- Review Notes: Regularly go back and review your notes to reinforce key ideas and identify any concepts that are unclear or need further study.
- Set Personal Milestones: Break down the material into manageable sections and set goals for completing them. This allows you to track progress more effectively and stay motivated.
Utilizing External Resources
External resources such as online tutorials, study guides, and peer groups can provide additional support and give you different perspectives on the material. These tools can be particularly helpful for areas that you find difficult, offering alternate explanations or methods to grasp the concepts more thoroughly.
By using these strategies consistently, you can keep track of your progress and ensure that you are ready to move on to more complex topics with confidence.
Additional Practice for Core Connections
To master the material, additional practice is essential. Reinforcing the concepts learned through exercises and problems is one of the most effective ways to solidify your understanding. By tackling a variety of problems, you can ensure that the skills and techniques are deeply ingrained and become second nature. Regular practice not only boosts retention but also builds confidence in applying the knowledge in different contexts.
Here are some additional exercises and resources that can help you further develop your skills. These exercises range from basic to more advanced problems, allowing you to gradually build up your competence. Consistently working through these challenges will give you the practice needed to excel in the subject matter.
| Exercise Type | Description | Difficulty Level |
|---|---|---|
| Basic Practice Problems | Simple questions that test fundamental skills and concepts from the section. | Easy |
| Timed Drills | Problems designed to be completed under time pressure, improving speed and efficiency. | Medium |
| Advanced Application Problems | Complex problems that require you to apply multiple concepts and techniques. | Hard |
| Peer Group Discussions | Collaborating with peers to solve problems and discuss different methods of solving. | Medium |
By regularly engaging with these exercises, you will reinforce the material and prepare yourself for more challenging problems in the future. Remember, the key to success lies in persistent practice and a proactive approach to mastering the content.
Preparing for Chapter 6 Assessments
Preparing for assessments requires more than just reviewing notes. It involves actively engaging with the material, practicing problem-solving techniques, and understanding key concepts thoroughly. Effective preparation also means organizing your study time efficiently, ensuring you cover all essential topics, and identifying areas where you may need additional focus. By building a strong foundation in the subject, you can approach the test with confidence and clarity.
One of the best ways to prepare is to work through various types of problems. These problems should include both those covered in the lessons and those that require you to think critically and apply concepts in different contexts. Regular practice will help you identify any gaps in your knowledge, giving you the opportunity to address them before the assessment.
In addition to solving problems, it’s important to review any past assessments or quizzes to get a sense of the question types and the areas typically emphasized. Reviewing your mistakes from previous tests is also a helpful exercise in preventing similar errors from occurring in future evaluations.
Lastly, remember to incorporate time management into your study routine. Set aside specific time slots for different topics, and ensure you allow for breaks to maintain focus and energy. The goal is to approach your preparation in a systematic and thorough way so you can perform your best when the assessment arrives.