2002 AP Calculus AB Free Response Solutions

Preparing for advanced mathematics exams involves mastering a variety of problem-solving strategies. By carefully analyzing past test items, students can gain valuable insights into the expectations and problem structures. This section focuses on providing a detailed breakdown of key concepts and the steps required to approach complex questions effectively.

Breaking down complex problems into manageable steps is essential for success. The exercises covered in this article highlight critical thinking and application of mathematical principles that are central to achieving high marks. By exploring various problem types, you will build the skills necessary to navigate challenging assessments.

Focused practice plays a key role in refining your approach. Whether tackling derivatives, integrals, or optimization challenges, understanding the core techniques and utilizing the right strategies ensures that you are prepared for any scenario. This guide is designed to offer clarity and structure, helping you improve your performance and confidence during exams.

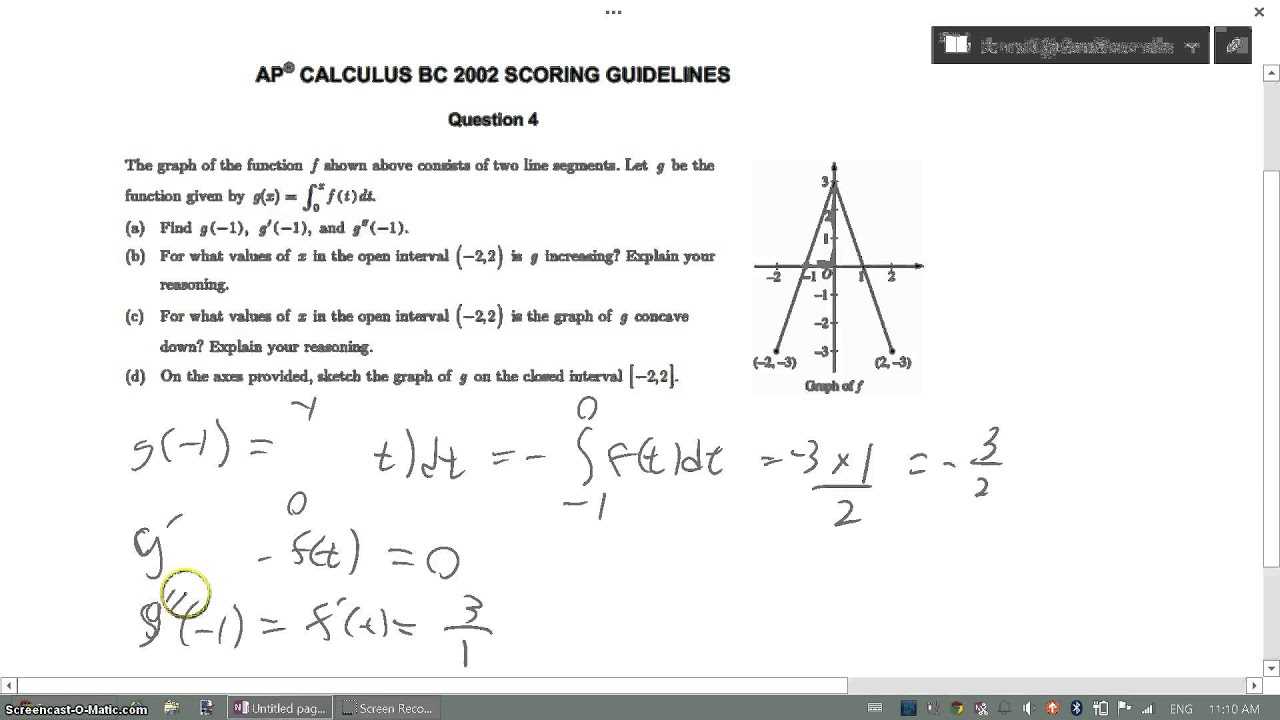
2002 AP Calculus AB Free Response Guide

In this section, we explore key strategies and techniques for solving the more complex questions often seen in mathematics exams. These types of questions test your ability to apply theoretical knowledge to practical scenarios, requiring both analytical and computational skills. Success lies in understanding the core principles and breaking down each problem into smaller, solvable steps.

Important Problem-Solving Techniques

To approach these challenging questions, focus on the following techniques:

• Problem Breakdown: Carefully read through each problem, identifying key information and what is being asked.
• Use of Formulas: Be familiar with the essential formulas and apply them correctly to simplify calculations.
• Logical Reasoning: Develop a clear and structured approach to derive the solution, ensuring each step is based on sound reasoning.

Common Mistakes to Avoid

Even the most experienced students can fall into certain traps. Here are some common mistakes and how to avoid them:

1. Skipping the Steps: Rushing through the problem can lead to overlooked details and mistakes in calculations.
2. Misapplying Concepts: Ensure the correct mathematical techniques are applied to each problem, as errors can arise from using the wrong method.
3. Neglecting Units: Always check if the units of measurement in a word problem align with the expected outcome.

By understanding these strategies and avoiding typical pitfalls, you can improve your chances of mastering the more difficult parts of the exam and earning a higher score. The key to success lies in preparation, practice, and careful attention to detail.

Overview of the 2002 Exam

This section provides a comprehensive look at the structure and format of the mathematics exam that was administered in 2002. The exam is designed to assess a wide range of skills, from basic concepts to more complex problem-solving abilities. The structure typically includes multiple-choice questions and open-ended problems that require detailed solutions.

Structure and Timing of the Exam

The exam is divided into two main sections, each focusing on different aspects of mathematical knowledge. The first section generally consists of multiple-choice questions, while the second section is focused on free-response tasks. Here is a general breakdown of the exam:

Section	Content	Time Limit
Section 1	Multiple-choice questions covering a broad range of topics	1 hour 30 minutes
Section 2	Open-ended problems that test deeper understanding	1 hour 30 minutes

Key Areas Tested

The questions in this exam focus on critical areas of mathematics, requiring students to demonstrate both theoretical understanding and practical application. The exam tests a variety of topics, including:

• Derivatives and their applications
• Integrals and area under curves
• Limits and continuity
• Fundamental theorems of calculus

Understanding the structure and the time constraints of the exam is crucial for success. Preparing efficiently and practicing a wide range of problems will help ensure you can tackle each section with confidence.

Key Topics Covered in Free Response

The open-ended portion of the exam is designed to assess a deeper understanding of mathematical principles and the ability to apply them to real-world scenarios. These problems often require a combination of multiple techniques and critical thinking to solve. Below are the main topics that are commonly covered in this section, highlighting the key areas of focus.

Core Concepts and Techniques

The questions in this section often revolve around the following fundamental concepts:

• Derivatives: Understanding rates of change, optimization, and related rates.
• Integrals: Calculating areas under curves, volumes of solids, and interpreting definite integrals.
• Limits: Analyzing behavior of functions as they approach specific points or infinity.
• Series and Sequences: Working with sequences, series convergence, and approximations.

Application-Based Problems

The open-ended questions often require applying the above concepts to practical situations. These types of problems include:

• Optimization Problems: Finding maximum or minimum values in real-life contexts, such as maximizing profit or minimizing cost.
• Motion Problems: Analyzing the movement of objects, including velocity and acceleration calculations.
• Area and Volume Calculations: Using integration to find areas between curves or volumes of solids of revolution.
• Rate of Change Problems: Solving real-world problems involving rates such as population growth or decay.

Mastering these key areas will significantly improve your ability to tackle the open-ended questions effectively. Focus on practicing a variety of problems to develop a well-rounded understanding of how to apply mathematical principles in different contexts.

Strategies for Tackling Free Response Questions

When approaching complex open-ended questions in mathematics exams, having a clear strategy is essential for success. These problems often require more than just applying formulas–they challenge you to think critically and structure your solution in a logical, step-by-step manner. Developing effective strategies can make a significant difference in how quickly and accurately you solve these problems.

Key Strategies for Success

To maximize your chances of performing well on these types of questions, follow these essential strategies:

• Read Carefully: Begin by thoroughly reading the question to understand what is being asked. Identify key information and the steps you need to take.
• Plan Your Approach: Before diving into calculations, take a moment to outline the steps required to solve the problem. This helps organize your thoughts and ensures a systematic approach.
• Show All Work: Always demonstrate each step in your solution. Even if you arrive at the correct final answer, partial credit may be awarded for showing your reasoning.
• Check Units and Interpretations: Pay close attention to the units in word problems and ensure your answer makes sense in the context provided.
• Time Management: Allocate your time wisely. Don’t spend too much time on one problem if you’re stuck–move on and return later if needed.

Common Pitfalls to Avoid

While it’s important to follow strategies, it’s equally crucial to avoid common mistakes that can hinder your performance:

Mistake	How to Avoid It
Skipping Steps	Always write out intermediate steps to ensure accuracy and make it easier to identify mistakes.
Incorrect Application of Formulas	Review your formulas before using them to make sure they apply to the specific problem you’re solving.
Rushing Through Problems	Take the time to check your answers and ensure all parts of the question have been addressed.

By employing these strategies and being mindful of common mistakes, you can approach each problem with greater confidence and accuracy, maximizing your performance on the exam.

Important Formulas for AP Calculus AB

In order to solve complex problems efficiently in advanced mathematics exams, having a strong grasp of essential formulas is crucial. These formulas serve as the foundation for a wide range of problem types, from derivatives and integrals to optimization and motion. Knowing when and how to apply them will greatly enhance your problem-solving abilities and speed during the exam.

Core Derivatives and Integrals

The following formulas are fundamental for understanding rates of change, areas under curves, and many other key concepts:

• Power Rule: d/dx [x^n] = n * x^(n-1)
• Product Rule: d/dx [f(x) * g(x)] = f'(x) * g(x) + f(x) * g'(x)
• Quotient Rule: d/dx [f(x) / g(x)] = (f'(x) * g(x) – f(x) * g'(x)) / (g(x))^2
• Chain Rule: d/dx [f(g(x))] = f'(g(x)) * g'(x)
• Definite Integral (Area under a curve): ∫ [a, b] f(x) dx = F(b) – F(a)

Advanced Techniques and Applications

In addition to basic derivatives and integrals, the following formulas are vital for tackling more advanced problems, such as those involving motion, optimization, and rates of change:

• Mean Value Theorem: f'(c) = (f(b) – f(a)) / (b – a) for some c in [a, b]
• Fundamental Theorem of Calculus: ∫ [a, b] f(x) dx = F(b) – F(a) (where F'(x) = f(x))
• Related Rates: dx/dt, dy/dt, dz/dt (solve for the rate of change of one quantity in terms of another)
• Optimization: Use critical points and the second derivative test to find maximum and minimum values.

Familiarity with these formulas allows you to approach problems with confidence and clarity, ensuring that you can efficiently tackle the wide range of questions typically found in advanced exams.

Common Mistakes in Free Response Answers

When tackling open-ended mathematical problems, students often encounter certain pitfalls that can impact their overall performance. These mistakes can arise from misunderstandings of the concepts, misapplication of formulas, or simple oversights during the problem-solving process. Identifying and avoiding these common errors is crucial for improving both accuracy and efficiency in solving complex tasks.

Frequent Errors to Watch For

Below are some of the most common mistakes that students make when addressing complex mathematical problems:

• Skipping Steps: Failing to show intermediate steps can lead to loss of partial credit, even if the final answer is correct.
• Incorrect Application of Formulas: Using the wrong formula or applying a formula incorrectly can drastically change the outcome of the solution.
• Misinterpreting the Problem: Misunderstanding the wording of a question can lead to solving for the wrong quantity or applying the wrong technique.
• Not Checking for Units: Ignoring units or mismatching them in word problems can result in incorrect answers and a lack of clarity in the solution.
• Rushing: Many mistakes are made due to time pressure, such as missing negative signs or miscalculating a simple arithmetic operation.

How to Avoid These Mistakes

By being aware of these common pitfalls, you can take steps to minimize errors during problem-solving. Here are a few tips to help you stay on track:

Mistake	How to Avoid It
Skipping Steps	Write out every intermediate step, even if you think it’s obvious. This ensures clarity and may earn partial credit.
Incorrect Application of Formulas	Double-check the formulas you’re using and ensure they are appropriate for the specific problem you’re solving.
Misinterpreting the Problem	Carefully read the problem twice before starting. Identify what the problem is asking for and note any key information provided.
Not Checking for Units	Always check units at each step, especially in word problems, and ensure consistency in the final result.
Rushing	Manage your time carefully. If you’re stuck on one part, move on and return to it after completing the rest of the exam.

By avoiding these common mistakes, you can significantly improve your performance on open-ended questions and increase your chances of achieving the best possible score.

Step-by-Step Solution Breakdown

Solving complex mathematical problems often requires a methodical approach. Breaking down a solution into manageable steps not only helps ensure accuracy but also allows for a clear demonstration of the reasoning behind each stage of the problem. This approach makes it easier to spot mistakes and ensures that the problem is fully addressed.

Understanding the Problem

The first step in solving any problem is understanding the question and identifying the given information. Carefully read the prompt, noting the important data and what needs to be solved. Ask yourself the following:

• What are the known values?
• What is being asked for?
• Are there any specific conditions or constraints in the problem?

Once you have a clear understanding of the problem, you can begin formulating a plan of action. This plan will help you determine the best approach for tackling the problem and applying the right formulas or techniques.

Step-by-Step Breakdown

Next, follow these steps to break down the solution:

• Step 1: Setup the Equation – Use the information from the problem to set up the appropriate equation or expression. Ensure that all variables are defined and represented correctly.
• Step 2: Apply Mathematical Techniques – Use the necessary mathematical tools, such as differentiation, integration, or other relevant methods, to manipulate the equation and move towards the solution.
• Step 3: Solve the Equation – Simplify the equation and solve for the unknown variable. Be sure to check for any possible errors or overlooked details during this process.
• Step 4: Interpret the Solution – Once you have a solution, interpret it in the context of the problem. Make sure your answer makes sense and matches the units and conditions given.
• Step 5: Verify and Double-Check – Finally, review your entire solution to confirm that all steps were followed correctly and that the solution is accurate.

By following a structured, step-by-step breakdown, you can approach even the most challenging problems with confidence and clarity, ensuring that no part of the problem is overlooked.

Understanding the Grading Rubric

When tackling open-ended mathematical questions, understanding the grading criteria is essential to maximize your score. The grading rubric outlines how each part of your solution will be evaluated, breaking down the key components that examiners are looking for. By familiarizing yourself with these guidelines, you can ensure that your responses meet all the necessary requirements and earn the maximum possible points.

The grading system typically focuses on several key aspects of your response, including clarity, accuracy, and the logical progression of your solution. Each part of the problem may be weighted differently, depending on the complexity and importance of the task at hand. It’s crucial to provide thorough explanations, demonstrate the application of the correct methods, and present your work in a clear and organized manner.

Additionally, many rubrics award points for partial credit, meaning that even if your final solution is incorrect, you may still receive points for demonstrating correct approaches or intermediate steps. This makes it even more important to show your work and break down each stage of the process clearly.

Ultimately, understanding the grading rubric helps you prioritize what is most important in each question. By focusing on demonstrating your understanding of the material and providing clear, well-structured solutions, you can improve your chances of achieving a higher score on open-ended tasks.

Approaching Limits and Derivatives

In mathematics, understanding the concept of approaching values and the rate of change is fundamental for solving many types of problems. Limits and derivatives play a crucial role in analyzing functions and understanding their behavior at specific points. These concepts allow us to describe how functions behave as they approach certain values and how they change over time or space.

Limits are essential for understanding the behavior of functions at points where they may not be directly defined or where they exhibit unusual characteristics, such as asymptotes or discontinuities. By evaluating limits, you can determine the value a function approaches as the input gets infinitely close to a specific point.

Derivatives, on the other hand, represent the instantaneous rate of change of a function. They help us understand how a function’s output changes relative to its input, making derivatives crucial for problems involving motion, optimization, and rates of change. By calculating derivatives, you can find the slope of the tangent line at any given point on the graph of a function.

When approaching problems involving these concepts, it’s important to systematically apply the rules and techniques associated with limits and derivatives. This includes using algebraic manipulation, applying known limit laws, and differentiating using standard rules. Mastery of these methods allows for a deeper understanding of the underlying behavior of functions and provides the tools necessary to solve complex mathematical problems.

Using Integration in Free Response Problems

In many complex problems, the ability to calculate areas, volumes, and other quantities based on continuous functions is essential. Integration is a powerful tool for solving such problems, allowing you to find the cumulative effect of a rate of change over a given interval. By applying integration techniques, you can solve problems that involve finding areas under curves, calculating accumulated quantities, and more.

Understanding the Problem and Setup

When using integration in response to mathematical problems, the first step is always to understand the context and set up the correct integral. Carefully read the problem to identify the function or rate of change that needs to be integrated and the interval over which integration should occur. Pay close attention to units, limits, and any additional information given in the prompt, as these will guide you in setting up the proper equation.

Common Techniques for Integration

Depending on the structure of the problem, various integration methods may be required. Some of the most commonly used techniques include:

• Definite Integration: Used to calculate the accumulated value over a specific interval, such as the area under a curve between two points.
• Indefinite Integration: Used to find the general antiderivative of a function, often leading to the general solution of a differential equation.
• Integration by Parts: A method used when the integrand is a product of two functions, facilitating the integration of more complex expressions.
• Substitution: A technique used to simplify integrals by making a substitution that transforms the problem into a more manageable form.

Steps for Effective Integration

When applying integration to solve a problem, follow these steps:

1. Identify the integrand: Determine the function that needs to be integrated.
2. Set the limits: If the problem is asking for a specific area or quantity, make sure to identify the correct limits for the integral.
3. Choose the method: Based on the form of the integrand, select the appropriate method (substitution, integration by parts, etc.).
4. Carry out the integration: Perform the integration and simplify the result.
5. Interpret the result: Ensure that the final answer makes sense in the context of the problem and matches the required units or conditions.

By mastering integration techniques and carefully following these steps, you can solve a wide range of problems involving continuous change and accumulation.

How to Handle Word Problems Effectively

Word problems often present a challenge, as they require the translation of real-world scenarios into mathematical equations and models. Effectively solving these problems involves understanding the context, identifying the key elements, and applying the appropriate mathematical methods. With the right approach, you can break down complex problems into manageable steps.

To handle word problems effectively, it’s crucial to follow a structured approach. Start by carefully reading the problem and extracting the important information. Once you’ve identified the key details, decide which mathematical concepts or operations are required to solve the problem. Keep in mind that organizing the information and making connections between the real-world context and mathematical principles is essential for success.

Steps for Solving Word Problems

Here are some key steps to follow when working through word problems:

1. Read the Problem Carefully: Understand the situation fully before attempting to solve it. Pay attention to specific terms and quantities mentioned in the problem.
2. Identify Key Information: Extract relevant data, such as given numbers, variables, or relationships between quantities.
3. Define Variables: Assign variables to unknown quantities and ensure they represent the correct real-world elements.
4. Translate into Mathematical Language: Convert the word problem into equations, inequalities, or other mathematical forms that capture the relationships between the variables.
5. Apply the Appropriate Techniques: Use appropriate methods, such as algebraic manipulation, geometry, or optimization, depending on the problem’s nature.
6. Check Your Work: After solving the problem, revisit the solution to ensure it makes sense in the context of the original scenario. Verify the calculations and confirm that the units match.

Tips for Success

• Draw Diagrams: Visualizing the problem can often make complex scenarios easier to understand, especially in geometry or rate-related problems.
• Break the Problem Down: If the problem involves multiple steps or stages, break it down into smaller parts and solve them one at a time.
• Look for Patterns: Word problems often follow certain patterns or structures. Recognizing these can speed up the problem-solving process.
• Practice Regularly: The more word problems you solve, the better you will get at identifying the key steps and applying the correct techniques.

By following these steps and using these strategies, you can tackle word problems with confidence and accuracy, improving your problem-solving skills over time.

Exploring Techniques for Related Rates

When multiple quantities change over time, it becomes essential to understand how these changes are connected. In many real-world scenarios, such as the movement of objects or the growth of physical shapes, the rates at which variables change are interdependent. Solving these problems involves understanding the relationships between the changing quantities and using mathematical techniques to find the rates of change for each variable.

To approach these problems effectively, it’s important to apply the principles of differentiation to uncover how one variable influences another. By understanding how different quantities relate and how they evolve with time, it becomes possible to calculate the rate at which one is changing, given the changes in other variables.

Key Steps in Solving Related Rates Problems

Follow these essential steps to tackle related rates problems:

1. Identify the Variables: Determine the quantities that change over time and note what is given and what needs to be found.
2. Establish a Relationship: Set up an equation that connects the changing variables. This could come from geometry, physics, or other principles specific to the problem at hand.
3. Draw a Diagram: If applicable, sketch a diagram to better understand the situation. A visual representation helps clarify the relationships between the quantities and their rates of change.
4. Differentiate the Equation: Use implicit differentiation to differentiate the equation with respect to time, making sure to account for all variables that change.
5. Substitute Known Values: Insert the known values into the differentiated equation to solve for the unknown rate of change.
6. Verify Units and Solution: Check that your units are consistent, and verify that your final answer makes sense within the context of the problem.

Common Applications of Related Rates

• Expanding and Shrinking Volumes: Problems involving objects such as balloons or tanks, where the volume is changing based on the changing size or height of the object.
• Motion Problems: These deal with the rates of change of position, velocity, or acceleration of moving objects, where one rate influences the others.
• Changing Geometrical Properties: Problems related to changing dimensions of geometric shapes (like spheres or cones), where rates of change are tied to surface area or volume.
• Fluid Dynamics: Situations where the rate of change of fluid in containers, like water flowing out of a tank, is examined.

Mastering the techniques for solving related rates problems allows for a deeper understanding of how variables are interlinked and provides a powerful method for solving dynamic, time-dependent problems.

Optimization Problems in AP Calculus AB

Optimization problems are essential in mathematics, especially when it comes to finding the best possible solutions under given conditions. These types of problems involve maximizing or minimizing a specific quantity, such as cost, area, volume, or profit. In many real-life scenarios, optimization is used to find the most efficient outcome, whether it’s minimizing resources or maximizing results. Solving these problems typically involves identifying key variables, setting up equations, and applying differentiation to determine the critical points where optimal values occur.

The process for solving optimization problems involves a few important steps. First, it’s crucial to understand the problem and define the variables clearly. Then, an objective function is created that expresses the quantity to be optimized. After the function is set up, differentiation is used to find critical points, which are potential solutions where the function might achieve a maximum or minimum value. These points are then tested to determine which one provides the optimal result. In addition, constraints and boundaries often play a critical role in solving these problems effectively.

Steps for Solving Optimization Problems

The general approach to solving optimization problems can be broken down into the following steps:

1. Understand the problem: Read through the problem carefully to determine what needs to be maximized or minimized, and identify the variables involved.
2. Define variables: Assign variables to the unknown quantities, such as dimensions, cost, or time, to establish a clear representation of the problem.
3. Set up an objective function: Express the quantity to be optimized in terms of the variables. This function will be the basis for finding the maximum or minimum values.
4. Identify constraints: Recognize any relationships or limits that restrict the variables. These constraints help reduce the complexity of the problem.
5. Differentiate the objective function: Take the derivative of the function with respect to the variables to find the critical points.
6. Analyze critical points: Solve for the values of the variables that make the derivative equal to zero, and use the second derivative test or other methods to determine whether these points correspond to a maximum, minimum, or inflection point.
7. Verify the solution: Double-check the solution to ensure it satisfies all constraints and makes sense in the context of the problem.

Applications of Optimization in Real-World Scenarios

Optimization techniques are used across a wide range of fields. Here are some examples of where optimization problems arise:

• Designing Maximum Area Enclosures: Given a fixed perimeter, determining the dimensions of a rectangular fence that maximize the enclosed area.
• Minimizing Cost: Finding the most cost-effective way to produce a set number of units while keeping production costs as low as possible.
• Maximizing Profit: In business, optimizing the pricing of products or the allocation of resources to maximize revenue and profit margins.
• Maximizing Volume: Problems like designing a container with a specific amou
  

  Examining Areas and Volumes in Calculus

  In mathematics, one of the most fundamental concepts involves determining the size or extent of objects, whether that means calculating the area of a flat surface or the volume of a three-dimensional shape. These calculations are essential not only in theoretical mathematics but also in fields such as physics, engineering, and economics. By using methods such as integration, one can precisely measure areas under curves or volumes of solids, even when the boundaries are irregular or complex.

  Understanding how to compute areas and volumes begins with the concept of limits and sums. For areas, the process often involves finding the accumulation of values over a certain interval. In the case of volumes, the goal is to understand how the shape of an object changes along its axis and how this change contributes to its overall size. These calculations are usually achieved by breaking down the problem into simpler, manageable sections, integrating over the region of interest, and then summing the results.

  Methods for Finding Areas

  To find the area of a region between curves or under a curve, integration is commonly used. The general approach includes the following steps:

  1. Set the limits of integration: Identify the points at which the region starts and ends along the x-axis (or y-axis, depending on the orientation).
  2. Choose the appropriate function: Define the function that describes the boundary of the region whose area you want to find.
  3. Integrate the function: Use the integral to calculate the total area between the curve and the x-axis (or y-axis) over the specified limits.
  4. Subtract areas if needed: In cases where there are multiple curves, subtract the areas under the unwanted curves from the total area to get the desired result.

  Techniques for Calculating Volumes

  

  Similar to area calculations, volume calculations often involve breaking down complex shapes into simpler components and summing them using integration. Common techniques include:

  • Disk Method: Used to find the volume of a solid of revolution when the region is rotated around an axis. The volume is computed by integrating the area of circular disks formed at each point along the axis of rotation.
  • Washer Method: Used when there is a hole in the center of the solid. The volume is computed by subtracting the volume of the inner radius from the outer radius at each point.
  • Cylindrical Shells: This method involves wrapping a cylindrical shell around the axis and integrating the surface area of the shell to determine the volume.

  By employing these techniques, complex shapes can be analyzed and their sizes determined, providing critical insights into both theoretical and applied mathematical problems.

  Tips for Time Management During the Exam

  Effective time management during an exam is key to ensuring that all questions are answered thoroughly without feeling rushed. With limited time and a range of questions to address, it is crucial to approach the test with a strategy that allows you to allocate your time efficiently. By organizing your efforts and staying focused, you can maximize your performance on each section of the exam.

  Planning Your Time

  The first step in managing your time effectively is to understand how much time you have for the entire exam and break it down into smaller sections based on the number of questions. Consider the following guidelines:

  • Read through the entire exam: Before you start working, take a few minutes to skim through all the questions. This will give you an idea of what to expect and help you prioritize the more time-consuming sections.
  • Allocate time for each section: Estimate how much time you will spend on each question or section. If some questions are worth more points, allocate more time to them. Stick to your planned time limits to avoid spending too much time on any one question.
  • Start with easier questions: Begin with the questions that you feel most confident about. This will help you gain momentum and boost your confidence as you move on to the more challenging problems.

  Staying Focused and Efficient

  During the exam, it’s important to remain calm and efficient. Here are some additional tips to help you stay on track:

  • Avoid perfectionism: While accuracy is important, don’t get stuck trying to perfect one question. If you get stuck, move on and come back to it later if time allows.
  • Use a clock: Keep an eye on the time as you work, but don’t obsess over it. Set specific milestones for yourself to ensure that you are progressing through the exam at an appropriate pace.
  • Leave time for review: Aim to finish your last question with enough time left to review your answers. Check for any mistakes, particularly in complex calculations, and ensure that all questions have been answered.

  By approaching the exam with a clear plan and maintaining focus, you can effectively manage your time and improve your chances of success. Remember, a steady pace and confidence are key to tackling each section efficiently.

  Reviewing the Calculator Policy for AP Exams

  Understanding the rules surrounding the use of calculators during exams is crucial for success. While these devices can provide essential assistance for complex calculations, there are specific guidelines about when and how they can be used. Being familiar with the calculator policy will help ensure that you are fully prepared to follow the exam’s requirements and avoid any potential issues during test day.

  Permitted and Prohibited Calculators

  Not all calculators are allowed in every exam scenario. It’s important to know the types of calculators that are permitted and the ones that are not acceptable. Here are some key points to keep in mind:

  • Permitted models: Most scientific and graphing calculators are allowed, but certain advanced models with additional capabilities may be prohibited.
  • Prohibited calculators: Calculators with internet access, built-in symbolic algebra systems (CAS), or those capable of storing or transmitting information (e.g., smartphones or devices with communication features) are typically not allowed.
  • Calculator use on specific sections: Some parts of the exam may restrict the use of calculators, so be sure to understand which sections allow or prohibit their use.

  Best Practices for Using Calculators

  When using a calculator during the exam, it’s important to follow these best practices to make the most of the device while adhering to the rules:

  • Prepare ahead: Ensure that your calculator is working properly before the exam. Check the batteries and make sure there are no stored notes or previous work that could raise concerns.
  • Know the functions: Familiarize yourself with the features of your calculator, including how to perform key functions like graphing, solving equations, and calculating derivatives or integrals.
  • Use the calculator strategically: While a calculator can speed up calculations, don’t rely on it for every step. It’s important to understand the underlying principles to ensure that you can check your work effectively.

  By reviewing the calculator policy and preparing accordingly, you can avoid any distractions or disqualifications related to device usage and focus your efforts on answering the exam questions with confidence.

  Resources for Further Practice and Study

  To enhance your skills and understanding, it is crucial to explore a variety of study materials that offer diverse ways to practice and review key concepts. The more exposure you get to different types of problems and explanations, the better prepared you will be. Below are several excellent resources to support your continued learning and to provide additional opportunities for practice.

  Online Learning Platforms

  Numerous websites and online platforms offer interactive lessons, practice exercises, and video tutorials. These platforms allow you to work at your own pace and focus on areas where you need improvement:

  • Khan Academy: A comprehensive resource with instructional videos, exercises, and quizzes across various mathematical topics, ideal for reinforcing foundational knowledge and exploring more advanced material.
  • Coursera: Offers online courses created by universities and institutions, complete with video lectures, assignments, and discussions on mathematical principles.
  • Wolfram Alpha: An advanced computational tool that helps solve complex mathematical problems, providing step-by-step solutions and explanations.
  • Brilliant: A platform designed to develop problem-solving and critical thinking skills through interactive lessons and quizzes, covering a range of topics in mathematics and science.

  Books and Study Guides

  Books remain a great tool for structured study, providing detailed explanations, examples, and practice exercises. Several publications are designed specifically to help students prepare for exams and strengthen their understanding:

  • “Practice Problems for Mastery” by James Walters: A collection of problem sets organized by difficulty, with detailed solutions to help improve problem-solving skills.
  • “Advanced Problem Solving” by Michael Thompson: A step-by-step guide to solving complex problems with strategies and tips for success in exams.
  • “Mastering the Concepts” by Barron’s: A well-known study guide that offers practice exams, solutions, and key concepts for review, suitable for both beginning and advanced learners.

  Mobile Apps and Tools

  Mobile apps offer a convenient way to practice on the go. Whether you need quick help or want to test your knowledge while waiting for your next class, these apps can be a valuable addition to your study routine:

  • Photomath: A popular app that allows you to scan math problems and provides detailed, step-by-step solutions to help you understand the process.
  • Desmos Graphing Calculator: A powerful, user-friendly graphing tool that lets you explore functions, plot graphs, and visualize mathematical concepts.
  • Quizlet: An app for creating flashcards and quizzes, helping you memorize important formulas, concepts, and definitions.

  By utilizing these resources, you can improve your understanding, master complex concepts, and build the confidence needed to excel. Whether you prefer interactive online tools, self-paced books, or convenient mobile apps, there are numerous options to fit your study style and goals.