
Success in high-level mathematics assessments depends heavily on the ability to solve complex, multi-step problems under timed conditions. Understanding how to approach these challenges is key to performing well. The problems require a combination of theoretical knowledge and practical problem-solving skills, often involving intricate calculations and logical reasoning.
Preparation for such tests involves not only reviewing key concepts but also practicing effective strategies for tackling different types of questions. Whether you’re working with functions, optimization problems, or real-world scenarios, developing a systematic approach will help you navigate the toughest sections with confidence.
Through targeted practice and careful review of previous tests, students can improve their speed and accuracy. Focusing on techniques that emphasize clarity in thought and precision in calculation will give you the edge needed for optimal performance. Building familiarity with the structure of the tasks and knowing how to manage your time efficiently are critical for achieving the best results.
AP Calculus AB 2025 Free Response Overview
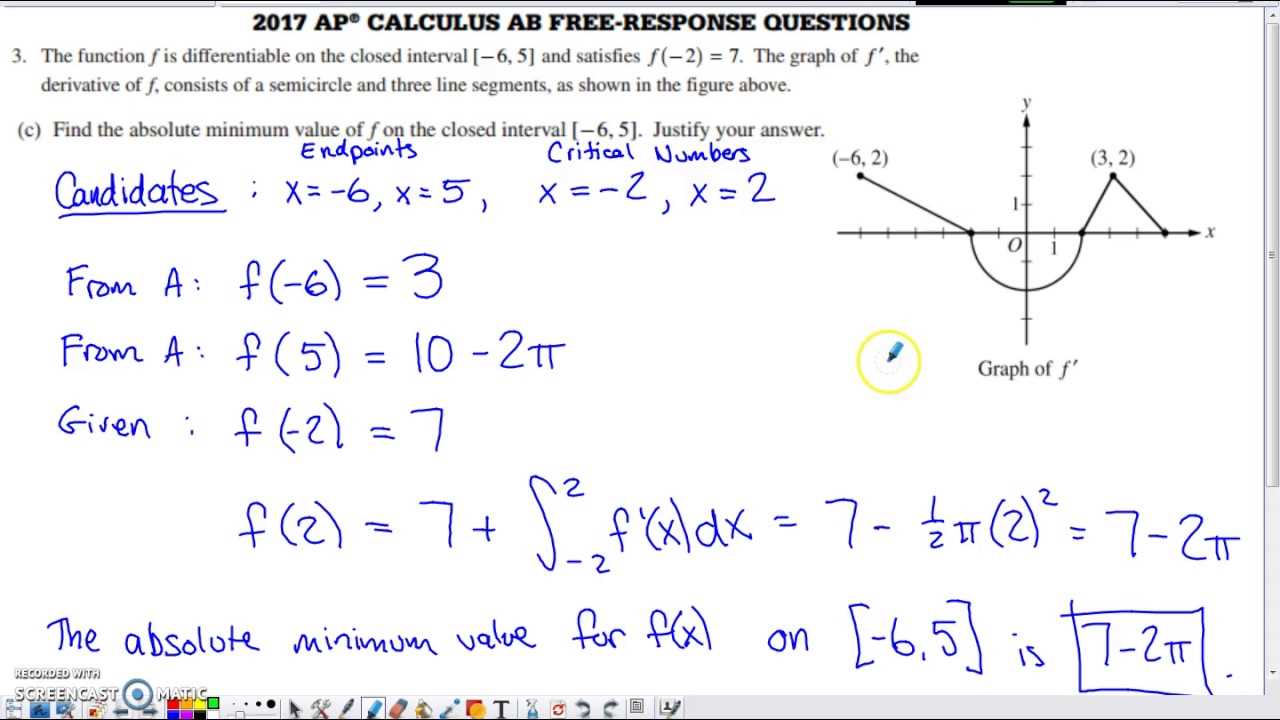
The problem-solving section of the assessment requires students to apply their mathematical knowledge to a series of complex scenarios. These tasks are designed to test both conceptual understanding and the ability to execute calculations in a structured manner. Success depends on presenting clear, logical solutions to a variety of questions that range from theoretical applications to real-world contexts.
Key Characteristics of the Problems
The problems are typically multi-step and demand a thorough approach. Students are expected to not only find the correct results but also demonstrate their understanding through well-organized solutions. Each question is an opportunity to showcase critical thinking and mastery of key principles.
Approach and Strategy
Effective time management and a structured problem-solving strategy are essential for this section. By breaking down each task into smaller, manageable parts and addressing each step methodically, students can increase their chances of success. It is important to remain focused on the core concepts and avoid unnecessary complexity in explanations.
Understanding the Free Response Format
The structured problem-solving section is designed to challenge your ability to think critically and apply mathematical concepts in various contexts. Unlike multiple-choice questions, these tasks require detailed explanations and step-by-step solutions. The focus is on both accuracy and clarity, ensuring that each part of your reasoning is fully expressed and justified.
Each question typically consists of multiple parts, requiring students to perform a series of calculations, explain their reasoning, and often interpret the results. While solving these problems, it is essential to maintain logical progression and avoid skipping steps, as partial credit is awarded based on the work shown. A methodical approach will help you tackle each problem effectively and increase your chances of achieving high scores.
Key Topics for the 2025 Exam
To perform well on this assessment, it is crucial to familiarize yourself with the core subjects that will be tested. These topics require a deep understanding and the ability to apply mathematical principles to a range of problems. Focusing your study efforts on the most significant areas will help you navigate the challenges with confidence and precision.
Functions and Their Properties
Understanding different types of functions and their behaviors is essential for tackling a variety of questions. Whether dealing with polynomial, trigonometric, or exponential functions, students must be able to manipulate equations, analyze graphs, and solve related problems efficiently.
Derivatives and Integrals

Derivatives and integrals form the foundation of many questions in this section. Mastery of differentiation and integration techniques, along with their applications, is crucial for solving complex problems that involve rates of change and areas under curves. Being able to apply these concepts to real-world scenarios will enhance your ability to achieve high marks.
How to Approach Free Response Questions
Approaching complex problem-solving tasks requires a strategic mindset and a clear plan of action. The goal is to break down each question into manageable steps, ensuring that every part is addressed in a logical and organized manner. Instead of rushing through the problems, take the time to think critically and outline your approach before diving into the calculations.
Read the Question Carefully
Start by reading the entire question thoroughly to understand what is being asked. Pay close attention to any specific instructions, as these may guide you toward the correct method of solving the problem. Identifying key terms and what the problem is truly asking for can save valuable time later on.
Organize Your Work

Once you understand the task, organize your work step by step. Begin by outlining the known information, followed by what needs to be determined. This structured approach ensures that you do not skip critical steps and helps you maintain clarity in your reasoning. Always show your work, as partial credit is awarded based on the process, not just the final answer.
Tips for Maximizing Your Score
To achieve the highest possible score, it’s essential to employ strategies that maximize both your accuracy and efficiency. Focusing on key aspects of problem-solving, time management, and presentation will set you up for success. Here are some practical tips to help you optimize your performance during the test:
- Understand the Grading Criteria: Familiarize yourself with the grading rubric to know what is expected in your solutions. Focus on showing clear, logical steps rather than just arriving at the correct answer.
- Manage Your Time Effectively: Allocate a specific amount of time for each question and stick to it. Avoid spending too much time on one question at the expense of others.
- Use Efficient Problem-Solving Techniques: Prioritize strategies that minimize complex calculations. Look for patterns or shortcuts that simplify the process while maintaining accuracy.
- Double-Check Your Work: If time permits, review your solutions to ensure there are no simple mistakes. Checking your work can help catch minor errors that may have been overlooked initially.
- Provide Clear Explanations: Even if you find the solution quickly, make sure to clearly explain your reasoning. A well-written solution demonstrates your understanding and improves your chances of receiving full credit.
By following these strategies, you’ll be able to tackle the most challenging problems with confidence and make the most of your time on test day.
Time Management During the Exam
Efficient use of time is critical when tackling complex tasks under pressure. Without a clear strategy, it’s easy to spend too much time on a single problem and risk running out of time for others. By learning how to pace yourself and allocate appropriate amounts of time to each section, you can improve your chances of completing the test successfully.
Set Time Limits for each problem based on its difficulty. If a task seems particularly time-consuming, move on to the next one and return to it later. This ensures that you’re not caught up in one question for too long, leaving insufficient time for others.
Monitor Your Progress throughout the assessment. Periodically check the clock to ensure you’re staying on track. Being aware of the time helps you make adjustments when needed and prevents last-minute rushing.
Prioritize Tasks by quickly assessing which questions are easier and can be solved faster. Start with these to build momentum, then return to the more challenging ones once you’ve established a time buffer.
Stay Calm and Focused even when the clock is ticking down. A calm and focused mind will allow you to think more clearly and make fewer errors, which ultimately saves time in the long run.
Common Mistakes to Avoid
When tackling challenging tasks, even small mistakes can have a significant impact on your final score. Understanding the common pitfalls that students often fall into can help you avoid these errors and improve your performance. Here are some frequent mistakes to watch out for:
| Mistake | Explanation | How to Avoid It |
|---|---|---|
| Skipping Steps | Many students attempt to solve problems quickly by skipping intermediate steps, which can lead to errors. | Always show your work clearly, even if the steps seem simple. |
| Misinterpreting the Question | It’s easy to misread questions, especially when under time pressure. This can lead to solving a different problem than what was asked. | Carefully read each question multiple times before starting your solution. |
| Forgetting Units or Labels | Forgetting to include units or labels in your final answer can result in losing points, even if the math is correct. | Always include proper units and labels when appropriate. |
| Overcomplicating the Solution | Trying to make the solution more complex than necessary can lead to confusion and mistakes. | Simplify your approach and use straightforward methods where possible. |
| Neglecting to Check Work | Many students rush through the final steps and don’t take the time to review their answers. | Use any remaining time to double-check your calculations and ensure your solutions are correct. |
Practice Problems for Free Response
To build confidence and improve problem-solving skills, it’s essential to practice with a variety of tasks that challenge different aspects of mathematical understanding. Working through practice problems helps familiarize you with the format, increases your speed, and reinforces the key concepts that are frequently tested. The more problems you solve, the more prepared you will be for the real assessment.
Problem 1: Rates of Change
Consider a function f(x) that describes the position of an object at time x. Given the velocity function v(t) = 3t^2 – 2t + 4, determine the acceleration at t = 5. Show all your work.
Problem 2: Area Under a Curve
Find the area between the curve y = x^3 – 4x + 3 and the x-axis over the interval [1, 4]. Include all steps in your solution.
By working through these and similar practice problems, you will improve your ability to approach complex questions methodically, ensuring you understand the underlying principles and can apply them efficiently during the actual test.
Analyzing Past Exam Questions
One of the most effective ways to prepare for a challenging test is by reviewing questions from previous years. By analyzing past problems, you gain insight into the patterns of questioning, the types of concepts that are frequently tested, and the level of complexity you can expect. This approach not only helps you understand what to focus on but also allows you to familiarize yourself with the format and structure of the tasks.
Identifying Key Concepts
Start by looking for recurring themes and topics across different years. This could include specific functions, types of problems, or mathematical concepts that are frequently tested. By recognizing these patterns, you can prioritize your study time on areas that are most likely to appear in the future.
Understanding Solution Strategies

While reviewing past questions, pay close attention to the methods used to solve the problems. Identify the step-by-step strategies that lead to a correct solution and practice these techniques. This not only helps with faster problem-solving but also ensures that your approach aligns with the grading criteria.
Scoring Rubric and Grading Insights
Understanding how your work will be evaluated is crucial for success. The grading system for mathematical assessments typically includes a detailed rubric that outlines how points are awarded based on the accuracy, completeness, and clarity of your solutions. Knowing the specific criteria can help you focus on what matters most during the task and improve your chances of earning full credit.
The rubric typically emphasizes the following key elements:
- Correctness of Solution – Ensure that your final answer is mathematically accurate and corresponds to the requirements of the question.
- Logical Process – Demonstrating a clear and organized approach to solving the problem is essential. Even if the final answer is wrong, a well-documented process can still earn partial credit.
- Clear and Concise Work – Show your work step by step, without skipping important steps. This helps graders follow your reasoning and award points for correct intermediate steps.
- Units and Notations – Properly labeling your answers with the correct units, symbols, and notations can make a significant difference in your score.
By familiarizing yourself with the rubric, you can better tailor your responses to meet the expectations of the graders, which ultimately leads to higher scores.
Essential Strategies for Problem Solving
Effective problem-solving in mathematics requires more than just knowledge of formulas and concepts. It involves a structured approach to break down complex questions into manageable parts and applying logical steps to reach the correct solution. By mastering proven strategies, you can navigate even the most challenging problems with confidence and efficiency.
Key Problem-Solving Techniques
Here are some essential strategies that can enhance your problem-solving ability:
| Strategy | Description | When to Use |
|---|---|---|
| Understand the Problem | Before starting, make sure you clearly understand what is being asked. Take time to identify key information and any constraints. | Always – ensures you focus on the right parts of the problem. |
| Break It Down | Divide complex problems into smaller, more manageable pieces. Solve each step individually before combining the results. | When dealing with multi-step or challenging problems. |
| Use Visual Aids | Draw diagrams, graphs, or tables to better understand relationships and to organize information visually. | When the problem involves geometric or graphical interpretation. |
| Check for Reasonableness | After reaching a solution, assess whether the result makes sense given the context of the problem. | To verify that your solution is correct before finalizing it. |
Mastering these Techniques
Practicing these strategies regularly will not only improve your problem-solving skills but also help you approach each task with a clear, methodical mindset. With consistent application, you’ll become more efficient and effective in finding solutions, no matter the complexity of the question.
How to Use Calculators Effectively
In many mathematical tasks, a calculator can be a valuable tool to simplify complex calculations and speed up problem-solving. However, using it effectively requires understanding when and how to employ its functions. Over-reliance on a calculator without knowing the underlying concepts can lead to mistakes, so it is important to strike a balance between manual problem-solving and using the device for efficiency.
Here are some tips for using calculators effectively during mathematical tasks:
- Know the Functions – Familiarize yourself with your calculator’s features, including its ability to solve equations, graph functions, and calculate derivatives or integrals. Understanding its capabilities will allow you to use it at the right moments.
- Use for Verification – While it’s important to understand the methods behind the solutions, calculators are excellent for double-checking your answers. After solving a problem manually, use the calculator to verify your final results.
- Leverage Graphing Tools – Graphing calculators are particularly helpful for visualizing functions and understanding their behavior. Use graphs to verify trends, intercepts, and asymptotes when applicable.
- Avoid Overuse – Relying on a calculator for every calculation can make you dependent on it and hinder your conceptual understanding. Always ensure that you can solve problems manually before turning to the calculator.
By using your calculator wisely and strategically, you can maximize its benefits while also ensuring that you retain a solid grasp of the material and its underlying principles.
Breaking Down Complex Problems
When faced with intricate mathematical questions, the key to solving them lies in breaking them into smaller, manageable steps. Instead of being overwhelmed by the complexity, it’s essential to analyze the problem systematically. By identifying patterns, extracting important information, and applying the right techniques step-by-step, even the most challenging tasks become easier to tackle.
Step-by-Step Approach
Here is a recommended approach for breaking down complex problems:
- Understand the Question – Begin by carefully reading the problem and ensuring that you understand exactly what is being asked. Identify key variables, known values, and what needs to be solved.
- Organize Information – Write down the given data and equations in an organized manner. Visual aids such as diagrams or graphs can be helpful to clarify relationships between variables.
- Identify Key Techniques – Determine which methods or formulas are needed for the solution. Break the problem into sub-problems that can each be solved individually.
- Execute the Plan – Follow through with your calculations, solving each part of the problem one step at a time. Make sure to stay organized to avoid confusion.
- Review Your Work – Once the problem is solved, double-check each step to ensure no mistakes were made. It’s also important to assess whether the result makes sense in the context of the problem.
Common Pitfalls and How to Avoid Them
While working through complex tasks, it’s easy to overlook small details or make errors in calculations. Here are some common pitfalls to watch out for:
- Misinterpreting the Question – Always read the problem carefully to avoid misunderstanding what is being asked.
- Skipping Steps – Skipping steps or rushing through can lead to missing important information or making calculation errors.
- Overcomplicating the Solution – Often, the solution may be simpler than it seems. Look for ways to simplify the problem before diving into complex methods.
By following a structured approach and being mindful of potential errors, you can effectively solve even the most complex mathematical problems with confidence.
Reviewing Derivatives and Integrals
In the study of mathematical analysis, two essential operations are frequently used to understand various concepts such as rates of change and accumulation. These operations–differentiation and integration–form the foundation for solving a wide range of problems. By mastering these techniques, you can approach a variety of challenges with confidence, whether you’re analyzing motion, calculating areas, or modeling real-world phenomena. In this section, we will review the key principles behind these operations, with a focus on the methods and rules that are essential for success.
Understanding Derivatives
Derivatives represent the rate of change of a function with respect to one of its variables. They help us understand how quantities change and are used to model motion, growth, and decay. Below are some of the most important rules for differentiating functions:
| Rule | Description |
|---|---|
| Power Rule | For a function f(x) = x^n, the derivative is f'(x) = nx^(n-1). |
| Product Rule | For the product of two functions, f(x) = g(x) * h(x), the derivative is f'(x) = g'(x) * h(x) + g(x) * h'(x). |
| Quotient Rule | If f(x) = g(x) / h(x), then f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / [h(x)]^2. |
| Chain Rule | If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x). |
Understanding Integrals
Integrals are the inverse of derivatives and are used to calculate the accumulation of a quantity over a given interval. This operation is essential for finding areas under curves, calculating volumes, and solving problems involving total accumulation. Below are some of the fundamental rules of integration:
| Rule | Description |
|---|---|
| Power Rule for Integration | If f(x) = x^n, then the integral is ∫x^n dx = (x^(n+1)) / (n+1), for n ≠ -1. |
| Substitution Rule | This rule simplifies integrals by changing the variable of integration. It is particularly useful for composite functions. |
| Integration by Parts | For products of two functions, ∫u(x)v(x) dx = u(x)v(x) – ∫v(x)u'(x) dx. |
| Fundamental Theorem | This theorem links differentiation and integration, showing that the integral of a function’s derivative over an interval is equal to the difference in the function’s values at the interval endpoints. |
Both differentiation and integration are powerful techniques that play a key role in solving problems across a wide range of applications. Whether you are analyzing dynamic systems or computing areas and volumes, understanding these methods is essential for making sense of complex mathematical concepts.
Real-World Applications of Mathematical Analysis
Mathematical techniques used to analyze change and accumulation have far-reaching implications in various fields of science, economics, and engineering. These methods provide tools for solving practical problems that involve rates of change, optimization, and total accumulation. By applying these principles, we can gain insights into complex systems, model real-world phenomena, and make informed decisions. Here are some key areas where these mathematical principles are frequently used:
Physics and Engineering
In physics and engineering, mathematical analysis plays a critical role in modeling and solving problems related to motion, forces, and energy. Some applications include:
- Projectile motion: Describing the path of objects under the influence of gravity, such as a ball being thrown.
- Optimization of materials: Determining the best shape or size for structures to minimize material use while maximizing strength.
- Fluid dynamics: Modeling the flow of liquids and gases, which is crucial in aerodynamics and hydrodynamics.
Economics and Business
In economics and business, these techniques help optimize profits, minimize costs, and understand market behavior. Some practical uses include:
- Cost analysis: Calculating the cost of production over time and identifying the most efficient production level.
- Revenue maximization: Determining the price point that maximizes revenue by analyzing the relationship between price and demand.
- Supply and demand modeling: Understanding how supply and demand curves behave and finding equilibrium prices.
Biology and Medicine
In biology and medicine, these principles are applied to model populations, analyze the growth of diseases, and optimize medical treatments:
- Population growth: Modeling the growth of populations and understanding factors like carrying capacity and birth rates.
- Drug dosage optimization: Determining the best dosage and timing for administering drugs to achieve optimal results.
- Spread of diseases: Analyzing how diseases spread through populations and predicting future outbreaks.
Environmental Science

Environmental science also benefits from mathematical techniques, helping to understand and predict changes in natural systems:
- Climate modeling:
Resources for Further Preparation
To enhance your understanding and problem-solving skills, using a variety of resources is key to deepening your knowledge. A well-rounded study plan incorporates a mix of explanations, practice exercises, and review materials, helping you strengthen both theoretical understanding and practical application. These resources will provide the foundation you need to tackle complex questions with confidence and efficiency.
Online Learning Platforms
Interactive learning platforms provide a convenient and engaging way to review essential concepts and practice problems. These platforms often offer a combination of video tutorials, practice quizzes, and detailed breakdowns of difficult topics. Some notable options include:
- Khan Academy: Offers free, structured lessons across a variety of subjects with interactive quizzes and exercises for deeper learning.
- Coursera: Features courses taught by professors from top universities, allowing learners to access in-depth learning materials.
- EdX: Provides free courses from prestigious institutions, making it possible to study various topics in depth at your own pace.
Practice Materials and Problem Sets

Consistent practice is essential for mastering any subject. Using practice questions and previous materials can help familiarize you with common problem types and question formats. Consider using these resources to fine-tune your skills:
- Official Practice Sets: Websites often provide access to sample problems and solutions, allowing you to simulate real-world challenges.
- Apps for Problem-Solving: Tools like Wolfram Alpha and Desmos help you solve problems step-by-step and visualize the results, enhancing your understanding.
- MIT OpenCourseWare: Provides free access to problem sets, lecture notes, and video courses from MIT, helping you reinforce your learning with real-world applications.
Books and Study Guides
Study guides and textbooks offer structured reviews of core topics, along with practice questions and detailed explanations. These resources help solidify your understanding and prepare you for more complex challenges. Recommended books include:
- “Barron’s Review”: Known for its comprehensive question sets and expert tips to help you navigate through challenging topics.
- “The Princeton Review”: Provides test strategies, practice materials, and in-depth explanations for mastering key concepts.
- “5 Steps to a 5”: Offers a systematic approach with clear study plans, detailed questions, and helpful strategies for success.
Interactive Tools and Applications
In addition to traditional textbooks, digital tools provide a dynamic way to practice and visualize complex concepts. These applications offer instant feedback and detailed solutions, which can help clarify challenging topics. Some useful apps include:
- Quizlet: Allows you to create and review custom flashcards to help reinforce important concepts and terminology.
- Wolfram Alpha: A powerful tool for solving mathematical problems, offering step-by-step explanations and solutions.
- Desmos Graphing Calculator: A highly interactive graphing tool that helps visualize functions, equations, and data sets, which can be crucial for problem-solving.
By integrating these varied resources into your study routine, you can develop a comprehensive understanding and be well-prepared for the challenges ahead. Consistent practice, alongside a strategic approach to learning, will ensure that you are ready to tackle any problems that come your way.
Final Review and Study Plan Tips

As the deadline approaches, organizing your final review and study sessions is crucial for maximizing your readiness. Focusing on core concepts, managing time effectively, and reinforcing your strengths while addressing weaknesses are key strategies. By having a clear plan and sticking to it, you can ensure that you make the most out of your remaining study time.
Effective Time Management
Time management is vital in the final stages of preparation. A well-structured study schedule ensures that you cover all topics without feeling rushed or overwhelmed. Consider breaking down your study sessions into manageable blocks, focusing on specific areas each day. Keep these tips in mind:
- Prioritize weak areas: Identify topics that require more attention and focus on them during your study blocks.
- Balance practice and review: Divide your time between practicing problems and reviewing theoretical concepts to strengthen both areas.
- Include breaks: Avoid burnout by taking short, regular breaks to recharge your focus and energy.
Strategies for Efficient Review
In the final review stages, it’s important to focus on active learning techniques that reinforce your understanding and memory retention. Passive reading is less effective than actively engaging with the material. Use these strategies to maximize your review:
- Practice with past problems: Solving problems from previous years helps familiarize you with the format and difficulty level, while reinforcing key concepts.
- Teach someone else: Explaining concepts to someone else forces you to articulate your understanding, which helps reinforce your knowledge.
- Use flashcards: Create flashcards with formulas, theorems, and key concepts. Reviewing them regularly will enhance memory retention.
By implementing these techniques, you can ensure that your final review is both focused and effective. Staying organized, prioritizing your weaker areas, and actively engaging with the material will help you approach the challenge with confidence and clarity.