
Learning the fundamental principles of shapes, measurements, and spatial relationships is essential for building a solid foundation in mathematics. Whether you’re tackling basic figures or more complex forms, understanding these core elements allows for deeper insights into a variety of problems. The path to mastery involves not just memorizing formulas, but also developing a clear grasp of how they apply to different scenarios.
With the right approach, solving challenges becomes more intuitive. By breaking down problems into manageable steps, anyone can gain confidence in their ability to tackle even the most difficult topics. A combination of practice and a deeper understanding of key strategies ensures long-term success in this area of study.
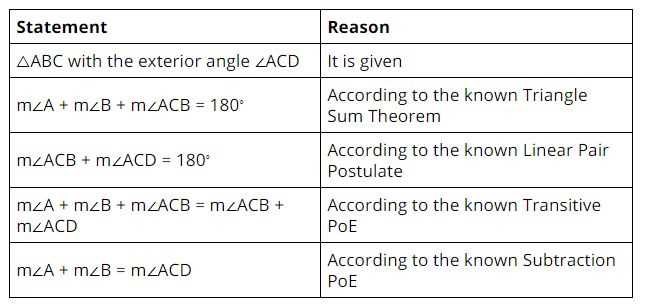
Big Ideas Geometry Answers Overview
Mastering the core principles of shapes, measurements, and spatial reasoning is vital for a comprehensive understanding of this field. The process involves not only learning theoretical concepts but also applying them to real-world scenarios. By exploring different approaches and breaking down complex problems, students can develop effective problem-solving skills and build confidence.
To truly excel, it’s essential to grasp how various formulas and theorems work together to form a cohesive system. This section provides a detailed look at how to approach problems methodically, focusing on key strategies that simplify even the most intricate tasks. With a solid foundation and the right mindset, anyone can enhance their comprehension and achieve better results in this area of study.
Understanding Key Geometry Concepts
Grasping the foundational elements of shapes, their properties, and how they interact in space is crucial for success in this area of study. These core principles form the basis for solving various problems and understanding complex relationships between figures. Whether working with angles, distances, or proportions, it’s essential to build a strong conceptual framework to approach challenges effectively.
Key concepts include the properties of different forms, how they can be measured, and the way they fit into larger patterns. Once these fundamental ideas are understood, they provide a toolkit for tackling a wide range of problems with clarity and precision. A deep comprehension of these concepts is necessary to progress to more advanced topics and to approach exercises with confidence.
How to Approach Geometry Problems

When faced with a challenging task in this field, it’s important to break down the problem into smaller, more manageable parts. Start by carefully analyzing the given information, identifying key elements, and determining what is being asked. This initial understanding helps in choosing the appropriate method to solve the problem, whether it’s through calculation, visualization, or logical reasoning.
Organizing the steps is another critical aspect of tackling these types of problems. By setting a clear sequence of actions, it becomes easier to stay on track and avoid unnecessary complications. Always look for patterns and connections between different aspects of the question, as these often provide clues to the solution.
Practice and repetition play a significant role in becoming more proficient. The more familiar you become with different types of exercises, the more intuitive your approach will become. Over time, you will develop strategies that work best for you, making problem-solving quicker and more efficient.
Exploring Geometry Problem Solving Strategies
Effective problem-solving relies on a mix of creativity and logical thinking. By approaching each challenge with a clear strategy, complex problems become more manageable. One of the first steps is identifying the most relevant information and understanding how different elements of the problem relate to each other. This helps in choosing the most efficient method to find a solution.
Visualizing the problem is a powerful tool in this process. Drawing diagrams or using models allows for a clearer perspective on the relationships between different components. Once the problem is visualized, applying the right formulas or principles can often reveal the solution more quickly.
Another important strategy is working backwards. In some cases, starting from the desired outcome and retracing the steps can lead to a simpler and faster solution. As with any skill, the more you practice these techniques, the more intuitive and effective they become, allowing you to tackle problems with confidence and efficiency.
Common Challenges in Geometry Exercises
While working through problems in this field, students often encounter several common obstacles that can make the process more difficult. These challenges typically arise from either a lack of understanding of the core principles or difficulties in applying these principles to complex problems. Identifying and addressing these issues early can significantly improve performance and confidence.
One frequent challenge is visualizing abstract concepts, especially when dealing with three-dimensional shapes or intricate relationships between figures. Additionally, interpreting problem statements accurately is essential to avoid unnecessary mistakes. Lastly, applying the correct formulas in the right context can be tricky, especially when multiple methods appear applicable.
| Challenge | Solution |
|---|---|
| Poor visualization skills | Practice sketching and using models to improve understanding |
| Misinterpreting problems | Carefully read and break down the problem into smaller parts |
| Confusion over formulas | Review key formulas regularly and understand when to apply them |
Step-by-Step Guide to Solutions
Approaching any challenging problem requires a methodical process to ensure clarity and accuracy. By breaking down each step, it’s possible to systematically move towards the solution. This approach not only simplifies complex tasks but also makes them more manageable and less overwhelming. A clear sequence of actions helps in tracking progress and identifying areas that need further attention.
Step 1: Understand the Problem
The first step in solving any problem is to fully comprehend what is being asked. Carefully read through the question, highlighting important information. This ensures that you are clear about the goal and the given conditions before proceeding with calculations or logic. Understanding the context and key elements of the problem is crucial for choosing the correct approach.
Step 2: Plan and Apply Techniques
Once the problem is understood, plan out the steps needed to solve it. This could involve drawing diagrams, identifying patterns, or selecting relevant formulas. Apply the appropriate techniques based on your understanding, working through each part methodically. If you encounter difficulties, review your steps or try an alternative method until the solution becomes apparent.
Tips for Improving Geometry Skills
Strengthening your skills in this field requires consistent practice and a deeper understanding of the concepts that form its foundation. To excel, it’s important to build a solid grasp of both theoretical knowledge and practical application. By focusing on a few key strategies, you can significantly enhance your ability to solve problems efficiently and confidently.
Practice regularly is one of the most effective ways to improve. The more problems you solve, the more familiar you become with common patterns and techniques. Over time, this repetition helps solidify your understanding and speeds up the problem-solving process.
Focus on understanding the ‘why’ behind formulas and theorems. Simply memorizing rules may not be enough; understanding how and why they work makes it easier to apply them in various contexts. Taking time to reflect on the reasoning behind each solution strengthens your problem-solving skills and ensures you can tackle new challenges with ease.
Role of Practice in Geometry Mastery
Mastering this field of study is largely dependent on consistent practice and refinement of problem-solving techniques. Repetition helps reinforce concepts, allowing students to become more comfortable with different types of challenges. Through continuous engagement, the thought process becomes more intuitive, and complex problems become easier to approach and solve.
Benefits of Regular Practice
Regular practice helps solidify knowledge and improve accuracy when solving problems. As you work through various exercises, you begin to recognize patterns, identify efficient strategies, and improve your speed. This leads to greater confidence and more reliable results in both assignments and exams.
Tracking Progress Over Time
One of the most important aspects of consistent practice is tracking progress. Over time, it’s essential to observe areas of improvement and identify any persistent challenges. This feedback allows for targeted efforts to address weaknesses, ensuring a continuous path towards mastery.
| Practice Frequency | Impact |
|---|---|
| Daily Practice | Faster problem-solving and improved confidence |
| Weekly Review | Reinforces long-term retention and deepens understanding |
| Consistent Reflection | Helps identify areas needing improvement and streamlines learning |
Breaking Down Complex Geometry Questions
Tackling difficult problems requires a methodical approach to break down complex tasks into smaller, manageable components. By dissecting each part of the question, it becomes easier to identify the core elements and apply the appropriate techniques to find a solution. This step-by-step process simplifies what may initially appear overwhelming and allows for more efficient problem-solving.
Steps for Deconstructing a Problem
When faced with a challenging question, follow these steps to systematically approach it:
- Read the problem carefully to ensure full understanding of the given information and what is being asked.
- Identify key elements, such as shapes, angles, or measurements, that are crucial for solving the problem.
- Organize your approach by deciding which principles or formulas are applicable to the situation.
- Break the problem into smaller parts and solve each section step-by-step to avoid confusion.
Common Pitfalls to Avoid
While deconstructing a problem, there are common mistakes to watch for:
- Overlooking important details in the problem statement.
- Failing to apply the correct formulas or methods in the right context.
- Skipping intermediate steps, which can lead to errors in the final solution.
By avoiding these mistakes and following a clear, structured approach, even the most difficult questions become easier to handle and solve accurately.
Geometry Answers for Real-World Applications
The concepts learned in this field extend far beyond the classroom, offering practical solutions to everyday challenges. By applying theoretical principles to real-world situations, one can solve a variety of problems, from designing structures to optimizing space. Understanding how these abstract ideas connect with tangible outcomes is crucial in making informed decisions in various industries.
Applications in Engineering and Architecture
In fields like construction and engineering, the ability to calculate distances, areas, and angles is essential. Whether designing buildings, bridges, or roads, professionals rely heavily on spatial reasoning and mathematical models to ensure precision and safety. This knowledge directly translates into the creation of functional, efficient, and durable structures.
Applications in Technology and Design
Technology also benefits from these principles, particularly in areas like computer graphics, animation, and user interface design. In these fields, understanding proportions, dimensions, and layout is key to creating products that are both visually appealing and functional. Furthermore, the development of cutting-edge devices and systems often requires precise calculations to optimize performance and efficiency.
| Industry | Application |
|---|---|
| Engineering | Designing structural blueprints and calculating material needs |
| Architecture | Space planning, building design, and construction analysis |
| Technology | Creating graphics, simulations, and virtual environments |
Geometry Review for Students

Reviewing foundational concepts is essential for students aiming to strengthen their understanding and perform well in exams. By revisiting core principles and practicing problem-solving, students can identify areas of improvement and reinforce their knowledge. A thorough review helps solidify concepts and prepares students for more complex challenges ahead.
Key Concepts to Focus On
Students should prioritize understanding essential topics such as shapes, angles, measurements, and proportions. Mastery of these core areas forms the basis for solving more advanced problems and applying the concepts in practical situations. Developing fluency in these topics enables students to approach problems with confidence and clarity.
Effective Review Strategies
To maximize review efficiency, students can use techniques such as:
- Practice problems: Consistent exercises help reinforce knowledge and improve accuracy.
- Concept maps: Visualizing connections between different topics aids in understanding relationships.
- Group study: Collaborating with peers allows for different perspectives and deeper insights.
By focusing on these strategies and committing to regular review sessions, students can sharpen their skills and improve their problem-solving abilities.
Effective Methods for Geometry Success
Achieving success in this field relies on a combination of consistent practice, strategic study, and a solid understanding of core principles. To excel, students must develop effective approaches that cater to their learning styles while ensuring a strong grasp of key concepts. Using proven techniques helps simplify complex problems and builds confidence in tackling a wide range of challenges.
Proven Study Techniques
Here are several strategies that can significantly improve performance and mastery:
- Daily Practice: Regularly working on problems helps reinforce concepts and improves problem-solving speed.
- Review Mistakes: Understanding errors and correcting them strengthens comprehension and prevents recurring mistakes.
- Focus on Fundamentals: A solid grasp of basic principles is critical before moving on to more advanced topics.
Maximizing Learning Efficiency
Beyond basic study, there are other methods to enhance learning:
- Active Learning: Engage with the material by teaching it to someone else or discussing it with peers.
- Use Visual Aids: Diagrams, graphs, and models can help clarify abstract concepts and make them more tangible.
- Time Management: Break study sessions into focused intervals with breaks in between to maintain concentration.
By incorporating these methods, students can develop a deeper understanding of the material and achieve consistent success in their studies.
Why Geometry is Important for Learning
This field plays a critical role in developing logical thinking and problem-solving skills. Understanding its principles enables students to make sense of the world around them, from simple shapes to complex structures. Mastery of these concepts strengthens analytical abilities and provides a foundation for various academic and real-life applications.
Core Benefits of Learning This Subject
Here are several key reasons why learning these concepts is essential:
- Enhances Analytical Thinking: It trains the brain to recognize patterns, analyze data, and approach problems from different angles.
- Improves Spatial Awareness: Helps in understanding the properties of shapes and their interactions in space, crucial for fields like architecture and engineering.
- Builds Foundation for Advanced Studies: A solid understanding of this discipline lays the groundwork for more advanced topics in mathematics and science.
Real-World Applications of Knowledge

The importance of mastering these concepts extends beyond academic success. The knowledge gained can be applied in a variety of practical situations, including:
- Design and Construction: Engineers and architects use these principles to create stable, functional, and aesthetically pleasing structures.
- Technology and Animation: Professionals in digital media use these skills to create virtual environments and 3D models.
- Everyday Problem-Solving: Whether organizing space, measuring areas, or navigating maps, these principles offer practical solutions to everyday tasks.
In conclusion, understanding the fundamentals of this discipline is not only essential for academic growth but also for developing valuable skills that can be applied in various careers and day-to-day situations.
Understanding Geometry Through Examples
Real-world examples are crucial in making abstract concepts more tangible and accessible. By exploring practical situations where these principles are applied, students can gain a deeper understanding of how the theoretical knowledge connects to everyday life. Working through examples helps to clarify the steps involved in solving problems and reinforces the reasoning behind key ideas.
Let’s explore a few common scenarios to illustrate the application of basic concepts:
| Example | Concepts Used | Application |
|---|---|---|
| Calculating the area of a triangle | Area formula, base, height | Designing a triangular garden or determining the space required for flooring. |
| Finding the volume of a cylinder | Volume formula, radius, height | Estimating the amount of liquid in a cylindrical tank. |
| Identifying congruent shapes | Symmetry, congruency rules | Designing tiles that fit perfectly together without gaps. |
Through examples like these, it becomes evident how mathematical concepts translate into real-world solutions. Each problem involves identifying the right tools and methods, ultimately leading to an understanding of how abstract principles can be applied to practical challenges.
Key Theorems and Proofs
Understanding core principles and their logical foundations is essential for mastering any mathematical field. In this area of study, various fundamental propositions help explain relationships between different elements, such as angles, lines, and shapes. Theorems provide a framework for proving truths based on accepted axioms and previous results. These results not only strengthen logical reasoning but also offer insights into solving complex problems.
Important Theorems
Here are some of the most crucial theorems in this field, along with their applications:
- Pythagorean Theorem: Describes the relationship between the sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem is widely used in navigation and construction.
- Parallel Postulate: States that if a line segment intersects two lines and forms interior angles less than 180 degrees, then the two lines will eventually meet. It forms the foundation of Euclidean geometry.
- Angle Sum Theorem: In any triangle, the sum of the interior angles equals 180 degrees. This theorem helps in determining the properties of triangles in geometric constructions.
Proof Methods
While theorems provide essential information, the process of proving these statements is equally important. Here are a few common methods used to prove theorems:
- Direct Proof: Involves using known facts and definitions to logically show that a statement is true.
- Indirect Proof: Also known as proof by contradiction, this method assumes the opposite of the statement to show a contradiction, proving the original statement true.
- Proof by Mathematical Induction: Used for proving statements that apply to all natural numbers. The base case is proven first, followed by a proof that if the statement holds for one number, it holds for the next.
Mastering these theorems and proof methods allows individuals to navigate complex problems and understand the logical structure behind geometric relationships. Whether solving practical tasks or working through advanced concepts, these principles are foundational to the subject.
Solutions for Common Topics
Many concepts in the field of mathematics are applicable across various areas of study. Understanding how to approach and solve problems in common themes is essential for building a strong foundation. These themes often involve shapes, measurements, and relationships that appear frequently in both basic and advanced tasks. Below are solutions and methods for solving typical problems encountered in this area.
Key Topics and Solutions
Here are some of the most common topics along with useful strategies for solving related problems:
- Triangles and Their Properties: Understanding the different types of triangles–equilateral, isosceles, and scalene–is critical. Use the Pythagorean theorem for right triangles, and apply the angle sum property to find missing angles.
- Circles and Arcs: For problems involving circles, remember to use the formulas for area and circumference. The relationships between angles and arcs are key to solving questions on sectors and segment areas.
- Coordinate Plane: Solving problems on a coordinate plane requires an understanding of distance, midpoints, and slope. The distance formula and the equation of a line are useful tools in this context.
Solving Techniques
Here are effective techniques for approaching these topics:
- Visualize the Problem: Drawing diagrams or graphs can help you better understand the relationships between different elements and simplify the solution process.
- Apply Known Formulas: Using formulas for areas, volumes, and angles allows you to solve problems more efficiently. Make sure to understand when and how each formula applies.
- Break the Problem Down: Complex problems can often be solved by breaking them into smaller, manageable parts. Focus on solving one step at a time.
By familiarizing yourself with these common topics and applying the appropriate strategies, you can navigate through typical problems and enhance your understanding of this subject.
How to Use Resources Effectively
In any area of study, using available materials efficiently can make a significant difference in your learning process. Resources such as textbooks, online tools, tutorials, and practice exercises offer valuable insights and problem-solving techniques. The key lies in knowing how to access and utilize these resources in a structured way, so you can maximize your understanding and application of the concepts.
To make the most out of the materials at your disposal, start by identifying your needs and gaps in knowledge. Once you know what areas require more focus, select the most relevant resources to address those specific concepts. For example, if you’re struggling with certain problem types, seeking out targeted practice problems can be highly beneficial.
Additionally, it’s important to engage actively with the material rather than passively reading or watching. Practice regularly, take notes, and solve problems step-by-step. Many resources also provide feedback, which can help you identify areas that need more attention. Applying the information in different contexts and revisiting problems periodically can reinforce your understanding.
In short, resources can serve as powerful tools for mastering challenging topics, but success depends on how you approach and interact with them. By using them strategically and practicing consistently, you’ll be able to navigate through complex concepts with greater ease.