
In this section, we delve into the fundamental principles and problem-solving techniques that are essential for mastering complex mathematical concepts. The focus is on developing a deeper understanding of how to approach and solve various challenges that arise in more advanced levels of study. Through a systematic exploration, students are equipped with the tools needed to tackle intricate problems with confidence.
To achieve success, it is crucial to not only grasp the core ideas but also to practice applying them in diverse scenarios. By breaking down each problem into manageable steps, learners can enhance their critical thinking and analytical skills. This approach not only aids in understanding but also fosters the ability to think logically and solve problems efficiently.
Throughout this section, various strategies are presented to help clarify difficult problems, offering insights into more efficient methods of finding solutions. Emphasis is placed on using clear and structured reasoning, which is vital in advancing mathematical proficiency and preparing for more challenging topics ahead.
Core Connections Geometry Chapter 7 Answers
This section focuses on providing the solutions and step-by-step explanations for the various mathematical problems presented. The goal is to help learners better understand the logic and techniques needed to solve complex challenges in this area of study. By breaking down each problem into simpler, more manageable components, students can improve their ability to tackle similar problems in the future.
By following clear and structured steps, the solutions aim to guide readers through the process of analyzing and resolving intricate tasks. It is essential to approach each question with a methodical mindset, ensuring that all necessary concepts are applied accurately. Below is a table summarizing key results and explanations to enhance understanding.
| Problem Number | Solution | Explanation |
|---|---|---|
| 1 | 12 | Begin by applying the distributive property to simplify the expression. |
| 2 | 36 | Use the Pythagorean theorem to solve for the missing side. |
| 3 | 8 | Factor the quadratic equation and solve for the roots. |
| 4 | 45 | Apply angle relationships to determine the unknown measure. |
Understanding Chapter 7 Concepts
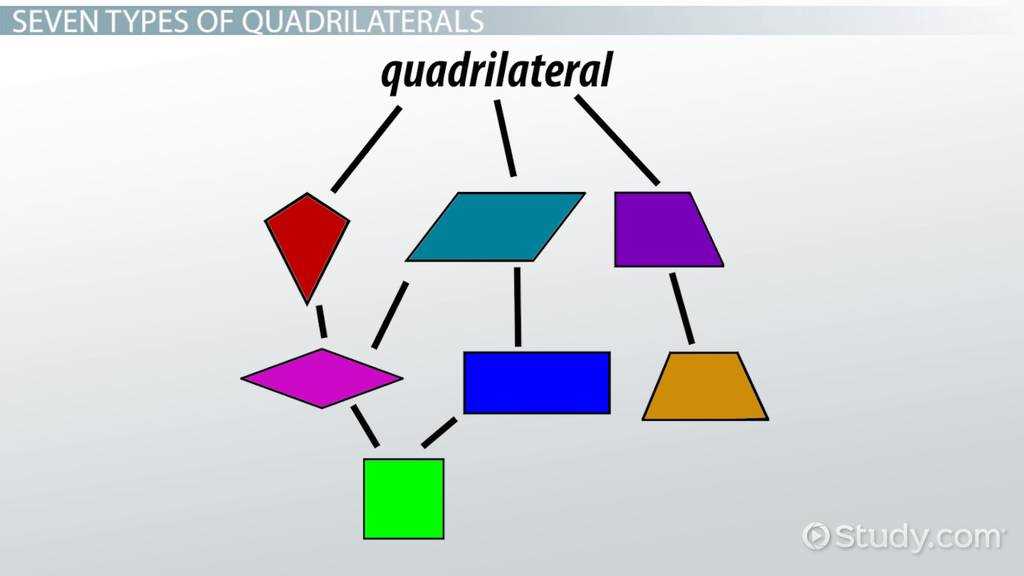
This section covers the essential principles and ideas that form the foundation for solving complex mathematical problems. It emphasizes the importance of grasping key concepts that enable learners to approach problems systematically and effectively. By understanding the underlying theories, students can better navigate through various tasks and enhance their problem-solving skills.
The main focus is on building a strong conceptual framework, where each new idea is connected to previously learned material. This helps to create a comprehensive understanding that allows for the application of multiple strategies to solve diverse problems. The goal is to equip students with the necessary tools to analyze and interpret various mathematical situations with clarity and confidence.
Key Topics Covered in Chapter 7
This section focuses on the critical concepts that are explored in the seventh unit, providing students with a detailed understanding of the key areas of study. These topics are designed to enhance both conceptual knowledge and practical problem-solving abilities, forming a foundation for more advanced topics in mathematics.
Among the important subjects addressed are:
- The relationship between different geometric shapes and their properties
- Methods for solving equations involving angles and side lengths
- Understanding theorems that explain geometric relationships
- Techniques for applying formulas in various contexts
- Strategies for analyzing complex geometric figures
Each of these areas plays a vital role in preparing students for future challenges and allows them to develop a well-rounded approach to solving related problems. By mastering these topics, learners will be able to tackle increasingly difficult mathematical tasks with confidence.
Important Formulas for Geometry Problems
Understanding and applying key mathematical formulas is essential for solving complex problems in this area of study. These formulas are the building blocks for analyzing shapes, angles, and relationships between different geometric elements. Mastering these essential equations will not only aid in completing exercises accurately but also improve overall problem-solving abilities.
Below is a table of some of the most commonly used formulas in solving geometric problems:
| Formula | Application | Explanation |
|---|---|---|
| Area of a Triangle: A = 1/2 × base × height | Finding the area of triangles | This formula calculates the space enclosed within a triangle, using its base and height. |
| Area of a Circle: A = π × radius² | Determining the area of circular shapes | The area of a circle is calculated by squaring the radius and multiplying by π. |
| Perimeter of a Rectangle: P = 2 × (length + width) | Calculating the perimeter of rectangles | The perimeter is found by adding the length and width, then doubling the result. |
| Pythagorean Theorem: a² + b² = c² | Solving right triangles | This theorem relates the sides of a right triangle, where c is the hypotenuse. |
| Volume of a Cube: V = side³ | Finding the volume of a cube | Volume is calculated by cubing the length of one side of the cube. |
By regularly practicing with these formulas, students can gain a better understanding of how to apply them in different contexts, improving their skills in solving various mathematical challenges.
Step-by-Step Solutions to Problems
Breaking down complex problems into manageable steps is essential for understanding and solving them effectively. By following a structured approach, students can better analyze each component of the problem and apply the appropriate techniques to reach the correct solution. This method not only aids in problem-solving but also helps in reinforcing the understanding of key concepts.
Example 1: Solving for Missing Angles
When tasked with finding missing angles in a polygon, start by identifying known values. Apply the angle sum property of the shape and solve for the unknowns step by step. For instance, in a triangle, the sum of all angles equals 180°. If two angles are given, subtract their sum from 180° to find the third angle.
Example 2: Applying the Pythagorean Theorem
In right-angled triangles, the Pythagorean theorem is a powerful tool to determine the length of a side. Start by identifying the two sides you know (the legs) and the one you need to find (the hypotenuse). Use the formula a² + b² = c², where a and b are the legs and c is the hypotenuse. By rearranging the equation, you can solve for the missing side.
Following this step-by-step approach ensures clarity in problem-solving, helping students tackle various types of mathematical tasks with greater confidence and accuracy.
Common Mistakes to Avoid in Geometry
In mathematical problem-solving, certain mistakes can hinder progress and lead to incorrect solutions. Being aware of these common errors allows students to avoid them and strengthen their understanding of the material. Recognizing these pitfalls early can significantly improve accuracy and efficiency in solving complex problems.
Misapplying Theorems and Formulas
A frequent mistake is misapplying theorems or formulas in situations where they don’t fit. For example, using the Pythagorean theorem for non-right triangles or applying area formulas for the wrong shape can lead to incorrect answers. Always ensure that the formula or theorem is relevant to the specific problem before applying it.
Overlooking Units and Precision
Another common error is neglecting units or ignoring the level of precision required. In geometric calculations, it is crucial to include appropriate units for each measurement, such as centimeters or meters, and round results to the necessary number of decimal places. Omitting these details can result in incomplete or misleading answers.
By being mindful of these common mistakes and double-checking work, students can enhance their problem-solving skills and avoid unnecessary errors, ensuring more accurate and reliable results.
How to Approach Core Connections Questions
When tackling mathematical problems, it is essential to approach each question systematically and logically. Developing a step-by-step strategy ensures that all aspects of the problem are addressed, and helps avoid mistakes that might arise from rushing or skipping over details. A well-planned approach allows for more effective problem-solving and a deeper understanding of the material.
The first step is to carefully read the problem and identify what is being asked. Look for key information, such as known values, required outcomes, and any conditions that apply. Once the problem is fully understood, break it down into smaller, manageable steps. This methodical approach will help organize the solution process and reduce the risk of overlooking important aspects.
Next, consider any relevant concepts or formulas that apply to the problem. If the question involves geometry, for example, review any related theorems or properties that could help simplify the calculations. Always check that the correct formula is used for the situation at hand, and ensure it is applied correctly to avoid errors.
Finally, after completing the solution, double-check each step to confirm that no mistakes were made. Reassess the answer to ensure it is reasonable and aligns with the original question. By following these steps, you can approach each problem with greater confidence and accuracy.
Strategies for Effective Learning in Mathematics
Mastering complex mathematical concepts requires a well-organized approach and effective strategies. By applying specific techniques, students can grasp difficult topics more easily and improve their problem-solving abilities. Consistency, active engagement, and practice are crucial for deepening understanding and achieving long-term retention of key principles.
Active Engagement with Problems
One of the most effective methods for mastering mathematical concepts is to actively engage with practice problems. Rather than just reading through examples, solving problems hands-on helps reinforce learned concepts and improves retention. The more actively a student engages, the better they can identify patterns and apply the material in new contexts.
Visual Learning and Diagram Usage
Mathematics often involves spatial reasoning and relationships between shapes or numbers. Utilizing visual aids such as diagrams, graphs, and tables can help students visualize these relationships. Drawing out problems and solutions makes abstract ideas more tangible and aids in understanding how various elements interact.
| Strategy | Benefit |
|---|---|
| Active Problem Solving | Strengthens understanding and improves retention |
| Visual Tools (Diagrams/Graphs) | Helps students see relationships and connections |
| Study Groups | Encourages collaboration and deeper understanding |
| Online Resources | Provides additional practice and varied explanations |
By integrating these strategies into their study routine, students can approach mathematical challenges with greater confidence, enhance their ability to apply concepts, and achieve higher levels of success in their studies.
Clarifying Difficult Problems
Some mathematical problems can seem particularly challenging at first glance. These problems often involve intricate steps or require a deep understanding of underlying principles. However, with the right approach, any complex problem can be broken down into simpler parts. By focusing on the key concepts and following a systematic process, it becomes easier to find solutions and grasp difficult ideas.
Identifying Key Concepts
The first step in solving difficult problems is to identify the core concepts being tested. This requires reading the problem carefully and noting any important information provided. Once the essential elements are highlighted, it becomes easier to apply relevant formulas and theorems. Understanding which concepts are in play can help eliminate confusion and guide you towards the right solution.
Step-by-Step Problem Breakdown
Breaking down the problem into smaller, manageable parts is crucial. Start by solving the problem in stages rather than attempting to solve it all at once. This method prevents feeling overwhelmed and helps ensure that each part of the solution is addressed thoroughly. Checking the work after each step can help spot any mistakes before moving on to the next stage.
By employing these techniques, students can clarify even the most challenging problems and build a stronger foundation in their understanding. Each problem becomes less intimidating when approached with a clear, logical strategy.
Visual Aids and Diagrams for Understanding
When tackling complex topics, visual aids can be incredibly effective in enhancing understanding. Diagrams, charts, and other visual tools simplify abstract concepts, making them more accessible. By visualizing relationships and structures, students can connect the theoretical with the practical, leading to a clearer grasp of the material.
Diagrams play a crucial role in illustrating spatial relationships, especially when dealing with shapes, angles, or figures. Drawing out problems or seeing them represented visually can help identify key elements and their interrelations. This approach is especially useful when working with geometric or algebraic problems, as it allows for a better understanding of how different parts of a problem fit together.
Charts and Graphs are valuable tools for organizing data and recognizing patterns. They provide a clear, concise way to compare values, track changes, or spot trends. By translating information into a visual format, students are more likely to retain key details and identify connections that might be overlooked in text alone.
Utilizing visual aids effectively requires practice and an active approach to learning. By incorporating these tools into study routines, students can enhance comprehension and improve problem-solving skills.
Practice Exercises for Chapter 7
Consistent practice is one of the most effective ways to master complex concepts. By working through exercises, students can reinforce their understanding, identify areas where they need more focus, and improve problem-solving skills. The following exercises provide opportunities to apply learned principles and sharpen mathematical abilities.
Exercise 1: Basic Problem Solving

This exercise focuses on applying fundamental principles to straightforward problems. These types of questions help solidify the understanding of basic concepts and prepare you for more advanced challenges.
Exercise 2: Advanced Application
For a deeper understanding, this exercise involves more complex problems that require multiple steps to solve. These questions challenge you to apply concepts creatively and test your ability to think critically under pressure.
| Problem Type | Description | Difficulty Level |
|---|---|---|
| Basic Solving | Simple problems to reinforce fundamental concepts | Easy |
| Complex Application | Multistep problems requiring critical thinking | Hard |
Completing these exercises will help you build confidence in applying the principles you’ve learned and prepare you for even more challenging material. The key to success is persistence and consistency in practice.
How Geometry Chapter 7 Builds Skills
Mastering mathematical concepts requires both theoretical understanding and practical application. The seventh unit of this course plays a crucial role in developing a wide range of skills that are essential for success in more advanced topics. By engaging with the material, students can sharpen their problem-solving abilities, improve their analytical thinking, and enhance their understanding of spatial relationships.
This section encourages learners to approach problems systematically and apply learned techniques to new situations. Below are some of the key skills developed throughout the unit:
- Problem-Solving Techniques: Learning how to break down complex problems into manageable steps allows for greater success in tackling more difficult challenges.
- Critical Thinking: By engaging with multi-step problems, students develop the ability to think critically and evaluate different possible solutions.
- Logical Reasoning: This unit reinforces the importance of logical reasoning, where each solution builds on previous steps in a clear, sequential manner.
- Spatial Awareness: Understanding and visualizing shapes, sizes, and angles improves the ability to interpret and solve spatial problems accurately.
- Attention to Detail: This section requires a focus on precision, ensuring that each element of a problem is correctly applied to achieve the right answer.
By working through various types of problems, learners are not only reinforcing specific concepts but also honing the skills that are essential in many real-world applications. These abilities form the foundation for more complex mathematical challenges and future studies.
Problem Solving Tips for Success
Effective problem solving in mathematics requires a combination of strategy, practice, and a clear understanding of the principles involved. To navigate through complex tasks, it is essential to apply structured methods and think critically at every step. The following tips will help you approach problems with confidence and clarity.
1. Break Down the Problem
When faced with a challenging question, it’s important to break it down into smaller, manageable parts. Identify what is being asked and focus on one aspect at a time. This can simplify the process and make the problem less overwhelming.
2. Visualize the Problem
Sometimes, seeing the problem can make all the difference. Drawing diagrams or creating visual representations can help you better understand the relationships between different elements. This technique is particularly useful for spatial and shape-related questions.
3. Review Key Formulas
Before attempting a solution, ensure that you are familiar with the relevant formulas. These formulas provide the foundation for solving many types of problems and can guide you through the process efficiently.
4. Eliminate Impossible Answers
In multiple-choice or problem-solving scenarios, start by eliminating answers that are clearly incorrect. This narrows down your options and increases the chances of selecting the correct solution.
5. Check Your Work
Always double-check your calculations and reasoning before finalizing your answer. Small errors can lead to incorrect conclusions, so a careful review is crucial to ensure accuracy.
6. Practice Regularly
The more problems you solve, the more comfortable you become with different types of questions. Consistent practice helps reinforce key concepts and improves your problem-solving speed and accuracy.
By incorporating these strategies into your study routine, you can improve your mathematical skills and increase your ability to solve problems effectively. The key is to approach each problem methodically and stay persistent in your efforts.
Explaining Proofs in Detail
Understanding and constructing proofs is a fundamental skill in mathematics. These logical arguments help establish the truth of geometric statements by systematically applying established facts and principles. In this section, we will break down the steps involved in creating a proof, clarifying common methods, and providing a structured approach to solving problems.
Step-by-Step Breakdown of a Proof
A proof typically involves several key components that must be addressed in a logical sequence. Here’s how to approach a geometric proof effectively:
- Identify Known Information: Start by noting down all the given data, including angles, lengths, or other properties mentioned in the problem. These facts will serve as the foundation of your reasoning.
- State the Goal: Clearly define what needs to be proven. This helps focus the proof and ensures you are working toward the correct conclusion.
- Use Definitions and Postulates: Apply relevant definitions, axioms, or postulates to establish relationships between the elements in the problem. These basic principles are crucial for the logical progression of the proof.
- Formulate Logical Steps: Progress through the proof step by step, ensuring that each statement logically follows from the previous one. Use deductive reasoning to connect facts and derive new information.
- Conclude with the Proof: Once all necessary steps have been demonstrated, conclude by summarizing the proof and showing that the goal has been achieved.
Common Techniques in Proofs
There are several common methods used in proofs, each suitable for different types of problems. Familiarity with these techniques will help you approach geometric challenges with confidence:
- Direct Proof: In a direct proof, you start with known facts and apply logical reasoning to arrive at the conclusion. This is the most straightforward method.
- Proof by Contradiction: This technique involves assuming the opposite of what you want to prove and demonstrating that this assumption leads to a contradiction. The contradiction then proves that the original statement must be true.
- Inductive Proof: In some cases, a proof may involve generalizing from specific cases. Inductive reasoning is often used in sequences and series to establish patterns or relationships.
- Proof by Exhaustion: This method involves checking all possible cases in a situation. It is often used when there are only a few possibilities that need to be considered individually.
By following these steps and employing the appropriate techniques, constructing and understanding geometric proofs becomes a manageable and systematic task. Practicing different types of proofs will improve your mathematical reasoning and help you build a strong foundation in the subject.
Exploring Advanced Topics in Chapter 7
This section delves into some of the more complex concepts presented in the material. While the foundational principles have been established, these advanced topics expand on the basics, offering deeper insights and introducing more challenging problems. Understanding these advanced techniques is essential for building a comprehensive grasp of the subject and applying it to more intricate scenarios.
Advanced Theorems and Principles
As you progress through the material, you’ll encounter theorems that extend basic properties, allowing for the exploration of more complex geometric relationships. These principles not only strengthen your logical reasoning but also open up new ways to approach problems. Below are some key advanced topics:
- Transformations: Investigating how geometric figures can be altered through translations, rotations, reflections, and dilations. These operations form the basis of understanding symmetry and congruence in a variety of contexts.
- Coordinate Geometry: Using algebraic methods to analyze geometric problems, this area bridges the gap between algebra and spatial reasoning, enabling the solution of problems involving lines, curves, and shapes using equations.
- Advanced Proof Techniques: Beyond basic reasoning, advanced proofs often involve intricate logical structures, such as proof by induction, contrapositive, or contradiction, each of which is valuable in solving more sophisticated problems.
- Non-Euclidean Geometry: Exploring alternative geometries that deviate from the traditional Euclidean framework. This includes spherical and hyperbolic geometry, which are crucial for understanding the behavior of shapes and spaces in more complex environments.
Applications of Advanced Concepts
These advanced topics have practical applications in various fields, including architecture, engineering, computer graphics, and physics. By understanding these concepts, you’ll be able to tackle a broader range of problems and see their relevance in real-world scenarios.
- Design and Architecture: Transformations and coordinate geometry are frequently used in design, enabling the creation of accurate models and blueprints for buildings, structures, and landscapes.
- Physics and Engineering: Advanced geometry plays a key role in modeling physical systems, from structural design to understanding motion and forces in multidimensional spaces.
- Technology and Computer Science: In areas like computer graphics, advanced principles are essential for rendering 3D environments and simulating physical phenomena in virtual spaces.
By mastering these advanced topics, you’ll not only enhance your mathematical understanding but also gain the tools needed to solve higher-level problems in both academic and practical settings.
How Chapter 7 Prepares for Exams
This section serves as a bridge between theoretical understanding and real-world application, helping students to prepare effectively for upcoming assessments. By focusing on the key concepts, methods, and problem-solving techniques introduced throughout the material, learners can gain a solid foundation for tackling exam questions. The skills acquired in this part of the study guide not only reinforce the basic principles but also provide the necessary tools for handling more complex scenarios often encountered in test situations.
Through a series of practice problems, real-life applications, and detailed explanations, students are guided step-by-step in their learning journey. This approach ensures that they are well-equipped to address various types of questions, ranging from basic calculations to more involved theoretical challenges. Whether reviewing fundamental concepts or exploring advanced techniques, the exercises in this section serve to reinforce and consolidate knowledge, ensuring students are exam-ready.
The structured format of this section also encourages strategic study habits. By focusing on key areas like logical reasoning, proof development, and spatial awareness, students are taught to approach problems systematically and efficiently, which is crucial for time management during exams. With plenty of practice and guidance, learners will feel confident in their ability to navigate through the exam material with ease.
Understanding Methodology for Effective Learning
This approach to learning emphasizes a structured framework designed to foster a deeper understanding of mathematical concepts. It focuses on making connections between various ideas and building a solid foundation that can be applied to both simple and complex problems. The methodology encourages students to not only memorize formulas and rules but also to understand the reasoning behind them, enabling them to tackle unfamiliar problems with confidence.
Key Principles of the Methodology
- Building Conceptual Understanding: The emphasis is placed on understanding the “why” behind each concept, allowing students to see the bigger picture and how individual ideas are interconnected.
- Step-by-Step Problem Solving: The method breaks down complex problems into smaller, manageable steps. This approach helps students to logically progress from one stage to the next, reducing the likelihood of errors and confusion.
- Practical Application: Real-world examples are used to illustrate theoretical concepts, demonstrating their relevance and helping students grasp their practical significance.
Benefits of the Approach
- Improved Retention: By engaging with concepts in a meaningful way, students are more likely to retain the information in the long term, rather than simply memorizing it for exams.
- Enhanced Critical Thinking: This method encourages students to analyze problems from different angles, fostering a mindset of critical thinking and problem-solving.
- Increased Confidence: As students become more comfortable with the material, they gain confidence in their ability to approach even challenging problems with ease.
Improving Your Problem-Solving Speed
Speed in solving mathematical challenges is a skill that can be developed with practice and the right strategies. Mastering this ability involves not only understanding the concepts but also becoming proficient at recognizing patterns, applying shortcuts, and maintaining focus under time pressure. The key is to build a solid foundation of knowledge while learning how to quickly identify the most effective approach for each problem.
Effective Strategies for Faster Problem Solving
- Familiarity with Key Concepts: The more familiar you are with core principles, the faster you can recognize which methods or formulas to apply. Review important theorems, properties, and methods regularly to improve recall under pressure.
- Practice with Timed Exercises: Set a timer while solving problems to simulate real exam conditions. This helps train your mind to think quickly and efficiently, reducing unnecessary steps and errors.
- Work on Visualizing Problems: Visualization can speed up problem solving significantly. Try to picture the problem in your mind or sketch a diagram, as this can often simplify complex tasks and provide immediate insight into the solution.
Common Mistakes to Avoid
- Rushing Without Understanding: Speed should not come at the cost of comprehension. Make sure you understand the problem before jumping to a solution. Rushing through without a clear strategy can lead to careless mistakes.
- Overlooking Simple Shortcuts: Many problems have shortcuts that can save time. Recognizing these patterns early can cut down the time you spend on calculations.
- Skipping Steps: While it’s tempting to skip steps when you’re in a rush, doing so can lead to mistakes. Always ensure you follow the necessary steps to avoid errors, even if it takes a bit longer.