
Mathematics often presents challenges that require a deep understanding of various concepts and techniques. Whether you’re tackling complex shapes, calculating measurements, or solving intricate puzzles, the ability to approach these problems with the right strategies is crucial for success.
In this section, we will explore effective methods and strategies that can help simplify these tasks. From foundational knowledge to advanced problem-solving techniques, the focus will be on breaking down each step and ensuring a thorough comprehension of the material.
With consistent practice and the right tools, overcoming these challenges becomes much more manageable. This guide will provide you with the necessary skills to confidently solve even the most difficult problems.
Solving Complex Mathematical Problems
When it comes to tackling mathematical challenges, having a structured approach is essential. This section focuses on providing solutions to a wide range of problems, from basic principles to more intricate calculations. By following a logical progression, you can better understand the key concepts and techniques needed to solve each problem effectively.
Breaking Down the Problem
Understanding the question at hand is the first step toward finding a solution. Carefully analyzing the problem and identifying relevant information allows you to create a strategy. Focus on recognizing patterns, applying known rules, and breaking the problem into manageable steps. This approach makes it easier to navigate complex scenarios and find the correct answer.
Developing Practical Solutions
Once the problem is broken down, the next step is applying the appropriate methods to arrive at a solution. Whether it’s through algebraic calculations, visualizing concepts, or using formulas, each method can help lead to the correct result. With enough practice, these solutions become more intuitive, and the process of solving becomes quicker and more efficient.
Understanding the Basics of Geometry
Building a strong foundation in mathematical concepts is essential for solving more complex problems. This section focuses on the fundamental principles that serve as the building blocks for more advanced topics. Grasping the basics provides the necessary tools to approach and solve challenges with confidence.
Key Shapes and Their Properties
One of the first areas to explore is the study of various shapes and their properties. Understanding the characteristics of common figures such as squares, circles, and triangles is crucial. Each shape has unique properties, such as angles, side lengths, and symmetry, that help in solving related problems.
Understanding Measurement and Relationships
Measurement plays a central role in this field. Recognizing how to calculate distances, areas, and volumes is essential for finding precise solutions. Additionally, understanding the relationships between angles, lines, and surfaces is key to solving more complex scenarios.
Key Concepts in Mathematical Problem Solving
Mastering fundamental concepts is essential for tackling a wide range of mathematical challenges. This section explores the core ideas that provide the foundation for more advanced problem-solving techniques. A strong grasp of these concepts allows for a deeper understanding of complex problems and enhances one’s ability to find accurate solutions.
Key principles such as relationships between angles, properties of shapes, and formulas for calculating area and volume are crucial. Understanding these core ideas allows for effective application in various mathematical scenarios, whether in abstract reasoning or real-world problem solving.
How CPM Geometry Improves Problem Solving

Developing a structured approach to solving mathematical problems greatly enhances one’s ability to tackle complex challenges. By focusing on critical thinking and logical steps, students can strengthen their problem-solving skills and build confidence in addressing even the most difficult tasks.
One of the key benefits of learning through this method is the ability to break down problems into smaller, manageable parts. This approach helps in recognizing patterns, applying known principles, and developing solutions with greater precision.
Key Benefits of This Approach
- Improved Understanding: Gaining a deeper understanding of mathematical concepts allows for better application in various situations.
- Step-by-Step Problem Solving: Breaking down complex problems into smaller, more manageable steps improves focus and reduces errors.
- Logical Thinking: Developing logical reasoning skills makes it easier to navigate abstract problems and recognize efficient solutions.
Techniques for Effective Problem Solving
- Identify Key Information: Focus on the essential elements of the problem to streamline the solution process.
- Apply Known Principles: Use established formulas and methods to solve problems faster and with greater accuracy.
- Practice Regularly: Consistent practice helps in reinforcing concepts and developing faster, more efficient problem-solving habits.
Common Challenges in Geometry Problems
Mathematical problems often present a variety of challenges, requiring both creative thinking and a strong understanding of core principles. These obstacles can arise from misinterpreting the problem, failing to apply the correct method, or overlooking critical details. Recognizing and addressing these difficulties is essential for improving problem-solving skills.
Misunderstanding Problem Statements
One of the most common hurdles is a failure to fully grasp the question being asked. Problems can contain complex wording or tricky phrasing that might cause confusion. To avoid this, it’s important to carefully read the problem, identify key information, and break it down into simpler components before proceeding.
Incorrect Application of Formulas

Another challenge is applying the wrong formula or method to solve the problem. Sometimes, it’s easy to confuse similar concepts, leading to mistakes in calculations or reasoning. Ensuring that the correct formula is used for the right type of problem is crucial. Regular practice and familiarity with different scenarios can help prevent such errors.
Step-by-Step Approach to Geometry Solutions
A methodical approach is essential when solving mathematical problems, as it helps break down complex tasks into simpler, more manageable steps. By following a clear and organized process, the problem becomes less overwhelming, and the solution path becomes more apparent.
Essential Steps for Solving Problems
- Read the Problem Carefully: Begin by thoroughly understanding what is being asked. Identify key pieces of information and make note of any specific conditions or constraints.
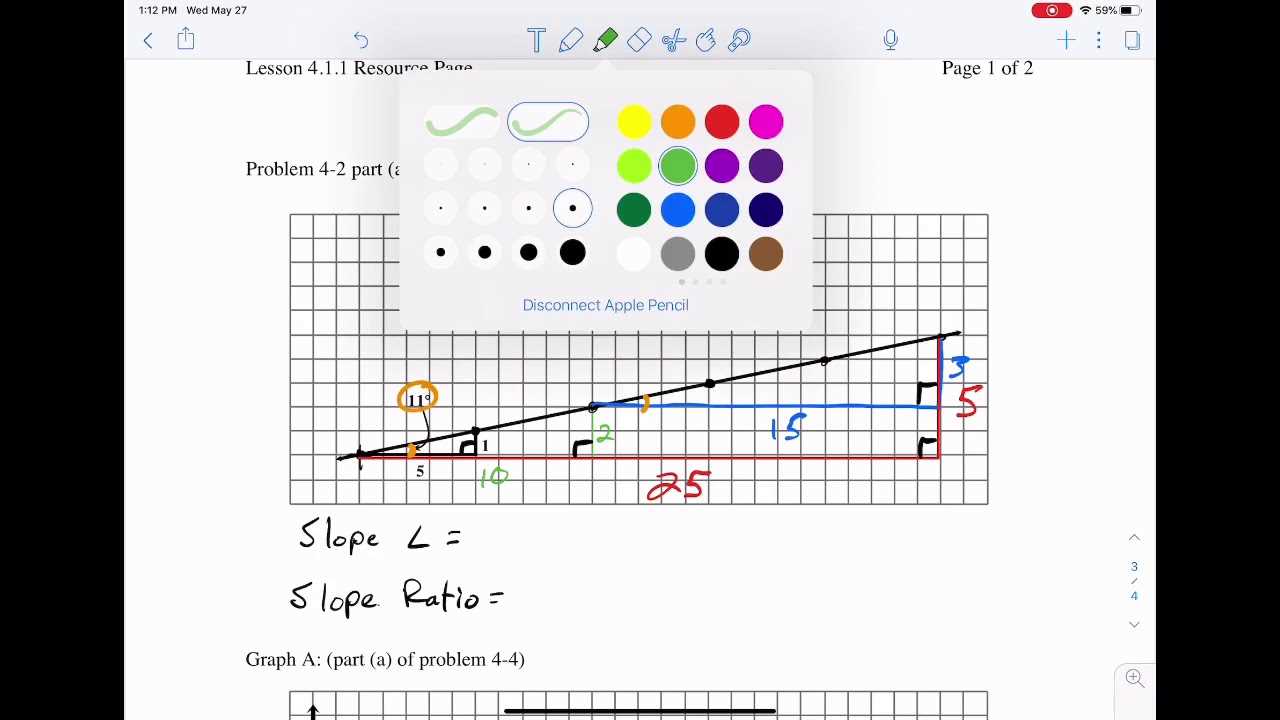
- Sketch a Diagram: Visual aids can often simplify the problem. Draw relevant shapes or figures to represent the situation clearly and accurately.
- Choose the Right Method: Based on the problem’s requirements, decide on the appropriate formula or strategy to apply. This could involve algebraic methods, geometric properties, or logical reasoning.
- Perform Calculations: Apply the chosen method, carefully performing any necessary calculations or logical steps to solve the problem.
- Review the Solution: Once a solution is found, double-check the steps and results. Ensure the answer is reasonable and satisfies all parts of the original question.
Key Considerations During the Process
- Attention to Detail: Pay close attention to every aspect of the problem, from the wording to the diagram. Small details can significantly impact the solution.
- Stay Organized: Keep your work neat and organized to prevent confusion. Writing down each step ensures you don’t overlook important parts of the solution.
Strategies for Mastering Geometry Concepts
Mastering mathematical concepts requires a combination of understanding core principles and consistent practice. To achieve a deep comprehension and improve problem-solving skills, it is essential to employ effective strategies that make learning both efficient and enjoyable.
One key strategy is to actively engage with the material by practicing regularly and applying concepts to real-world problems. Repetition helps reinforce understanding, and working through various problems strengthens both knowledge and confidence.
Another effective approach is to visualize concepts through diagrams or models. This technique helps connect abstract ideas with tangible representations, making complex ideas easier to grasp. It is also crucial to break down difficult topics into smaller, more manageable parts, allowing for focused study of each element.
Importance of Practice in Geometry
Repetition and consistent practice are essential components in mastering any mathematical field. By repeatedly working through problems, learners not only strengthen their understanding of core principles but also develop the skills needed to solve complex problems with ease.
Frequent practice enables the brain to recognize patterns, apply learned methods, and increase overall speed in solving problems. Without regular engagement, it can be difficult to fully internalize concepts and techniques, which may lead to confusion or errors in future tasks.
Benefits of Consistent Practice
- Reinforcement of Key Concepts: Regular practice helps solidify fundamental ideas, making it easier to apply them to new and more complex problems.
- Improved Problem-Solving Speed: The more problems you work through, the faster and more efficient you become at identifying solutions.
- Increased Confidence: With each successful problem solved, your confidence grows, making it easier to tackle more difficult challenges.
Effective Practice Techniques
- Start with Simple Problems: Begin with foundational exercises to ensure a strong grasp of basic principles before progressing to more complex scenarios.
- Challenge Yourself: Gradually increase the difficulty of the problems you tackle. Pushing yourself beyond your comfort zone helps build greater expertise.
- Review Mistakes: Take the time to understand any errors made during practice. Analyzing mistakes helps pinpoint areas that need further attention and improvement.
Effective Methods for Geometry Problem Solving

Approaching mathematical problems requires a strategic mindset to simplify complex tasks and find accurate solutions. By using proven methods, learners can enhance their problem-solving abilities and approach each challenge with greater confidence and precision.
One of the most effective ways to tackle problems is by breaking them down into smaller, more manageable steps. This approach allows for a clearer understanding of the problem and the identification of the most appropriate solution techniques. Another key strategy is to utilize visualization tools such as diagrams, which can make abstract concepts more tangible and easier to manipulate.
Key Methods for Success
- Visualization: Drawing diagrams or models can help in recognizing relationships between elements and clarifying the problem.
- Step-by-Step Approach: Breaking the problem into smaller steps ensures that no detail is overlooked, and each stage is completed methodically.
- Use of Logical Reasoning: Apply deductive reasoning to eliminate possibilities and focus on the most viable solution paths.
Tips for Improving Problem-Solving Skills
- Practice Regularly: The more problems you solve, the quicker and more accurately you can apply methods to new challenges.
- Review and Reflect: After solving a problem, review the process and reflect on any areas where improvements can be made.
- Seek Alternative Approaches: If one method doesn’t seem to work, try a different approach or technique to broaden your understanding of the problem.
Tips for Tackling Difficult Geometry Questions
When faced with challenging mathematical problems, it’s important to remain patient and approach the task methodically. Complex questions may seem overwhelming at first, but breaking them down into simpler steps can help clarify the process and lead to a solution. By employing certain strategies and techniques, learners can gain confidence and improve their ability to handle tough problems.
One of the most effective strategies is to carefully analyze the given information and identify what is being asked. Often, complex problems involve multiple pieces of information that need to be connected in a logical sequence. Taking the time to understand the problem fully is the first step towards finding the correct solution.
Another useful approach is to draw diagrams or visual representations of the problem. This can help make abstract concepts more concrete and allow you to see relationships between different elements. A clear visual aid can often make the difference in understanding how to approach the problem effectively.
Lastly, it is important to remain persistent. Difficult problems can sometimes require multiple attempts or alternative methods before arriving at the correct answer. Keep trying different approaches until the solution becomes clear.
How to Organize Geometry Solutions
Efficiently organizing solutions to mathematical problems is crucial for both clarity and accuracy. By following a structured approach, you can simplify complex tasks and ensure that each step is logically connected. Proper organization also allows you to review your work more easily and spot any mistakes before finalizing your solution.
The first step in organizing solutions is to clearly define the problem and identify the key elements that will guide the solution. This helps you stay focused on the important information and reduces the risk of making unnecessary assumptions. Once the problem is clearly understood, the next step is to break it down into smaller parts and tackle each part step by step.
Step-by-Step Approach
| Step | Action | Purpose |
|---|---|---|
| 1 | Understand the problem | Ensure you know what is being asked and gather all relevant information. |
| 2 | Draw diagrams | Visualize relationships and key elements in the problem. |
| 3 | Break into parts | Divide the problem into manageable steps for easier solving. |
| 4 | Solve step by step | Approach each part individually, applying relevant methods and formulas. |
| 5 | Review the solution | Check for errors and verify that the final result is correct. |
Tips for Effective Organization
- Write out each step clearly: Don’t skip any details, even if they seem minor. This ensures every part of the solution is accounted for.
- Use labels and variables: Clearly label each part of the diagram and use variables to represent unknown values. This makes the problem easier to track.
- Keep your work neat: A tidy layout can prevent confusion, especially when reviewing complex solutions.
Geometry Formulas You Should Know
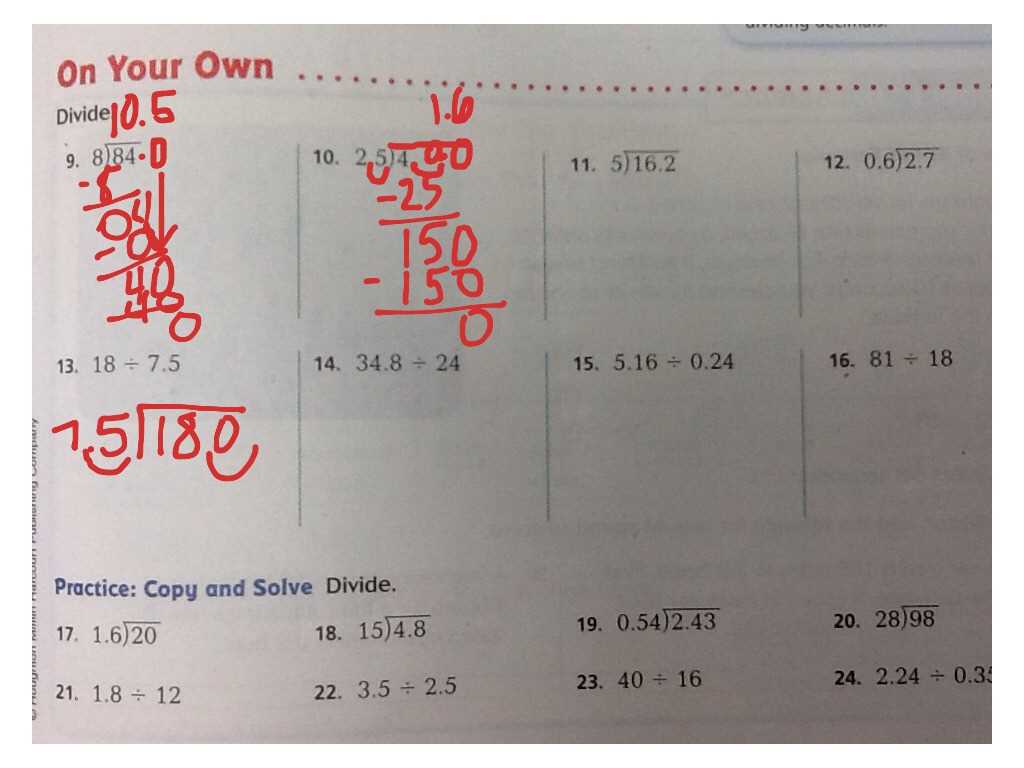
Mastering essential mathematical formulas is key to solving a wide range of problems. These fundamental equations serve as the building blocks for more complex tasks and are often applicable across various types of problems. Knowing when and how to use these formulas can significantly speed up problem-solving and ensure accuracy.
Some of the most frequently used formulas are related to basic shapes and their properties. These include the calculation of area, perimeter, volume, and surface area for common geometric figures. By committing these formulas to memory, you can efficiently approach most problems without needing to derive the equation each time.
Essential Formulas for Common Shapes
- Rectangle:
- Area = length × width
- Perimeter = 2 × (length + width)
- Circle:
- Area = π × radius²
- Circumference = 2 × π × radius
- Triangle:
- Area = ½ × base × height
- Perimeter = side₁ + side₂ + side₃
- Square:
- Area = side²
- Perimeter = 4 × side
Volume and Surface Area Formulas
- Rectangular Prism:
- Volume = length × width × height
- Surface Area = 2 × (length × width + length × height + width × height)
- Sphere:
- Volume = (4/3) × π × radius³
- Surface Area = 4 × π × radius²
- Cylinder:
- Volume = π × radius² × height
- Surface Area = 2 × π × radius × (radius + height)
Visualization Techniques for Geometry Problems
Visualizing mathematical problems is a powerful tool for understanding complex concepts and simplifying problem-solving. By creating clear, accurate representations of the problem, you can see relationships between different elements, identify patterns, and break down the task into manageable parts. This approach often leads to quicker solutions and reduces the likelihood of errors.
One effective method is to draw diagrams that represent the objects or figures in the problem. Even simple sketches can reveal important details and clarify what needs to be calculated. When working with shapes, labels, and measurements can provide additional clarity and help keep track of important information.
Techniques for Effective Visualization
- Draw to Scale: Create accurate drawings where the sizes and proportions of the figures reflect the problem’s values. This helps you see how different parts relate to each other.
- Use Color Coding: Assign different colors to various components of the figure, such as angles, sides, or special lines. This can help highlight important areas and simplify complex diagrams.
- Label Key Elements: Label each part of your diagram, including dimensions, angles, and other relevant variables. This eliminates ambiguity and ensures you’re working with all necessary data.
- Break Down the Problem: If the problem involves multiple steps or components, break the diagram into smaller sections. Solve each part individually before combining them for the final solution.
Using Technology to Aid Visualization
- Graphing Tools: Software or online tools that allow you to graph shapes and figures can provide an interactive way to experiment with different scenarios.
- 3D Modeling: For more complex problems, 3D visualization can help you better understand spatial relationships between objects.
Understanding Geometric Proofs and Theorems
At the core of mathematical reasoning lies the ability to construct valid arguments to support claims or solve problems. Proofs and theorems are essential tools in this process, providing logical frameworks to demonstrate the truth of a statement based on known facts and principles. Developing a solid understanding of these concepts is crucial for mastering various mathematical challenges.
Proofs are systematic arguments that establish the validity of a mathematical claim. They rely on previously established facts, such as definitions, axioms, and prior theorems, to demonstrate that a particular statement must be true under all circumstances. The process of proving a statement is structured, with each step carefully building on the last to arrive at a final conclusion.
Key Elements of Mathematical Proofs
- Definitions: Precise descriptions of mathematical objects and terms that set the foundation for further reasoning.
- Axioms and Postulates: Fundamental truths assumed to be self-evident, which are used as starting points in proofs.
- Logical Steps: The use of deductive reasoning to derive new facts from previously established truths.
- Conclusion: The final step where the initial claim is shown to be true, based on the logical progression of the proof.
Common Types of Proofs
- Direct Proof: Involves starting with known facts and using logical steps to prove a statement directly.
- Proof by Contradiction: Assumes the opposite of the statement to be true and shows that this leads to a contradiction, thus proving the original statement.
- Proof by Induction: Used for statements involving integers, proving a base case and then showing that if the statement holds for one case, it holds for the next.
Common Mistakes in Geometry and How to Avoid Them
Mathematical problems often involve intricate reasoning, and even the smallest error can lead to incorrect conclusions. In particular, working with shapes, figures, and spatial reasoning requires precision. Many common mistakes can hinder progress, but by recognizing these pitfalls, you can avoid them and improve your problem-solving skills.
One frequent error is misunderstanding the properties of shapes. For instance, confusing the characteristics of different types of triangles–such as equilateral, isosceles, and scalene–can lead to incorrect calculations and conclusions. It’s important to recall key properties and definitions before jumping into a solution.
Another common mistake is neglecting to apply correct formulas or forgetting to consider all dimensions. In problems involving areas, volumes, or surface areas, failing to use the right formula or omitting necessary terms can result in inaccurate answers. Always double-check that you’re using the correct equation for the specific scenario.
How to avoid these mistakes:
- Double-check your definitions: Make sure you fully understand the properties of the shapes you’re working with.
- Verify your calculations: Carefully go through each step to ensure all values are applied correctly.
- Take your time: Don’t rush through problems. Rushed work often leads to simple but costly mistakes.
Additionally, another error occurs when assumptions are made without justification. For example, assuming two angles are congruent simply because they appear to be can lead to errors in reasoning. Always support your conclusions with solid evidence or known theorems.
By staying mindful of these common mistakes and approaching problems with patience and precision, you can greatly reduce the likelihood of errors and increase your proficiency in solving complex problems.
How to Use Geometry Tools Effectively
In mathematical problem-solving, using the right tools is crucial for obtaining accurate results. Whether you are working with physical instruments or digital software, knowing how to apply these tools correctly can streamline the process and help you avoid mistakes. The key is understanding each tool’s purpose and using it to its full potential.
Understanding Essential Tools
Several instruments are commonly used when working with shapes and spatial reasoning. Some of the most essential tools include:
| Tool | Purpose | How to Use It |
|---|---|---|
| Ruler | To measure lengths or draw straight lines | Ensure the ruler is aligned properly with the object or points you’re measuring. Use the markings precisely for accuracy. |
| Compass | To draw arcs or circles and measure distances between two points | Keep the compass steady and ensure the point stays fixed while you draw. Check the distance carefully before drawing. |
| Protractor | To measure angles | Place the center of the protractor at the vertex of the angle. Ensure the base aligns with one arm of the angle, then read the measurement on the scale. |
| Calculator | For performing complex calculations | Double-check inputs to avoid errors. Use parentheses appropriately to group terms and get accurate results. |
Maximizing Tool Efficiency
To use these tools effectively, you must practice regularly. The more familiar you become with each tool, the quicker and more accurately you can apply them to solve problems. Here are some tips:
- Maintain precision: Always ensure tools are aligned properly. Even the slightest misalignment can lead to significant errors.
- Double-check measurements: After measuring or drawing, always check your results. Sometimes tools can shift slightly during use, affecting accuracy.
- Understand the tool’s limits: Each tool has its own limitations, so be aware of them. For example, a basic ruler may not measure very small increments as precisely as a caliper would.
By mastering these tools and techniques, you can tackle more complex tasks with confidence and improve the accuracy of your results.
Time Management in Geometry Assignments
Effective time management is crucial when working on complex tasks that involve spatial reasoning and problem-solving. Organizing your approach and allocating enough time for each step can help you avoid unnecessary stress and ensure that you complete assignments accurately and on time. By breaking down your work into manageable chunks, you can stay focused and maximize productivity.
One key strategy is to begin by understanding the requirements of the task and estimating how much time each section will take. Prioritize the most difficult or time-consuming parts and tackle them first while your mind is fresh. This will allow you to give your best effort to the more challenging aspects of the assignment.
Another useful tip is to set specific time limits for each section of the task. For example, decide to spend no more than 15 minutes on a particular problem or set of problems. This can help prevent you from getting bogged down in one area and wasting valuable time.
Finally, make sure to allocate time for review at the end of the assignment. Reviewing your work gives you a chance to spot any mistakes or inconsistencies and correct them before submission. By managing your time effectively, you ensure not only that the work gets done but that it’s completed to the best of your ability.
Additional Resources for Geometry Practice
To strengthen your skills in solving spatial and shape-related problems, it’s important to make use of various resources that cater to different learning needs. By exploring different materials, you can gain a deeper understanding of the concepts and methods required to solve complex tasks. Below are some valuable resources that can enhance your practice and improve your problem-solving abilities.
Books and Textbooks
Books dedicated to spatial reasoning and mathematical problem-solving are a great way to expand your knowledge. Textbooks often include step-by-step examples and a variety of exercises to help reinforce key concepts. Look for materials that cover a wide range of difficulty levels, from introductory to advanced, so you can build up your skills progressively.
Online Platforms and Websites
There are numerous online platforms offering practice problems and tutorials for enhancing spatial problem-solving skills. Websites like Khan Academy, Coursera, and Brilliant provide interactive lessons, quizzes, and explanations that can help clarify difficult topics. Many of these platforms also offer practice problems with immediate feedback, allowing you to gauge your progress.
| Resource | Features | Link |
|---|---|---|
| Khan Academy | Free tutorials, exercises, and video lessons | Khan Academy |
| Brilliant | Interactive problems and expert-created lessons | Brilliant |
| Mathway | Problem solver with step-by-step solutions | Mathway |
By incorporating a mix of these resources into your study routine, you can ensure consistent practice and growth in your problem-solving abilities. Whether you prefer visual learning through video tutorials or engaging with interactive quizzes, these tools will provide a well-rounded approach to mastering complex problems.