Geometry 1.3 Answers Step by Step Guide

Understanding the foundations of mathematical reasoning can significantly enhance problem-solving skills. In this section, we will explore key methods and strategies to tackle common mathematical challenges, helping you develop a deeper grasp of concepts and techniques. By mastering these steps, you’ll be able to approach each question with confidence and precision.

Effective strategies play a crucial role in ensuring that you not only find solutions but also understand the underlying principles that lead to them. Whether you’re dealing with shapes, measurements, or abstract concepts, knowing how to break down each problem systematically can make a big difference.

Through targeted examples and detailed explanations, we’ll guide you through the process of solving complex problems efficiently. With the right approach, you’ll soon find that difficult tasks become more manageable and even intuitive, paving the way for success in future challenges.

Geometry 1.3 Answers Explained

In this section, we will focus on how to approach and solve various mathematical problems effectively. Understanding the steps involved in finding solutions is key to mastering the subject and applying the right methods to each challenge. The goal is to break down complex problems into manageable parts and understand the reasoning behind each step.

Key techniques involve recognizing patterns, using essential formulas, and applying logical reasoning. Whether dealing with spatial relationships, angles, or measurements, having a structured approach allows for a more efficient and accurate resolution of each task. By understanding these techniques, you can apply them to a wide range of similar problems with confidence.

Clarifying the thought process behind each solution ensures that you not only arrive at the correct result but also fully grasp the concepts involved. This deeper understanding leads to improved problem-solving skills that can be used across different mathematical topics.

Understanding Key Concepts in Geometry

To succeed in solving mathematical problems, it’s essential to grasp the core ideas that underpin each task. A strong foundation in the fundamental principles allows for a more intuitive approach to complex questions. In this section, we’ll explore these foundational elements, providing clarity on the most important concepts that guide the problem-solving process.

Shapes and Their Properties

Every geometric problem involves shapes, whether they are simple figures like triangles and squares or more complex forms such as circles and polygons. Understanding the properties of these shapes, such as sides, angles, and symmetry, is crucial. Each property plays a role in determining relationships within the figure and solving for unknown values.

Measurement and Calculation Techniques

Another key concept is how to measure and calculate different aspects of shapes, such as area, perimeter, and volume. Mastery of these calculations allows you to accurately assess and compare geometric figures. Knowing the formulas for these measurements and understanding when to apply them makes solving tasks quicker and more efficient.

Steps to Solve Geometry 1.3 Problems

Solving mathematical challenges effectively requires a clear and structured approach. By following a series of logical steps, you can break down even the most complex tasks into simpler, manageable parts. This section outlines the essential steps to take when tackling any geometric problem, ensuring that you can find solutions methodically and with confidence.

The first step is to carefully read and understand the problem. Take note of all given information, and identify what is being asked. Once you have a clear picture of the situation, sketching a diagram can often help visualize the problem and make relationships between elements more apparent.

Next, apply the appropriate formulas and theorems that relate to the specific figures and measurements involved. This is where knowing the key principles and properties of different shapes becomes crucial. Once you’ve set up the necessary equations, proceed with solving for the unknown values, checking your work as you go to ensure accuracy.

Finally, review your solution and double-check that the answer makes sense within the context of the problem. If possible, verify your results through alternate methods or by comparing with similar problems. A well-checked solution provides both accuracy and a deeper understanding of the material.

How to Approach Geometry Questions

Approaching mathematical problems requires a strategic mindset. Whether dealing with shapes, angles, or measurements, having a clear plan helps you break down the task and systematically find solutions. In this section, we will explore effective techniques to tackle problems with confidence, starting from understanding the question to applying the right methods for resolution.

Understanding the Problem

The first step in solving any mathematical problem is thoroughly understanding the question. Carefully read through the information provided and identify what is being asked. Are you asked to find a specific measurement, prove a relationship, or calculate a value? Knowing exactly what needs to be determined allows you to focus your efforts in the right direction.

Organizing Your Work

Once you understand the problem, organizing your work is key. This involves sketching diagrams, writing down known values, and determining the formulas or principles that apply. By laying out the details systematically, you reduce the chance of overlooking important elements.

Step	Action
1	Read and analyze the problem statement
2	Identify the known values and variables
3	Draw a diagram if necessary
4	Apply the relevant formulas or theorems
5	Check your calculations and solution

By following these steps and maintaining a methodical approach, you can solve problems more effectively and with greater accuracy. It’s not just about getting the right answer, but also about understanding the process behind it.

Common Mistakes in Geometry 1.3

When solving mathematical problems, certain mistakes are more common than others. These errors can stem from a misunderstanding of key concepts, careless calculations, or overlooking important details. Identifying and avoiding these frequent pitfalls will help you improve your accuracy and problem-solving skills.

One common mistake is rushing through the steps without fully understanding the question. Often, a lack of clarity in the problem statement can lead to incorrect assumptions or improper methods being applied. Additionally, failing to review work after calculations can result in simple arithmetic errors or misinterpretations of the results.

Frequent Errors to Avoid

Misreading the Problem: Not fully understanding what is being asked can lead to wrong solutions. Always take time to analyze the question carefully.
Ignoring Units: Forgetting to keep track of units during calculations is a common mistake. Always ensure that units are consistent and properly handled.
Incorrect Formula Application: Using the wrong formula for a given problem is a frequent issue. Make sure to apply the correct equation based on the shape and the type of calculation.
Skipping Diagram Drawing: Not visualizing the problem can make it difficult to understand relationships between elements. Drawing a diagram helps in most cases.
Overlooking Properties: Forgetting important geometric properties, such as symmetry or the Pythagorean theorem, can lead to missing crucial steps in your solution.

How to Avoid These Mistakes

Take your time to read the problem carefully, ensuring you understand every detail.
Review your work at each stage, checking for any errors or omissions.
Always draw a diagram to help visualize the relationships between different elements.
Ensure that the correct formulas are being used, and remember to check units when necessary.

By being aware of these common mistakes and following a systematic approach, you can avoid these pitfalls and solve problems with greater accuracy and confidence.

Important Theorems for Geometry 1.3

Theorems form the foundation of mathematical reasoning, providing essential tools for solving complex problems. In this section, we will explore key theorems that are frequently applied to problems involving shapes, angles, and measurements. Understanding these principles will allow you to approach tasks with a clearer strategy and greater precision.

One of the most fundamental principles is the Pythagorean Theorem, which relates the sides of a right triangle. This theorem is essential when solving problems involving distances or finding missing side lengths in right-angled figures. Similarly, the Triangle Sum Theorem states that the sum of the angles in any triangle is always 180 degrees, a crucial rule for solving angle-related problems.

Congruence and similarity theorems are also pivotal in many problems. The SSS (Side-Side-Side) Congruence Theorem allows us to determine that two triangles are congruent if their corresponding sides are equal. Likewise, the AA (Angle-Angle) Similarity Theorem helps establish the similarity between triangles when two angles are congruent.

Understanding these theorems–and knowing when and how to apply them–greatly enhances your ability to solve geometric problems efficiently and accurately. With practice, these principles become second nature and serve as powerful tools for a variety of tasks.

Geometry 1.3 Answer Strategies

Effective problem-solving relies on applying the right strategies and techniques to arrive at a correct solution. In this section, we will explore various methods to approach mathematical challenges systematically. These strategies are designed to improve efficiency and accuracy, helping you handle tasks with greater confidence.

Key Approaches to Solving Problems

Break Down the Problem: Start by identifying the known information and what needs to be determined. Understanding the problem’s structure makes it easier to select the correct tools and formulas.
Draw Diagrams: Visualizing the situation by sketching a diagram can clarify the relationships between the elements, making the problem more manageable.
Use Logical Steps: Follow a logical sequence of operations, applying known theorems and formulas at each step. This helps avoid confusion and reduces the likelihood of errors.
Check for Special Conditions: Look for any unique properties or relationships, such as parallel lines, perpendicularity, or symmetry, which may simplify the problem.

Verification and Refinement

After solving, double-check your calculations and ensure the results make sense in the context of the problem.
If the answer seems incorrect, revisit earlier steps to identify potential mistakes or missed information.
Try solving the problem using an alternative method or approach to verify the correctness of your solution.

By incorporating these strategies into your approach, you can tackle even the most challenging problems with a more structured and methodical mindset, leading to more accurate and reliable solutions.

Visualizing Geometry Problems Effectively

One of the most powerful techniques in solving mathematical challenges is visualizing the problem. By creating a mental or physical image of the situation, you can better understand the relationships between different elements and identify the most efficient path to a solution. This method helps transform abstract concepts into tangible ones, making complex tasks more manageable.

When tackling a problem, the first step is to sketch a diagram. Even a simple drawing can reveal important information, such as angles, distances, and symmetries, that might not be immediately obvious from the problem statement alone. A clear visual representation not only aids in comprehension but also helps in organizing and structuring the solution process.

Tips for Effective Visualization

Tip	Description
Draw to Scale	Whenever possible, draw a diagram to scale, ensuring that the proportions and distances are accurate. This will help prevent misunderstandings of the problem’s dimensions.
Label Key Elements	Mark all important points, lines, and angles in your diagram. Proper labeling makes it easier to identify relationships and track what has been calculated.
Use Different Colors	Using different colors for different elements can help distinguish between various parts of the figure, such as different lines, angles, and shapes.
Highlight Symmetry	If the figure has symmetry, highlight it. Symmetry often simplifies the problem and can lead to quicker insights.

By visualizing the problem clearly and organizing the information in a diagram, you increase the likelihood of spotting critical details and relationships. This method also reduces the chance of overlooking important facts and improves your ability to apply the correct methods for a solution.

Practical Tips for Geometry Success

Mastering mathematical problems requires not only understanding concepts but also applying them effectively in various situations. Success in these types of tasks depends on developing strong strategies, maintaining focus, and consistently practicing essential skills. This section offers practical tips to help you navigate through challenges with greater confidence and efficiency.

Building a Strong Foundation

Understand the Basics: Ensure that you have a solid grasp of fundamental principles. Knowing core concepts allows you to build on them and solve more complex problems.
Practice Regularly: The more problems you solve, the better you become. Consistent practice helps you recognize patterns and reinforces your problem-solving abilities.
Ask Questions: If you’re unsure about a specific concept or step, don’t hesitate to ask for clarification. Seeking help ensures that you don’t get stuck on difficult problems.

Effective Problem-Solving Techniques

Break the Problem Into Steps: Divide the task into smaller, more manageable parts. This prevents you from feeling overwhelmed and allows you to focus on one element at a time.
Double-Check Your Work: After completing a problem, take a moment to review your solution. This can help you catch simple mistakes and ensure accuracy in your final answer.
Use Visual Aids: Whenever possible, draw diagrams or make sketches. Visualizing the problem can clarify relationships between elements and simplify the solution process.

By integrating these strategies into your study habits and problem-solving process, you can significantly improve your performance and achieve success with greater ease. With continued practice and persistence, you’ll develop the skills needed to tackle even the most challenging tasks.

Breaking Down Complex Solutions

Solving intricate mathematical problems can often seem daunting, but the key to tackling them successfully lies in breaking the solution into smaller, more manageable steps. By isolating each component and applying the right strategies, even the most complicated problems can become easier to understand and solve. This approach allows for greater clarity and minimizes the chances of overlooking critical details.

Step-by-Step Approach

Start by analyzing the problem and identifying all known and unknown elements. Organizing the given information is essential for understanding how the pieces of the puzzle fit together. Once you have a clear picture, break the problem down into smaller tasks, solving one piece at a time. This method helps prevent feeling overwhelmed and ensures that no important details are missed.

Identify Key Relationships: Look for patterns, such as parallel lines, perpendicularity, or symmetry. These properties often provide shortcuts for solving problems.
Apply Known Theorems: Use established principles and formulas to simplify the problem. Whether it’s a well-known rule or a specific strategy, these tools can help speed up the process.
Recheck Your Work: After solving each part of the problem, revisit your steps to ensure that you’ve accounted for all variables. Double-checking reduces the likelihood of making mistakes in later steps.

Using Visual Aids

Whenever possible, create diagrams to visually represent the problem. A clear diagram can help you see the relationships between different elements, such as angles, distances, or intersections. This visual representation often makes the solution process smoother and more intuitive. Label the diagram carefully to track each step and keep track of your progress.

By following these methods, complex problems become more structured, and the solution process becomes less overwhelming. With each step, you’ll gain a deeper understanding of the task at hand and ultimately find a more efficient path to the solution.

Key Formulas for Geometry

In the study of shapes, angles, and spaces, formulas play a crucial role in solving problems efficiently. These mathematical expressions allow you to calculate key properties such as area, volume, distance, and angles, forming the foundation for tackling a wide range of challenges. Understanding and memorizing these formulas is essential for success, as they streamline the solution process and provide reliable methods for achieving accurate results.

Area and Perimeter Formulas

To solve problems involving the size and boundaries of different shapes, it is essential to understand the following formulas:

Rectangle: Area = length × width; Perimeter = 2(length + width)
Triangle: Area = 1/2 × base × height; Perimeter = sum of all three sides
Circle: Area = π × radius²; Circumference = 2π × radius

Volume and Surface Area Formulas

For three-dimensional shapes, knowing how to calculate their volume and surface area is essential:

Cube: Volume = side³; Surface Area = 6 × side²
Cylinder: Volume = π × radius² × height; Surface Area = 2π × radius × (radius + height)
Sphere: Volume = 4/3 × π × radius³; Surface Area = 4π × radius²

By memorizing these key formulas, you gain the ability to quickly solve problems related to size, space, and boundaries, whether you’re working with two-dimensional or three-dimensional figures. Practicing their application in various problems will help solidify your understanding and ensure that you can confidently apply them in real-world scenarios.

How to Verify Your Solutions

Verifying your solutions is a critical step in the problem-solving process. It ensures that the calculations and logic used are correct and that the final result is valid. Taking the time to check your work not only helps prevent errors but also improves your understanding of the underlying concepts. This section provides effective methods to double-check your solutions and confirm their accuracy.

The first step in verification is to review the problem thoroughly. Ensure that you have interpreted all given information correctly and that no details have been overlooked. Next, retrace your steps and check each calculation, one by one. Often, simply reviewing the steps helps identify mistakes before they become major issues.

Another useful technique is to use a different method to solve the same problem. For example, if you’ve solved an equation algebraically, try solving it graphically or using a different formula. If both methods yield the same result, it’s likely that your solution is correct.

Finally, it is helpful to cross-check your final answer with the expected range or limits of the problem. If the solution falls within the reasonable range or adheres to the problem’s conditions, this adds confidence to the correctness of your answer. Conversely, if the result seems out of place, revisit your calculations and reasoning.

By consistently following these verification steps, you can ensure the reliability of your solutions and improve your problem-solving accuracy in the future.

Understanding Diagrams in Mathematics

Diagrams are essential tools for visualizing and solving problems in the study of shapes and spaces. They provide a clear representation of the problem, helping to identify relationships, angles, and dimensions. By interpreting diagrams correctly, you can often simplify complex problems and develop a deeper understanding of the underlying concepts.

Interpreting Diagrams Effectively

When approaching a diagram, it’s important to focus on key details and understand how they relate to the given problem. Here are a few tips to help you interpret diagrams accurately:

Look for labels: Pay attention to any labeled points, lines, and angles. These labels often provide critical information needed for solving the problem.
Identify symmetry: Recognizing symmetrical patterns can help simplify your calculations and lead to faster solutions.
Understand relationships: Diagrams often illustrate the relationships between different geometric elements, such as parallel lines, perpendicularity, or congruence.

Using Diagrams to Solve Problems

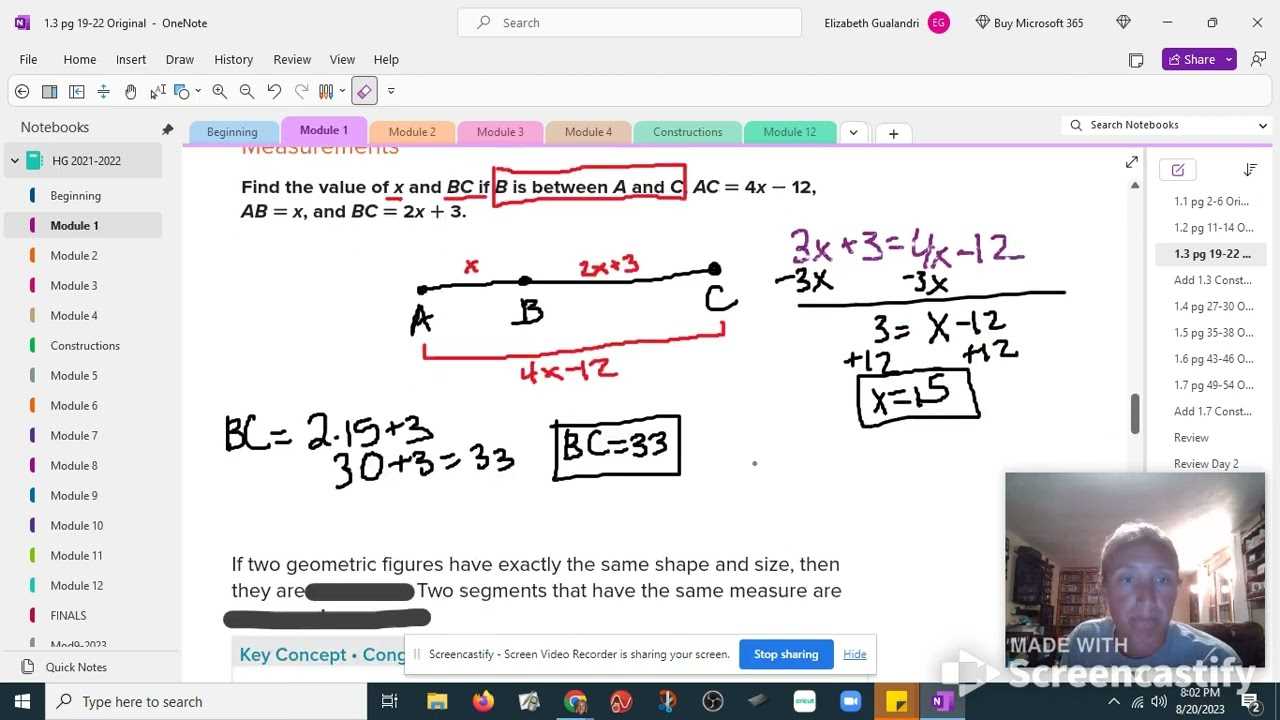
Once you’ve understood the diagram, use it to guide your problem-solving process. Consider the following strategies:

Apply known formulas: Many problems can be solved by applying geometric formulas directly to the diagram, such as calculating areas, angles, or distances.
Use visual cues: Diagrams often provide clues about the properties of shapes, such as right angles or equal sides, which can help determine missing values.
Break down complex diagrams: For more complicated problems, divide the diagram into smaller, more manageable sections to focus on one part at a time.

By carefully analyzing and interpreting diagrams, you can enhance your problem-solving skills and gain a clearer understanding of mathematical concepts.

Common Question Types in Mathematics

In the study of shapes, sizes, and spatial relationships, certain types of questions frequently appear. Understanding the common question formats can help you prepare effectively and approach problems with a clear strategy. These questions often test your ability to apply fundamental concepts and solve complex problems through various techniques.

Frequently Encountered Question Types

Here are some of the most common types of problems you might encounter:

Area and Perimeter Calculations: These questions require you to calculate the area or perimeter of different shapes, such as triangles, rectangles, and circles, using the appropriate formulas.
Angle Measurement: Problems that ask for the measurement of unknown angles often involve the use of geometric properties like complementary or supplementary angles, vertical angles, or parallel lines.
Properties of Shapes: These questions test your knowledge of the properties of various shapes, such as symmetry, congruency, or similarity, and how those properties affect the relationships within the figure.
Coordinate Geometry: These problems involve plotting points on a coordinate plane and applying the distance and midpoint formulas, or finding the equation of a line based on given points.
3D Shapes: Problems involving three-dimensional shapes require you to calculate volume, surface area, or other properties based on the shape’s dimensions.

Strategy for Tackling Common Question Types

To approach these types of problems effectively, here are a few strategies to keep in mind:

Break down the problem: Start by carefully reading the question and identifying the key information. Draw diagrams or label the given data to organize your thoughts.
Use appropriate formulas: For area, perimeter, and volume questions, make sure you’re using the correct formulas. Be sure to substitute values accurately.
Check for missing information: If some information is missing, look for clues in the problem that may help you derive the unknown values. Sometimes, additional geometric properties can help fill in the gaps.

By recognizing these common question types and applying the appropriate strategies, you can solve problems more efficiently and with greater confidence.

Improving Problem-Solving Skills

Developing effective problem-solving techniques is essential for mastering concepts related to shapes, sizes, and spatial relationships. The key to success lies in building a strong foundation, applying logical reasoning, and refining strategies through consistent practice. Whether you’re working on basic or complex problems, enhancing your ability to analyze and solve challenges will make a significant difference.

Key Techniques for Better Problem-Solving

To improve your problem-solving capabilities, consider adopting the following methods:

Practice Regularly: The more problems you tackle, the better you’ll understand the underlying concepts. Start with simple questions and gradually increase the difficulty level as you progress.
Draw Diagrams: Visualizing the problem can often make it easier to identify patterns and relationships. Sketch out shapes or structures and label key elements to help clarify your approach.
Break Down the Problem: Divide complex problems into smaller, more manageable parts. Solving simpler components individually often leads to a clearer overall solution.
Use Logical Reasoning: Approach each problem methodically. Use deductive reasoning to draw conclusions and solve unknowns based on known information.

Strategies for Effective Learning

In addition to practicing specific problems, it’s important to develop a well-rounded approach to learning that emphasizes understanding and retention:

Master Core Concepts: Ensure you fully understand the foundational principles before moving on to more advanced topics. This will help you solve problems more efficiently and with greater accuracy.
Learn from Mistakes: When you make errors, take the time to analyze what went wrong and why. This reflection will prevent similar mistakes in the future and strengthen your problem-solving skills.
Seek Additional Resources: If you’re stuck, look for alternative learning resources such as videos, textbooks, or study groups. Sometimes a different explanation can offer a fresh perspective.

Progress Tracking: Measuring Improvement

To monitor your progress and pinpoint areas that need more focus, consider using a tracking system. This could include keeping a log of the problems you’ve solved, the strategies you’ve used, and the time spent on each. Here’s an example:

Problem Type	Difficulty Level	Time Taken	Success Rate
Area Calculations	Medium	15 minutes	85%
Angle Measurement	Easy	10 minutes	95%
Coordinate Geometry	Hard	25 minutes	70%

By consistently using these strategies and tracking your progress, you’ll build confidence in your problem-solving skills and make noticeable improvements over time.

Practice Problems and Solutions

Practicing various types of problems is crucial for developing a deep understanding of spatial reasoning and mathematical relationships. By solving a range of questions, you can apply theoretical concepts to practical scenarios, enhancing your ability to solve real-world challenges. This section provides a collection of problems and their solutions to help reinforce key concepts and improve problem-solving techniques.

Problem Set 1: Area and Perimeter

In this section, we will focus on calculating the area and perimeter of different shapes. These problems require an understanding of formulas and the ability to apply them accurately.

Problem 1: Calculate the area of a rectangle with a length of 8 cm and a width of 5 cm.
Problem 2: Find the perimeter of a triangle with sides measuring 6 cm, 8 cm, and 10 cm.
Problem 3: A circle has a radius of 4 cm. What is its area?

Solutions to Problem Set 1

Solution to Problem 1: Area = Length × Width = 8 cm × 5 cm = 40 cm²
Solution to Problem 2: Perimeter = Sum of all sides = 6 cm + 8 cm + 10 cm = 24 cm
Solution to Problem 3: Area = π × radius² = π × 4² = 16π ≈ 50.24 cm²

Problem Set 2: Angles and Triangles

This set of problems focuses on the relationships between angles in triangles and other polygons. Understanding angle properties is essential for solving these questions.

Problem 1: In a right triangle, one angle measures 30°. What is the measure of the other non-right angle?
Problem 2: Calculate the interior angle of a regular pentagon.
Problem 3: Two angles of a triangle measure 40° and 60°. What is the measure of the third angle?

Solutions to Problem Set 2

Solution to Problem 1: The sum of angles in a triangle is 180°. Since one angle is 90° (right angle), the other two must add up to 90°. Therefore, the other angle is 60°.
Solution to Problem 2: The formula for the interior angle of a regular polygon is (n – 2) × 180° / n, where n is the number of sides. For a pentagon (n = 5), the interior angle is (5 – 2) × 180° / 5 = 540° / 5 = 108°.
Solution to Problem 3: The sum of the angles in any triangle is 180°. Since two angles measure 40° and 60°, the third angle is 180° – 40° – 60° = 80°.

By working through these practice problems, you’ll reinforce your understanding of key concepts and sharpen your problem-solving skills. Repetition is key to mastery, so be sure to practice regularly and tackle progressively harder problems to challenge yourself further.

Mastering Concepts Efficiently

Understanding the underlying principles of mathematical reasoning is essential for solving spatial problems effectively. By approaching each topic systematically and focusing on core concepts, you can improve your comprehension and application of key ideas. The key to mastering complex topics lies in practicing consistently and refining your approach through various techniques.

Step-by-Step Approach to Mastery

To fully grasp important concepts, break down each topic into manageable steps. Start by reviewing foundational material and progressively tackle more complex problems. This method ensures that you build a solid understanding and are able to apply principles confidently when facing challenges.

Step 1: Understand the basic definitions and theorems that form the foundation of the subject.
Step 2: Practice applying these definitions to solve simple problems and gradually increase the complexity.
Step 3: Analyze mistakes to identify gaps in knowledge and refine your techniques accordingly.

Using Visualization and Tools

One of the most effective ways to enhance understanding is through visual representation. Drawing diagrams or using digital tools can provide clarity and reveal relationships between different elements. By visualizing a problem, you can make abstract concepts more concrete and easier to manipulate.

Tip 1: Sketch diagrams to represent problems geometrically, which will help clarify spatial relationships.
Tip 2: Use online tools or graphing software to interact with dynamic visualizations, allowing for a deeper exploration of the material.

By following these steps and utilizing visualization tools, you can effectively master complex topics, deepen your understanding, and tackle problems with confidence. Consistent practice, combined with strategic learning methods, will set the stage for long-term success.