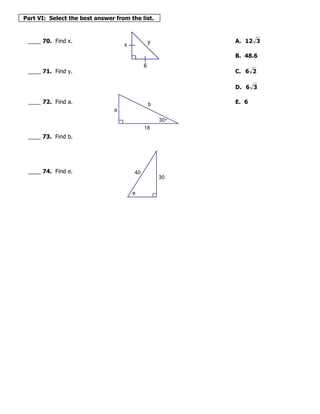
Preparing for a challenging assessment in mathematics requires a solid understanding of essential concepts and problem-solving techniques. Whether it’s solving complex equations, interpreting figures, or applying critical principles, the ability to navigate these tasks with precision is crucial for achieving top results.
Success in these evaluations comes down to knowing how to break down questions, use formulas effectively, and avoid common pitfalls. By focusing on core principles and practicing specific skills, you can build confidence and approach each problem with clarity.
Strategic preparation is the key to tackling various problem types, from simple calculations to intricate reasoning tasks. Familiarity with the material, paired with smart test-taking strategies, will help you perform at your best when it matters most.
Stay focused, stay prepared, and let your hard work shine through in your results.
Geometry Final Exam Answers
Understanding the key methods and techniques for solving mathematical problems is essential for mastering an assessment that tests your ability to apply various principles. This section covers the types of questions you may encounter and the approaches to handling them effectively. By breaking down the common topics, you will gain insight into how to approach each task with confidence and accuracy.
Below is a table summarizing some common problem types along with their corresponding strategies. These will guide you in solving challenges during the assessment and help ensure you apply the correct formulas and reasoning.
| Problem Type | Strategy | Example Approach |
|---|---|---|
| Angle Relationships | Use geometric properties to determine angle measures. | Identify complementary and supplementary angles, apply the sum of angles in polygons. |
| Area and Perimeter | Apply specific formulas for different shapes. | For rectangles, use length × width for area, and sum of sides for perimeter. |
| Volume and Surface Area | Use volume and surface area formulas for 3D figures. | For a cylinder, use πr²h for volume, and 2πr² + 2πrh for surface area. |
| Coordinate Geometry | Apply distance and midpoint formulas for points on a plane. | Use the distance formula √((x₂ – x₁)² + (y₂ – y₁)²) to find the distance between two points. |
By understanding these strategies and practicing them, you will be better prepared to tackle a variety of challenges with accuracy and speed. The key to success lies in being well-versed in these concepts and knowing how to apply them correctly under time constraints.
Key Concepts to Review Before Exam
To achieve success in any mathematical assessment, it is essential to have a strong grasp of the core principles that underpin problem-solving techniques. Focusing on these fundamental concepts will allow you to approach any challenge with confidence and efficiency. Below is a list of crucial topics that should be reviewed thoroughly before the assessment.
- Basic Shape Properties: Understand the characteristics of common shapes, including triangles, quadrilaterals, circles, and polygons.
- Measurement Formulas: Familiarize yourself with the formulas for calculating area, perimeter, volume, and surface area of various figures.
- Angle Relationships: Be comfortable with complementary, supplementary, and vertical angles, as well as the angle sum of polygons.
- Coordinate Systems: Practice working with points, lines, and slopes on the coordinate plane. Understand how to find distances and midpoints.
- Trigonometry: Review the sine, cosine, and tangent ratios and how to apply them in right-angled triangles.
- Geometric Proofs: Refresh your understanding of logical reasoning and how to construct formal proofs to justify geometric relationships.
By reviewing these topics, you will be well-prepared to tackle a wide range of problems effectively. Solidifying these key concepts ensures that you approach each question with the right tools and mindset, leading to better performance and greater accuracy under pressure.
Understanding Geometric Proofs and Theorems
Mastering the art of logical reasoning and applying established principles is key to solving complex mathematical problems. In this section, we will explore the importance of proofs and theorems, which serve as the foundation for justifying relationships between different figures and their properties. A solid understanding of these concepts will help you demonstrate your knowledge and approach problems with confidence.
Geometric proofs rely on deductive reasoning, where you start with known facts and build towards a conclusion through a series of logical steps. These steps are grounded in previously established theorems and postulates. By following a structured approach, you can justify each decision and arrive at accurate conclusions.
Key theorems to review include the Pythagorean Theorem, the properties of parallel lines, and angle relationships in polygons. These serve as essential tools for proving new relationships or solving problems. Understanding how to apply these principles effectively is crucial for performing well on any assessment.
By practicing proof construction and familiarizing yourself with essential theorems, you will be better equipped to handle a variety of tasks that require logical reasoning and a deep understanding of geometric relationships.
How to Solve Geometric Equations
Solving mathematical equations involving shapes and their properties requires a clear understanding of relevant formulas and the logical steps to apply them. Whether you’re dealing with areas, perimeters, or volume, knowing the right approach can make all the difference in reaching the correct solution. This section will guide you through the process of solving various types of geometric equations with confidence.
The first step in solving these types of problems is to carefully identify the quantities provided and the unknowns you need to solve for. Once the variables are understood, select the appropriate formula based on the figure in question. For example, to calculate the area of a rectangle, you would use the formula Area = Length × Width, while for the volume of a cylinder, you would use Volume = πr²h.
Next, ensure that all units are consistent, and substitute the known values into the equation. Simplify the expression step by step, following the correct order of operations. This careful approach will help you avoid errors and arrive at the correct result efficiently.
With practice, solving equations involving shapes becomes more intuitive, and you’ll be able to tackle even the more complex problems with ease. The key is to stay organized, apply formulas accurately, and double-check your work as you go.
Common Mistakes in Geometry Exams
During any mathematical assessment, it’s easy to make small errors that can lead to incorrect results. Understanding where mistakes typically occur can help you avoid them and perform better. This section highlights the most common pitfalls students face and provides tips on how to avoid them.
Misunderstanding Problem Requirements
One of the most frequent mistakes is failing to properly understand the question. Often, students overlook important details or misinterpret what is being asked, leading them to solve the wrong problem. Always take the time to carefully read each question, underline key terms, and ensure you understand what is being asked before proceeding with any calculations.
Incorrect Application of Formulas
Another common error is using the wrong formula or applying it incorrectly. This happens when students are not familiar with the specific formulas required for different shapes and figures. It’s crucial to memorize the formulas and understand when and how to use them. Double-check your work and ensure that you have selected the right formula for the problem at hand.
Pay attention to units as well, as mixing up different units (such as using square units when the problem asks for linear measurements) can also lead to mistakes. Always convert units when necessary to avoid these errors.
With practice and careful attention to detail, you can reduce the likelihood of making these common mistakes and improve your overall performance.
Tips for Mastering Geometry Formulas
Mastering the formulas used in mathematical problem solving is essential for success in any assessment. These formulas serve as powerful tools that allow you to calculate properties such as area, volume, and perimeter of various shapes. Understanding when and how to apply them is crucial for arriving at correct results quickly and efficiently.
Practice and Repetition
The best way to solidify your knowledge of mathematical formulas is through consistent practice. Write down the most important formulas, review them regularly, and solve as many practice problems as you can. Repetition helps commit these formulas to memory and improves your ability to recall them under time pressure.
Understand the Concept Behind Each Formula
Simply memorizing formulas is not enough. It’s important to understand the logic behind each formula so that you can apply it correctly in different contexts. For example, knowing why the area of a triangle is calculated using Area = 1/2 × base × height helps you understand its application to different types of triangles. Understanding the reasoning behind the formulas ensures you won’t make mistakes due to misapplication.
Visualize the Formulas: Drawing diagrams or using models can help you visualize how the formulas relate to the shapes you’re working with. This makes it easier to recall and apply them when needed.
With regular practice and a deeper understanding of the formulas, you’ll be able to handle even the most complex problems with ease.
Trigonometric Ratios in Geometry Exams
Trigonometric ratios are essential tools for solving problems involving right-angled triangles. These ratios, which relate the sides of a triangle to its angles, are fundamental in determining unknown lengths or angles in geometric figures. Mastering these ratios is crucial for accurately solving problems in any mathematical assessment.
The primary trigonometric ratios you need to focus on are sine, cosine, and tangent. Each ratio relates an angle to two specific sides of a right triangle. For example, the sine of an angle is the ratio of the opposite side to the hypotenuse, while the cosine relates the adjacent side to the hypotenuse, and the tangent compares the opposite side to the adjacent side.
Key Formulae:
- Sine (sin θ) = Opposite / Hypotenuse
- Cosine (cos θ) = Adjacent / Hypotenuse
- Tangent (tan θ) = Opposite / Adjacent
Understanding how to apply these ratios in different scenarios is crucial. For instance, if you’re given one side length and an angle in a right-angled triangle, you can use the appropriate ratio to find the other sides. With practice, you’ll gain the ability to quickly recognize which ratio to use and solve problems with confidence.
Geometry Strategies for Time Management
Effective time management is crucial when tackling mathematical problems, especially under time constraints. Developing strategies to manage your time wisely will help you approach each problem with confidence and accuracy. By organizing your time and prioritizing tasks, you can avoid feeling rushed and ensure that every question gets the attention it deserves.
Prioritize and Tackle Easier Problems First
One of the most effective ways to manage your time is by tackling the easier questions first. This allows you to gain momentum and ensures that you secure those points quickly. By solving the less complex problems early, you also free up time for the more challenging questions.
- Start with questions you are most comfortable with.
- Skip tough problems initially if they seem too time-consuming.
- Leave difficult questions for the end, once the easier ones are done.
Set Time Limits for Each Section

Another helpful technique is to allocate a specific amount of time to each section of the test. By setting time limits, you can prevent yourself from spending too much time on a single question. Stick to your time allocation to ensure you have enough time for every part of the assessment.
- Divide the total time by the number of sections or problems.
- Set a timer for each section to remind yourself when to move on.
- Don’t get stuck on one question; move on and return if needed.
By applying these strategies, you will improve your efficiency and ensure that you complete your tasks on time without sacrificing accuracy. Time management is a key skill that can make all the difference in a successful performance.
Preparing for Word Problems in Mathematics
Word problems are a common challenge in mathematical assessments, requiring you to translate real-world scenarios into solvable equations. These problems often involve multiple steps and can test both your comprehension and problem-solving abilities. To approach them successfully, it is important to follow a structured method that ensures accuracy and efficiency.
Break Down the Problem

The first step in solving any word problem is to carefully read and break down the information provided. Highlight or underline key details such as measurements, relationships between quantities, and what is being asked. This helps you understand the problem more clearly and guides you in determining what mathematical operations to use.
- Identify the variables: what are you solving for?
- Extract key numbers and relationships from the text.
- Understand the context–are you dealing with areas, volumes, or distances?
Set Up the Equation
Once you have a clear understanding of the problem, the next step is to translate the text into a mathematical equation. Use known formulas and relationships between the given values to set up the equation. Be mindful of units, ensuring consistency, and double-check that you’re solving for the correct unknown.
- Choose the right formula or method based on the problem type.
- Write down the equation clearly, ensuring all variables are defined.
- Solve step by step, checking your calculations as you go.
Practice is key when preparing for word problems. With each problem you solve, you’ll become more efficient at identifying the right approach and applying the correct formulas to reach a solution.
How to Tackle Coordinate Geometry

Coordinate-based problems are a fundamental aspect of many mathematical assessments. These problems involve working with points, lines, and shapes on a coordinate plane. To solve them effectively, it’s important to understand how to use the coordinates of various points to calculate distances, slopes, and other geometric properties. With a systematic approach, you can break down these problems into manageable steps.
Understanding the Coordinate Plane
The first step is to familiarize yourself with the basic concepts of the coordinate plane. The plane is divided into four quadrants by the x- and y-axes, where each point is represented by an ordered pair (x, y). The x-coordinate tells you how far a point is along the horizontal axis, while the y-coordinate indicates its position along the vertical axis. Understanding this layout is crucial for solving problems accurately.
- Plot points carefully on the graph.
- Identify the coordinates of points involved in the problem.
- Visualize the relationships between points, lines, and shapes on the plane.
Using Key Formulas
Once you have a clear understanding of the coordinate plane, you can apply various formulas to solve problems. Key formulas in coordinate-based problems include the distance formula, slope formula, and midpoint formula. These formulas allow you to find the distance between two points, the slope of a line, and the midpoint of a segment, which are essential for solving many types of problems.
- Distance Formula: d = √[(x₂ – x₁)² + (y₂ – y₁)²]
- Slope Formula: m = (y₂ – y₁) / (x₂ – x₁)
- Midpoint Formula: Midpoint = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)
By using these formulas, you can solve problems involving distances, angles, and shapes with ease. With consistent practice and attention to detail, you’ll be able to tackle these problems efficiently and accurately.
Understanding Circles and Their Properties
Circles are one of the most fundamental shapes in mathematics. They consist of all points that are equidistant from a central point, forming a perfect curve with unique properties. Understanding the key characteristics of circles and how to apply them is essential for solving related problems effectively. This section will explore the basic properties of circles and the essential formulas that come with them.
The Radius, Diameter, and Circumference
The three most important elements of a circle are the radius, diameter, and circumference. The radius is the distance from the center of the circle to any point on the boundary. The diameter is twice the length of the radius, passing through the center and connecting two points on the circle. The circumference is the total distance around the circle and can be calculated using the formula:
- Radius: The distance from the center to any point on the circle.
- Diameter: Twice the length of the radius, or d = 2r.
- Circumference: The total distance around the circle, calculated as C = 2πr.
Area of a Circle
Another crucial property is the area of a circle, which represents the space enclosed by the boundary. The area can be determined using the formula:
- Area: The space enclosed by the circle, calculated as A = πr².
By mastering these fundamental properties and formulas, you can solve problems involving circles with confidence and accuracy. Whether it’s finding the area, calculating the circumference, or working with the relationships between radius and diameter, these concepts are essential tools in geometry-related tasks.
Vocabulary Every Student Should Know
Mastering key terminology is essential for understanding mathematical concepts and solving problems effectively. Having a solid grasp of the language used in geometric reasoning will not only help with comprehension but also improve problem-solving skills. Below are some crucial terms that every student should be familiar with in order to excel in mathematics.
Basic Terms
There are several fundamental terms that serve as the building blocks for more advanced concepts. Understanding these will help students navigate through different topics with ease.
- Point: A specific location on a plane with no dimensions.
- Line: A straight path that extends infinitely in both directions.
- Angle: The space between two intersecting lines, measured in degrees.
- Plane: A flat surface that extends infinitely in all directions.
Shapes and Figures
Another essential category of terms involves various shapes and figures that are frequently encountered in mathematical problems.
- Circle: A set of points equidistant from a fixed point, called the center.
- Triangle: A polygon with three sides and three angles.
- Square: A quadrilateral with four equal sides and four right angles.
- Polygon: A closed figure with straight sides.
By familiarizing yourself with these terms, you will be better prepared to understand more complex ideas and apply them to solve problems. These definitions lay the foundation for building a deeper understanding of mathematical concepts and improving overall performance.
Applying Pythagorean Theorem in Problems
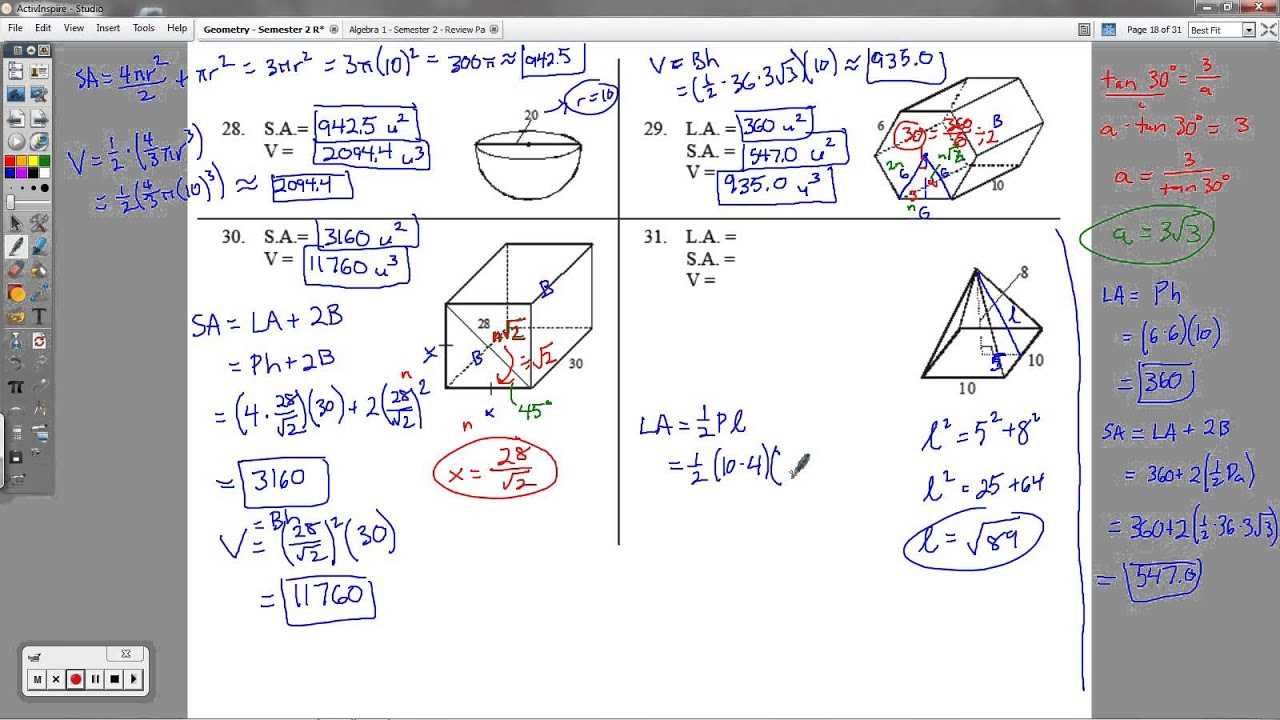
The Pythagorean Theorem is one of the most widely used principles in mathematics. It provides a simple yet powerful way to solve problems involving right-angled triangles. By applying this theorem, you can determine the length of any side of a right triangle when you have the lengths of the other two sides. Understanding how to use this concept is essential for solving a variety of practical and theoretical problems.
Understanding the Formula
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This is represented by the formula:
- a² + b² = c²
Here, a and b represent the lengths of the two legs, and c represents the length of the hypotenuse. By rearranging the formula, you can solve for any of the three unknowns if the other two are known.
Practical Applications
Applying the Pythagorean Theorem extends beyond theoretical problems and can be useful in real-world scenarios. Here are some examples of how it can be used:
- Distance Between Points: You can use the theorem to find the straight-line distance between two points on a coordinate plane.
- Finding Heights: When you have a right triangle and need to determine the height of an object, the theorem can help.
- Construction and Engineering: In construction, it’s used to verify that corners form right angles and for calculating distances in designs.
By consistently practicing the application of this formula, you will become proficient in solving a wide range of problems involving right-angled triangles.
Using Geometric Constructions Effectively

Geometric constructions are a crucial tool in mathematics, enabling students to visualize and solve problems with precision. These constructions involve creating figures with only a compass and straightedge, which help establish relationships between different elements in a shape. Understanding how to use these techniques effectively is essential for tackling many types of problems, from simple tasks like drawing perpendicular lines to more complex challenges like bisecting angles or creating equilateral triangles.
Basic Tools and Techniques
To begin using constructions, you need to be familiar with the essential tools and techniques involved in the process. The compass and straightedge are the two fundamental instruments required for drawing accurate constructions.
- Compass: Used to draw circles or arcs and measure distances between points.
- Straightedge: Used for drawing straight lines between two points without measuring the length.
These basic tools allow for a variety of constructions, including drawing perpendicular bisectors, angle bisectors, and circles with specific radii. Mastery of these foundational steps will enable you to approach more complex problems with confidence.
Common Constructions and Their Uses
Several key constructions form the foundation for problem-solving in geometric contexts. Below are some of the most commonly used methods:
- Perpendicular Bisector: This construction divides a line segment into two equal parts at a right angle. It is often used to find the midpoint of a segment or create a symmetry line.
- Angle Bisector: This method divides an angle into two equal parts, which is helpful for creating symmetric designs or finding unknown angle measures.
- Equilateral Triangle: Using a compass to construct an equilateral triangle allows you to create shapes with all sides equal, which is useful for various geometric proofs and designs.
By practicing these constructions, you will not only strengthen your problem-solving skills but also gain a deeper understanding of the relationships between shapes and their properties. Whether working on theoretical problems or real-world applications, mastering geometric constructions is an essential step in achieving success.
Handling 3D Geometry and Volume Calculations
When dealing with three-dimensional shapes, it’s essential to understand how to calculate their properties, particularly their volumes and surface areas. These calculations play a key role in various fields, including architecture, engineering, and physics. In this section, we will explore the key concepts involved in solving problems related to three-dimensional figures, focusing on the methods and formulas used to determine the volume and surface area of common solids.
Common 3D Shapes and Their Volume Formulas

To begin with, let’s review some of the most common three-dimensional shapes and their respective volume formulas:
- Cube: A cube has six equal square faces. The volume is calculated as side³, where “side” is the length of one edge of the cube.
- Cylinder: A cylinder consists of two parallel circular bases. The volume is given by π × radius² × height.
- Sphere: A sphere is a perfectly round shape. Its volume is calculated using the formula (4/3) × π × radius³.
- Pyramid: The volume of a pyramid is (1/3) × base area × height, where “base area” is the area of the pyramid’s base and “height” is the perpendicular distance from the base to the apex.
- Cone: A cone has a circular base and a pointed top. The volume is calculated as (1/3) × π × radius² × height.
By understanding and memorizing these formulas, you’ll be able to solve problems involving the volume of various solids with ease. The key is to recognize the shape, identify the required measurements, and apply the appropriate formula.
Surface Area of 3D Shapes
In addition to volume calculations, surface area is another important concept when working with three-dimensional figures. Surface area refers to the total area that covers the outside of a solid object. Each shape has its own specific formula for surface area:
- Cube: The surface area of a cube is 6 × side², where “side” is the length of one edge.
- Cylinder: The surface area is 2 × π × radius × height + 2 × π × radius², which includes both the lateral area and the areas of the two circular bases.
- Sphere: The surface area of a sphere is 4 × π × radius².
- Pyramid: To find the surface area, calculate the area of the base and add the areas of the triangular faces.
- Cone: The surface area is π × radius × (radius + slant height), which includes the lateral surface and the base area.
Mastering these formulas for volume and surface area will enable you to confidently tackle a wide range of problems related to three-dimensional objects. Whether you’re working on theoretical exercises or applying these concepts in practical scenarios, understanding how to handle 3D shapes is crucial for success.
How to Approach Angle and Triangle Questions
When solving problems related to angles and triangles, it’s essential to understand the fundamental relationships between the different types of angles and the properties of various triangle shapes. Recognizing key principles, such as the sum of angles in a triangle or the specific characteristics of right, acute, and obtuse angles, can significantly simplify these problems. The key to solving these questions is to break them down step by step, using known formulas and reasoning to find unknown values.
Start by identifying the type of triangle or angle involved in the problem. For instance, the sum of the interior angles in any triangle is always 180 degrees. If the problem involves a right triangle, remember that one angle is 90 degrees, and the other two must sum to 90 degrees. For triangles with unknown angles, you can use this basic principle to solve for the missing values.
In the case of angle relationships, be familiar with concepts such as complementary, supplementary, and vertically opposite angles. Complementary angles add up to 90 degrees, while supplementary angles sum to 180 degrees. Vertical angles, formed by two intersecting lines, are always equal. Recognizing these relationships will help you navigate more complex angle-based problems.
When solving for unknown sides or angles in a triangle, don’t forget to use the Pythagorean theorem for right triangles or trigonometric ratios such as sine, cosine, and tangent. These tools are essential for relating the sides and angles of right triangles and can help you solve a wide range of problems.
Lastly, always check your work by verifying that your results satisfy the conditions of the problem. This includes ensuring that the sum of the angles in a triangle equals 180 degrees or that the sides of a triangle adhere to the triangle inequality theorem, which states that the sum of the lengths of any two sides must be greater than the length of the third side.
Common Symbols and Their Meaning
In mathematical problems related to shapes and spatial relationships, specific symbols are used to represent various elements such as points, lines, angles, and distances. Understanding these symbols is crucial for interpreting the information correctly and solving problems effectively. Below is a list of commonly used symbols and their meanings in the context of geometric reasoning and problem-solving.
| Symbol | Meaning |
|---|---|
| ∅ | Empty set – represents the absence of elements in a set |
| ∧ | Intersection – represents the common elements between two sets or lines |
| ∨ | Union – represents the combined elements of two sets or lines |
| − | Minus sign – used to indicate subtraction or a difference between two quantities |
| = | Equals – indicates equality between two values or expressions |
| ⋅ | Dot product – used in vector mathematics to represent the product of two vectors |
| α, β, γ | Alpha, Beta, Gamma – commonly used to denote angles in geometric figures |
| ∫ | Integral – used to represent integration in calculus-based geometry problems |
| Δ | Delta – typically represents a change in a quantity or the difference between two values |
| < | Less than – used to indicate a value that is smaller than another |
| > | Greater than – used to indicate a value that is larger than another |
| − | Perpendicular – represents two lines that intersect at a right angle |
These symbols provide a universal language for representing different elements of mathematical problems. Familiarity with these symbols not only aids in understanding geometric concepts but also enhances your ability to work with mathematical equations and solve complex problems. Recognizing these symbols will help you navigate through problems with greater ease and precision.
How to Practice for Assessments
Effective preparation is key to performing well in any type of assessment. When it comes to spatial reasoning and figure-related challenges, consistent practice and a strategic approach can make a significant difference. The process involves understanding fundamental concepts, applying them in various contexts, and refining your problem-solving skills through continuous practice.
Start with the Basics: Before diving into complex problems, ensure you have a strong grasp of the foundational concepts. This includes understanding common terms, properties of shapes, and basic principles. Familiarize yourself with theorems, postulates, and formulas that form the basis of more advanced topics.
Practice with Different Types of Problems: It’s essential to practice with a wide variety of problem types. Work on both simple and complex questions to build your confidence and ability to tackle different scenarios. Start with straightforward problems, then gradually progress to more challenging ones.
Break Down Problems: When you encounter a difficult problem, break it into smaller, more manageable steps. Focus on understanding what is being asked and how the known information relates to the unknown. This helps you avoid feeling overwhelmed and ensures a logical approach to finding the solution.
Use Visual Aids: Diagrams, sketches, and graphs can be incredibly helpful in visualizing problems. Drawing figures, labeling important points, and highlighting key relationships can simplify complex tasks and make it easier to see patterns or solutions.
Review Mistakes: It’s important not just to focus on correct answers but also to analyze any mistakes. Understanding why a solution didn’t work is a powerful tool for improving. Take time to revisit incorrect answers and grasp the reasoning behind the correct ones.
Simulate Test Conditions: One effective way to practice is by setting up mock assessments that mimic actual conditions. Time yourself, avoid distractions, and solve problems under similar pressure. This will help improve your time management and ensure you’re prepared for the actual assessment environment.
By applying these strategies and regularly practicing, you’ll develop the necessary skills to approach problems with confidence and efficiency. With focused effort, you’ll be better equipped to excel and demonstrate your knowledge during the actual assessment.