
Preparing for a test involving shapes, angles, and spatial reasoning requires a solid understanding of key concepts and effective strategies. Mastery over the core principles allows students to approach each problem with confidence, ensuring they can apply the right methods to arrive at the correct solution. Whether the questions require calculation or logical deductions, a structured approach can make all the difference.
Critical thinking plays a major role in these assessments. With practice, one can quickly identify patterns and choose the most efficient problem-solving techniques. The more familiar you become with different types of questions, the easier it is to navigate the test and manage your time effectively. Whether it involves complex shapes or straightforward formulas, every question presents an opportunity to showcase your skills.
Preparation is the key to success. Regular practice, along with a deep understanding of the underlying principles, will help reduce errors and increase your speed. With the right tools and mindset, anyone can improve their performance in these mathematical challenges.
Geometry Exam Answers Guide
Successfully navigating through a test that involves shapes, measurements, and spatial reasoning requires a strategic approach. Mastery of essential concepts and efficient problem-solving techniques will ensure that each challenge is met with confidence and clarity. Developing an understanding of common question formats and practicing key skills are crucial for improving performance and accuracy.
Understanding the Core Concepts

Before tackling any questions, it’s important to have a solid grasp of the fundamental principles. Focus on understanding the relationships between different elements, such as lines, angles, and figures. Once the core concepts are clear, solving even the most complex problems becomes a matter of applying the right strategies. A systematic approach to breaking down each question is essential for success.
Effective Strategies for Solving Problems
When faced with various tasks, being able to quickly identify the type of problem and apply the appropriate technique is key. Whether it’s solving for unknown values or proving specific theorems, having a toolkit of methods–such as using known formulas or drawing accurate diagrams–helps simplify the process. Time management also plays a role; allocating enough time for each section while remaining calm and focused is vital for achieving the best result.
Key Concepts to Master for Geometry Exams
Achieving success in tests involving shapes, angles, and measurements requires a deep understanding of foundational principles. Mastering certain concepts not only enhances problem-solving abilities but also makes tackling even the most challenging questions more intuitive. Familiarity with core topics helps students quickly recognize patterns and apply the most efficient strategies to find solutions.
Understanding Shapes and Their Properties
One of the most important areas to focus on is the properties of different figures. Circles, triangles, and polygons each have unique characteristics that must be understood in depth. Recognizing these properties allows for easier calculation of areas, perimeters, and angles. Additionally, knowing the relationships between different shapes is essential for solving complex problems.
Angles and Their Relationships
Another critical concept is mastering the various types of angles and how they interact. From acute to obtuse and right angles, understanding their definitions and properties is fundamental for accurately solving problems involving lines, intersections, and parallelism. Being able to identify and apply the angle sum and angle bisector principles is essential for success.
Common Geometry Problems and Solutions
In any test involving shapes, measurements, and spatial reasoning, certain types of problems tend to appear more frequently. Recognizing these common challenges and knowing the appropriate methods to solve them can significantly improve your performance. By understanding how to tackle each type of problem, you can approach your tasks with confidence and efficiency.
Below are some of the most common types of problems and their solutions:
| Problem Type | Solution Method |
|---|---|
| Area of a Triangle | Use the formula: Area = 1/2 × base × height. |
| Finding the Length of a Side in a Right Triangle | Apply the Pythagorean Theorem: a² + b² = c². |
| Angle Sum of a Polygon | Use the formula: (n – 2) × 180°, where n is the number of sides. |
| Circumference of a Circle | Use the formula: Circumference = 2π × radius. |
| Volume of a Rectangular Prism | Use the formula: Volume = length × width × height. |
Familiarizing yourself with these problems and their solutions will help you handle various situations during the test and save time while ensuring accuracy. The key is to practice these types of problems regularly to increase both speed and confidence.
Step-by-Step Geometry Problem Solving
Breaking down complex tasks into smaller, manageable steps is crucial for solving problems effectively. By following a structured approach, you can ensure that each aspect of the problem is addressed systematically. Whether you are dealing with calculations or logical deductions, a clear process will help avoid mistakes and improve efficiency.
Step 1: Understand the Problem
The first step is to carefully read and analyze the problem. Ensure you understand what is being asked and identify the key information provided. Look for any specific requirements, such as measurements, relationships between shapes, or conditions to be met.
- Highlight important values, such as side lengths or angles.
- Note any relationships between different shapes or figures.
- Determine what you need to find or prove.
Step 2: Organize the Information
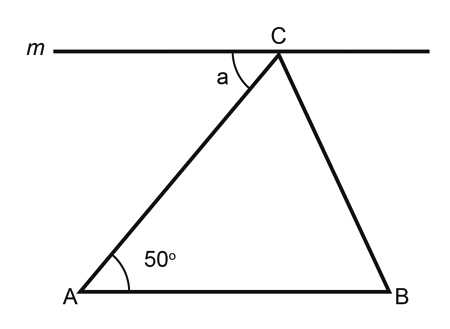
Once you have a clear understanding of the problem, the next step is to organize the given information. This will help you visualize the situation and identify the correct approach to solving the task.
- Draw a diagram to represent the problem visually.
- Label all known values and relationships on the diagram.
- Identify any missing information that you need to solve for.
Step 3: Apply the Right Method
Now that the problem is clearly defined and organized, you can begin solving it by applying the appropriate methods. Whether using formulas, theorems, or logical reasoning, ensure you are using the most efficient technique for the given situation.
- Use formulas to calculate areas, perimeters, or angles when needed.
- Apply known theorems, such as the Pythagorean theorem or angle sum properties.
- Check if there are any symmetry or proportionality properties that simplify the solution.
Step 4: Double-Check the Solution
Once you have arrived at an answer, it’s important to review your solution. Check all steps for accuracy and ensure that the answer makes sense within the context of the problem.
- Verify calculations to avoid simple mistakes.
- Ensure all steps logically follow from one another.
- Check if the solution meets the original problem’s requirements.
By following these steps, you can approach any problem with a structured and logical mindset, improving both your accuracy and efficiency.
How to Approach Geometry Test Questions
When facing a set of problems involving shapes, angles, and spatial reasoning, it’s important to have a clear strategy in place. Rather than rushing through each question, take the time to analyze and plan your approach carefully. By organizing your thoughts and breaking down each problem step by step, you increase your chances of finding the correct solution while minimizing errors.
First, read each question carefully and identify the key information. Look for specific measurements, relationships between figures, or any special instructions. Pay attention to terms like “parallel,” “perpendicular,” or “angle bisector,” as they often indicate the method you’ll need to apply. Understanding these terms early on will help you approach the problem with the right mindset.
Next, organize your thoughts. If necessary, draw a diagram or sketch of the situation. Label any known values, such as side lengths or angles, and make sure you understand the connections between different elements in the figure. Visualizing the problem is often the key to unlocking the correct approach.
When solving, choose the most efficient method based on the information provided. Use appropriate formulas, theorems, or logical reasoning to arrive at the solution. Remember, accuracy is crucial, so take your time with calculations and ensure you apply each step correctly.
Lastly, double-check your work. Once you’ve reached a solution, review all your steps to ensure no mistakes were made. If possible, verify your answer by substituting values back into any formulas or equations to see if they make sense within the context of the question.
By following this structured approach, you can tackle problems methodically and confidently, ensuring you maximize your chances of success on each question.
Geometry Formulas Every Student Should Know
Mastering key formulas is essential for solving various problems involving shapes, sizes, and measurements. Having these formulas at your fingertips allows for quicker problem solving and greater accuracy. Below are some of the most important equations every student should memorize and be comfortable applying.
Basic Formulas for Common Shapes
- Area of a Triangle: Area = 1/2 × base × height
- Area of a Rectangle: Area = length × width
- Area of a Circle: Area = π × radius²
- Perimeter of a Rectangle: Perimeter = 2 × (length + width)
- Perimeter of a Circle (Circumference): Circumference = 2π × radius
Formulas for Solid Figures
- Volume of a Rectangular Prism: Volume = length × width × height
- Volume of a Cylinder: Volume = π × radius² × height
- Surface Area of a Cube: Surface Area = 6 × side²
- Surface Area of a Sphere: Surface Area = 4π × radius²
Important Theorems and Relationships
- Pythagorean Theorem: a² + b² = c² (for right triangles)
- Angle Sum of a Triangle: The sum of all angles = 180°
- Angle Sum of a Polygon: (n – 2) × 180° (where n is the number of sides)
Familiarity with these key formulas will help streamline your problem-solving process and improve your overall efficiency in tackling related questions.
Tips for Quick Geometry Calculations
Speed and accuracy are crucial when working with measurements, angles, and various figures. Developing a set of strategies for quick calculations can help save valuable time during problem-solving. By mastering a few key tips, you can streamline your process and improve both your speed and precision.
One effective way to speed up calculations is to memorize essential formulas. Having these readily available means you won’t waste time looking them up or trying to recall them under pressure. Focus on the most commonly used equations, such as those for area, perimeter, and volume, and practice applying them quickly.
Another useful tip is to simplify complex problems by breaking them into smaller, more manageable steps. Start by identifying key measurements or properties of the figure, and then tackle one part of the problem at a time. This approach helps you stay organized and reduces the likelihood of making mistakes.
Additionally, look for shortcuts and patterns that can simplify your calculations. For instance, when calculating areas of certain shapes like squares or circles, you can quickly square the side length or multiply by π without needing to write out the full process. Recognizing such shortcuts helps improve your speed without compromising accuracy.
Lastly, practice mental math as much as possible. Being able to perform basic arithmetic in your head will save precious seconds when you encounter straightforward calculations. This is especially important for operations like multiplication, division, and working with fractions.
By integrating these tips into your study routine, you can handle problems with greater efficiency and confidence, ensuring faster and more accurate results.
Understanding Diagrams in Geometry Exams
Diagrams are crucial tools that help visualize and solve complex problems involving shapes, angles, and spatial relationships. They provide a visual representation of the problem, making it easier to identify key elements and apply the right methods. Properly interpreting these diagrams can significantly improve your understanding of the question and guide you to the correct solution.
How to Read Diagrams Effectively
When presented with a diagram, start by carefully analyzing the given figure. Label all known values such as lengths, angles, and any other relevant measurements. Often, these values are provided explicitly in the diagram or are derived from the problem’s description. Make sure you note any markings, such as right angles, parallel lines, or congruent sides, as they indicate important properties that can simplify your calculations.
Common Features to Look For
In many problems, certain features will appear consistently, providing you with useful clues. For example, parallel lines can suggest the use of specific angle theorems, while symmetry can lead to shortcuts in calculating areas or solving for unknown values. Perpendicular lines often indicate the need for right triangle properties or the Pythagorean theorem. Identifying these characteristics early on will help you determine the most effective approach to solving the problem.
By understanding the structure of diagrams and recognizing key elements, you can approach each question with a clearer strategy and solve problems more efficiently.
How to Improve Geometry Test Scores
Achieving higher scores in tests involving shapes, spatial reasoning, and measurements requires a combination of understanding key concepts, practicing regularly, and developing effective strategies. By focusing on essential skills and preparing systematically, you can significantly enhance your performance and boost your confidence when solving related problems.
First, solidify your understanding of core concepts. It’s essential to have a strong grasp of fundamental principles such as properties of figures, theorems, and formulas. Make sure you understand not only how to use these formulas but also why they work. This deeper understanding will help you apply them correctly in various scenarios.
Next, practice consistently. The more problems you solve, the more familiar you become with common problem types and techniques. Regular practice helps improve both speed and accuracy. Start with simpler problems to build confidence, then gradually move on to more challenging ones. This progression will ensure you are ready for any question you encounter.
Additionally, work on time management. During the test, it’s easy to get stuck on difficult questions. To avoid this, practice working under timed conditions. This will help you learn to allocate your time wisely, allowing you to answer easier questions first and come back to tougher ones if needed.
Review your mistakes after each practice session or test. Take note of areas where you struggled, and make sure to address these weaknesses in your studies. Understanding why you made mistakes and how to correct them is key to improving your overall performance.
Finally, stay organized during the test. Keep your work neat, label all measurements clearly, and show your steps when solving problems. This not only helps prevent errors but also makes it easier to double-check your work if time allows.
By consistently applying these strategies, you can improve your skills, increase your confidence, and achieve better results on your next test.
Geometry Practice Tests and Resources
To succeed in tests involving shapes, measurements, and spatial reasoning, consistent practice is essential. Utilizing the right resources can make a significant difference in mastering the skills required. A combination of practice tests and helpful study materials can help reinforce key concepts, identify areas for improvement, and enhance overall problem-solving abilities.
Top Practice Test Resources
- Online Quizzes and Practice Platforms: Many websites offer free practice tests tailored to different difficulty levels. These platforms provide instant feedback, helping you identify your strengths and weaknesses.
- Test Prep Books: Comprehensive study guides often include a wide range of practice problems with detailed solutions. These books are structured to help students understand problem-solving techniques step by step.
- Interactive Apps: Mobile apps designed for math practice can provide interactive exercises that test your knowledge and help improve your skills in a more engaging way.
Additional Study Resources
- Video Tutorials: Educational platforms like YouTube feature countless tutorials on specific topics, offering visual explanations of complex concepts.
- Study Groups: Joining a study group allows you to discuss problems, share insights, and tackle challenging questions together.
- Practice Worksheets: Printable worksheets are a great way to get extra practice with problems that align with what you’re studying in class.
By consistently practicing with these resources, you’ll develop a better understanding of key concepts and build confidence in solving various problems, ultimately improving your performance.
Time Management During Geometry Exams
Effective time management is a crucial skill when solving problems that involve shapes, measurements, and spatial reasoning. Without a clear strategy, it’s easy to get bogged down on difficult questions or rush through easier ones, ultimately affecting your overall performance. By learning how to allocate your time wisely, you can ensure that you have enough time to answer all questions accurately and thoroughly.
One key strategy is to quickly skim through the entire set of questions at the beginning. This allows you to gauge the difficulty of each problem and decide which ones to tackle first. Start with the questions you find easiest, as this will build momentum and give you more time for the more challenging ones later.
Another important tactic is to set time limits for each section or problem. For example, if a question seems time-consuming, give yourself a fixed amount of time to work through it. If you don’t arrive at a solution within that time frame, move on and return to it later if time allows. This prevents you from spending too much time on one problem while neglecting others.
Additionally, practice solving problems under timed conditions before the actual test. This will help you become more accustomed to pacing yourself and allow you to identify which types of questions tend to take up more time. It also helps you develop the ability to recognize patterns in problems, speeding up your thought process during the actual test.
Lastly, keep an eye on the clock during the test, but don’t obsess over it. Focus on solving problems, but check the time periodically to ensure you’re staying on track. This balance of focus and awareness will help you manage your time effectively and improve your chances of completing the test successfully.
Effective Study Techniques for Geometry
Mastering the principles of shapes, spatial reasoning, and measurement requires more than just memorization. The key to success lies in understanding the underlying concepts and applying them effectively to various problems. By using targeted study techniques, you can build a deeper comprehension and gain confidence in solving even the most challenging problems.
One effective study strategy is to focus on conceptual understanding. Instead of simply memorizing formulas, take the time to understand how and why they work. This will help you apply them correctly in different scenarios, whether you’re solving for angles or calculating areas.
Practice regularly with a variety of problems. Consistent practice helps reinforce what you’ve learned and allows you to become familiar with different types of questions. Start with basic exercises to solidify your understanding, and gradually move on to more complex problems. This progression helps you build problem-solving skills step by step.
Another effective technique is breaking down complex problems. If you come across a challenging question, break it down into smaller, more manageable parts. Solve each part systematically and then combine your results. This approach helps prevent overwhelm and ensures you tackle problems with confidence.
Visualization is also a powerful tool in mastering this subject. Drawing diagrams and labeling important information can help you better understand the problem and identify relationships between different elements. This method enhances spatial awareness and makes complex problems easier to solve.
Finally, review your mistakes and learn from them. After completing practice problems, revisit any mistakes to understand where you went wrong. This reflection helps reinforce your learning and ensures you avoid similar errors in the future.
Understanding Proofs in Geometry Tests
In subjects that involve shapes and spatial reasoning, proofs play a crucial role in demonstrating the validity of statements or solving problems logically. Understanding how to construct and present a proof is essential for success in these tests. A proof is essentially a series of logical steps that show why a particular statement is true based on established facts or previously proven theorems. Mastering this skill allows you to approach complex problems with confidence and clarity.
When working on proofs, it’s important to break down the problem into smaller, manageable steps. Start by identifying the given information and the statement that needs to be proven. From there, organize your reasoning in a clear, step-by-step manner, using definitions, postulates, and theorems that support your argument. Keep in mind that every statement in the proof must be justified, either by previously known facts or logical reasoning.
Here’s an example of how a proof might be structured:
| Step | Statement | Reason |
|---|---|---|
| 1 | Given: Triangle ABC, where AB = AC | Problem Statement |
| 2 | Angle ABC = Angle ACB | Isosceles Triangle Theorem |
| 3 | Triangle ABC is isosceles | By definition of an isosceles triangle |
| 4 | Conclusion: Angle ABC = Angle ACB | By properties of isosceles triangles |
In this example, each step logically follows from the previous one, and each statement is justified. Being thorough and methodical in your approach will help you stay organized and ensure that your proof is clear and convincing.
To further improve your skills, practice solving various proof problems. This will help you become familiar with different types of theorems and postulates, as well as develop a deeper understanding of how to construct a well-supported argument. Over time, these techniques will become second nature, making it easier to tackle complex questions during a test.
How to Avoid Common Geometry Mistakes
When tackling problems involving shapes, measurements, and spatial relationships, it’s easy to fall into common traps that can lead to mistakes. However, by being aware of these frequent errors, you can develop strategies to prevent them and approach each problem with greater accuracy. Careful attention to detail and following a systematic process will help ensure that you avoid missteps and enhance your problem-solving skills.
One of the most common errors is misinterpreting the problem. It’s essential to take the time to fully understand the given information before attempting to solve the question. Carefully read each part of the problem and highlight key details, such as dimensions or specific relationships between shapes. This helps prevent overlooking important facts that could affect your solution.
Forgetting to label important points or angles is another frequent mistake. Always draw clear diagrams and label them properly. This step is crucial because it allows you to visualize the problem and keeps track of the different elements involved. Without a labeled diagram, it becomes much harder to spot relationships between points, sides, or angles that may be essential for solving the problem.
Using the wrong formulas is another issue that can easily arise. Make sure you are familiar with the various formulas and their correct applications. For example, using the wrong formula for calculating area or perimeter can lead to incorrect results. Double-check which formula is relevant to the specific problem at hand, and ensure you’re applying it correctly. If in doubt, refer back to the fundamentals.
Finally, rushing through calculations is a mistake that many make under time pressure. While it’s tempting to move quickly through a problem, hasty calculations often lead to simple arithmetic errors. Always take your time with the math, double-check each step, and ensure that you’re not overlooking details. A small miscalculation can change the entire outcome of the problem.
By paying attention to these common pitfalls and practicing a methodical approach, you can reduce mistakes and improve your overall performance. Mastering these habits not only enhances your accuracy but also builds confidence, helping you tackle more complex problems with ease.
Question Types You Should Know
Understanding the various types of problems that may appear on a test is a critical part of effective preparation. Different question formats require different approaches, and knowing what to expect can help you strategize your responses more efficiently. In this section, we will explore common types of problems, how to recognize them, and tips for solving them.
1. Calculation-Based Problems
These questions often involve applying specific formulas to solve for missing values, such as lengths, areas, or volumes. They test your understanding of fundamental mathematical concepts and your ability to apply them accurately.
- Area calculations: Questions may ask you to calculate the area of various shapes, such as triangles, rectangles, or circles.
- Volume calculations: You may be asked to calculate the volume of 3D objects like cubes, spheres, or cylinders.
- Distance and length: These problems involve finding the distance between two points or the length of a segment using geometric properties.
2. Proof-Based Problems
In these types of problems, you are asked to prove a specific geometric property or relationship. These questions assess your understanding of theorems, postulates, and logical reasoning skills. The key to solving proof questions is to build a logical argument step by step.
- Proving triangles are congruent: Often, you may need to show that two triangles are congruent using criteria like side-angle-side (SAS) or angle-side-angle (ASA).
- Angle relationships: Proving angle relationships, such as vertical angles being equal or supplementary angles summing to 180 degrees, is a common proof question.
- Using theorems: You might be asked to apply well-known theorems, like the Pythagorean theorem, to prove other geometric relationships.
3. Word Problems and Applications
These problems require you to interpret real-world situations and apply geometric principles to solve them. They often include scenarios involving measurements, proportions, and spatial reasoning.
- Real-world contexts: You may be asked to solve problems involving architecture, design, or navigation that require applying geometric knowledge to practical situations.
- Proportions and scale: Some questions involve solving problems with scale models, such as finding the dimensions of an object based on a given ratio.
Recognizing the different types of questions and understanding the strategies needed to solve them will help you approach each problem with confidence and precision. Regular practice with these various question types will also ensure that you are well-prepared for any challenge that comes your way.
Strategies for Word Problems
Word problems are one of the most challenging aspects of any test. These questions require more than just applying formulas; they demand interpretation, analysis, and a structured approach to translate real-world scenarios into solvable problems. In this section, we will explore effective strategies to tackle these types of questions with confidence and accuracy.
1. Understand the Problem
The first step in solving a word problem is to carefully read and understand the scenario. Identify the key pieces of information and what the problem is asking you to find. Breaking down the text into manageable parts will allow you to focus on the relevant details without feeling overwhelmed.
- Highlight important information: Underline or note down the key values and relationships provided in the problem.
- Identify what’s unknown: Determine which values you need to solve for and what formulas or concepts apply to those unknowns.
2. Visualize the Problem
Once you have a clear understanding of the scenario, create a diagram or sketch to visualize the situation. Drawing out the problem can help make abstract concepts more tangible and can reveal hidden relationships between elements of the problem.
- Draw accurate diagrams: Label all known values and angles to help organize the information clearly.
- Mark unknowns: Clearly mark any unknown values or variables in the diagram to keep track of what you need to find.
3. Set Up an Equation
With a visual representation and a clear understanding of the problem, the next step is to set up an equation or system of equations based on the relationships identified. This is where your knowledge of formulas and theorems becomes crucial.
| Step | Action | Example |
|---|---|---|
| Identify relationships | Analyze the problem and determine how the known values are related to the unknowns. | If a triangle’s perimeter is given, and two sides are known, use the perimeter formula. |
| Set up equation | Use the identified relationships to set up an equation to solve for the unknowns. | Let x represent the third side, then solve for x using the perimeter formula. |
By organizing your thoughts, visualizing the situation, and setting up the right equation, you’ll be in a strong position to solve the problem correctly and efficiently.
Preparing for Advanced Questions
As you advance in your studies, the problems you encounter become increasingly complex, requiring a deeper understanding and more sophisticated problem-solving techniques. These higher-level challenges often test your ability to apply multiple concepts in a single question and demand both logical thinking and creativity. To excel in these types of problems, it is essential to have a systematic approach that prepares you for the variety of scenarios you may face.
1. Master the Fundamentals
Before tackling advanced problems, ensure that you have a solid grasp of the basic principles. Mastery of foundational concepts such as shapes, angles, ratios, and their properties forms the bedrock for solving more complicated problems. Without a thorough understanding of these building blocks, it will be difficult to progress to more intricate tasks.
- Review key formulas: Revisit essential equations and relationships to ensure they are firmly understood.
- Practice basic problems: Consistently work through simpler problems to reinforce core concepts and techniques.
2. Develop Problem-Solving Strategies
Advanced problems often require combining different strategies and concepts. Developing a variety of problem-solving techniques is crucial to successfully navigating more challenging questions. These may involve recognizing patterns, applying logical deductions, or using multiple approaches to reach the solution.
- Work through examples: Study worked-out solutions to learn how different techniques can be applied in real-world scenarios.
- Break down complex problems: When faced with a complicated problem, break it into smaller, manageable parts and solve each part step by step.
By focusing on strengthening your core knowledge and honing your problem-solving skills, you can approach advanced questions with confidence and efficiency, making even the most challenging problems more approachable.