Geometry Final Exam Review Packet Answers

Mastering key concepts and solving complex problems is crucial for achieving top results in any assessment. This section is designed to help you strengthen your understanding and boost your confidence through detailed explanations and well-organized examples. By focusing on core principles and strategies, you can improve your problem-solving skills and tackle various question types effectively.

In this guide, you’ll find clear and concise solutions to common challenges encountered in mathematical tasks. Whether you’re revisiting essential formulas, revising geometric properties, or learning how to apply logic to various scenarios, this material will provide valuable insights and techniques for success. From basic principles to advanced methods, this section covers everything you need to excel.

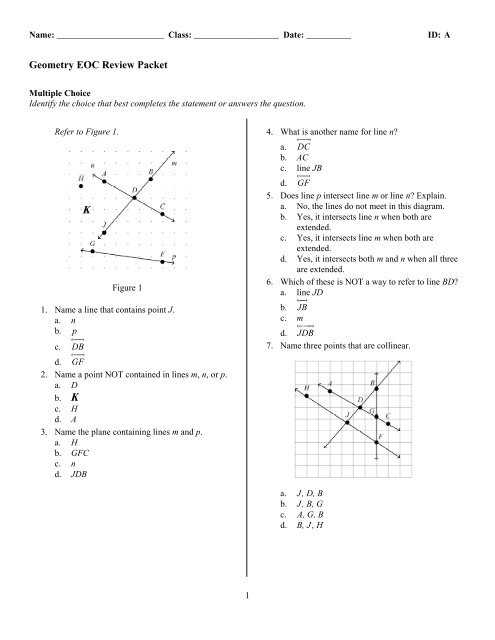
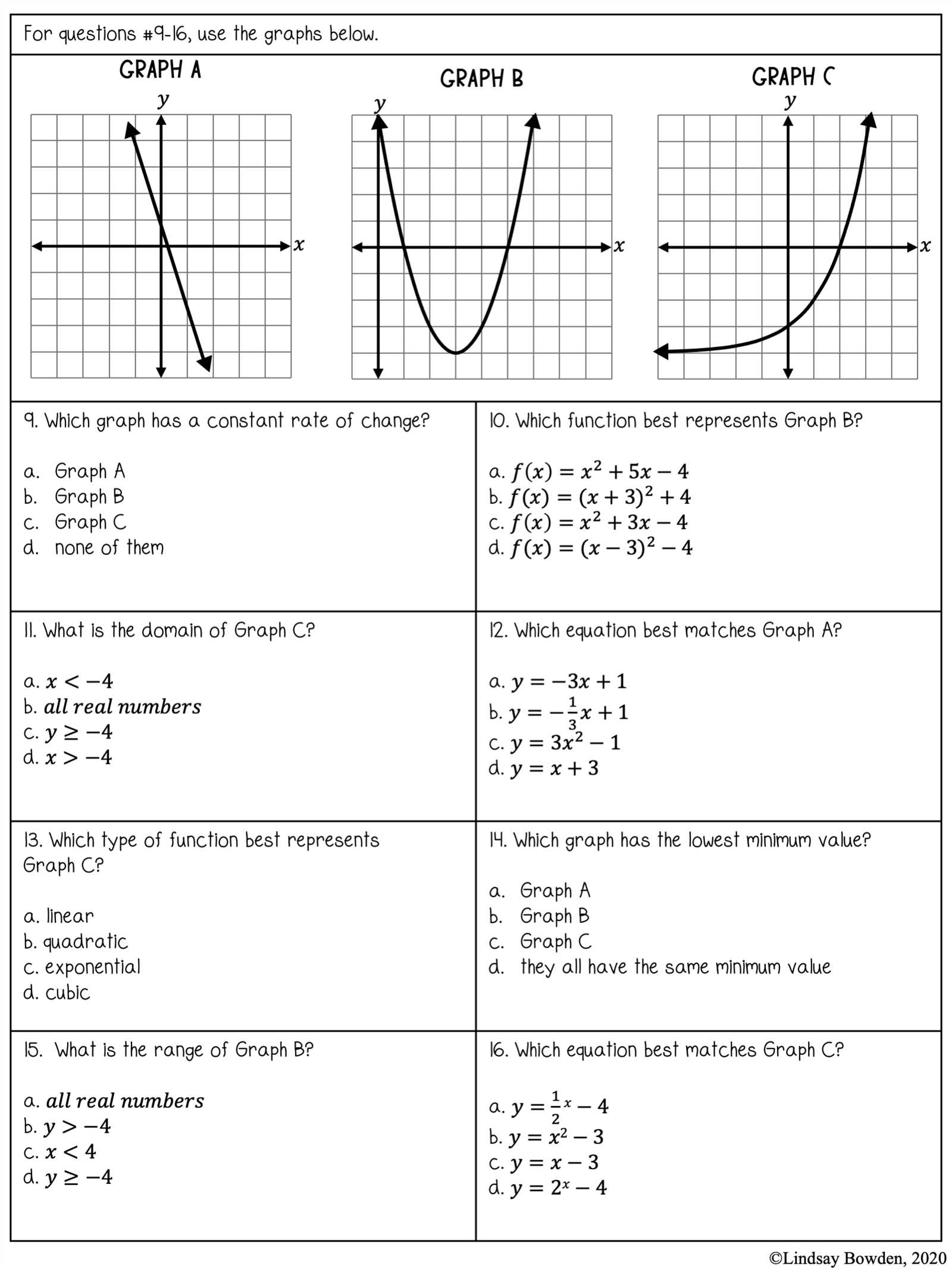
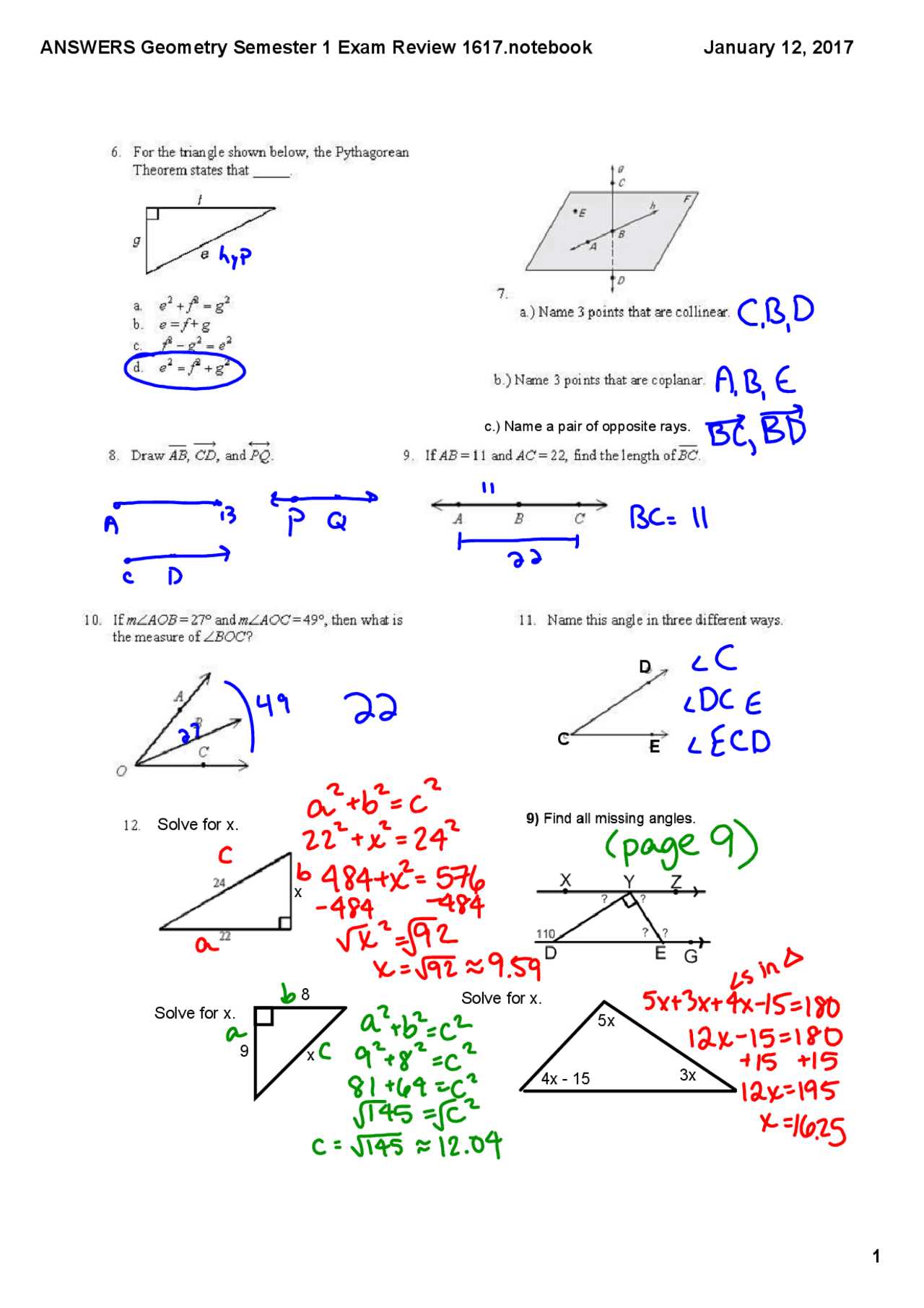
Geometry Final Exam Review Packet Answers

In this section, we will explore various mathematical concepts and problem-solving strategies essential for preparing for a comprehensive assessment. By understanding the underlying principles and applying them to different types of questions, you will be better equipped to navigate challenges efficiently and accurately. The following guide breaks down key areas that often appear in assessments, providing solutions and techniques to enhance your approach.

Key Topics to Focus On:

• Identifying and working with different shapes
• Understanding the relationships between angles and lines
• Applying algebraic methods to geometric problems
• Solving word problems involving spatial reasoning
• Working with coordinate-based problems

To help you prepare effectively, here are some common types of questions and strategies for solving them:

1. Shape Properties: Practice identifying different types of shapes, their properties, and how to calculate areas and volumes.
2. Angle Relationships: Learn the relationships between complementary, supplementary, and vertical angles, and how to solve for unknown values.
3. Proofs and Logical Reasoning: Mastering the step-by-step process of solving logical problems will help you approach proofs with confidence.
4. Coordinate Problems: Understand how to calculate distances, midpoints, and slopes using coordinate geometry principles.
5. Trigonometric Applications: Get familiar with trigonometric ratios and their applications to real-world problems.

By reviewing these areas and practicing sample problems, you will be better prepared to tackle any challenge. Understanding how to approach each question with a clear strategy will improve your ability to solve problems efficiently and correctly.

Key Concepts for Geometry Review

To excel in mathematical assessments, a solid grasp of fundamental principles is essential. Focus on understanding the core topics and building strong problem-solving techniques. The following concepts form the foundation for tackling various types of problems efficiently, ensuring you’re well-prepared to face any challenge.

Essential Topics to Master

• Shapes and Properties: Understanding the characteristics of different shapes and how to calculate their properties, such as area, perimeter, and volume, is crucial.
• Angles and Relationships: A strong understanding of angle properties, such as complementary, supplementary, and vertical angles, is fundamental for solving many problems.
• Symmetry and Transformations: Mastering concepts like reflections, rotations, and translations will help you recognize patterns and solve problems involving movement and symmetry.
• Coordinate Systems: Be familiar with calculating distances, midpoints, and slopes, as well as interpreting graphs and coordinates to solve spatial problems.

Problem-Solving Strategies

1. Work Step-by-Step: Break down complex problems into smaller, manageable parts. Solving each step methodically will help avoid mistakes.
2. Visualize the Problem: Drawing diagrams or graphs can make it easier to understand the relationships between different elements in a problem.
3. Use Formulas Wisely: Memorize key formulas and know when to apply them effectively for calculations involving areas, perimeters, angles, etc.
4. Practice Logical Reasoning: Focus on developing your reasoning skills by solving problems that require proofs or the application of mathematical logic.

By mastering these core principles and applying proven strategies, you’ll be well-equipped to solve problems confidently and accurately. Practice with a variety of questions to reinforce your skills and enhance your understanding of these key topics.

Essential Theorems to Know for the Exam

Understanding key mathematical principles and theorems is crucial for solving complex problems. These theorems provide the foundation for many types of questions, offering clear and concise rules for determining relationships between different elements. Mastering them will improve your ability to solve problems efficiently and accurately during assessments.

The following table outlines some of the most important theorems that will be helpful when tackling a wide range of problems:

Theorem	Statement	Application
Pythagorean Theorem	a² + b² = c²	Used to find the length of a side in a right triangle when two sides are known.
Triangle Sum Theorem	The sum of the angles in any triangle is always 180°.	Helps in solving for unknown angles in a triangle.
Vertical Angle Theorem	Vertical angles are congruent.	Useful for finding missing angle measurements when two lines intersect.
Parallel Line Theorem	If two parallel lines are cut by a transversal, alternate interior angles are congruent.	Helps in solving for angles when parallel lines are involved.
Angle Bisector Theorem	The angle bisector divides the opposite side into segments that are proportional to the adjacent sides.	Used to solve problems involving angle bisectors and proportions in triangles.

Familiarizing yourself with these theorems and practicing their application will help you approach problems with a strategic mindset, ensuring that you can solve questions with precision and clarity. Understanding when and how to apply each theorem is essential for success.

Step-by-Step Solutions for Geometry Problems

When approaching mathematical problems, breaking them down into smaller, manageable steps is essential. This process helps ensure accuracy and clarity, making it easier to arrive at the correct solution. By following a systematic approach, you can tackle even the most challenging questions with confidence.

Solving Problems Involving Shapes and Angles

To solve problems involving various shapes and angles, follow these steps:

• Identify Known Values: Carefully examine the given information and identify the values you know (e.g., side lengths, angle measures).
• Choose the Right Formula: Select the appropriate formula based on the type of problem you’re solving, whether it’s calculating area, perimeter, or angles.
• Set Up the Equation: Use the identified values and substitute them into the chosen formula to set up your equation.
• Solve the Equation: Perform the necessary algebraic steps to solve for the unknown value, ensuring each step is executed correctly.
• Check Your Work: After reaching an answer, double-check the calculations to ensure the solution makes sense in the context of the problem.

Working with Coordinate Geometry

Coordinate-based problems often involve finding distances, midpoints, or slopes. Here’s how to solve them:

• Plot the Points: If not already given, plot the points on a coordinate plane to visualize the problem.
• Apply the Distance Formula: To find the distance between two points, use the formula √((x₂ – x₁)² + (y₂ – y₁)²).
• Calculate the Midpoint: To find the midpoint between two points, use the formula ((x₁ + x₂)/2, (y₁ + y₂)/2).
• Determine the Slope: To calculate the slope between two points, use (y₂ – y₁) / (x₂ – x₁).

By following these structured steps, you can systematically work through problems, ensuring that each part of the solution is addressed and that the final answer is both accurate and logical.

Understanding Geometric Proofs and Applications

Mathematical proofs are essential tools for demonstrating the validity of certain properties or relationships within various figures. Through logical reasoning, these proofs establish facts that can be applied to solve complex problems. A strong understanding of how to approach proofs, as well as how to apply the results to real-world scenarios, is key to mastering these types of challenges.

Key Steps in Constructing a Proof

When constructing a proof, it’s important to follow a clear sequence of logical steps to arrive at a valid conclusion. Here’s a general approach:

• State the Given Information: Begin by listing all the information provided in the problem. This includes measurements, relationships, and any known properties.
• Establish What Needs to be Proven: Clearly define what you are attempting to prove. This could be an equality, a property, or a relationship between different elements.
• Apply Known Theorems and Properties: Use relevant mathematical principles and theorems that support your reasoning. This might include angle relationships, congruence properties, or proportionality.
• Work Step-by-Step: Break down the proof into logical steps, ensuring each one follows from the previous step. Avoid jumping to conclusions and make sure your reasoning is sound.
• Conclude the Proof: Once all the steps have been completed and the required result is achieved, formally conclude that the proof is complete.

Real-World Applications of Proofs

The beauty of geometric proofs lies not only in their logical structure but also in their practical applications. Understanding how to apply proven properties can help solve real-world problems, such as:

• Design and Architecture: Proofs are used in construction and design to ensure the stability and functionality of structures, especially when calculating angles and distances.
• Engineering: Geometric principles are fundamental in designing mechanical systems, ensuring precision in parts and movements.
• Navigation and Mapping: Using proven principles, navigators and cartographers can accurately map out distances, routes, and locations.
• Computer Graphics: Proofs help in rendering precise shapes and objects on screens, particularly in 3D modeling and animation.

By mastering the process of constructing proofs and understanding how to apply their results, you can approach complex problems with confidence and precision, making these skills valuable in both academic and real-world contexts.

Common Geometry Mistakes to Avoid

When working through mathematical problems, it’s easy to make mistakes that can lead to incorrect solutions. Recognizing common errors and knowing how to avoid them is crucial for ensuring accuracy and improving problem-solving skills. Understanding these pitfalls will help you approach each question more carefully and confidently.

Overlooking Key Information

One of the most common mistakes is failing to use all the given information. Carefully read through each problem to ensure you don’t miss any important details, such as measurements, angles, or relationships between elements. Missing even one key piece of data can result in incorrect calculations and conclusions.

• Double-check: Always go back and review the provided information before starting to solve the problem.
• Look for hidden relationships: Sometimes, the problem includes information that can be used indirectly, such as symmetry or congruence that may not be immediately obvious.

Misapplying Formulas

Another common error is using the wrong formula or applying a formula incorrectly. It’s essential to choose the correct method for the type of problem you’re solving, whether it involves areas, perimeters, volumes, or angles.

• Know the formulas: Memorize key formulas and understand how they are derived so you can apply them accurately.
• Watch for specific conditions: Be mindful of any special conditions that may require a variation of the standard formula, such as using a different approach for non-right triangles or circles.

Skipping Logical Steps

Many problems require a logical progression of steps to reach the correct solution. Skipping or rushing through steps can lead to errors, especially when dealing with complex calculations or proofs.

• Work step-by-step: Always break down complex problems into smaller, manageable steps to avoid overlooking important details.
• Check each step: After completing each step, verify that the reasoning and calculations are correct before moving on.

By avoiding these common mistakes and adopting a careful, systematic approach, you’ll improve your ability to solve problems accurately and effectively. Practice and attention to detail are key to mastering the subject and avoiding these pitfalls.

Strategies for Solving Geometry Word Problems

Word problems can often seem daunting, but with the right approach, they can be broken down into manageable steps. The key is to translate the narrative into mathematical terms and apply relevant concepts and formulas. By following a structured strategy, you can simplify complex problems and increase your chances of finding the correct solution.

Understand the Problem

The first step in solving any word problem is to fully understand what is being asked. Read the problem carefully, and identify the key information and the goal of the question.

• Highlight important details: Mark the given values, relationships, and any specific conditions mentioned in the problem.
• Identify what needs to be found: Pay attention to the specific quantity you need to calculate, whether it’s a distance, area, or angle.

Draw a Diagram

Visualizing the problem is one of the most effective strategies for solving word problems. A diagram can help you see relationships between elements and assist in identifying the correct formula to apply.

• Label all known values: Clearly mark any given measurements on the diagram to ensure you use them in your calculations.
• Include all relevant shapes and angles: Draw all the figures mentioned in the problem and label them with the necessary information.

Translate Words into Equations

Once you have understood the problem and drawn the diagram, the next step is to convert the words into mathematical equations. This is where you apply the relevant formulas and relationships to form the solution process.

• Use known formulas: Based on the problem type, choose the appropriate formulas for area, perimeter, volume, or angle relationships.
• Set up an equation: Translate the word problem into an equation using the identified values and the formulas you’ve selected.

Perform Calculations and Solve

Now that you have the equation, you can proceed with solving the problem. Be careful to perform each step systematically to avoid errors.

• Check each step: Make sure every part of the equation is simplified correctly, and no calculations are skipped.
• Double-check your work: After arriving at a solution, go over the calculations again to ensure everything is accurate.

Review the Solution

Once you’ve found a solution, it’s important to review the answer in the context of the original problem. Does the solution make sense based on the given information? Are the units correct? Review to make sure everything aligns with the problem statement.

• Check for reasonableness: Ensure that the solution is logical and fits within the context of the problem.
• Verify units: Ensure that the units in your solution match the units in the problem (e.g., meters, degrees).

By following these steps, you can approach word problems with confidence and systematically work through them to find the correct solution. Practice is essential, so keep applying these strategies to improve your problem-solving skills.

Reviewing Geometric Shapes and Properties

Understanding the characteristics of various shapes and their properties is fundamental to solving mathematical problems. Each figure has its own set of attributes, such as angles, sides, and symmetries, which can be used to solve problems and prove relationships. Familiarity with these properties enables a deeper understanding and more efficient problem-solving approach.

Key Properties of Common Shapes

Every shape has a unique set of properties that define its structure. Recognizing these properties can help in identifying which formulas and theorems to apply when solving problems.

• Triangles: A triangle has three sides and three angles. The sum of the angles in any triangle is always 180 degrees. Special triangles, such as equilateral, isosceles, and scalene, have their own specific properties.
• Quadrilaterals: Quadrilaterals are four-sided figures. Common examples include squares, rectangles, parallelograms, and trapezoids. Each has specific properties regarding sides, angles, and symmetry.
• Circles: A circle is defined by its radius, diameter, and circumference. Important properties include the relationship between the radius and the circumference (C = 2πr) and the area (A = πr²).
• Polygons: Polygons are multi-sided shapes. The sum of the interior angles of a polygon is determined by the formula (n-2) × 180°, where n is the number of sides.

Symmetry and Congruence

Symmetry plays a key role in understanding the properties of shapes. A shape is symmetrical if it can be divided into two identical parts. Congruence refers to two figures having the same shape and size, and can be applied to solve many types of problems.

• Symmetry: Shapes can have line symmetry (mirror symmetry) or rotational symmetry. Recognizing these symmetries can simplify calculations, such as when dividing figures into equal parts.
• Congruent Figures: When two figures are congruent, their corresponding sides and angles are equal. This property is important for solving problems involving equal lengths and angles.

By becoming familiar with the properties of various shapes and their symmetries, you’ll be better equipped to tackle complex problems and prove important mathematical concepts with confidence.

Angles and Their Properties in Geometry

Angles are fundamental components in the study of shapes and space, influencing a wide range of geometric relationships. They describe the rotation between two intersecting lines or segments and are essential in understanding the structure of figures. Mastering angle properties is crucial for solving problems involving polygons, triangles, and other geometric constructs.

Angles are classified by their measures, and their relationships are vital for reasoning about other properties, such as parallelism, symmetry, and congruence. Below are the main types of angles and their corresponding properties.

Types of Angles

Understanding the different types of angles is the first step in mastering their properties. Here is a table that outlines the key types of angles:

Angle Type	Description	Measure Range
Acute Angle	An angle that is less than 90 degrees.	0°
Right Angle	An angle that is exactly 90 degrees.	90°
Obtuse Angle	An angle that is greater than 90 degrees but less than 180 degrees.	90°
Straight Angle	An angle that is exactly 180 degrees.	180°
Reflex Angle	An angle greater than 180 degrees but less than 360 degrees.	180°

Angle Relationships

Angles interact with each other in various ways, creating important relationships that are used in problem-solving. Recognizing these relationships can significantly simplify calculations and reasoning.

• Complementary Angles: Two angles are complementary if their measures add up to 90 degrees.
• Supplementary Angles: Two angles are supplementary if their measures add up to 180 degrees.
• Adjacent Angles: Two angles are adjacent if they share a common side and vertex, but do not overlap.
• Vertical Angles: When two lines intersect, the opposite angles formed are called vertical angles, and they are always equal.

By understanding these fundamental properties, you can work with angles confidently and apply this knowledge to a variety of problems, from calculating unknown angle measures to proving geometric theorems.

How to Approach Coordinate Geometry Questions

Understanding how to work with points, lines, and shapes on a coordinate plane is essential for solving spatial problems. These types of questions typically involve applying formulas and understanding the relationships between coordinates to solve for unknown values. Developing a clear, systematic approach can help in tackling problems efficiently and accurately.

When approaching questions that involve coordinates, the first step is to identify what is being asked. Whether it’s finding the distance between two points, determining the slope of a line, or calculating the area of a shape, recognizing the specific task will guide you toward the right approach. Here are some key techniques to keep in mind:

• Use the Distance Formula: The distance between two points (x₁, y₁) and (x₂, y₂) on a plane is calculated using the formula: d = √((x₂ – x₁)² + (y₂ – y₁)²).
• Apply the Slope Formula: To find the slope of a line passing through two points, use the formula: m = (y₂ – y₁) / (x₂ – x₁). This is useful for determining the direction of the line.
• Equation of a Line: Once you have the slope, you can find the equation of the line using the point-slope form: y – y₁ = m(x – x₁). This is helpful for describing lines in coordinate space.
• Identifying Shapes: Use the properties of shapes and their coordinate-based formulas. For example, a rectangle’s area can be found by multiplying the length and width, which can be derived from the distance formula.

By breaking down the problem into smaller parts and applying these formulas and principles, you can approach coordinate-based problems in a more organized and effective manner, ensuring you don’t miss any critical steps.

Mastering Transformations in Geometry

Transformations play a critical role in understanding how shapes can be manipulated and mapped from one position to another within a coordinate system. Mastering these transformations not only enhances your problem-solving skills but also helps in visualizing geometric concepts and their relationships. There are several types of transformations, each with its unique properties and applications.

Understanding the basic types of transformations will give you the tools needed to tackle more complex problems. The four main transformations are translation, rotation, reflection, and dilation. Here’s an overview of these transformations and their key features:

Types of Transformations

• Translation: This involves shifting a figure from one position to another without altering its size, shape, or orientation. It’s essentially a “sliding” of the figure along a straight path. The translation is defined by the horizontal and vertical movement along the x and y axes.
• Rotation: Rotation involves turning a figure around a fixed point, known as the center of rotation. The angle of rotation and the direction (clockwise or counterclockwise) determine the new position of the figure. Understanding the degrees of rotation (90°, 180°, 270°) is essential when working with this transformation.
• Reflection: A reflection flips a figure over a line (called the line of reflection), creating a mirror image. The position of the points is inverted in relation to the line, but the shape and size remain unchanged. This transformation is often used to explore symmetry in geometric figures.
• Dilation: Dilation changes the size of a figure by expanding or contracting it while maintaining its shape. The center of dilation remains fixed, and the figure’s dimensions are scaled by a certain factor. This transformation is useful in studying similarity and proportionality.

Key Concepts to Understand

• Mapping Notation: Each transformation can be described using coordinates. For instance, a translation is represented by adding specific values to the coordinates of a figure’s vertices, while a rotation or reflection may involve a more complex relationship depending on the angle or line of reflection.
• Congruence and Similarity: Transformations help establish the concepts of congruence (when figures are identical in shape and size) and similarity (when figures have the same shape but different sizes). Dilations are particularly important when studying similarity, as they involve scaling figures proportionally.
• Combining Transformations: Often, multiple transformations are combined to solve problems. For example, a figure might first be rotated, then reflected, or dilated after a translation. Understanding how to combine transformations effectively is key to solving more advanced geometric problems.

By mastering these transformations and their properties, you can better understand how geometric objects interact and how their positions and sizes change within a coordinate system. This knowledge is essential for solving complex problems that require a solid grasp of shape manipulation and spatial reasoning.

Solving Trigonometry Problems in Geometry

Trigonometry provides the essential tools for solving problems involving angles and lengths in triangles and other shapes. By applying trigonometric ratios and functions, you can determine unknown measurements, analyze spatial relationships, and solve complex problems in various contexts. A strong understanding of these principles is crucial for successfully tackling questions that involve right triangles and other geometric shapes.

To approach trigonometric problems effectively, it’s important to remember the primary trigonometric ratios: sine, cosine, and tangent. These ratios relate the angles of a triangle to the lengths of its sides and can be used to find unknown lengths or angles in a given problem. Here’s a breakdown of how these ratios are applied:

Basic Trigonometric Ratios

• Sine (sin): This ratio compares the length of the side opposite an angle to the hypotenuse of the triangle. It is represented as: sin(θ) = opposite / hypotenuse.
• Cosine (cos): This ratio compares the length of the adjacent side to the hypotenuse. It is represented as: cos(θ) = adjacent / hypotenuse.
• Tangent (tan): This ratio compares the length of the opposite side to the adjacent side. It is represented as: tan(θ) = opposite / adjacent.

Using Trigonometric Ratios in Problem Solving

• Finding an unknown side: If you know one angle and one side of a right triangle, you can use the appropriate trigonometric ratio to solve for an unknown side. For example, if you know the angle and the hypotenuse, use sine or cosine to find the missing side.
• Finding an unknown angle: If you know the sides of a right triangle, you can use inverse trigonometric functions (such as sin⁻¹, cos⁻¹, or tan⁻¹) to find the measure of an unknown angle.
• Solving word problems: Trigonometry is often used in word problems where you need to apply the trigonometric ratios to real-world situations, such as determining the height of a building, the distance across a river, or the angle of elevation or depression.

By applying these techniques and understanding the relationships between angles and sides in right triangles, you can solve a wide range of trigonometric problems efficiently. The key is to practice recognizing when and how to apply the appropriate trigonometric ratios to find unknown values and work through problems systematically.

Geometry Word Problem Practice with Solutions

Word problems are an essential part of understanding spatial relationships and applying mathematical principles to real-world scenarios. These problems often require you to translate verbal descriptions into mathematical equations or figures and then solve for unknown quantities. By practicing with a variety of problems, you can strengthen your problem-solving skills and improve your ability to apply geometric concepts to practical situations.

In this section, we will explore several common types of problems, providing clear step-by-step solutions to help you understand the approach for each one. This practice will enhance your ability to analyze and solve complex situations effectively.

Problem 1: Finding the Height of a Triangle

A right triangle has a base of 12 cm and a hypotenuse of 13 cm. What is the height of the triangle?

Solution:

• We can use the Pythagorean theorem: a² + b² = c², where c is the hypotenuse and a and b are the legs of the triangle.
• Let the height of the triangle be b. We know that c = 13 cm and a = 12 cm.
• Substitute the known values into the equation: 12² + b² = 13².
• 144 + b² = 169
• Subtract 144 from both sides: b² = 25.
• Take the square root of both sides: b = 5 cm.

The height of the triangle is 5 cm.

Problem 2: Area of a Circle

What is the area of a circle with a radius of 7 cm?

Solution:

• The formula for the area of a circle is A = πr², where r is the radius.
• Substitute r = 7 cm into the formula: A = π(7)² = π(49).
• Using π ≈ 3.14, the area is approximately: A ≈ 3.14 × 49 = 153.86 cm².

The area of the circle is approximately 153.86 cm².

Problem 3: Perimeter of a Rectangle

A rectangle has a length of 8 cm and a width of 5 cm. What is the perimeter of the rectangle?

Solution:

• The formula for the perimeter of a rectangle is P = 2l + 2w, where l is the length and w is the width.
• Substitute the given values: P = 2(8) + 2(5).
• P = 16 + 10 = 26 cm.

The perimeter of the rectangle is 26 cm.

By practicing problems like these and following a structured approach, you can develop a stronger understanding of how to apply geometric principles to real-world situations. Whether you’re calculating areas, solving for missing lengths, or analyzing angles, these practice problems will help sharpen your skills and increase your confidence in tackling complex challenges.

Important Formulas for Geometry Exams

Mastering key formulas is essential for solving mathematical problems efficiently. These formulas provide the foundation for finding areas, volumes, angles, and other critical measurements in various shapes and figures. Understanding and memorizing them is crucial for applying the right techniques to any problem you encounter.

In this section, we will highlight the most important formulas you should know, focusing on shapes and their properties. These will serve as a valuable reference for solving problems quickly and accurately.

Area and Perimeter Formulas

• Rectangle:
  • Area: A = l × w (where l is length and w is width)
  • Perimeter: P = 2l + 2w
• Triangle:
  • Area: A = 1/2 × b × h (where b is base and h is height)
  • Perimeter: P = a + b + c (where a, b, c are the sides)
• Circle:
  • Area: A = πr² (where r is the radius)
  • Circumference: C = 2πr

Volume and Surface Area Formulas

• Cube:
  • Volume: V = s³ (where s is the side length)
  • Surface Area: SA = 6s²
• Sphere:
  • Volume: V = 4/3πr³
  • Surface Area: SA = 4πr²
• Cylinder:
  • Volume: V = πr²h (where h is the height)
  • Surface Area: SA = 2πrh + 2πr²

These formulas are indispensable tools when solving problems related to spatial reasoning and measurements. By memorizing and understanding them, you’ll be able to efficiently calculate areas, perimeters, volumes, and surface areas for various shapes, which will be key to excelling in solving related problems.

Visualizing Geometry Problems for Better Understanding

Understanding complex problems becomes significantly easier when you can visualize the figures and their relationships. By drawing diagrams, labeling key points, and identifying geometric properties, you can break down a problem into simpler, more manageable parts. This approach is especially helpful when dealing with spatial reasoning and abstract concepts that may seem challenging at first glance.

Visualization allows you to see how different elements interact within a figure, such as angles, sides, and shapes. It helps you to recognize patterns and identify the correct methods for solving a problem. Below are some strategies that can enhance your ability to approach problems effectively by visualizing them.

• Draw the Figure: Always start by sketching the given problem. Even if a figure is provided, redraw it to scale or to your understanding. This ensures you’re accurately interpreting the problem’s details.
• Label Key Information: Label important points, lengths, angles, and other relevant data within your diagram. Clear labeling allows you to track and use the necessary values for solving the problem.
• Break Down Complex Shapes: When faced with a compound shape, break it down into simpler shapes (such as rectangles, triangles, and circles). Solve for individual areas or properties and combine the results.
• Identify Symmetry: Many geometric figures exhibit symmetry. Recognizing symmetrical properties can help reduce the complexity of a problem, as it allows you to focus on only a portion of the figure.
• Use Color Coding: Use different colors to highlight various parts of the figure. This can make it easier to differentiate between similar parts of a complex figure and avoid confusion.

With practice, visualizing these problems will become second nature. The ability to effectively map out and analyze a problem’s structure leads to more accurate and faster solutions. Embrace this technique as a powerful tool in mastering spatial problems and concepts.

Tips for Efficient Geometry Exam Time Management

Time management is a crucial skill when tackling any assessment. By using your allotted time wisely, you can avoid unnecessary stress and ensure that every question gets the attention it needs. Effective time management during assessments involves not only solving problems quickly but also allocating time to review and adjust your approach as needed. Below are strategies that can help you make the most of your time while tackling problems.

Strategies for Managing Your Time

• Prioritize Questions: Start by quickly scanning the test and identifying questions you are most confident in. Answer these first to gain momentum and boost your confidence. Save more difficult questions for later.
• Allocate Time for Each Section: Set specific time limits for each section or type of problem. This helps ensure that you don’t spend too long on any one question, giving yourself a chance to address every part of the test.
• Use Scratch Paper Efficiently: For complex problems, use scratch paper to jot down notes, diagrams, or formulas. This helps you visualize the problem more clearly and reduces the time spent reworking difficult questions.
• Don’t Get Stuck: If you find yourself stuck on a question, move on. It’s better to spend time on questions you can solve, and return to more difficult ones later with a fresh perspective.
• Review and Check: If time permits, always leave a few minutes at the end to review your answers. Check for any mistakes, overlooked details, or missed steps to ensure the accuracy of your work.

Time Management Chart

Section	Time Allocation	Strategy
Quick Questions	20%	Complete first to build confidence
Moderate Difficulty	50%	Allocate the most time to these questions
Challenging Problems	20%	Attempt last, if time permits
Review	10%	Check for mistakes or incomplete answers

By implementing these time management techniques, you can approach your next assessment with a calm and organized mindset, allowing you to perform at your best.