Glencoe Geometry Final Exam Answers Guide

Preparing for an important academic challenge requires a clear understanding of the material and the ability to apply learned principles effectively. Whether you’re tackling abstract problems or solving practical scenarios, honing your skills is essential for success. This section is designed to guide you through the crucial steps and provide support as you work towards mastering complex topics.

Focusing on core topics will ensure that you are well-equipped to handle a variety of questions that may arise. Emphasizing both theoretical understanding and hands-on practice will build your confidence and ability to think critically under pressure. It’s not just about knowing the material but about applying it in ways that make sense.

By developing a clear strategy for your preparation, you’ll be able to navigate through the material efficiently. Knowing how to break down problems, review key concepts, and avoid common pitfalls will give you a significant advantage. This approach will also help you manage your time effectively, ensuring you stay on track while tackling challenges.

Mathematics Assessment Solutions

Successfully navigating through a complex assessment involves more than just memorization; it requires a deep understanding of the core principles and the ability to apply them in various situations. This section aims to provide insights into the critical techniques and thought processes needed to excel in your academic challenge. With the right approach, you can confidently tackle any problem that comes your way.

Building a Strong Foundation

To perform well, it’s essential to first build a strong foundation in the key concepts. Understanding how to manipulate equations, interpret geometric figures, and apply logical reasoning will significantly impact your performance. By focusing on these foundational skills, you can approach more complex problems with clarity and confidence.

Effective Problem-Solving Strategies

Developing a structured method for solving problems can drastically improve your efficiency. Break down each question into manageable steps, identify the relevant information, and apply the appropriate techniques. This will help you stay organized, reduce errors, and ensure that your solutions are both accurate and well-structured.

Comprehensive Review of Key Concepts

A solid understanding of fundamental ideas is crucial for success in any academic challenge. By reviewing core principles, you can strengthen your grasp on essential topics and improve your ability to solve complex problems. This section focuses on revisiting the most important concepts that will help you approach various tasks with confidence and clarity.

Revisiting foundational ideas will allow you to recognize patterns and relationships that often appear in assessments. These core elements provide the building blocks for more advanced techniques, ensuring that you can apply them with ease. Whether you’re solving equations or working through logical steps, a clear grasp of the basics will enable you to proceed with confidence.

It’s also important to recognize the connections between different concepts. Many problems require the integration of multiple principles, and understanding how they relate to one another will provide a clearer path to the solution. The more familiar you are with these interconnections, the easier it will be to navigate through challenging tasks.

Understanding the Assessment Format

Familiarity with the structure of an academic assessment is key to performing well. Knowing what to expect in terms of question types, difficulty level, and the overall layout can help you prepare more effectively. This section will break down the typical structure, so you can approach each section with a clear strategy and confidence.

The format usually consists of a variety of question types, each designed to test different skills. Some questions may require straightforward calculations, while others will challenge your reasoning abilities or test your knowledge of key principles. Being aware of these variations allows you to adjust your approach accordingly.

Question Type	Description	Typical Focus
Multiple Choice	Choose the correct option from several choices.	Recall of formulas and basic principles
Short Answer	Provide a direct solution to the given problem.	Application of concepts in real scenarios
Long Answer	Write a detailed explanation and solve the problem step by step.	Critical thinking and problem-solving
Diagram-based	Interpret and work with graphical representations.	Spatial understanding and visualization

Understanding these categories will help you allocate time and effort based on the type of task at hand. With this knowledge, you can tailor your study sessions to cover each area effectively, ensuring you’re well-prepared when it’s time to tackle the real challenge.

Step-by-Step Problem Solving Techniques

Approaching complex challenges in a methodical way can make problem-solving more manageable and efficient. By breaking down a task into smaller, logical steps, you can tackle even the most difficult problems with confidence. This section will explore key strategies to guide you through the process and ensure you reach the correct solution every time.

One of the most effective ways to solve a problem is to follow a structured approach. This involves clearly defining the problem, identifying the necessary steps, and applying relevant principles. Below is a suggested framework to help you work through problems more efficiently:

Understand the Problem: Carefully read the question to ensure you understand what is being asked. Pay attention to keywords and details.
Identify Known Information: Write down the given values or information. This will serve as a foundation for your solution.
Choose a Strategy: Decide on the appropriate method or formula to use based on the problem type. This could include drawing diagrams, using equations, or applying logical reasoning.
Execute the Plan: Apply your chosen strategy step by step. Be sure to follow each part of the process carefully to avoid mistakes.
Check Your Work: After arriving at a solution, review your steps to ensure accuracy. Verify that the result makes sense in the context of the question.

By using this approach, you’ll be able to systematically solve problems while minimizing errors. Practicing this technique regularly will not only enhance your skills but also boost your confidence when facing a wide variety of challenges.

Common Mistakes in Mathematics Assessments

Even the most well-prepared individuals can make errors during a challenging assessment. These mistakes often arise from simple oversights or a lack of attention to detail. Recognizing these common pitfalls is essential to avoiding them and improving your performance. This section highlights typical errors that students make, along with strategies to prevent them.

Many of these mistakes stem from misunderstanding the question or misapplying techniques. Below are some of the most frequently encountered errors:

Misreading the Problem: Failing to carefully read the question can lead to incorrect interpretations. Always ensure you fully understand the requirements before starting to solve.
Skipping Units: Forgetting to include or convert units can lead to incorrect answers. Double-check that all measurements are properly accounted for.
Incorrect Formula Usage: Using the wrong formula or applying it incorrectly is a common issue. Always confirm that you’re using the appropriate method for the problem.
Rushing Through Steps: Skipping intermediate steps or failing to show your work can result in mistakes that are difficult to catch. Take the time to work through each step carefully.
Overlooking Diagrams: Ignoring or misinterpreting diagrams can lead to errors in spatial reasoning. Ensure that you carefully analyze any provided illustrations.
Calculation Errors: Simple arithmetic mistakes can drastically affect the outcome. Verify your calculations, especially in multi-step problems.

By being aware of these common errors, you can take steps to avoid them in your own work. Practice, attention to detail, and careful review are the keys to minimizing mistakes and achieving better results.

Tips for Efficient Time Management During Assessments

Managing your time effectively during a challenging assessment is crucial to ensuring that you can complete all tasks within the given time limit. Without proper time management, even the most prepared students can struggle to finish on time or make careless mistakes. This section provides practical tips on how to allocate your time wisely and stay organized throughout the test.

Prioritize the questions based on difficulty. Start with the ones you feel most confident about to secure quick points, then move on to the more challenging tasks. This approach will help build momentum and prevent wasting time on difficult questions early on.

It’s also helpful to set specific time limits for each section of the test. By giving yourself a set amount of time for each question or group of questions, you’ll prevent yourself from spending too long on any single part. Use a watch or clock to keep track of time, and be mindful of the remaining minutes.

Start with a quick scan: Review the entire test to get a sense of the question types and difficulty. This will help you plan your strategy.
Allocate time wisely: Divide your time according to the weight of each section or question. More complex problems may require additional time.
Keep track of time: Check the clock periodically to ensure you’re staying on schedule. Avoid spending too much time on any single question.
Move on if stuck: If you find yourself struggling with a question, mark it and move on. Return to it later with fresh eyes if time allows.
Leave time for review: Ensure you have a few minutes at the end to go over your answers, check calculations, and correct any mistakes.

By using these time management strategies, you can optimize your performance and ensure that you give every question the attention it deserves without feeling rushed. Consistent practice of these techniques will help you improve your efficiency over time.

Breaking Down Complex Problems

When faced with a difficult task, breaking it down into smaller, manageable parts is the most effective strategy. Complex problems often involve multiple steps or concepts, and trying to solve them all at once can be overwhelming. By dissecting the problem into its core components, you can approach each part systematically and find the solution more easily.

Start by identifying the key elements of the problem. What are the known values, and what needs to be determined? Next, organize the information by drawing diagrams or writing down formulas that are relevant. This helps clarify the situation and gives you a visual representation to work with.

Once you’ve broken the problem down, apply logical steps one by one. Focus on solving smaller parts of the problem before putting everything together. This method prevents you from feeling overwhelmed and increases the likelihood of finding a correct solution. Finally, double-check your work to ensure that each step is accurate before proceeding to the next one.

Understanding the Theorems

Mastering theorems is essential for solving complex problems efficiently. These fundamental principles act as the building blocks for understanding and proving relationships between different elements. A strong grasp of key theorems allows you to solve a variety of tasks systematically and confidently, providing a solid foundation for more advanced problem-solving techniques.

Theorems often represent established truths that can be applied across different scenarios, so knowing when and how to use them is crucial. Understanding their proofs and how they are derived gives you deeper insights into why certain relationships hold true and how to apply them effectively.

Key Theorems to Know

Familiarity with these essential theorems is key to successfully applying them in various contexts:

Pythagorean Theorem: A foundational principle used to determine the relationship between the sides of a right triangle.
Angle Sum Theorem: States that the sum of angles in any triangle is always 180 degrees.
Parallel Line Theorem: Describes the relationship between angles formed by parallel lines and a transversal.

Application in Problem-Solving

When tackling problems, it’s important to recognize the appropriate theorems that can simplify your approach. Whether you’re solving for unknown angles, proving congruence, or working with shapes and their properties, applying these principles in the right context can greatly reduce complexity and improve accuracy.

How to Use Practice Tests Effectively

Practice tests are one of the most valuable tools for preparing for any challenging assessment. They simulate the real test environment, helping you become familiar with the format and types of questions you may encounter. More importantly, they allow you to identify areas of strength and weakness, so you can focus your efforts where they’re most needed. By using practice tests strategically, you can maximize your preparation and improve your performance.

It’s essential to approach practice tests with purpose. Simply taking the tests without reviewing your results won’t yield the best outcomes. Instead, aim to learn from each test, understanding not just the correct answers, but also the reasoning behind them.

Effective Practice Test Strategies

Simulate Test Conditions: Take practice tests under timed conditions to mimic the actual assessment environment. This helps you build stamina and manage time effectively during the real test.
Review Mistakes Thoroughly: After completing a practice test, spend time reviewing every mistake. Understand why the correct answer is what it is and what you did wrong to ensure you don’t make the same error again.
Focus on Weak Areas: Identify the topics or question types that challenge you the most. Use practice tests to target these areas, ensuring you understand the underlying concepts before taking the real test.

Tracking Your Progress

As you complete multiple practice tests, track your scores and note any recurring mistakes. Monitoring your progress will give you valuable insights into how well you’re mastering the material. It also helps boost your confidence as you see improvement over time.

Common Question Types in Assessments

Understanding the common question formats you may encounter during an assessment is crucial for effective preparation. These types of questions are designed to test different aspects of your knowledge, from basic principles to more complex reasoning. By recognizing the most frequently asked question types, you can focus your study efforts on mastering each area and improve your chances of success.

Typical Question Formats

Multiple Choice Questions: These questions provide several possible answers, and you must select the correct one. They test both your understanding and ability to recognize the right solution from a set of choices.
True or False Questions: Simple statements where you must determine whether they are correct or incorrect. These questions assess your basic knowledge of core concepts.
Short Answer Questions: These require you to provide a brief explanation or solution, often involving calculations or the application of specific principles.
Proof-Based Questions: These questions ask you to prove a certain relationship or property using logical reasoning, often involving a sequence of steps based on established principles.

Problem-Solving and Application

Word Problems: These scenarios require you to extract relevant information from a description and apply appropriate methods to find the solution. They often combine multiple concepts and test your ability to think critically.
Diagrams and Visuals: Questions may include diagrams of shapes, angles, or figures where you need to apply your knowledge to identify relationships or solve for unknowns based on visual cues.

Familiarity with these question types will allow you to practice effectively and build confidence. By understanding how different question formats assess your knowledge, you can refine your approach and ensure you are well-prepared for the assessment ahead.

Formulae to Remember

Having a strong grasp of essential formulas is key to solving problems efficiently. These formulas serve as the foundation for various problem-solving techniques, allowing you to apply specific rules to determine unknown values and prove relationships between different elements. Memorizing these formulas not only saves time but also strengthens your understanding of fundamental principles.

Essential Area and Perimeter Formulas

Area of a Rectangle: Area = length × width
Area of a Triangle: Area = 1/2 × base × height
Perimeter of a Rectangle: Perimeter = 2 × (length + width)
Perimeter of a Triangle: Perimeter = sum of all sides
Area of a Circle: Area = π × radius²
Circumference of a Circle: Circumference = 2 × π × radius

Key Volume and Surface Area Formulas

Volume of a Cube: Volume = side³
Volume of a Rectangular Prism: Volume = length × width × height
Surface Area of a Cube: Surface Area = 6 × side²
Surface Area of a Cylinder: Surface Area = 2π × radius × (height + radius)

Remembering these formulas will help you tackle a wide range of problems and complete tasks more efficiently. Regularly reviewing and applying them will ensure that you have the necessary tools to approach complex problems with confidence.

Mastering Proofs and Reasoning

Developing a solid understanding of logical reasoning and proofs is essential for solving many problems. These skills enable you to demonstrate the validity of statements and relationships through a series of logical steps. By mastering the structure of proofs, you can confidently tackle complex tasks, showing the relationships between various concepts and providing clear justifications for your conclusions.

Proofs require a methodical approach, where each statement or step is supported by a valid reason, often based on previously established principles. This logical structure ensures that the conclusions drawn are sound and reliable. There are several key strategies to keep in mind when working through proofs:

Understand the Theorems: Knowing the fundamental principles and theorems is crucial, as they provide the basis for many proofs.
Break Down the Problem: Approach the problem step by step, isolating what you know and what needs to be proven.
Use Direct and Indirect Reasoning: Direct proofs involve straightforward steps, while indirect reasoning may involve proof by contradiction or contrapositive.
Work Backwards: Sometimes it’s helpful to work backwards from the desired conclusion to identify the steps leading up to it.

By consistently practicing proofs and reasoning techniques, you can improve your problem-solving abilities and strengthen your overall understanding of mathematical relationships. The more you practice, the more intuitive these methods become, allowing you to tackle increasingly difficult problems with ease.

Analyzing the Review Materials

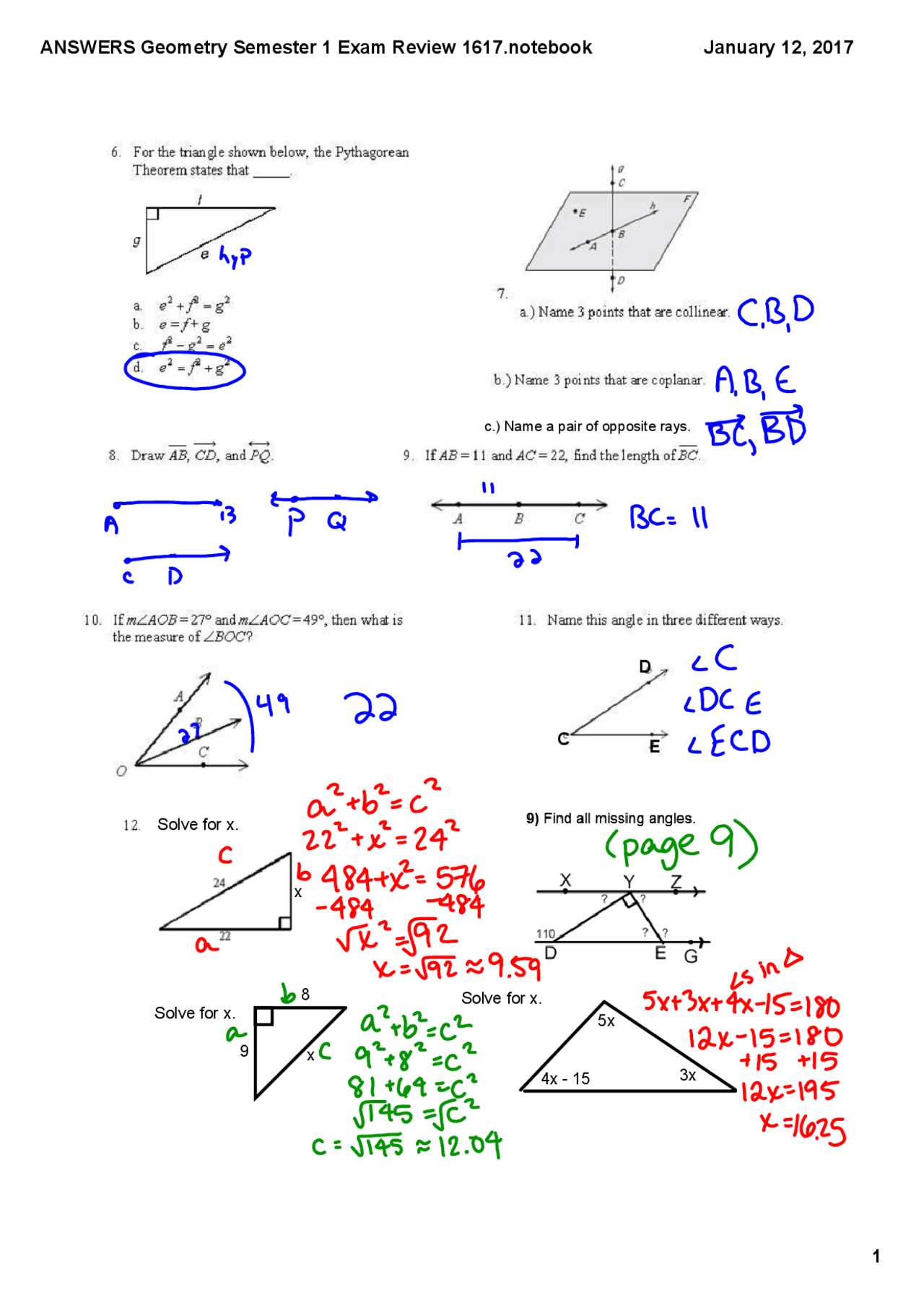
Effectively preparing for any assessment requires a careful examination of the review materials. These resources are designed to provide an overview of key concepts, highlight important problem-solving strategies, and offer practice opportunities to reinforce understanding. Analyzing the review materials helps identify areas of strength and weakness, enabling you to focus your efforts where they are most needed.

Start by organizing the review materials into categories, such as theorems, formulas, and problem types. This allows you to systematically review each section and ensure that no important concept is overlooked. Pay particular attention to the types of problems commonly featured in the materials, as they will give you insight into what to expect during the assessment.

Additionally, try to simulate real test conditions by practicing with timed exercises. This helps improve both speed and accuracy, ensuring you are prepared for the actual assessment. By analyzing and practicing with the review materials regularly, you will build confidence and be better equipped to tackle the most challenging problems.

How to Double-Check Your Solutions

Ensuring the accuracy of your solutions is an essential step in the problem-solving process. Double-checking your work allows you to verify that each calculation, reasoning step, and conclusion is correct. It helps identify any errors you might have overlooked and provides an opportunity to refine your approach before finalizing your results.

Here are some effective strategies for reviewing your work:

Revisit Key Steps: Go through each step of your solution and confirm that it follows logically from the previous one. Ensure that all necessary formulas and principles were correctly applied.
Check for Consistency: Verify that your results align with expected values or logical expectations. Inconsistencies often indicate a mistake that needs correction.
Use Alternative Methods: If possible, attempt the same problem using a different approach or method. A different perspective can help confirm the correctness of your solution.
Cross-Verify with Examples: Use sample problems or known solutions to verify the accuracy of your process. Comparing results can highlight discrepancies.

By applying these techniques, you can reduce the likelihood of mistakes and boost your confidence in your solutions. Taking the time to double-check your work is a simple yet highly effective way to ensure that your efforts reflect the highest level of accuracy and precision.

Strategies for Tackling Word Problems

Word problems often present unique challenges, requiring you to translate real-world scenarios into mathematical equations or logical steps. The key to solving these problems lies in carefully analyzing the text, identifying relevant information, and applying the appropriate techniques to find a solution. Developing a structured approach will make it easier to break down complex situations into manageable tasks.

Understanding the Problem

Before jumping into calculations, take the time to fully understand the problem. Read the problem carefully, paying close attention to the details and key pieces of information. Underline or highlight important data, such as numerical values and relationships between variables. This will give you a clear picture of what is being asked and how to proceed.

Setting Up the Equation

Once you understand the problem, translate the words into mathematical expressions. Identify the variables, constants, and operations involved. Think about how the given information relates to each other and set up an equation or system of equations that reflects this relationship. The goal is to turn the problem into something solvable using familiar methods.

Tip: If you’re stuck, break the problem down into smaller parts. Solve each part step-by-step before combining the results to reach the final answer.

Double-Checking Your Solution

After solving, always double-check your answer. Review the problem to ensure that all relevant information has been used and that your solution makes sense in the context. If the answer seems too large or too small, reassess your steps to identify any errors.

By following these strategies, you’ll develop the skills needed to confidently approach word problems, no matter how complex they may seem. Taking your time to analyze and methodically solve each part will help you arrive at the correct solution efficiently and accurately.

Maintaining Focus During the Exam

Staying focused during a test is essential to ensuring you can perform at your best. The pressure of time, the complexity of questions, and the variety of topics can all create distractions. However, managing your attention and maintaining a clear mindset throughout the test can significantly impact the quality of your responses and overall performance.

Preparation is Key: Before the test begins, ensure you are well-prepared and have a plan in place. Organize your materials, get enough rest the night before, and eat a balanced meal beforehand. A good mental and physical state will help you maintain focus when it matters most.

Effective Time Management

Managing your time wisely is one of the most effective ways to keep focus throughout the test. Allocate time to each section and stick to it. If you find yourself stuck on a particular question, move on and come back to it later. This ensures that you don’t waste valuable time on one problem and helps maintain momentum.

Staying Calm and Confident

It’s easy to feel anxious during a test, but staying calm is crucial for sustained focus. Practice deep breathing techniques or take brief moments to relax your mind. Confidence in your preparation will help you remain composed. Remind yourself that you are capable of solving the problems as you encounter them.

Tip: If your mind starts to wander, refocus by taking a brief mental break. Close your eyes for a few seconds, stretch, or take a deep breath to reset your concentration.

By implementing these strategies, you can ensure that you stay on task and complete the test efficiently. Focus, calmness, and preparation are your best allies in performing well under pressure.