Gradpoint Geometry B Answers Guide for Students

Mastering mathematical challenges often requires a clear approach and an understanding of the core principles. Whether you’re tackling complex calculations or solving visual problems, knowing how to break down each task is essential for success. This section provides valuable insights into how to approach various topics, offering guidance on how to effectively manage your assignments.

Effective strategies can significantly enhance your ability to complete tasks with accuracy. By grasping the underlying concepts, you’ll be better equipped to solve problems with confidence and efficiency. Solutions are not just about providing the right answers, but understanding the processes that lead to them.

Improving your skills is an ongoing process. By practicing regularly and utilizing available resources, you can gradually refine your approach and become more proficient in tackling even the most challenging problems. Keep honing your skills, and soon you’ll find that mathematical tasks become increasingly intuitive.

Gradpoint Geometry B Answers

Success in mathematical tasks requires a methodical approach to problem-solving. By understanding the basic principles and applying logical steps, students can confidently tackle a wide range of challenges. This section outlines key methods for navigating through assignments and finding the right solutions. With the right strategies, complex questions become more manageable and easier to understand.

Key Problem-Solving Techniques

Each task presents its own unique set of challenges, but certain techniques can be applied universally to simplify the process. Here are some essential strategies:

Carefully read the instructions before attempting any solutions.
Break the problem down into smaller, more manageable parts.
Use diagrams or visual aids to better understand spatial relationships.
Double-check all calculations for accuracy.
Apply relevant formulas as needed for each task.

Common Challenges and How to Overcome Them

While many students face difficulties during assignments, understanding common obstacles can help you avoid mistakes and stay on track. Some of the most frequent issues include:

Misinterpreting question wording, which can lead to incorrect answers.
Forgetting to apply the correct formula or equation.
Not taking enough time to review and verify your work.
Getting stuck on complex problems without knowing how to proceed.

By staying organized and using these tips, you can significantly improve your ability to complete each task efficiently and accurately.

Understanding Key Geometry Concepts

To excel in mathematical tasks that involve shapes, sizes, and spaces, it’s crucial to first grasp the foundational ideas that drive problem-solving. Recognizing the relationships between various elements allows for a clearer approach when tackling complex scenarios. This section highlights some of the most essential principles to help you navigate these tasks with ease.

Core Principles to Focus On

Before diving into intricate calculations, it’s important to have a solid understanding of a few basic concepts. These form the backbone of many mathematical problems:

Shapes and Figures: Understand the properties of basic shapes such as triangles, squares, and circles.
Angles: Learn the different types of angles, including acute, obtuse, and right angles.
Measurement: Familiarize yourself with units of measurement and how to calculate areas and perimeters.
Symmetry: Recognize how symmetry can simplify problem-solving, especially in geometric figures.

Common Tools and Formulas

Mastering the following tools and formulas is essential for solving many tasks:

Pythagorean Theorem: Useful for finding the length of a side in right triangles.
Area and Perimeter Formulas: Learn the specific formulas for various shapes.
Coordinate Plane: Understanding how to plot points and interpret graphs is key for spatial reasoning.
Trigonometric Ratios: These are important for solving problems related to angles and side lengths in triangles.

By mastering these core concepts, you’ll be well-equipped to approach more advanced topics with greater confidence and clarity.

How to Navigate Gradpoint Platform

Successfully using an online learning system requires familiarity with its layout and features. Understanding where to find key materials, track progress, and access assignments will enhance your ability to complete tasks efficiently. This guide will help you explore the platform’s structure and navigate through different sections with ease.

Key Features of the Platform

The platform offers several useful sections, each designed to support your learning process. Here is an overview of the primary features:

Section	Description
Dashboard	Shows an overview of your current tasks, upcoming deadlines, and progress reports.
Assignments	Where you can find all active tasks, submit work, and track feedback from instructors.
Resources	Provides study materials, reference guides, and additional help for completing assignments.
Grades	Allows you to review your performance and track progress throughout the course.

Efficient Navigation Tips

To make the most of your time on the platform, try the following tips:

Start with the Dashboard to get an overview of your current workload.
Regularly check the Assignments section for new tasks and deadlines.
Use the search function to quickly find materials or specific topics.
Stay organized by using the calendar tool to plan out your study schedule.

By understanding these key sections and tips, you’ll be able to move through the platform smoothly and stay on top of your work.

Tips for Solving Geometry Problems

Solving mathematical tasks that involve shapes and spatial relationships can be challenging, but with the right approach, you can improve your ability to tackle them effectively. By breaking down problems into smaller steps and using the right strategies, you can simplify even the most complex scenarios. This section offers practical tips to help you work through difficult problems with ease.

One of the first steps in solving any problem is to carefully read and understand the question. Take note of the given information and identify what is being asked. Visual aids, such as diagrams, can often clarify the relationships between different elements and help you see the problem from a new perspective.

Once you have a clear understanding of the problem, it’s time to apply the relevant concepts. This might involve using formulas, theorems, or basic principles such as symmetry and congruence. Here’s a set of tips to guide you through the process:

Draw Diagrams: Visualize the problem by sketching figures to identify key features and relationships.
Identify Known and Unknown Values: Mark the given information and determine what you need to find.
Use the Right Formula: Make sure to apply the correct formula for the shape or concept you’re dealing with.
Break the Problem into Parts: Divide the problem into smaller, manageable pieces and solve them step by step.
Check Your Work: After solving, review your steps to ensure accuracy and consistency.

By following these tips, you’ll be able to approach each task with a clear strategy and increase your chances of solving it correctly. Practice regularly to strengthen your skills and boost your confidence in handling various types of problems.

Common Mistakes in Geometry B

When working on spatial problems and measurements, it’s easy to make mistakes, especially when faced with complex calculations or unfamiliar concepts. Identifying common errors can help you avoid them and improve your overall problem-solving skills. In this section, we’ll explore some of the most frequent mistakes students make and how to prevent them.

Misinterpreting Problem Requirements

One of the most common mistakes is failing to understand what a problem is asking. Often, students rush through the instructions or overlook important details. This can lead to solving the wrong problem or missing out on critical steps.

Always read the problem carefully before beginning any calculations.
Highlight key information and write down what is being asked for.
Double-check the question to ensure you understand what needs to be solved.

Incorrect Application of Formulas

Another frequent error is applying the wrong formula or misusing one. Geometry problems often require specific formulas for different shapes and situations. Using the wrong one can lead to incorrect answers.

Ensure you’re using the right formula for the shape or type of problem you’re solving.
Write out the formula and check that all variables are correctly placed.
Don’t forget to review units of measurement and make sure they’re consistent throughout.

By being aware of these mistakes and taking the time to carefully read the instructions and apply the correct formulas, you can reduce the likelihood of errors and improve your problem-solving abilities.

Step-by-Step Solutions for Geometry B

Breaking down complex problems into manageable steps is a crucial skill when solving spatial and measurement-related tasks. A step-by-step approach allows you to stay organized and ensure that no detail is overlooked. This section provides a structured method for tackling problems, ensuring that each solution is approached logically and systematically.

Approach to Solving Problems

When faced with a new problem, follow these steps to ensure clarity and accuracy in your solution:

Read the Problem Carefully: Understand the question and identify the information provided.
Draw a Diagram: Visual representation helps clarify the relationships between different elements.
Identify Known and Unknown Values: Make note of what you already know and what you need to find.
Choose the Appropriate Formula: Select the formula that best fits the problem you are working on.
Substitute Values and Solve: Plug in the known values and perform the necessary calculations.
Double-Check Your Work: Verify each step to ensure all calculations are accurate and consistent.

Example Problem Breakdown

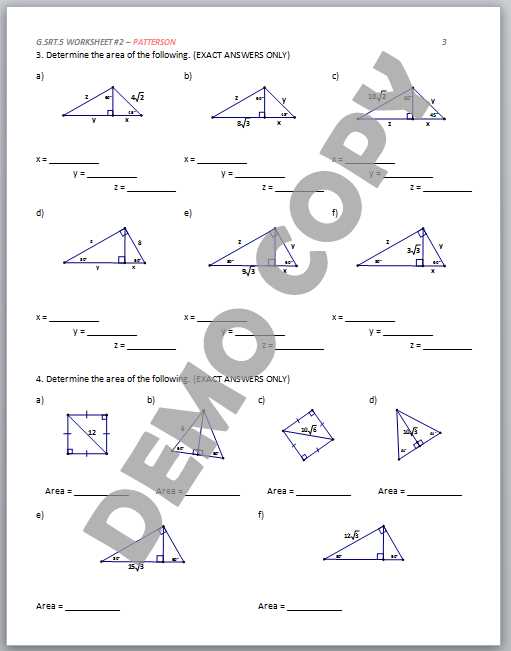
Let’s go through an example to demonstrate this step-by-step approach:

Problem: Find the area of a circle with a radius of 5 units.
Step 1: Read the problem and identify that you need to find the area of a circle.
Step 2: Draw a circle and label the radius as 5 units.
Step 3: Use the formula for the area of a circle: A = πr².
Step 4: Substitute the value of the radius: A = π(5)² = 25π.
Step 5: The area is approximately 78.54 square units (using π ≈ 3.1416).
Step 6: Double-check that the formula was used correctly and calculations are accurate.

By following these steps, you can confidently solve a wide range of problems and ensure accurate results every time.

How to Prepare for Geometry B Tests

Preparing for a test that involves shapes, measurements, and spatial reasoning requires a strategic approach. By organizing your study time, reviewing key concepts, and practicing problem-solving, you can build confidence and improve your performance. This section outlines effective strategies to help you succeed on upcoming assessments.

Key Preparation Strategies

To perform well on any test, it’s essential to focus on understanding the core concepts and developing the necessary skills. Here are some useful strategies:

Review Notes Regularly: Go through your class notes to refresh your memory on the topics covered in class.
Practice Problems: Solve a variety of problems to apply what you’ve learned and reinforce your understanding.
Understand Formulas: Memorize key formulas and understand when and how to use them correctly in different situations.
Use Study Guides: Refer to any provided study guides or materials that summarize the most important concepts.
Ask Questions: If there’s anything unclear, don’t hesitate to ask your teacher or peers for clarification.

Effective Study Tips

In addition to reviewing materials, the following tips can help maximize your study efficiency:

Break Study Sessions into Chunks: Focus on one topic at a time and take breaks between study sessions to avoid burnout.
Teach Someone Else: Teaching a concept to someone else can solidify your understanding and reveal any gaps in your knowledge.
Practice with Timed Tests: Simulate test conditions by timing yourself while solving practice problems.
Stay Positive: A positive mindset helps reduce anxiety and allows you to focus on solving problems more effectively.

By following these strategies and incorporating them into your study routine, you can be well-prepared to tackle any challenges that may come your way during the test.

Improving Your Geometry Skills

Enhancing your ability to solve problems involving shapes, space, and measurements requires practice, understanding, and the application of key principles. Whether you’re new to this subject or looking to refine your skills, there are effective ways to improve. In this section, we will explore practical methods and strategies that can help you strengthen your abilities and approach challenges with confidence.

Effective Practice Techniques

To improve your skills, consistent practice is essential. The more you practice, the more familiar you become with the concepts and techniques necessary for solving problems. Below are some helpful strategies:

Practice with Real Problems: Solve a variety of problems regularly to apply the concepts you have learned.
Focus on Weak Areas: Identify areas where you struggle and dedicate extra time to understanding those concepts.
Review Mistakes: After solving a problem, review any mistakes to understand why the solution didn’t work and how to correct it.
Work with Others: Collaborating with classmates or a tutor can provide new insights and help you understand difficult topics.

Utilizing Resources Effectively

Using available resources to their full potential can significantly boost your learning. These resources include textbooks, online tools, and practice tests. Here’s how to make the most of them:

Resource	How to Use It
Textbooks	Use your textbook for detailed explanations, examples, and exercises that reinforce key concepts.
Online Tools	Take advantage of interactive tools, videos, and quizzes to deepen your understanding.
Practice Tests	Simulate exam conditions by completing timed practice tests to improve speed and accuracy.

By consistently applying these strategies and utilizing resources effectively, you will gradually improve your skills and gain confidence in solving even the most complex problems.

How Gradpoint Geometry Affects Grades

Mastering complex concepts in space, shape, and measurement can significantly impact overall academic performance. How well students understand these concepts can influence not only their test scores but also their ability to apply knowledge in real-world situations. This section examines the connection between mastery of spatial reasoning and its direct effect on grades, offering insights into how students can improve their outcomes.

Impact of Understanding Core Concepts

When students grasp the foundational concepts in spatial reasoning, it improves their performance across various assessments. Here’s how a strong understanding can affect grades:

Improved Test Performance: A solid understanding allows for quicker problem solving and better accuracy during tests, which can raise scores.
Better Application of Knowledge: Mastery of the subject allows students to apply concepts in a variety of problem types, leading to higher success rates.
Increased Confidence: Confidence in solving spatial problems leads to better classroom participation and a more positive learning experience, which can enhance grades.

Effect on Long-Term Academic Success

The ability to apply spatial reasoning and measurement skills goes beyond just grades. It can contribute to a stronger foundation for future learning and academic success. Consider the following:

Benefit	How it Impacts Grades
Critical Thinking Skills	Mastering complex problems enhances students’ critical thinking, which helps in all subjects and positively impacts their overall GPA.
Preparation for Advanced Topics	Strong skills in spatial reasoning prepare students for more advanced topics in science, technology, and engineering, ensuring better performance in future courses.
Increased Motivation	When students see improvement in their grades due to their hard work, it boosts motivation to continue excelling.

By focusing on mastering core skills, students can improve both their grades and their ability to apply knowledge effectively in various contexts, setting them up for future academic success.

Using Online Resources for Geometry Help

With the growing availability of digital learning tools, students can now access a wealth of information to help them master spatial reasoning and related subjects. Online resources can offer explanations, practice problems, and interactive lessons that cater to different learning styles. This section explores how students can make the most of these resources to enhance their understanding and boost their academic performance.

Advantages of Online Learning Platforms

Online platforms offer flexibility and a range of learning materials that can complement traditional classroom instruction. Here are some key benefits:

24/7 Access: You can access materials and tutorials at any time, making it easier to fit study sessions around your schedule.
Interactive Tools: Many platforms offer interactive lessons and quizzes that provide instant feedback, allowing you to track your progress.
Diverse Learning Styles: Whether you prefer watching video tutorials, reading articles, or solving problems, there are resources tailored to various learning preferences.
Step-by-Step Guidance: Some platforms offer detailed step-by-step solutions that can help you understand how to approach complex problems.

Recommended Online Resources

There are several reputable online platforms that offer valuable help for mastering spatial concepts. Here are some suggestions:

Khan Academy: Offers free video lessons, exercises, and quizzes on various topics related to spatial reasoning and measurement.
IXL: Provides interactive practice problems and personalized learning paths to help you improve your skills in a structured way.
Coursera: Hosts online courses taught by university professors, covering advanced topics in mathematics and spatial problem-solving.
Wolfram Alpha: Useful for checking your solutions and exploring step-by-step explanations for various types of problems.

By integrating these resources into your study routine, you can reinforce your understanding, practice problems in new ways, and gain a deeper appreciation for the subject.

Geometry B Question Types Explained

Understanding the various types of questions encountered in spatial reasoning assessments is essential for effective preparation. These questions are designed to test not only your ability to recall facts but also your capacity to apply logical thinking and problem-solving strategies. In this section, we’ll explore the common types of questions you’ll encounter and strategies for tackling each one.

Multiple-Choice Questions

Multiple-choice questions are a common format in assessments, testing your knowledge of key concepts and your ability to apply them to solve problems. Here’s what you need to know:

Focus: These questions often test your ability to identify correct information or select the most appropriate method for solving a problem.
Strategy: Eliminate obviously incorrect answers first, then evaluate the remaining options carefully to determine the best fit.
Tip: Pay attention to subtle wording differences in options–sometimes the phrasing of a question can be tricky.

Problem-Solving and Application Questions

These types of questions require you to apply your understanding to solve more complex problems. They often involve step-by-step solutions and require logical reasoning to arrive at the correct answer.

Focus: Applying learned concepts to solve practical problems, such as calculating areas, volumes, or angles.
Strategy: Break down the problem into smaller, manageable steps, and carefully organize your work to avoid errors.
Tip: Practice solving similar problems to build confidence and efficiency in applying the correct methods.

By becoming familiar with these question types and practicing appropriate strategies, you can improve your ability to tackle problems effectively and confidently during assessments.

Time Management for Geometry Assignments

Effective time management is a crucial skill when tackling mathematical tasks, especially when dealing with complex problems that require careful attention to detail. Properly allocating time for each assignment ensures that you can complete your work efficiently and with the highest level of accuracy. This section offers practical tips to help you manage your time better and improve your performance.

Prioritizing Tasks

Not all assignments are created equal. Some tasks may require more time and focus, while others can be completed more quickly. To optimize your study time, consider the following:

Assess Complexity: Begin with the more challenging problems or assignments that require the most time. This ensures that you tackle the hardest tasks while your mind is fresh.
Break Tasks into Steps: Divide larger tasks into smaller, more manageable chunks. This prevents feeling overwhelmed and allows you to track your progress more easily.
Set Milestones: Establish short-term goals for each session to keep yourself motivated and focused.

Utilizing Study Blocks

Using structured study blocks can help you stay on track and maintain concentration. Here are some tips for creating effective study sessions:

Work in Intervals: Use techniques like the Pomodoro method, where you work for 25 minutes followed by a short break. This helps maintain focus while avoiding burnout.
Limit Distractions: Set up a quiet study environment, free from distractions like social media or noise, to ensure maximum productivity during each study block.
Review Regularly: Set aside time each week to review completed assignments and assess areas where you can improve. Regular revision reinforces learning and minimizes cramming before deadlines.

By following these strategies, you can maximize your efficiency, reduce stress, and achieve better results in your assignments. Effective time management will not only help you stay on top of your workload but also give you more time to focus on mastering the subject matter.

How to Review Geometry B Answers

Reviewing your work is a critical step in mastering complex mathematical concepts. By carefully checking your solutions, you not only ensure that your answers are accurate but also reinforce your understanding of the methods used. This section provides strategies for reviewing your work effectively to enhance your problem-solving skills and avoid common errors.

Steps for Thorough Review

Following a systematic approach when reviewing your solutions can help you catch mistakes and improve your understanding. Here are some effective steps to take:

Revisit the Question: Before checking your solution, re-read the question carefully to ensure you fully understand what is being asked. This helps clarify any potential misunderstandings.
Verify Each Step: Go through each step of your solution one by one, checking for any miscalculations or skipped procedures. Ensure that every calculation and logic used is correct.
Check for Unit Consistency: Pay attention to units (e.g., centimeters, degrees, etc.). Verify that the units are consistent throughout the problem and the final answer matches the required format.

Common Mistakes to Look For

Being aware of typical errors can help you avoid repeating them. Below are some common pitfalls to watch for:

Sign Errors: Negative signs are often overlooked, especially when dealing with subtraction or coordinates. Always double-check your signs to avoid errors.
Incorrect Formula Application: Ensure you are using the correct formulas for the specific problem. Sometimes, students mistakenly apply a formula meant for a different situation.
Rounding Errors: In problems that require approximation, double-check your rounding. Ensure that you rounded to the appropriate number of decimal places as instructed.

By following these steps and being mindful of common mistakes, you can significantly improve the accuracy of your solutions and strengthen your grasp of the material. Reviewing your work with attention to detail is a valuable habit that will pay off in both accuracy and confidence.

Strategies for Geometry B Success

Achieving success in mathematical subjects requires more than just completing assignments; it involves mastering the underlying concepts, honing problem-solving techniques, and applying effective study habits. This section outlines key strategies that can help you excel in mathematical coursework, improve your understanding, and boost your performance on assessments.

Effective Study Habits

Developing strong study habits is essential for mastering challenging material. Consistent effort and proper time management are critical. Here are a few tips to enhance your study routine:

Set a Regular Study Schedule: Designate specific times each day for focused study. Consistency helps reinforce learning and reduces procrastination.
Break Down Complex Topics: Large topics can seem overwhelming. Break them down into smaller, manageable sections and tackle one concept at a time.
Practice Regularly: Frequent practice is key to retaining new knowledge. Solve a variety of problems to strengthen your understanding and problem-solving skills.

Approaching Problem-Solving

Mastering problem-solving skills is fundamental to success in mathematics. Here’s how you can approach each problem effectively:

Understand the Problem: Before jumping into calculations, read the problem carefully. Identify the known values, what needs to be found, and the relationships between them.
Use Diagrams: Visual aids like graphs, diagrams, or drawings can help clarify complex concepts and provide a better understanding of the problem.
Work Step-by-Step: Break the problem into smaller steps and solve each part methodically. Avoid skipping steps, as this can lead to errors.

By implementing these strategies, you will not only improve your grades but also develop a deeper understanding of the material. Consistent practice, effective study techniques, and a structured approach to problem-solving will ensure success in your studies.

Understanding Geometry B Assignment Structure

In many math-related courses, assignments are designed to evaluate understanding and reinforce key concepts. These tasks typically follow a clear structure, helping students to develop critical problem-solving skills. Understanding how these assignments are organized is crucial for managing time effectively and completing them successfully.

Assignments are often divided into sections based on specific topics or types of problems. Each section serves a particular purpose, guiding the student through different stages of learning. Familiarizing yourself with the structure can help you focus your efforts and avoid feeling overwhelmed.

Common Assignment Breakdown

Assignments may consist of a series of steps or individual questions, each requiring a different approach. Below is a typical breakdown of how tasks are organized:

Section	Purpose	Focus Areas
Introduction	Overview of the concepts covered in the assignment.	Basic definitions, key principles, and context.
Practice Problems	Application of concepts to specific scenarios.	Step-by-step solutions, formulas, and strategies.
Review Questions	Test understanding and ensure retention of knowledge.	Critical thinking, connections between topics.
Challenges	Test higher-level problem-solving abilities.	Advanced techniques and complex problem-solving.

Each part of the assignment serves a purpose in helping you understand and apply mathematical concepts. By breaking tasks down into manageable sections and tackling them one at a time, you can approach assignments with confidence and clarity.

FAQs about Geometry B

When tackling complex subjects, students often have a variety of questions about course materials, assignments, and assessments. Understanding common concerns can help clarify any doubts and provide direction for more effective studying. Below, you’ll find answers to some frequently asked questions about this particular subject.

What topics are covered in the course?

The course typically includes a variety of topics related to spatial reasoning, properties of shapes, measurements, and relationships between angles, lines, and surfaces. Understanding the core concepts is essential for successfully navigating the coursework.

How can I improve my performance?

Consistent practice and mastering foundational concepts are key. Additionally, breaking down complex problems into smaller steps and seeking clarification when needed can greatly improve your understanding and performance in assessments.

Are there additional resources available for help?

Yes, there are many online platforms and textbooks available to provide extra practice and tutorials. Utilizing these resources can help reinforce difficult concepts and offer additional explanations outside of class.

What is the best way to prepare for assessments?

Focus on understanding the key principles, practicing sample problems, and reviewing past assignments. It’s also helpful to join study groups where concepts can be discussed and clarified. Proper time management will also ensure you are well-prepared for tests.

What should I do if I don’t understand a problem?

If you’re struggling with a problem, don’t hesitate to break it down into smaller parts. Review your notes and try working through similar examples. If the problem persists, asking for assistance from a teacher or tutor can provide clarity.