
Geometry Mastery Test Preparation Solutions
In this section, we will explore the essential concepts and strategies needed to succeed in a comprehensive assessment of spatial reasoning and mathematical principles. The focus will be on key techniques that will help you understand the types of problems you may encounter and how to approach them effectively. With the right methods and problem-solving skills, mastering these topics becomes a manageable and rewarding task.
Key Concepts and Problem-Solving Strategies
Understanding the core principles behind geometric shapes, their properties, and relationships is crucial. By practicing with various examples, you can sharpen your ability to identify patterns, apply formulas, and solve problems more efficiently. Focus on areas such as transformations, theorems, and calculations involving angles, areas, and volumes.
Effective Review Methods
One of the most effective ways to prepare is to work through sample exercises that mirror the format of the test. This helps familiarize you with the problem types and timing. Additionally, reviewing notes, engaging in study groups, and practicing under timed conditions can significantly improve confidence and performance.
Key Concepts to Master for Success

Mastering the fundamental ideas and strategies in spatial reasoning is crucial for achieving success in any mathematical assessment. These core topics form the backbone of the subject and are essential for solving complex problems efficiently. By developing a deep understanding of these concepts, you can build a strong foundation for tackling various challenges that arise in related areas.
Focus on understanding shapes, their properties, relationships, and how to manipulate them. Practice solving problems that involve transformations, measurements, and logical reasoning. By becoming familiar with these key principles, you’ll be better equipped to handle a wide range of questions and problem types.
Essential Formulas for Mathematical Assessments

To excel in tests that focus on spatial reasoning, it is important to be familiar with the key equations and principles that govern various shapes and their properties. Mastering these formulas allows you to quickly solve problems involving measurements, transformations, and calculations. By applying these fundamental tools effectively, you can improve both accuracy and speed during your preparation.
Formulas for Perimeter and Area
One of the most frequently encountered tasks involves finding the perimeter and area of different shapes. These calculations are foundational, and knowing the specific formulas for each type–such as squares, rectangles, triangles, and circles–will significantly boost your problem-solving capabilities. For example, the area of a rectangle is calculated by multiplying its length and width, while the area of a circle requires the use of pi and the square of its radius.
Volume and Surface Area Equations

When dealing with three-dimensional objects, it’s essential to understand the formulas for volume and surface area. For example, the volume of a cylinder is calculated using the formula πr²h, where r is the radius and h is the height. Likewise, the surface area of a sphere requires the formula 4πr². Familiarity with these equations ensures you can handle a variety of 3D shape-related problems with ease.
Tips for Tackling Spatial Reasoning Word Problems

Word problems in mathematics often combine real-world scenarios with abstract concepts, requiring a structured approach to solve. The key to success is breaking down the information systematically, identifying relevant details, and applying the right methods to arrive at a solution. Developing a strategy for interpreting and solving these problems will help you navigate complex questions with confidence and accuracy.
Understanding the Problem and Identifying Key Information
Before jumping into calculations, carefully read the problem and highlight important values, shapes, and relationships. Often, word problems provide extra details that are not directly necessary for solving the task. Focus on the core elements and translate them into mathematical terms. This will give you a clear starting point for applying the appropriate formulas or strategies.
Creating a Visual Representation
One effective technique is to sketch a diagram or chart that represents the scenario described in the problem. This visual aid can help clarify the relationships between different elements and make it easier to identify the steps needed for a solution. A diagram can also help prevent misinterpretation of the given data, ensuring you apply the correct formulas.
Understanding Proofs Efficiently
Mastering logical reasoning and argumentation is essential for solving many types of problems. Proofs require a structured approach, where each step builds upon the previous one to establish the truth of a given statement. By developing a clear strategy for tackling proofs, you can improve both the speed and accuracy of your solutions, ensuring that you can confidently work through complex problems.
Breaking Down the Statement
The first step in tackling any proof is to fully understand the statement you’re trying to prove. Carefully analyze the given information and the conclusion you’re attempting to reach. Identify any properties or relationships that might be useful, and determine how they relate to one another. This foundational understanding will guide the steps of your proof.
Logical Steps and Justifications
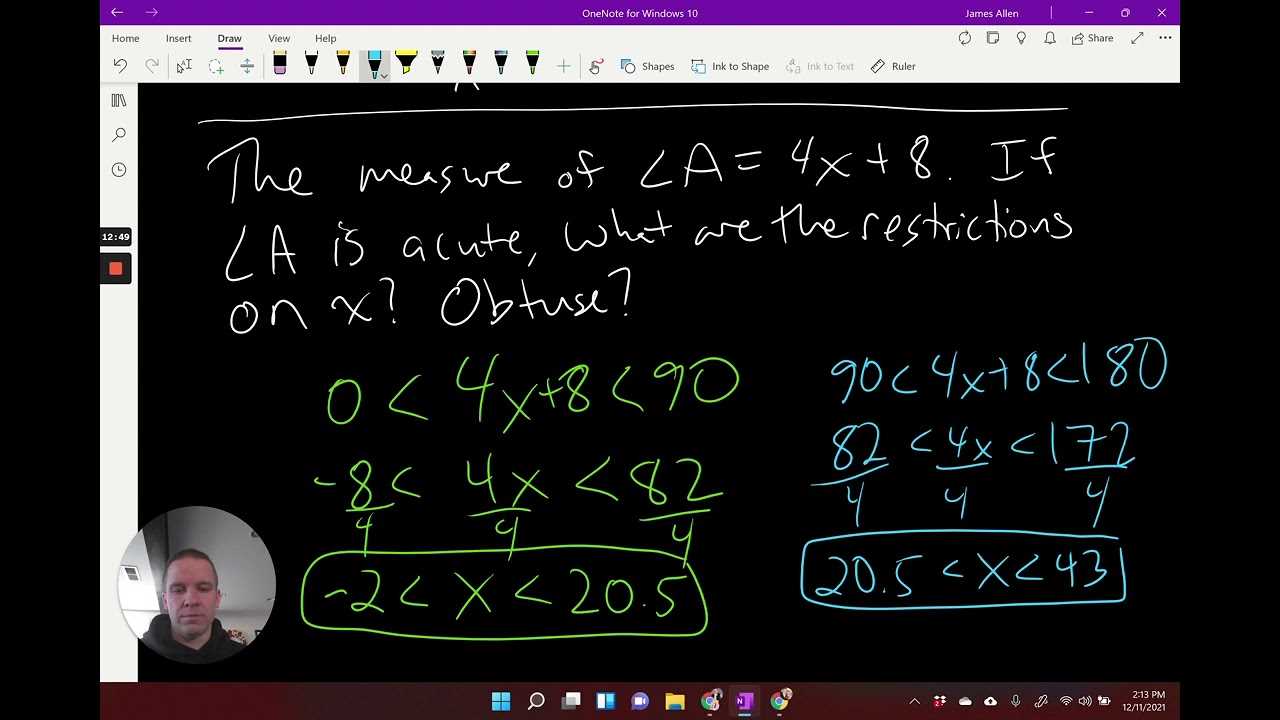
Once you’ve identified the necessary elements, begin constructing your argument by applying known theorems, definitions, and properties in a logical sequence. Ensure each step is justified, clearly explaining why one step leads to the next. By following a logical flow, you can make the proof more comprehensible and easier to follow, while demonstrating the validity of your conclusion.
Common Mistakes to Avoid During the Test
During a challenging assessment, it’s easy to overlook certain details or rush through problems, which can lead to avoidable errors. Recognizing common pitfalls and adopting a careful approach can significantly improve your performance. By being mindful of these frequent mistakes, you can ensure a more accurate and efficient test-taking experience.
Rushing Through Problems is one of the most common errors. While time management is important, speeding through questions without fully understanding them can lead to mistakes. Take a moment to read each question carefully and plan your approach before jumping into calculations or reasoning.
Misinterpreting Given Information can also cause problems. Always pay attention to specific details such as measurements, units, and relationships between elements. Missing small but crucial pieces of information can lead to incorrect solutions. Ensure that you interpret the data accurately and refer back to the question if necessary.
Forgetting to Check Your Work is another key mistake. Even if you’re confident in your answers, it’s vital to review your work before finishing. Errors often become apparent upon a second look, and correcting them before submission can improve your overall score.
Step-by-Step Solutions for Complex Questions
When faced with challenging problems, breaking down each step is essential for finding the correct solution. Complex tasks can often seem overwhelming, but by following a structured process and addressing each part systematically, you can solve them more effectively. This methodical approach ensures that all aspects of the problem are covered and that you arrive at the right conclusion with clarity.
Understanding the Problem
Before jumping into calculations, it’s crucial to understand all the given information. Look for key values, shapes, or relationships that will help guide your solution. By identifying these elements early on, you can avoid confusion and stay focused on the critical aspects of the problem.
Step-by-Step Approach
Once the problem is clearly understood, break it down into manageable steps. Here is an example of how to approach a complex question:
| Step | Action | Explanation |
|---|---|---|
| 1 | Identify given values | Determine which information is provided in the question, such as dimensions or angles. |
| 2 | Choose the appropriate formula | Select the formula or theorem that applies to the situation (e.g., Pythagorean Theorem, area formulas). |
| 3 | Perform the calculation | Carry out the necessary mathematical operations, paying attention to units and accuracy. |
| 4 | Double-check results | Review your solution to ensure all steps were followed correctly and there are no errors. |
Time Management Strategies for Mathematical Assessments
Effective time management is crucial for tackling complex mathematical tasks, especially when dealing with problems that require careful calculations and logical reasoning. By organizing your time wisely, you can ensure that you address every question thoroughly while avoiding unnecessary stress. Implementing a strategy that balances speed and accuracy will help you perform at your best during any time-constrained task.
Planning Your Approach
Before you begin, take a few minutes to plan how you will allocate your time. Here are some steps to help you manage your time effectively:
- Assess the total time available: Determine how much time you have and divide it by the number of questions to get a rough idea of how long to spend on each one.
- Prioritize the questions: Start with the problems that you find easiest, as this will build your confidence and ensure you don’t waste time on questions you can easily solve.
- Keep track of time: Use a watch or clock to monitor your progress. If you’re spending too much time on one question, move on and return to it later if necessary.
Handling Difficult Questions
Sometimes, certain questions may prove to be more challenging. Here’s how to handle them without wasting too much time:
- Don’t panic: Take a deep breath and focus on what’s being asked. Often, a calm mind can solve problems more efficiently than rushing.
- Skip and return: If a question is taking too long, move on to the next one and come back to the difficult one after completing the easier tasks.
- Check your work: Once you’ve completed all questions, use any remaining time to double-check your answers and ensure accuracy.
How to Approach Diagrams Effectively

Diagrams are often an essential part of mathematical problems, helping to visualize relationships and simplify complex situations. Understanding how to interpret these visual aids is key to solving problems accurately. By analyzing diagrams carefully, you can extract crucial information that guides your solution process and enhances your understanding of the question.
Step 1: Identify Key Elements
Before attempting to solve any problem, examine the diagram for important elements such as angles, lines, shapes, and labels. These components often contain the necessary information to apply formulas or theorems.
- Look for labeled points: Identify any points or vertices that are marked with letters or numbers, as they can represent known values.
- Examine geometric shapes: Recognize the shapes in the diagram (triangles, circles, squares, etc.) and recall relevant properties.
- Check for given measurements: Take note of any angles, side lengths, or other values provided in the diagram.
Step 2: Translate Visual Information into Mathematical Terms
Once you’ve identified the key elements in the diagram, the next step is to translate this visual information into mathematical expressions or equations. This helps connect the diagram to the question and allows you to apply the appropriate formulas.
- Label the diagram: If not already labeled, add any necessary measurements or angles to the diagram to clarify relationships between the elements.
- Use symbols for unknowns: Assign variables to unknown values in the diagram, making it easier to set up equations for solving.
- Look for patterns: Identify any symmetrical or proportional relationships between the elements that can simplify the problem-solving process.
Mastering Coordinate Concepts for Assessments
Understanding the relationship between algebra and geometry is key to solving problems that involve points, lines, and shapes on a coordinate plane. Mastery of this area requires a clear grasp of formulas, concepts, and strategies for translating geometric ideas into algebraic expressions. With the right approach, you can confidently solve complex problems involving distances, midpoints, slopes, and equations of lines.
Key Formulas to Remember
In coordinate-based problems, certain formulas are essential for finding distances, slopes, and midpoints. These foundational tools allow you to quickly translate between visual information and mathematical expressions.
- Distance Formula: Use this to find the distance between two points, ( d = sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} ).
- Midpoint Formula: This formula gives the midpoint of a line segment between two points, ( M = left( frac{x_1 + x_2}{2}, frac{y_1 + y_2}{2} right) ).
- Slope Formula: To determine the slope of a line, use ( m = frac{y_2 – y_1}{x_2 – x_1} ).
Strategies for Solving Problems
Applying these formulas effectively requires a systematic approach to problem-solving. Follow these strategies to ensure you’re on the right track:
- Plot the points: Visualizing the points on a coordinate plane can help you understand the relationships between them, especially for distance and slope problems.
- Identify known values: Carefully identify the coordinates of points or other key values provided in the question before applying any formulas.
- Check for special cases: Be aware of vertical or horizontal lines (undefined slope or zero slope) and special points like the origin.
Exploring Triangle Properties in Depth
Triangles are fundamental shapes in mathematics, with properties that reveal essential relationships between angles, sides, and other elements. Understanding these properties allows for solving complex problems and deriving key results in various contexts. By exploring different types of triangles and their unique characteristics, you can gain deeper insights into how they behave and how to approach them in problem-solving scenarios.
Types of Triangles and Their Characteristics
Triangles can be categorized based on their sides or angles, each type offering specific properties that are crucial for solving related problems.
- Equilateral triangle: All three sides and angles are equal, with each angle measuring 60 degrees.
- Isosceles triangle: Two sides are of equal length, and the angles opposite these sides are also equal.
- Scalene triangle: All sides and angles have different measures.
- Right triangle: One of the angles is 90 degrees, allowing the application of the Pythagorean theorem.
- Acute and obtuse triangles: Acute triangles have all angles less than 90 degrees, while obtuse triangles have one angle greater than 90 degrees.
Key Theorems and Formulas
Several theorems and formulas are essential for working with triangles, particularly in solving for unknown sides, angles, or areas.
- Pythagorean Theorem: Used for right triangles, it states that (a^2 + b^2 = c^2), where (c) is the hypotenuse.
- Triangle Sum Theorem: The sum of the interior angles of any triangle is always 180 degrees.
- Area of a triangle: The area can be calculated using the formula ( A = frac{1}{2} times text{base} times text{height} ).
Key Theorems Every Student Should Know
Mathematical reasoning is built on a foundation of fundamental principles that help in solving various types of problems. These core theorems provide the structure necessary to understand complex relationships between figures, angles, and lengths. Mastery of these theorems is crucial for anyone working through geometry-related questions, as they serve as the building blocks for most problem-solving techniques.
Here are some of the most important theorems that every student should be familiar with:
- Pythagorean Theorem: This theorem applies to right-angled triangles and states that the square of the hypotenuse is equal to the sum of the squares of the other two sides, (a^2 + b^2 = c^2).
- Angle Sum Theorem: In any triangle, the sum of the interior angles is always 180 degrees. This is a foundational rule for understanding triangle properties.
- Parallel Line Theorem: When two parallel lines are cut by a transversal, corresponding angles are congruent, alternate interior angles are congruent, and consecutive interior angles are supplementary.
- Congruence Postulates: These are used to determine if two triangles are congruent. Key postulates include Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA).
- Similar Triangles Theorem: Two triangles are similar if their corresponding angles are congruent and the lengths of corresponding sides are proportional.
Strategies for Tackling Multiple-Choice Questions
Multiple-choice questions require a different approach compared to open-ended problems. When dealing with these types of questions, it’s essential to focus on recognizing patterns, eliminating incorrect options, and applying your understanding of key principles. By approaching each question systematically, you can significantly improve your chances of selecting the correct answer, even when you’re uncertain at first.
Effective Strategies
Here are some useful strategies to maximize your performance on multiple-choice questions:
- Eliminate clearly wrong answers: Often, some answer choices will be obviously incorrect. Cross these out first to narrow down your options.
- Look for familiar patterns: Many questions will test similar concepts. Once you recognize the concept being tested, quickly recall the associated formula or theorem.
- Check for common mistakes: Some options may contain common errors (like misapplication of formulas or misinterpretation of the question). Be mindful of these and avoid them.
- Estimate when in doubt: If you are unsure, use estimation or approximation to eliminate some of the options. For example, approximate values or estimate distances if the exact answer is hard to calculate.
- Read all options: Even if one option looks correct, it’s important to review all choices. Sometimes, a better answer might be present that requires a more thorough understanding.
Example of a Multiple-Choice Question
Below is an example of how to apply the above strategies:
| Question | Choices |
|---|---|
| What is the area of a triangle with a base of 10 units and height of 5 units? | A) 25 units² B) 50 units² C) 30 units² D) 20 units² |
Strategy: The area of a triangle is calculated using the formula (A = frac{1}{2} times text{base} times text{height}). Using this formula, ( A = frac{1}{2} times 10 times 5 = 25). Therefore, the correct answer is A.
Reviewing Transformations and Symmetry
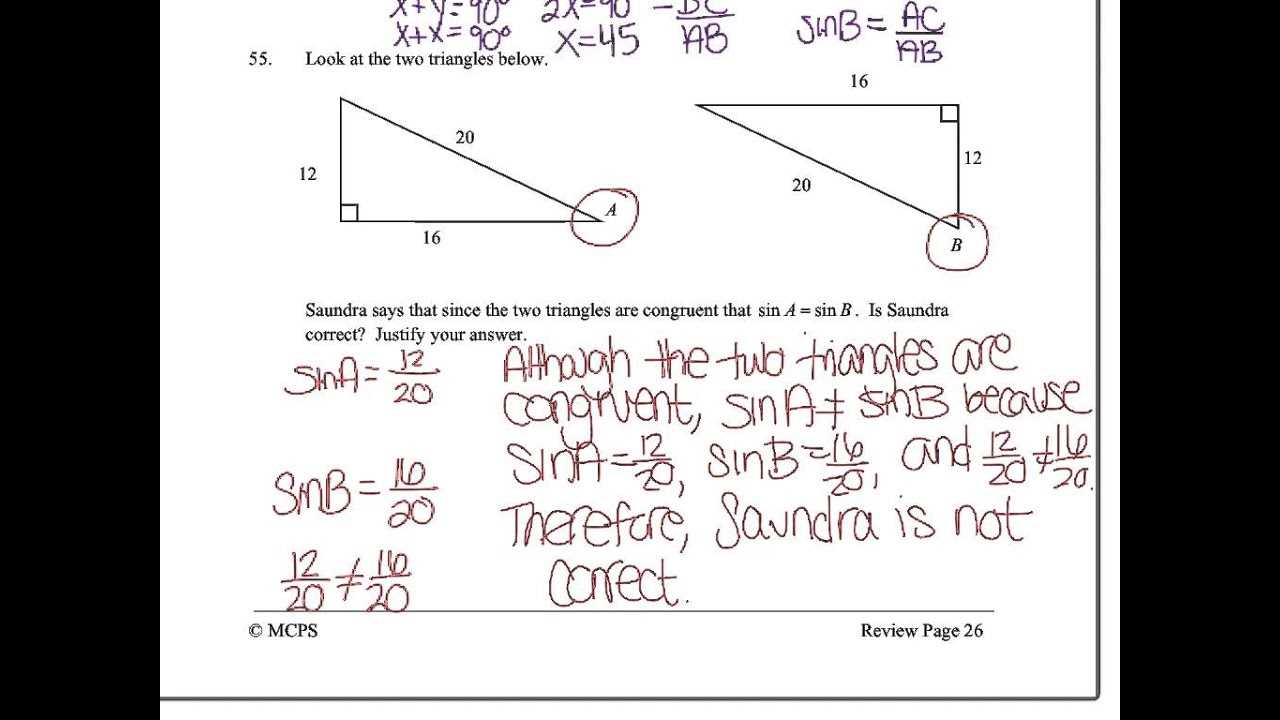
Understanding how shapes and figures can be altered without changing their core properties is essential in mastering spatial reasoning. Transformations and symmetry allow us to explore the relationships between objects, both in terms of their movement and their structural balance. These concepts help in recognizing patterns, solving problems, and interpreting geometric figures in various contexts.
Types of Transformations
Transformations involve moving, rotating, reflecting, or resizing figures. Each transformation has its own rules and characteristics:
- Translation: This involves sliding a figure from one position to another without changing its shape or size.
- Rotation: A figure is turned around a fixed point by a certain angle.
- Reflection: A figure is flipped over a line, creating a mirror image of the original shape.
- Dilation: This transformation resizes a figure, making it larger or smaller while maintaining its shape’s proportions.
Symmetry in Shapes
Symmetry refers to the balanced arrangement of parts of a figure. A shape exhibits symmetry if one part can be transformed into another part through a specific operation, such as rotation or reflection. Common types of symmetry include:
- Line symmetry: A shape has line symmetry if it can be folded along a line such that both halves match exactly.
- Rotational symmetry: A figure has rotational symmetry if it can be rotated by a certain angle and still match its original position.
- Point symmetry: A figure has point symmetry if every part of the figure has a matching part at an equal distance from a central point.
Understanding Circles and Their Properties
Circles are fundamental shapes in mathematics, known for their perfect symmetry and unique properties. They appear in many areas of study, from basic geometry to advanced applications in trigonometry and calculus. By understanding the key features of circles, such as their radius, diameter, and the relationships between various segments, students can solve problems involving angles, arc lengths, and areas with ease.
Key Elements of a Circle
A circle consists of several important components that define its structure:
- Center: The point equidistant from all points on the circle.
- Radius: The distance from the center of the circle to any point on its circumference.
- Diameter: A line segment passing through the center of the circle and connecting two points on the circumference. It is twice the length of the radius.
- Circumference: The perimeter or boundary of the circle. It is calculated using the formula ( C = 2 pi r ), where ( r ) is the radius.
- Area: The space enclosed by the circle. The formula for the area is ( A = pi r^2 ).
Properties and Theorems Involving Circles
Circles have several important properties that govern their behavior in geometric problems:
- Chord: A line segment that connects two points on the circle’s circumference. A diameter is a special type of chord that passes through the center.
- Arc: A part of the circumference of the circle. Arcs can be measured in degrees, and the length of an arc is proportional to the central angle that subtends it.
- Central Angle: An angle whose vertex is at the center of the circle and whose sides intersect the circle’s circumference.
- Inscribed Angle: An angle whose vertex lies on the circle and whose sides are chords of the circle. The measure of an inscribed angle is half the measure of the central angle subtended by the same arc.
Preparing for Advanced Geometry Problems
Successfully tackling complex mathematical challenges requires a strong foundation in core concepts and the ability to apply them in various situations. As problems become more intricate, understanding the underlying principles and developing problem-solving strategies becomes essential. Advanced problems often require critical thinking, pattern recognition, and a deeper understanding of relationships between shapes and figures.
Key Skills to Develop
To excel in more challenging problems, focus on strengthening the following skills:
- Visualization: Being able to visualize the problem, whether it’s through diagrams or mental imagery, helps in understanding how different elements are related.
- Logical Reasoning: Approaching problems step by step, breaking them down into smaller, manageable parts, and using logical progression to reach conclusions.
- Proficiency in Theorems: Familiarity with a variety of theorems and their applications is crucial, as many advanced problems build upon these foundational ideas.
- Practice with Complex Figures: Working with irregular polygons, 3D shapes, and advanced transformations helps to develop the ability to approach any type of problem with confidence.
Effective Strategies for Tackling Difficult Problems
Here are some strategies that can help solve advanced problems more efficiently:
- Break It Down: Start by simplifying the problem. Identify known information and unknowns, and determine what tools or formulas will be useful.
- Work Backwards: In some cases, it may be helpful to start with the solution and reverse-engineer the problem to find the necessary steps.
- Look for Symmetry and Patterns: Advanced problems often involve patterns that can simplify the solution. Look for repeating elements or symmetries that can lead to shortcuts.
- Use Different Approaches: If one method isn’t working, try another approach. For example, use algebraic methods alongside geometric reasoning to find a solution.