My HRW Geometry Answers for Better Understanding

Solving mathematical problems can be a challenging task, especially when concepts seem complex or difficult to grasp. Having a clear and structured approach to these problems is key to overcoming obstacles and improving understanding. With the right guidance, each problem becomes an opportunity to strengthen skills and build confidence.

Effective strategies can make a significant difference in how problems are approached. Whether it’s understanding the fundamentals or tackling more advanced techniques, a well-thought-out method allows for greater clarity and accuracy. By breaking down each step and focusing on the core principles, anyone can improve their problem-solving abilities.

Through consistent practice and by learning from each experience, progress is inevitable. This section will explore various methods to enhance your problem-solving skills, offering practical advice and insights along the way. The aim is to provide you with the tools to succeed and gain a deeper understanding of the subject matter at hand.

Comprehensive Guide to Mathematical Problem Solutions

Solving mathematical challenges requires a methodical approach to ensure accuracy and understanding. A comprehensive guide focuses on providing step-by-step solutions that clarify the most complex topics. By breaking down problems into manageable parts, the process becomes more intuitive and less overwhelming.

Understanding the core concepts is essential for effectively addressing each problem. It involves recognizing patterns, applying appropriate techniques, and practicing consistently. With the right tools and strategies, anyone can enhance their problem-solving skills and build confidence in their mathematical abilities.

Each section of this guide is designed to offer detailed explanations, tips for success, and practical examples. Whether you are tackling basic concepts or more intricate challenges, these solutions will equip you with the knowledge and skills needed to navigate through mathematical tasks successfully.

Understanding Mathematical Homework Assignments

Mathematical homework can often seem overwhelming, especially when new concepts are introduced. However, breaking down each task into smaller, more manageable steps makes it easier to approach. The key is to fully understand the principles behind each problem before diving into the solution process.

Each assignment is designed to help reinforce important skills and build a deeper understanding of the subject. By carefully reviewing the problem, identifying relevant formulas, and applying logical reasoning, one can approach the work with confidence and clarity. Consistent practice is crucial for mastering the material and ensuring long-term success.

In this section, we will explore how to effectively approach assignments, identify common challenges, and offer strategies to make the learning process more efficient. With the right mindset and tools, you can tackle any mathematical task with greater ease and precision.

How to Tackle Mathematical Problems Effectively

Approaching mathematical challenges requires a strategic mindset. Instead of rushing into solving, take time to analyze the problem thoroughly and identify the best approach. By following a clear process, you can simplify even the most complex tasks.

Here are some steps to tackle mathematical problems effectively:

Understand the problem: Read the question carefully to identify what is being asked. Pay attention to details such as given values and unknowns.
Draw diagrams: Visualizing the problem can provide insight into relationships between elements and help guide the solution.
Identify relevant principles: Determine which concepts or formulas are applicable to the problem at hand.
Break it down: Divide the problem into smaller, manageable steps. This will prevent feeling overwhelmed and allow you to focus on one part at a time.
Work systematically: Apply the appropriate techniques, and move through the problem step by step. Keep track of your work to avoid errors.
Review and verify: Once you’ve arrived at a solution, double-check your steps and verify the final answer for accuracy.

By following these steps, you can improve your approach to solving problems and become more confident in your mathematical abilities. Regular practice and thoughtful problem-solving will help you master even the most challenging tasks.

Step-by-Step Approach to Solving Mathematical Questions

When faced with a mathematical problem, a methodical approach can significantly improve your ability to find the solution. Breaking the problem into clear steps allows you to focus on one aspect at a time, making the task feel less overwhelming. A structured approach also ensures that no important details are overlooked, leading to more accurate results.

Understanding the Problem

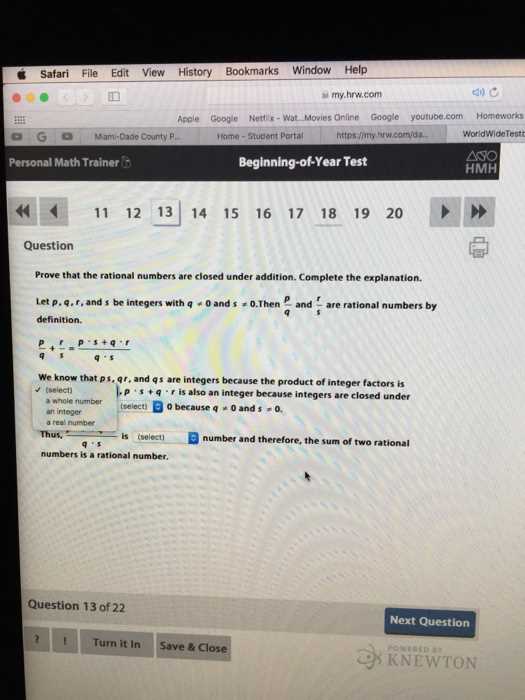
The first step is to carefully read the question and identify what is being asked. Pay attention to key information such as known values, relationships, and the specific goal. If needed, rewrite the problem in your own words to ensure full comprehension.

Solving the Problem

Once you understand the problem, proceed with the following steps:

Visualize the situation: Draw a diagram or model to represent the problem. This will help you see how the different elements are connected and clarify any ambiguities.
Apply relevant formulas: Identify which mathematical principles, theorems, or formulas are applicable to the problem. This will guide your solution process and help you avoid unnecessary calculations.
Work through the steps: Proceed with solving the problem step by step. Carefully apply each formula or technique, keeping track of all intermediate results.
Check your work: After reaching a solution, review each step to ensure no errors were made. Double-check calculations and verify the final result for accuracy.

By following this step-by-step approach, you can approach even the most complex problems with confidence and clarity. Practice will further refine your ability to solve questions efficiently and correctly.

Essential Tips for Mathematical Success

Achieving success in mathematics requires more than just understanding formulas and theorems. It’s about developing effective strategies, maintaining a clear focus, and practicing regularly. By following a set of essential tips, you can enhance your problem-solving abilities and achieve better results.

Focus on Key Concepts

Mastering the core principles is essential to understanding more complex tasks. Focus on the foundational topics and make sure you are comfortable with them before moving on to advanced material. Once you understand the basics, everything else becomes easier to learn and apply.

Practice Regularly

Mathematics is a skill that improves with regular practice. The more problems you solve, the more comfortable and confident you become. Make it a habit to tackle problems daily, even if it’s just for a short period of time.

Work on a variety of problems: Don’t just stick to one type of question. Exploring different problem types helps you understand the material from multiple angles.
Learn from mistakes: When you make an error, take the time to understand why it happened. Analyzing your mistakes helps you avoid them in the future.
Use resources effectively: Take advantage of books, online tutorials, and study groups. These can provide new insights and alternative methods for solving problems.

By incorporating these tips into your study routine, you will develop a deeper understanding of mathematical concepts and improve your ability to tackle any problem confidently.

Common Mathematical Mistakes to Avoid

When solving mathematical problems, it’s easy to fall into common traps that can lead to mistakes. Recognizing these errors early on can help you avoid them and ensure a more accurate approach. In this section, we will highlight some of the most frequent mistakes and provide tips on how to prevent them.

Misinterpreting the Problem

One of the most common mistakes is failing to fully understand what the question is asking. It’s easy to misread a problem, especially when it involves complex wording or multiple steps. Always take the time to carefully read the entire problem and ensure that you understand the task before attempting to solve it.

Overlooking Key Information

Another mistake is neglecting important details such as given values, relationships, or conditions. These elements are crucial for applying the right formulas and methods. Pay attention to all numbers, symbols, and instructions provided in the problem to avoid missing essential information.

Not using the correct formulas: Be sure to apply the appropriate formula for the problem. Using the wrong one can lead to incorrect results.
Skipping steps: Rushing through the solution can cause you to skip critical steps. It’s important to approach each problem methodically and work through every step carefully.
Misapplying theorems or rules: Ensure that you understand the principles you’re using and apply them correctly. Using a theorem in the wrong context is a common mistake that can derail your solution.

By being aware of these common mistakes and taking steps to avoid them, you can improve your problem-solving skills and approach mathematical tasks with greater confidence.

Key Concepts in Mathematics to Master

To truly succeed in solving mathematical problems, it’s essential to have a strong grasp of the fundamental concepts. Mastering these core principles not only makes it easier to solve specific problems but also builds a solid foundation for tackling more advanced topics. In this section, we will highlight some of the most crucial concepts that every student should understand and apply with confidence.

Understanding shapes and their properties is a critical foundation in this field. Recognizing the characteristics of different figures, such as angles, sides, and symmetry, allows you to approach problems more strategically. Knowing the relationships between various shapes helps you to connect the dots and apply the right methods for problem-solving.

Another key concept to master is the ability to calculate areas, volumes, and perimeters. These calculations are frequently used in many problems and understanding the underlying principles can save you time and effort. Equally important is the ability to work with ratios, proportions, and different units of measurement, as they play a significant role in many mathematical tasks.

Angles and their properties: Mastering how to calculate and apply angles is essential for solving many types of problems.
Symmetry and transformations: Recognizing and applying concepts such as reflections, rotations, and translations is important for understanding spatial relationships.
Congruence and similarity: Understanding how shapes can be equal or proportional helps to solve problems involving comparison and equivalence.

By focusing on these key concepts, you will strengthen your problem-solving abilities and build a deeper understanding of the subject. Regular practice with these fundamentals is the key to becoming proficient and confident in tackling a wide range of tasks.

Breaking Down Mathematical Word Problems

Mathematical word problems can often seem overwhelming due to their complexity and the need to extract relevant information from text. However, by approaching them step-by-step, you can simplify the process and make solving these problems more manageable. The key is to carefully interpret the given information and determine what the problem is truly asking for.

Start by reading the problem thoroughly and identifying the key pieces of information. Look for numbers, relationships, and any specific instructions that are given. It’s important to highlight or underline these details to make them easier to reference as you solve the problem.

Next, visualize the situation if possible. Drawing a diagram or creating a chart can help you better understand the problem and identify the connections between different elements. This visual representation often makes it easier to see the solution path.

Identify what’s being asked: Clearly define the goal of the problem. What exactly are you trying to find?
Translate the text into mathematical terms: Convert the relationships described in words into equations or expressions.
Break down the problem into smaller parts: If the problem involves multiple steps, approach each one individually to avoid confusion.
Check your work: After finding a solution, revisit the problem and make sure your answer makes sense in the context of the question.

By following this structured approach, you can improve your ability to tackle mathematical word problems with greater confidence and accuracy.

Using Diagrams to Solve Mathematical Questions

Diagrams are powerful tools that can make complex mathematical problems much easier to understand and solve. By visually representing the given information, diagrams help you see relationships, angles, and proportions that may be difficult to grasp from text alone. Using diagrams allows you to break down problems into more manageable steps and apply the correct methods with greater clarity.

Why Diagrams Are Important

When tackling problems that involve shapes, angles, or spatial relationships, drawing a diagram can make the task simpler and more intuitive. A diagram not only clarifies the situation but also provides a visual reference that you can refer back to while solving the problem. Whether it’s a triangle, a circle, or a complex figure, diagrams help you identify key elements like sides, angles, and distances, allowing for more accurate calculations.

How to Create and Use Diagrams Effectively

Creating a useful diagram involves more than just sketching a random shape. Follow these steps to ensure your diagram is accurate and helpful:

Start with the basics: Draw the shape or figure as accurately as possible, labeling all the known elements such as sides, angles, and any given values.
Mark unknowns clearly: If there are unknown values, label them with variables to make it clear what needs to be calculated.
Highlight important relationships: Use lines or markings to indicate parallel sides, equal angles, or symmetry, as these can help you identify the right formulas and strategies.
Include a key or legend: If necessary, provide a key to explain the symbols or notations used in the diagram.

Here’s an example of a simple diagram to help visualize a geometric problem:

Element	Value
Base of triangle	5 units
Height of triangle	10 units
Area of triangle	25 square units

In this example, the diagram would show a triangle with the labeled base and height, allowing you to easily apply the area formula for triangles. This visualization simplifies the process of solving the problem and ensures that no crucial information is overlooked.

By incorporating diagrams into your problem-solving process, you can increase both your speed and accuracy in tackling a wide range of mathematical questions.

How to Check Your Mathematical Solutions

After working through a mathematical problem, it is crucial to verify the solution to ensure its accuracy. Even if you feel confident in your approach, errors can easily slip through unnoticed. Checking your work involves reviewing each step carefully, ensuring that no detail has been overlooked, and confirming that your solution aligns with the given information.

One effective method to check your solution is to retrace your steps. Start by reviewing the problem statement and confirming that all the given values and conditions have been correctly interpreted. Next, go through each calculation or operation again, making sure that all formulas were applied properly and that no steps were skipped or misunderstood.

Another important tip is to use estimation. If possible, estimate the result before solving the problem. For instance, if you’re calculating an area or distance, quickly estimate what the answer should be based on the problem’s context. After you solve it, compare your answer to your estimation. If the result seems far off, it could indicate an error in your calculations.

Check your units: Ensure that all units are consistent and correct. For example, if you’re working with lengths, make sure all measurements are in the same unit before performing calculations.
Use alternative methods: If applicable, solve the problem using a different method or formula and compare the results. This can serve as a good cross-check.
Review your diagram: If you used a visual representation to solve the problem, revisit it. Make sure it accurately reflects the problem and that all labeled values are correct.

By following these steps, you can increase the likelihood of catching any mistakes and ensure that your solution is correct. Regularly checking your work is a vital part of the learning process and will help you improve your problem-solving skills over time.

Importance of Practice in Mathematical Problem-Solving

Mastering any subject, particularly one that involves complex problem-solving, requires consistent practice. The more you engage with the material, the deeper your understanding becomes. Regularly working through problems helps reinforce concepts, develop critical thinking skills, and improve your ability to tackle a variety of challenges with confidence and accuracy.

When it comes to solving mathematical problems, repetition is key. Each time you solve a problem, you are not only reinforcing the techniques and methods used but also improving your ability to identify patterns and recognize different problem types. This builds a strong foundation that will make future problems easier to approach and solve.

Why Practice is Essential

Here are some reasons why practicing regularly is so important:

Increases familiarity with problem types: By practicing, you become more comfortable with different problem structures and can quickly identify the most efficient solution strategies.
Enhances memory retention: Repeated exposure to the same concepts and techniques helps commit them to memory, making it easier to recall them when needed.
Improves speed and accuracy: As you practice more, your ability to work through problems faster and more accurately improves, which is crucial during timed assessments.
Builds confidence: The more problems you solve, the more confident you become in your ability to handle new and unfamiliar challenges.

Tips for Effective Practice

To make your practice sessions as effective as possible, try incorporating the following strategies:

Start with simpler problems: Build your confidence by solving easier problems before gradually moving on to more difficult ones.
Track your progress: Keep a record of your practice problems and solutions. Reviewing your mistakes can help you identify areas where you need more work.
Practice regularly: Set aside time each day or week to practice solving problems. Consistent practice is more beneficial than cramming.
Vary the problem types: Work on a mix of problems to ensure you develop a well-rounded skill set. Don’t just focus on one topic or type of question.

With dedication and consistent practice, you will not only improve your problem-solving skills but also develop a deeper understanding of mathematical principles, leading to greater success in tackling more complex challenges.

How to Improve Your Mathematical Skills

Enhancing your problem-solving abilities requires a combination of understanding key concepts, practicing regularly, and developing efficient strategies. Whether you’re trying to master new techniques or improve your speed and accuracy, there are several approaches you can take to sharpen your skills. The key is consistent effort and the willingness to learn from mistakes.

Improving your mathematical skills is not just about memorizing formulas; it’s about building a deeper understanding of the logic behind the solutions. By breaking down problems, recognizing patterns, and working through various types of exercises, you can develop the necessary tools to tackle complex challenges with ease.

Strategies to Improve Your Skills

Here are some practical steps to help you improve your problem-solving abilities:

Practice regularly: Consistency is crucial. Set aside time each day to solve problems. The more you practice, the more comfortable you will become with various techniques and problem types.
Focus on understanding concepts: Rather than just memorizing formulas, strive to understand the reasoning behind them. When you grasp the “why” behind a technique, it becomes easier to apply it to different problems.
Work through a variety of problems: Expose yourself to different problem types to strengthen your skills. Working on a range of exercises will help you develop a versatile approach to problem-solving.
Review mistakes: After solving a problem, take time to check your work. If you made a mistake, analyze it to understand why it happened. This reflection will help you avoid similar errors in the future.
Use visual aids: Diagrams, charts, and drawings can help make complex problems more tangible. Drawing a clear picture of the problem can often lead to a simpler solution.

Developing Stronger Problem-Solving Habits

In addition to practicing regularly, adopting effective problem-solving habits can significantly boost your performance:

Break down complex problems: If you encounter a difficult problem, break it into smaller, more manageable steps. This approach makes the problem seem less overwhelming and helps you focus on one part at a time.
Stay patient and persistent: Don’t rush through problems. Take your time to understand the question fully and consider multiple approaches before solving.
Seek help when needed: If you’re struggling with a particular concept or technique, don’t hesitate to ask for guidance. Teachers, tutors, or study groups can offer valuable insights and explanations.

Improving your mathematical skills is a gradual process that requires practice, patience, and dedication. By following these strategies and maintaining a positive, proactive attitude, you’ll find that you become more confident in your problem-solving abilities and more prepared to tackle new challenges.

Formulas You Need to Know

Understanding essential mathematical formulas is crucial for solving problems efficiently. These key equations provide the foundation for tackling a wide range of challenges, from calculating areas to solving complex relationships between different shapes. Familiarizing yourself with these formulas not only helps streamline problem-solving but also enhances your overall mathematical comprehension.

By mastering the most commonly used formulas, you gain the ability to approach problems with confidence and clarity. Whether you’re working on basic calculations or more advanced exercises, knowing the right formula to apply at the right time can make all the difference.

Basic Area Formulas

Here are some fundamental formulas for calculating the areas of various shapes:

Rectangle: Area = length × width
Square: Area = side × side
Triangle: Area = 1/2 × base × height
Circle: Area = π × radius²

Perimeter and Volume Formulas

In addition to area calculations, here are some key formulas for perimeter and volume:

Rectangle: Perimeter = 2 × (length + width)
Square: Perimeter = 4 × side
Circle: Circumference = 2 × π × radius
Cube: Volume = side³
Rectangular Prism: Volume = length × width × height

These formulas serve as the building blocks for many problems and should be thoroughly understood and practiced. As you become more familiar with these equations, applying them to various scenarios will become quicker and easier.

Understanding Proofs in Mathematics

Proofs are a fundamental part of mathematical reasoning. They provide the logical foundation for establishing the validity of statements or concepts. By using a combination of axioms, theorems, and logical deductions, proofs help us demonstrate why something is true, rather than just assuming it. Mastering the art of constructing and understanding proofs is essential for progressing in various mathematical fields.

There are different types of proofs, each with its own approach and style. Whether you’re proving a simple identity or a complex geometric relationship, the process generally involves a series of logical steps that lead to a final conclusion. Developing proof-writing skills requires practice and a deep understanding of both the principles and the relationships between mathematical elements.

Types of Proofs

There are several common methods of proving mathematical statements. Some of the most important types include:

Direct Proof: This is the most straightforward method, where you start from known facts and apply logical steps to reach the desired conclusion.
Indirect Proof (Proof by Contradiction): In this method, you assume the opposite of what you want to prove and show that it leads to a contradiction.
Proof by Induction: This technique is often used for proving statements about sequences or patterns. It involves proving a base case and then showing that if the statement holds for one case, it will hold for the next.
Proof by Construction: Here, you prove a statement by explicitly constructing an example that satisfies the conditions of the problem.

Steps in a Proof

To effectively construct a proof, certain steps are often followed. These may vary depending on the type of proof, but generally include the following:

Understand the Problem: Carefully read and comprehend the given information and what needs to be proven.
Gather Known Facts: Identify relevant theorems, definitions, and previously proven results that will be used in the proof.
Choose the Proof Method: Decide on the most appropriate method based on the nature of the statement being proven.
Logical Deductions: Make logical connections between the facts and proceed step by step toward the conclusion.
Conclude the Proof: Conclude the proof by clearly stating the result and ensuring every logical step is justified.

While constructing proofs may seem challenging at first, with practice, the process becomes more intuitive. By mastering the logical structure and different methods of proof, you’ll develop a deeper understanding of mathematics and improve your ability to reason critically.

How to Stay Organized in Mathematics

Staying organized is key to mastering any subject, especially when it involves complex concepts and problem-solving. In mathematical studies, maintaining an orderly approach can significantly improve your ability to understand, retain, and apply new information. Whether you’re working on solving problems, reviewing concepts, or preparing for exams, having a clear and structured system will save you time and reduce stress.

To stay organized, it’s essential to develop habits that help you manage your notes, track your progress, and ensure you’re using the right resources at the right time. This approach will also allow you to easily locate important information and identify areas where you need more practice.

Key Tips for Staying Organized

Here are some helpful strategies to help you stay organized in your studies:

Maintain a Dedicated Notebook: Keep a single notebook or binder specifically for mathematical work. Use it to jot down important definitions, theorems, and examples. This allows you to have all your notes in one place for easy reference.
Use Color-Coding: Color-code your notes, formulas, and key concepts. This helps visually separate different topics and makes it easier to locate specific information when reviewing.
Make Detailed Problem Sets: Break down problems into smaller steps and write each step clearly. This helps you stay focused and ensures you understand the process of solving each type of problem.
Review Regularly: Set aside time to review and organize your work weekly. This keeps concepts fresh and allows you to track your progress over time.
Use a Study Planner: Plan your study sessions and set specific goals. A study planner ensures that you allocate sufficient time to each topic and stay on track.

Organizing Your Resources

In addition to keeping your notes well-organized, managing your study materials is equally important. Having an organized approach to resources like textbooks, online materials, and practice sets will help you stay focused on your learning goals.

Resource	Organization Method
Textbook	Use sticky notes or bookmarks to mark key chapters, definitions, and examples.
Online Materials	Create a digital folder for saved articles, practice problems, and videos for easy access.
Practice Problems	Label problem sets by type (e.g., equations, proofs, calculations) and organize them by difficulty.

By applying these organization techniques, you can improve your overall efficiency and feel more confident in your ability to approach and solve problems in mathematics.

Mastering Mathematical Concepts with Online Resources

In today’s digital age, online resources have become an essential tool for mastering complex subjects. When it comes to mastering mathematical concepts, the internet offers a wealth of materials to enhance your understanding and support your learning. From video tutorials to interactive quizzes, the variety of available tools makes it easier than ever to access valuable educational content that can help clarify difficult topics and reinforce learning.

By utilizing these online tools, you can take control of your learning pace, revisit challenging topics, and test your knowledge in real-time. Whether you’re seeking visual aids, step-by-step explanations, or additional practice problems, the right online resources can make all the difference in gaining confidence and improving your skills.

Key Online Resources to Explore

Here are some of the most effective online tools that can help you improve your understanding of mathematical concepts:

Interactive Learning Platforms: Websites like Khan Academy, Coursera, or edX offer free courses and tutorials on various math topics. These platforms often include practice exercises and video lessons that allow you to learn at your own pace.
YouTube Tutorials: YouTube is home to numerous educators and math enthusiasts who provide easy-to-follow video tutorials. Channels like PatrickJMT, Professor Leonard, and 3Blue1Brown offer in-depth explanations and visual demonstrations of key concepts.
Online Math Solvers: Tools like WolframAlpha and Symbolab can help you solve specific problems step by step. These platforms also provide explanations for each step, making them great for understanding complex problem-solving methods.
Practice Problem Websites: Websites such as Brilliant.org and Mathway provide a wide range of practice problems and puzzles. These platforms allow you to test your skills and receive instant feedback on your answers.
Math Forums and Communities: Engaging with online communities such as Stack Exchange or Reddit’s MathHelp subreddit can be a great way to ask questions and learn from others. These communities often feature experienced mathematicians who can offer valuable advice and solutions.

How to Maximize Online Learning

To make the most of online learning resources, consider the following tips:

Set Clear Goals: Determine which areas of mathematics you want to focus on and prioritize resources that align with your goals.
Practice Consistently: Regular practice is key to mastering any concept. Use online quizzes and problem sets to reinforce your learning.
Engage with the Community: Don’t hesitate to participate in forums or comment sections to ask questions and clarify doubts.
Review and Repeat: Revisit challenging concepts until they feel more intuitive. Online resources allow you to go back and review content as often as needed.

Resource	Key Feature	Best For
Khan Academy	Video lessons and interactive exercises	Fundamentals and beginner topics
WolframAlpha	Problem-solving and step-by-step solutions	Calculations and explanations
Brilliant.org	Interactive puzzles and learning challenges	Advanced practice and problem-solving
YouTube	Video tutorials and visual explanations	Understanding complex concepts visually

By combining these online resources with your own practice and commitment, you can significantly improve your understanding of mathematical topics and develop the problem-solving skills needed to succeed.

How Mathematical Skills Apply in Real Life

The ability to understand shapes, sizes, and spatial relationships is essential in many areas of daily life. Whether it’s designing a home, calculating distances, or understanding how things fit together, these concepts are all rooted in mathematical principles. Learning how to apply these principles effectively allows us to solve practical problems, make informed decisions, and improve the way we interact with the world around us.

From architecture to technology, the skills developed through mathematical study have wide-reaching applications. The logical thinking, problem-solving, and spatial awareness fostered by mathematical education are not only useful in academic settings but are also crucial in everyday tasks and in many professional fields.

Here are just a few examples of how mathematical skills can be applied in real-world scenarios:

Construction and Design: Architects and engineers use these skills to create blueprints, calculate structural integrity, and design functional spaces. Whether it’s the angles of a roof, the measurements of a room, or the layout of a building, these professionals rely on advanced mathematical principles.
Technology and Coding: Software developers and computer engineers apply these skills to create algorithms, manage data, and build user interfaces. Spatial reasoning also plays a role in virtual reality, 3D modeling, and game design.
Navigation and Travel: Pilots, drivers, and sailors use mathematical concepts to navigate from one place to another. Understanding distances, estimating travel time, and calculating fuel usage are all tasks that involve basic math principles.
Art and Design: Artists, graphic designers, and interior decorators use measurements, symmetry, and proportion to create aesthetically pleasing compositions and functional designs. Geometry plays a central role in creating everything from paintings to websites.
Financial Planning: From budgeting to investing, these skills are crucial for understanding financial trends, calculating interest rates, and managing personal and business finances. Investment analysts and accountants use these principles to evaluate opportunities and make data-driven decisions.

By recognizing the role of mathematics in real life, students and professionals alike can gain a deeper appreciation for the relevance of these skills, seeing them not only as academic exercises but as tools to solve practical, real-world challenges.

Staying Motivated While Studying Mathematical Concepts

Maintaining focus and enthusiasm while learning complex topics can be challenging. Whether you’re tackling new theories, solving intricate problems, or preparing for exams, staying motivated is essential for progress. It’s easy to feel overwhelmed, but understanding how to stay motivated can turn your study sessions into productive and rewarding experiences.

One of the key strategies for keeping motivation high is setting clear, achievable goals. Breaking down larger concepts into smaller, manageable tasks makes it easier to track progress and see immediate results. This not only boosts confidence but also makes studying feel less daunting.

Another important aspect is connecting the material to real-world applications. When you understand how the concepts you’re learning can be used in everyday life or future careers, it becomes easier to stay engaged. Whether you’re learning about measurements in construction or calculations in technology, knowing the practical relevance of the material can make a significant difference in your motivation.

Set Short-Term Goals: Focus on mastering small chunks of content at a time, rather than trying to grasp everything at once.
Find the Real-World Applications: Explore how the concepts you study are used in fields like architecture, design, and even finance.
Take Regular Breaks: Short breaks between study sessions can help you stay refreshed and maintain focus over a longer period.
Reward Yourself: Celebrate small victories, like completing a difficult problem or mastering a concept, with a treat or a break.
Stay Positive: Cultivate a positive mindset by focusing on progress, not perfection. Remind yourself that challenges are opportunities to improve.

Finally, remember that motivation doesn’t always come naturally. It requires effort, planning, and sometimes, a little self-discipline. By using these strategies, you can stay motivated and make your study time more efficient and enjoyable.