Understanding the relationship between various geometric shapes and their representations is crucial for mastering mathematical challenges. In this section, we will delve into the core principles behind solving complex problems related to circular forms and their properties. Whether you are trying to simplify the process or reinforce your knowledge, this content provides the essential tools for effective learning.
By focusing on key concepts such as the general form and transformations, we will explore how to approach these problems with confidence. With a combination of practical tips and theoretical insight, you’ll be equipped to tackle a wide range of related tasks. This approach is designed to ensure clarity and enhance your problem-solving abilities, whether in academic settings or everyday applications.
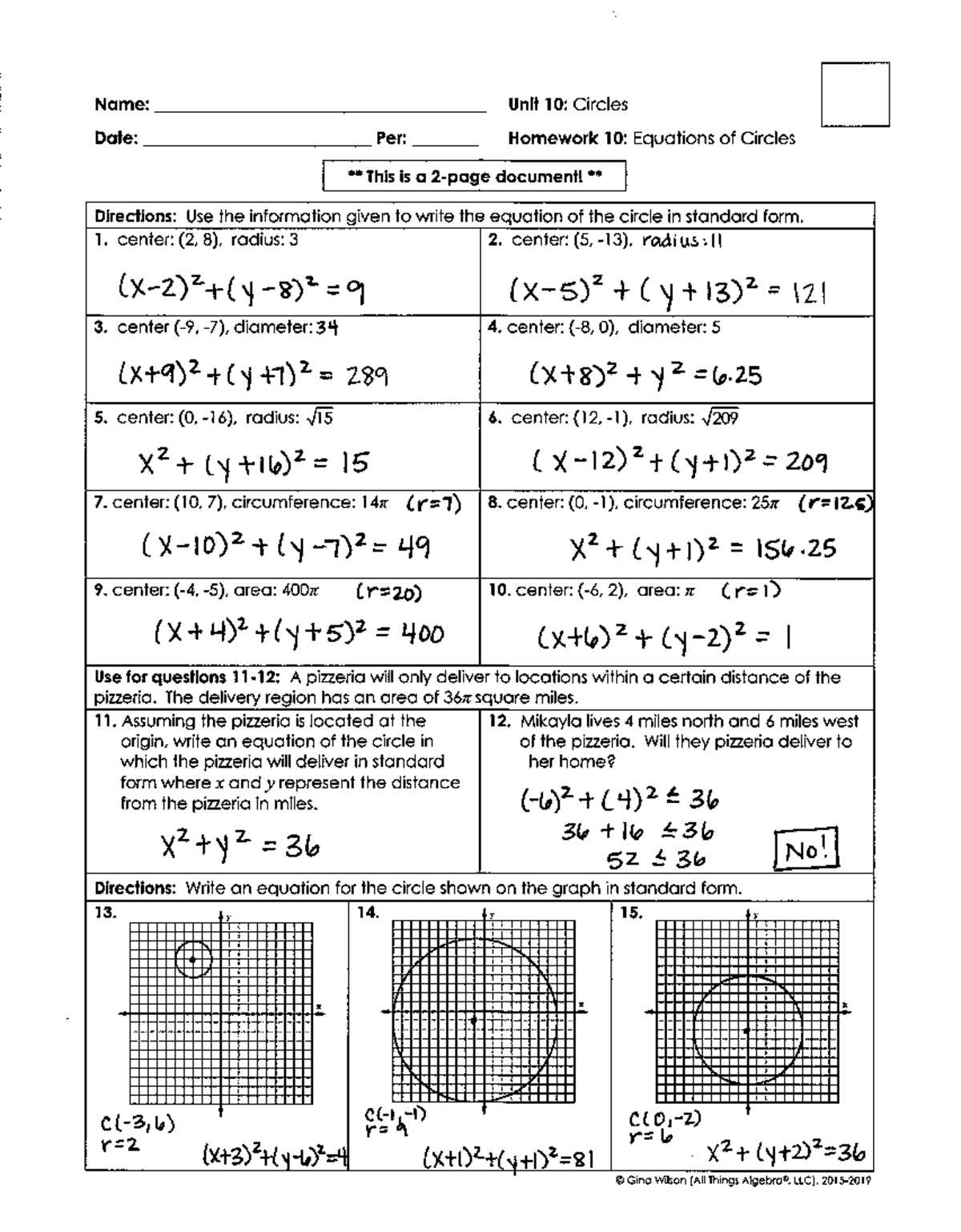
10-8 Study Guide and Intervention Equations of Circles Answers
In this section, we will focus on understanding key mathematical problems related to circular figures. The main goal is to guide learners through solving these challenges step by step, ensuring a solid grasp of the underlying concepts. By working through a variety of examples, you will gain the skills needed to approach similar tasks with ease and confidence.
As we break down the steps involved, particular attention will be given to transforming complex forms into simpler, more manageable versions. This approach will help you not only solve problems but also understand the logic behind each calculation. Below, we present a table summarizing common techniques and their applications in various scenarios:
| Method | Description | Application |
|---|---|---|
| Standard Form | Transforming a general equation into a simplified form | Helps in identifying key properties like radius and center |
| Graphing | Plotting the problem on a coordinate plane for better visualization | Useful for understanding the geometric relationships and verifying solutions |
| Distance Formula | Calculating the distance between points based on given coordinates | Crucial for determining the radius and center of the figure |
| Factoring | Breaking down equations to find key values and simplify the expression | Effective for solving complex problems by simplifying the algebra |
By applying these techniques, you will be able to simplify your approach to these mathematical challenges and develop a deeper understanding of circular geometry. With practice, these methods will become second nature, allowing you to solve related problems with precision and efficiency.
Understanding Circle Equation Basics
Grasping the foundational principles behind the mathematical representation of round shapes is essential for solving related problems. By familiarizing yourself with the core concepts, such as the relationship between various components like radius and center, you’ll be able to approach problems more efficiently. This section covers the fundamental ideas that are key to understanding how these forms are represented algebraically and geometrically.
The core of this topic lies in recognizing how the values within an equation relate to the physical properties of the shape. By mastering the manipulation of these representations, learners can develop a clearer understanding of how to derive solutions and visualize the results. This knowledge forms the foundation for tackling more complex problems in geometry and beyond.
Key Concepts in Circle Geometry
Understanding the essential principles of geometric figures is crucial for solving related mathematical problems. This section will introduce key concepts that form the basis of working with round shapes, helping you build a strong foundation in this area. By mastering these core ideas, you’ll be better equipped to approach more complex challenges with confidence.
The most important concepts involve the relationship between the center, radius, and various points on the shape. Knowing how to interpret these relationships algebraically and geometrically is fundamental. Additionally, understanding how to work with different forms of representation, whether in equations or diagrams, will significantly enhance your ability to analyze and solve problems efficiently.
Solving Circle Equations Step by Step
Approaching problems related to round shapes can seem challenging at first, but breaking them down into manageable steps can make the process much easier. This section will guide you through the process of solving such problems methodically, ensuring that you understand each phase clearly before moving on to the next. By following these steps, you’ll be able to solve these problems with confidence and accuracy.
Here’s a simple step-by-step process for tackling these problems:
- Identify the Key Components: Recognize the values for the center and radius, and understand how they relate to the given form.
- Rewrite the Problem in Standard Form: If necessary, transform the equation into a more familiar structure that highlights the important components.
- Use the Pythagorean Theorem: If working with distances or coordinates, apply the theorem to find relationships between points on the figure.
- Simplify the Expression: Combine like terms and perform algebraic operations to simplify the equation, making it easier to interpret.
- Graph the Result: Plot the equation on a coordinate plane to visualize the geometric relationships and check for accuracy.
By following these structured steps, you’ll be able to tackle problems involving round shapes more effectively and accurately. With practice, these steps will become second nature, allowing you to solve related tasks quickly and efficiently.
Importance of Standard Form of Equations
The standard form of mathematical representations plays a critical role in simplifying and solving problems involving round shapes. It provides a clear and structured way to understand the relationship between key elements, such as the center and radius. By expressing the equation in this form, the core components become easier to identify and work with, ensuring greater accuracy in calculations and a better understanding of the underlying geometry.
When the equation is written in standard form, it allows for quicker analysis and comparison between different problems. This format also facilitates the process of graphing, as it clearly outlines the critical values needed to plot the shape accurately on a coordinate plane. In addition, working with a consistent structure minimizes errors and enhances the overall efficiency of solving these types of problems.
Identifying Circle Components in Equations
Understanding the key elements within a mathematical representation of a round shape is essential for solving related problems. Each component of the expression corresponds to a specific geometric feature, such as the center or the radius. Recognizing these components quickly allows for a more efficient approach to solving and interpreting the problem.
In most cases, the equation is structured in a way that the values for the center and radius can be easily extracted. The center is typically represented by a pair of numbers, while the radius is indicated by a value that defines the size of the shape. By identifying these parts, you gain a clearer understanding of the geometric properties and can move forward with the solution more confidently.
Common Mistakes in Circle Equations
When working with geometric representations, it’s easy to make errors that can lead to incorrect solutions. Understanding these common mistakes is crucial for avoiding pitfalls and improving your problem-solving skills. In this section, we will highlight some of the most frequent errors people make when handling these types of problems and offer tips on how to avoid them.
Common Errors in Formulating the Problem

- Incorrectly identifying the center and radius values.
- Forgetting to square the radius when working with certain forms.
- Misplacing terms or signs in the equation, leading to wrong results.
- Not converting equations to standard form before solving.
Common Graphing Mistakes
- Plotting the center at the wrong coordinates.
- Incorrectly determining the size of the shape by misinterpreting the radius.
- Not checking the symmetry of the figure after graphing.
- Overlooking negative values for radius or center coordinates.
By being aware of these typical mistakes, you can work more effectively and minimize errors in your calculations. Regular practice and careful attention to detail will help you avoid these issues and become more proficient in solving these types of problems.
Using the Distance Formula for Circles
The distance formula is a powerful tool for calculating the distance between two points in a plane. In the context of geometric shapes, it plays an important role in determining the relationship between the center and any point on the figure. By applying this formula, you can find distances that help define the properties of the shape, such as its radius or distance from a specific point.
To calculate the distance between two points, use the formula:
d = √((x2 – x1)² + (y2 – y1)²)
Here, (x1, y1) and (x2, y2) are the coordinates of the two points, and d represents the distance between them. This formula is especially useful when working with problems that involve determining the radius or checking if a point lies on the shape.
Below is a table outlining how the distance formula can be applied to different problems:
| Scenario | Formula Application | Outcome |
|---|---|---|
| Finding the radius | Apply the formula between the center and a point on the boundary | Determines the radius of the shape |
| Checking if a point lies on the figure | Calculate the distance from the point to the center | If the distance equals the radius, the point lies on the figure |
| Measuring the distance between two points | Use the formula between any two points | Gives the straight-line distance between the points |
By using the distance formula in various scenarios, you can gain a deeper understanding of how points relate to geometric figures. It is a valuable tool for solving many problems that require determining distances or verifying properties of shapes.
Transforming General Form to Standard Form
Converting a general mathematical expression into a structured, recognizable format is an important step in solving related problems. By transforming the general form into a more manageable structure, it becomes easier to identify key elements, such as the center and radius, which are essential for understanding the geometric properties of the figure. This process is not only useful for graphing but also for analyzing the figure’s characteristics in greater detail.
The transformation process typically involves completing the square for both variables and then rearranging terms to achieve the desired structure. Below is a breakdown of the general process and an example to help illustrate the steps:
| Step | Action | Explanation |
|---|---|---|
| 1 | Group the terms involving x and y | Start by grouping the variables that contain x and y separately on each side of the equation. |
| 2 | Complete the square for both x and y terms | Add the necessary values to complete the square, ensuring both sides of the equation are balanced. |
| 3 | Rewrite the equation in standard form | After completing the square, simplify the expression into the standard form of the equation. |
By following these steps, you can easily convert any general form into the standard representation, making it simpler to work with and understand. This transformation is crucial for solving problems that require specific geometric properties, such as finding the radius or center of the figure.
Applications of Circle Equations in Real Life
The principles of geometry are not limited to the classroom; they are used extensively in many practical fields. One of the key concepts is understanding how to represent shapes mathematically. In various real-world situations, this knowledge helps in designing, analyzing, and solving problems related to round shapes, whether in construction, technology, or other industries. By applying mathematical representations, professionals can solve complex problems more effectively and efficiently.
For instance, in engineering, architects often use these mathematical models to design circular structures, such as domes or arches. In transportation, the calculation of turns and curves in roads or railways often involves the use of similar models to ensure safe and smooth transitions. Additionally, in astronomy, the paths of planets and moons can be described using circular models, helping scientists predict orbits and trajectories.
Here are some common real-life applications:
- Designing Circular Structures: Engineers use these models to calculate stress points, material strength, and durability in structures like bridges, tunnels, and domes.
- Navigation and Mapping: GPS systems rely on spherical coordinates and circular geometry to calculate distances and directions accurately.
- Optics: In lens manufacturing, understanding how light reflects and refracts through curved surfaces is essential for creating optical devices.
- Sports: The design of tracks, fields, and even equipment like basketball hoops and soccer goals involves geometric principles based on circular shapes.
Understanding how to work with circular models in these contexts makes it possible to solve real-world problems, optimize designs, and predict outcomes more precisely. With further study and application, the potential for using circular geometry in practical scenarios is limitless.
Solving Word Problems Involving Circles
Word problems are a common way to apply mathematical concepts in practical scenarios. When dealing with round shapes, these problems often require converting real-life situations into mathematical models. By understanding the relationships between various components, such as the center, radius, and perimeter, it’s possible to translate a word problem into a solvable equation. This process involves careful analysis and sometimes multiple steps to find the solution.
The key to solving these types of problems is recognizing the underlying structure of the situation and applying the correct formulas. For example, in problems involving the area of a circular garden or the circumference of a wheel, you can use well-established mathematical expressions to find the unknowns. Identifying the known values and understanding what the problem asks for are crucial steps in the solution process.
Here are some general steps for solving word problems related to round shapes:
- Identify the Known Values: Determine the given information, such as the radius, diameter, or other dimensions mentioned in the problem.
- Choose the Correct Formula: Depending on the problem, you may need to use formulas for area, perimeter, or other related measurements. These are often based on the radius or diameter.
- Substitute Values: Plug the known values into the appropriate formula and simplify the equation as needed.
- Solve for the Unknown: Perform the necessary calculations to find the unknown quantity, whether it’s the area, circumference, or another measurement.
By following these steps, you can approach word problems involving circular shapes systematically, ensuring accuracy in your calculations. Practicing with different scenarios will also help build a stronger intuition for applying mathematical principles to solve everyday problems.
Circle Equation Problems with Multiple Variables
When dealing with problems involving round shapes, it’s common to encounter scenarios where more than one variable is involved. These types of problems often require you to solve for multiple unknowns, which can be challenging without a clear understanding of how the variables interact with each other. Typically, these problems will present relationships between the radius, center, and sometimes other characteristics of the shape, requiring you to use algebraic techniques to find the solution.
One of the key steps in solving these problems is identifying how each variable contributes to the overall structure of the situation. For instance, you may need to find the center of a circle given two points that lie on its edge, or you may be asked to determine both the radius and the center using a combination of known values. Understanding how to manipulate multiple variables simultaneously is crucial for solving these more complex problems.
Solving Systems of Equations
In many cases, you will need to use systems of equations to solve for multiple unknowns. For example, if you are given the general form of a shape’s description, you might have two equations that describe different properties of the shape. Solving these simultaneously allows you to isolate the unknowns and find the values that satisfy both conditions.
Using Substitution and Elimination
When tackling these problems, methods like substitution or elimination can be particularly useful. By substituting known values into one equation, you can reduce the number of variables, making it easier to solve for the unknowns. Similarly, the elimination method involves combining equations to cancel out one variable, simplifying the process.
These types of problems can be more challenging but offer a deeper insight into how different elements of geometry and algebra intersect. By mastering these techniques, you’ll be able to solve a wide range of complex problems involving multiple unknowns related to circular shapes.
Strategies for Improving Circle Equation Skills
Mastering the mathematical techniques for solving problems related to round shapes requires both practice and a solid understanding of the core principles. As with any complex subject, refining your skills involves breaking down the process into manageable steps and reinforcing the foundation of key concepts. Whether you’re solving for the radius, center, or other properties, having a structured approach will make tackling these problems easier and more efficient.
One of the most effective ways to improve your abilities is through consistent practice. Working on a variety of problems with different levels of difficulty helps build both confidence and competence. As you solve more problems, you’ll become familiar with common patterns and techniques, making it easier to recognize the appropriate methods for each situation.
Break Down the Problem Step by Step
It’s essential to take a systematic approach to each problem. Start by carefully identifying what is given and what needs to be determined. This can help you organize your thoughts and decide which techniques or formulas to apply. Breaking down each problem into smaller parts allows you to avoid feeling overwhelmed, especially when dealing with more complex situations involving multiple variables.
Review Fundamental Concepts Regularly
Having a strong grasp of the foundational concepts is crucial for solving any mathematical problem. Spend time reviewing key principles related to geometry and algebra that pertain to round shapes. Understanding the relationship between the radius, diameter, and center, as well as recognizing the differences between various forms, will give you the tools you need to solve more complicated problems with ease.
Incorporating these strategies into your study routine will not only help you improve your skills but will also give you a deeper understanding of the subject. With patience and practice, you’ll be able to tackle a wide variety of challenges involving round shapes more effectively.
How to Check Your Circle Equation Answers
Verifying the correctness of your solutions is a crucial step in mastering mathematical problems related to round shapes. Double-checking your results not only ensures accuracy but also helps reinforce the methods and principles you’ve applied. Following a structured approach to reviewing your work can prevent common mistakes and help you build confidence in your problem-solving abilities.
There are several techniques you can use to confirm your results, ranging from simple calculations to visual verification. Each method provides a different way to check the validity of your solution, ensuring that your answers are correct and consistent with the given information.
Review the Given Information
Start by carefully reading the problem again to make sure you’ve interpreted the given data correctly. Confirm the values for the center, radius, and any other parameters that were provided. This will help ensure that you’re working with accurate values throughout the problem.
Substitute Values Back into the Formula
One of the most reliable methods to verify your solution is to substitute the values you obtained into the original formula. Check that the equation holds true by recalculating both sides of the expression. If both sides match, your answer is likely correct.
Graphical Verification
If possible, try plotting the values on a graph to visually confirm that they make sense. For example, if you have the center and radius, you can sketch the circle on a coordinate plane to check whether the solution accurately represents the expected geometric shape. This can be a helpful way to spot any discrepancies in your calculations.
Cross-Check with Another Method
If you’ve solved the problem using one method, consider trying another approach to see if you arrive at the same result. Using different formulas or alternative techniques can help you confirm the accuracy of your solution from multiple perspectives.
By following these strategies, you can confidently verify your solutions and avoid common errors. Regular practice of these verification methods will also improve your overall problem-solving skills, making it easier to tackle more complex challenges in the future.
Advanced Circle Equation Techniques
Mastering complex problems involving round shapes requires a deeper understanding of various methods and strategies. By expanding your knowledge of advanced techniques, you can efficiently solve more challenging problems that go beyond the basics. These approaches allow you to tackle scenarios that require more than just standard formulas, giving you the tools to approach problems from different angles.
In this section, we will explore advanced strategies that go beyond the standard approaches, offering new insights into how to handle more intricate problems involving geometric shapes that fit specific patterns. Understanding these methods will help you excel in solving a variety of higher-level tasks.
Completing the Square for Standard Form Conversion
One of the more advanced techniques involves converting a general form expression into the standard representation using the method of completing the square. This technique is particularly useful when the equation involves multiple variables. By rearranging terms and factoring appropriately, you can transform an equation into a recognizable form that highlights the center and radius of the figure.
- First, group the terms involving x and y together, isolating the constants on the other side.
- Then, complete the square for each variable by adding the appropriate constants inside the groups.
- Finally, rewrite the equation in its standard form, revealing the key parameters.
Using Parametric Equations
Another advanced method for analyzing geometric shapes is through the use of parametric equations. Parametric equations express the coordinates of a point on a round figure in terms of a variable, often denoted as t. By using parametric equations, you can describe the motion or position of points on the shape with greater precision.
- The general form of parametric equations for a round shape is:
- x(t) = h + r * cos(t)
- y(t) = k + r * sin(t)
- Here, (h, k) represents the center, and r is the radius, while t is a parameter that varies.
Using Polar Coordinates
Polar coordinates are another advanced approach that can provide a different perspective on solving problems involving round shapes. Instead of using the traditional Cartesian coordinate system, polar coordinates define a point based on its distance from the origin and the angle from a reference axis. This technique is particularly effective when working with circular figures that are symmetric around the origin.
- The general equation in polar form is:
- r = constant
- This represents a circle with a fixed radius and the origin as its center.
By incorporating these advanced techniques, you can broaden your problem-solving abilities and approach circular geometry from various perspectives. These methods provide more flexibility and efficiency in dealing with complex scenarios that require a deeper understanding of geometry and algebraic manipulation.