
In this section, you’ll explore essential principles that are crucial for mastering foundational mathematical concepts. With a focus on equations, functions, and graphing, the material presents an opportunity to deepen your understanding of core topics and build strong problem-solving skills.
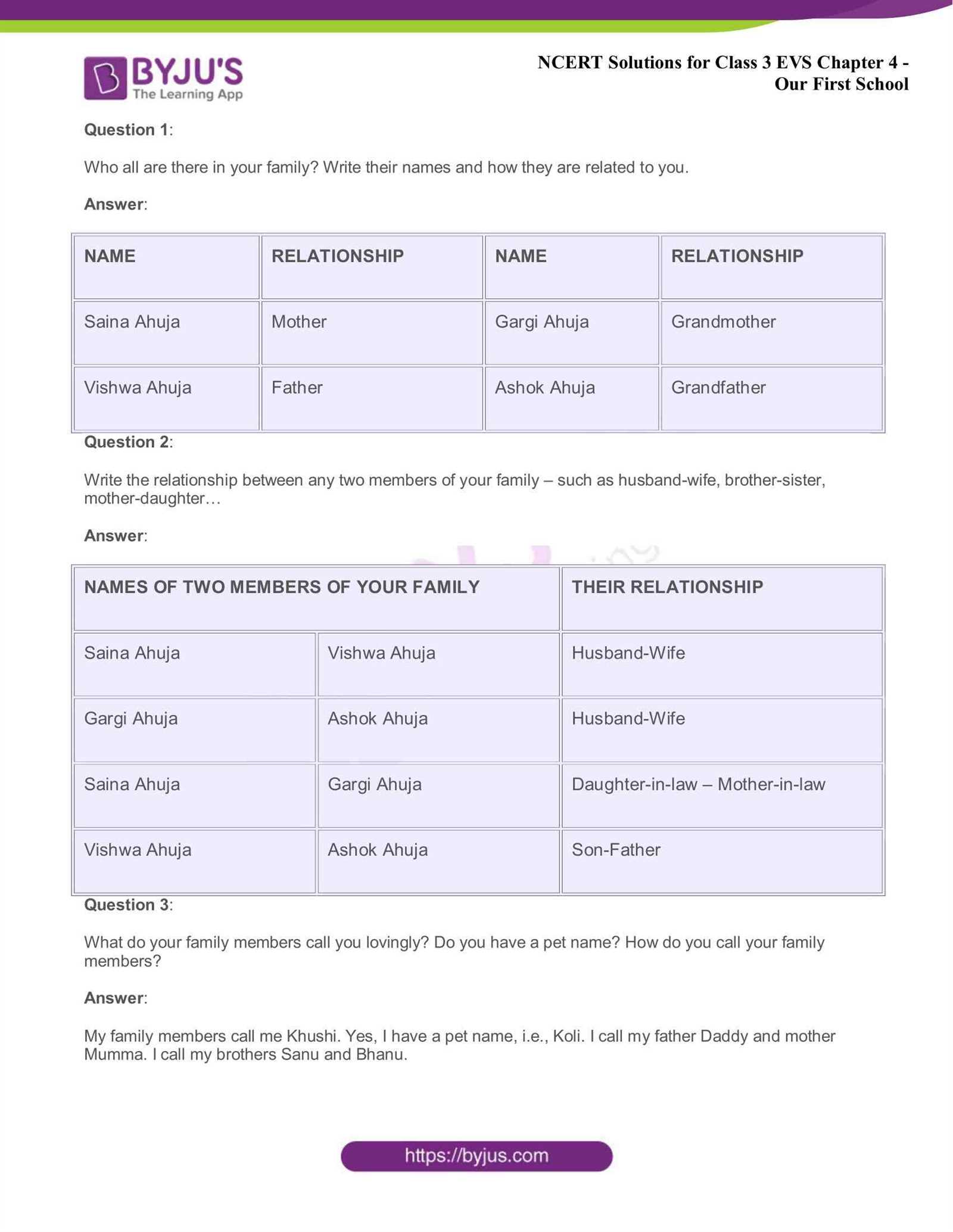
Each concept is explained clearly, ensuring that students can grasp the fundamental techniques needed to approach complex exercises. By practicing various types of problems, you’ll gain the confidence to tackle both basic and advanced challenges with ease. Whether it’s simplifying expressions or solving for unknown variables, this content provides the support necessary to excel.
As you progress through these sections, you’ll find that regular practice with step-by-step explanations will reinforce your ability to apply these methods in different scenarios. Mastering these skills is key to advancing in mathematics and building a solid foundation for future learning.
Algebra 1 Chapter 4 Overview
This section focuses on core concepts that form the foundation of solving equations, understanding relationships between variables, and working with various mathematical expressions. It emphasizes developing problem-solving skills and applying systematic approaches to a variety of exercises. Key topics explored include:
- Understanding linear functions and their graphs
- Solving for unknowns using various methods
- Interpreting equations in real-world scenarios
- Working with inequalities and their graphical representations
- Manipulating expressions through factoring and simplifying
Throughout this section, the focus will be on strengthening your ability to analyze and approach different types of problems. Each concept builds on previous lessons, reinforcing essential techniques that will be useful in more complex studies. By mastering these areas, you will gain the tools necessary for success in more advanced topics.
The exercises and examples provided allow you to apply what you’ve learned, offering practical experience that will improve your overall mathematical proficiency. This overview lays the groundwork for a deeper understanding and provides the tools to solve increasingly challenging problems.
Key Concepts of Algebra 1 Chapter 4
This section highlights the essential ideas that are foundational for solving problems involving equations, functions, and graphing. It covers the core principles that will help you understand how to manipulate expressions and interpret mathematical relationships. The main concepts explored include:
- Understanding linear functions and their graphs
- Identifying and solving equations with variables
- Interpreting real-world scenarios through mathematical models
- Analyzing inequalities and their graphical representations
- Factoring expressions and simplifying complex equations
Grasping these core principles is crucial for building a strong mathematical foundation. By mastering these techniques, you’ll be able to approach various types of problems with confidence and precision. Each concept supports the development of essential skills necessary for solving more advanced challenges in mathematics.
Important Equations to Know

Understanding key formulas is essential for solving problems effectively. These equations form the foundation for working through various types of exercises, whether dealing with linear relationships, solving for variables, or interpreting graphs. Below are some of the most critical equations to master:
- Linear Equation: y = mx + b – This formula represents a straight line, where m is the slope and b is the y-intercept.
- Standard Form: Ax + By = C – A common format for linear equations, useful for solving systems of equations.
- Point-Slope Form: y – y1 = m(x – x1) – Another way to represent a line, based on a specific point (x1, y1) and the slope m.
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – Used to solve quadratic equations of the form ax² + bx + c = 0.
- Slope Formula: m = (y2 – y1) / (x2 – x1) – This formula calculates the slope between two points on a graph.
Mastering these equations will help you tackle various mathematical challenges with ease. Practice applying them in different contexts to strengthen your problem-solving skills and ensure a deeper understanding of the concepts.
How to Solve Linear Equations
Solving linear equations involves finding the value of an unknown variable that satisfies a given equation. These problems typically involve balancing both sides of the equation and isolating the variable to find its value. The process is straightforward, but requires a solid understanding of operations like addition, subtraction, multiplication, and division. Here are the basic steps for solving such equations:
| Step | Description |
|---|---|
| Step 1 | Identify the equation and isolate the variable on one side of the equation. |
| Step 2 | Simplify both sides by combining like terms if necessary. |
| Step 3 | Use inverse operations (e.g., subtract or divide) to isolate the variable completely. |
| Step 4 | Check your solution by substituting the value of the variable back into the original equation. |
For example, consider the equation 3x + 5 = 14. To solve for x:
- First, subtract 5 from both sides: 3x = 9
- Then, divide both sides by 3: x = 3
By following these steps, you can solve any linear equation systematically. Practicing these techniques will help you approach similar problems with confidence and precision.
Graphing Functions in Chapter 4
Graphing functions is an essential skill for visualizing mathematical relationships between variables. By plotting the points on a coordinate plane, you can better understand how changes in one variable affect another. In this section, the focus is on graphing linear relationships, identifying key features such as slope, intercepts, and behavior across different domains.
To graph a linear function, start by identifying the slope and y-intercept from its equation. The slope represents the rate of change, while the y-intercept is the point where the graph crosses the vertical axis. Using these two pieces of information, you can easily plot the graph and extend the line in both directions.
For example, consider the equation y = 2x + 3. The slope is 2, meaning for every increase of 1 in x, y increases by 2. The y-intercept is 3, meaning the line crosses the vertical axis at the point (0, 3). By plotting these key points and drawing the line through them, you can complete the graph.
With practice, you’ll gain the ability to graph various types of functions quickly and accurately, providing a clear visual representation of the mathematical concepts you’re working with.
Solving Word Problems in Algebra
Word problems translate real-life situations into mathematical equations that need to be solved. The key to tackling these problems is identifying the unknowns, understanding the relationships between them, and setting up the appropriate equation. Once the equation is formed, you can apply standard solving techniques to find the solution.
To solve a word problem, follow these steps:
- Read the problem carefully: Understand the scenario and identify the information provided.
- Define the variables: Decide what the unknowns represent and assign them variables.
- Translate the words into an equation: Use the relationships described in the problem to form a mathematical equation.
- Solve the equation: Apply appropriate methods (like addition, subtraction, multiplication, or division) to solve for the unknown variable.
- Check your solution: Substitute the solution back into the context of the problem to ensure it makes sense.
For example, consider the problem: “A store sells pens for $2 each and pencils for $1 each. If the total cost of 5 pens and 3 pencils is $13, how many pens and pencils were bought?”
- Let x be the number of pens and y be the number of pencils.
- The total cost can be represented by the equation: 2x + y = 13.
- From the information given, you can solve this equation to find the number of pens and pencils purchased.
By breaking the problem down into manageable steps, you can simplify even the most complex scenarios and find the solution with confidence.
Understanding Slope and Intercept
The slope and intercept are fundamental concepts when analyzing linear relationships between two variables. These two values allow you to describe how a line behaves on a graph and how the variables are related. Understanding how to identify and interpret the slope and intercept is essential for solving equations and graphing functions.
The slope represents the rate of change between the variables, indicating how much one variable changes in relation to the other. The intercept, on the other hand, shows the point where the line crosses the vertical axis, often referred to as the y-intercept. Together, these two components help form the equation of a line.
- Slope: This value shows the steepness of the line and can be calculated as the ratio of the change in the vertical direction to the change in the horizontal direction. It is often represented as m in the equation y = mx + b.
- Intercept: This value indicates where the line crosses the y-axis. It is represented as b in the equation y = mx + b.
For example, in the equation y = 3x + 2, the slope is 3, meaning for every 1 unit increase in x, y increases by 3 units. The intercept is 2, indicating that the line crosses the y-axis at the point (0, 2).
By understanding how to calculate and interpret these values, you can easily graph linear equations and gain insight into the relationships between variables in various contexts.
Common Mistakes to Avoid
When solving mathematical problems, it’s easy to make small errors that can lead to incorrect results. Identifying and correcting these mistakes early on can save time and frustration. Below are some common pitfalls to watch out for, as well as tips for avoiding them.
Misunderstanding the Problem
One of the most frequent mistakes is not fully understanding the question before starting. Always read the problem carefully and identify what is being asked. Pay attention to key details, such as what values are given and what you need to find. Skipping this step can lead to unnecessary confusion and errors later in the process.
Improper Operations
Another common mistake is performing incorrect operations, such as adding when you should be subtracting or dividing when you should be multiplying. Always double-check each step to ensure you are using the correct method for solving the equation or problem at hand.
| Mistake | Solution |
|---|---|
| Forgetting to distribute a negative sign | Ensure that when multiplying or dividing by a negative number, it is applied to each term in the equation. |
| Incorrectly solving for the variable | Check that you are isolating the variable correctly, following the proper order of operations. |
| Overlooking the units or context of the problem | Pay attention to the units given (e.g., meters, dollars) to ensure the solution makes sense in the context of the question. |
By avoiding these common errors, you can improve both your understanding and your performance when solving problems. Practicing these strategies will help you approach each problem with confidence and accuracy.
Review of Quadratic Equations

Quadratic equations are a type of polynomial equation that plays a key role in various areas of mathematics. These equations involve the square of a variable and often have two possible solutions. Understanding how to solve and analyze quadratic equations is crucial for advancing in mathematical problem-solving.
Standard Form of a Quadratic Equation
The general form of a quadratic equation is:
- ax² + bx + c = 0
Where a, b, and c are constants, and x is the variable. The value of a determines the direction of the parabola (whether it opens upwards or downwards), while b and c affect the position of the curve.
Methods for Solving Quadratic Equations
There are several methods for solving quadratic equations, including factoring, completing the square, and using the quadratic formula:
- Factoring: This method involves rewriting the quadratic equation as a product of two binomials. This is possible when the equation is factorable.
- Completing the Square: This technique involves rewriting the quadratic expression so that one side of the equation is a perfect square trinomial, making it easier to solve for x.
- Quadratic Formula: This formula x = (-b ± √(b² – 4ac)) / 2a provides a solution for any quadratic equation, even when factoring is not possible.
For example, for the equation x² + 6x + 9 = 0, it can be factored as (x + 3)(x + 3) = 0, giving the solution x = -3.
Quadratic equations are versatile and appear in various real-life situations, such as projectile motion, optimization problems, and more. Mastering the techniques for solving these equations is essential for further progress in mathematics.
Steps for Simplifying Expressions
Simplifying expressions is a critical skill that helps in solving mathematical problems more efficiently. By reducing complex expressions to their simplest form, you can make calculations faster and more accurate. The goal is to combine like terms and perform operations in a systematic way, making the expression easier to handle.
Identifying Like Terms
The first step in simplifying an expression is identifying like terms. Like terms are terms that have the same variable raised to the same power. For example, 3x and 5x are like terms because both contain the variable x. These terms can be combined.
Combining Like Terms
Once like terms are identified, combine them by adding or subtracting their coefficients. This process eliminates unnecessary complexity. For example:
- 3x + 5x = 8x
- 4y – 2y = 2y
After combining the like terms, the expression becomes simpler and easier to work with. In some cases, further operations such as factoring or distributing may be required to fully simplify the expression.
Remember to always check for any common factors or operations that can further reduce the expression. Following these steps ensures that you arrive at the most simplified version of the original expression.
Factoring in Algebra 1 Chapter 4
Factoring is an essential technique used to simplify expressions and solve equations. It involves breaking down an expression into smaller components, or factors, that when multiplied together yield the original expression. Understanding the process of factoring is vital for solving quadratic equations and simplifying polynomial expressions.
Common Methods of Factoring
There are several methods used to factor polynomials, depending on the structure of the expression. The most common methods include:
- Factoring by Grouping: This method involves grouping terms in pairs and factoring out the greatest common factor (GCF) from each group.
- Factoring Trinomials: Trinomials can often be factored into two binomials. The goal is to find two numbers that multiply to give the constant term and add to give the middle coefficient.
- Difference of Squares: This method is used when the expression is a difference between two squares, such as x² – 16, which factors as (x – 4)(x + 4).
Example of Factoring a Quadratic Expression
Consider the quadratic expression x² + 7x + 10. To factor this expression:
- Find two numbers that multiply to give 10 and add to give 7. These numbers are 2 and 5.
- Write the factored form as (x + 2)(x + 5).
Thus, the factored form of the quadratic expression x² + 7x + 10 is (x + 2)(x + 5).
Factoring Table
| Expression | Factored Form |
|---|---|
| x² + 5x + 6 | (x + 2)(x + 3) |
| x² – 9 | (x – 3)(x + 3) |
| x² + 4x + 4 | (x + 2)(x + 2) |
By practicing these techniques and methods, you can become proficient in factoring various types of expressions and solving quadratic equations more easily.
Tips for Test Preparation
Preparing for a math exam can be overwhelming, but with the right approach, you can tackle the material effectively and boost your confidence. Proper preparation involves understanding key concepts, practicing problem-solving, and developing a strategy for the test itself. A focused approach can significantly improve your performance on the exam.
Review Key Concepts
Before diving into practice problems, ensure you have a solid grasp of the main ideas covered in your coursework. Review your notes, textbooks, or any materials provided to identify important formulas, rules, and methods. Focus on understanding the reasoning behind each concept rather than just memorizing formulas.
- Identify areas where you feel less confident and spend extra time reinforcing those topics.
- Use mnemonic devices or visual aids to remember key formulas and definitions.
- Write summaries of each concept to solidify your understanding.
Practice with Sample Problems
Hands-on practice is crucial for mastering mathematical techniques. Work through a variety of problems similar to those you expect to encounter on the test. This will help you become more comfortable with the problem-solving process and identify any areas where you may need additional review.
- Start with simpler problems and gradually increase the difficulty level as you gain confidence.
- Time yourself to simulate the actual testing environment.
- After solving a problem, review the solution to ensure you understand each step.
By combining focused review and consistent practice, you will improve your readiness for the exam and enhance your ability to tackle questions with ease.
How to Use the Distributive Property
The distributive property is a fundamental rule in mathematics that allows you to simplify expressions by breaking them down into smaller, more manageable parts. It is particularly useful when you have terms within parentheses and need to multiply them by an outside number. By applying this property, you can simplify complex equations and make calculations easier to handle.
Basic Steps for Applying the Property
To use this property, you must multiply each term inside the parentheses by the number outside. Here’s the process:
- Identify the number outside the parentheses and the terms inside.
- Multiply the outside number by each term inside the parentheses.
- Combine like terms if needed.
For example, in the expression 3(x + 4), you would multiply 3 by both x and 4, resulting in 3x + 12.
Examples of Applying the Property
Here are some examples that show the distributive property in action:
- 2(a + b) = 2a + 2b
- 5(3x – 4) = 15x – 20
- -4(2y + 5) = -8y – 20
By mastering this technique, you can simplify expressions with multiple terms, making it easier to solve problems and equations.
Understanding Systems of Equations
A system of equations consists of two or more equations that share common variables. The goal is to find values for these variables that satisfy all of the equations simultaneously. Systems can involve linear equations, where the variables appear to the first power, and the solutions often represent points of intersection on a graph. These solutions can be found using various methods, such as substitution, elimination, or graphical representation.
Types of Systems
There are three main types of systems that can occur:
- Consistent system: Has one or more solutions, meaning the equations intersect at one or more points.
- Inconsistent system: Has no solution, as the equations represent parallel lines that never meet.
- Dependent system: Has infinitely many solutions, as the equations represent the same line, making all points on the line solutions.
Methods for Solving Systems
To solve a system, several methods can be used depending on the complexity of the equations:
- Substitution: Solve one equation for one variable and substitute that expression into the other equation.
- Elimination: Add or subtract the equations to eliminate one of the variables, making it easier to solve for the remaining one.
- Graphing: Plot both equations on a graph and identify the point of intersection, which represents the solution.
By understanding the different types of systems and the methods for solving them, you can efficiently find solutions to complex problems involving multiple relationships between variables.
Real-World Applications of Algebra
The concepts learned in mathematical courses can be applied in various real-world situations. From personal finance to engineering, understanding the relationships between variables is crucial for problem-solving. These techniques help in optimizing resources, making predictions, and analyzing data. In many fields, the ability to create models based on known information can lead to more efficient solutions and innovations.
Applications in Business and Economics
Mathematical relationships are commonly used in business for tasks such as budgeting, cost analysis, and profit forecasting. By using equations, companies can determine how changes in one area, such as product pricing or production volume, affect overall performance. For example:
- Cost analysis: Businesses can calculate total production costs based on fixed costs and variable expenses.
- Break-even analysis: This helps companies determine the point at which total revenue equals total costs, guiding pricing strategies.
Applications in Engineering and Technology
In engineering fields, mathematical models are used to design structures, systems, and products. Engineers use relationships between quantities to predict outcomes and ensure safety and efficiency. Some examples include:
- Structural design: Engineers use equations to calculate forces acting on buildings, bridges, and other structures.
- Technology development: Understanding relationships between variables allows developers to improve processes, such as optimizing computer algorithms or enhancing data storage systems.
In all these cases, the application of mathematical reasoning helps professionals make informed decisions, ensuring more reliable results and innovative solutions.
Practice Problems and Solutions
Working through problems is an essential way to reinforce concepts and gain a deeper understanding of mathematical principles. By tackling various exercises, students can strengthen their problem-solving skills, identify areas where they may need more practice, and become more confident in their ability to apply what they’ve learned. Below are a few examples of typical problems and their step-by-step solutions.
Problem 1: Solve for x
Equation: 3x + 5 = 20
Solution:
- Start by isolating the variable. Subtract 5 from both sides: 3x = 15.
- Now, divide both sides by 3: x = 5.
- The solution is x = 5.
Problem 2: Simplify the Expression
Expression: 4(2x – 3) + 5x
Solution:
- First, distribute the 4: 4 * 2x – 4 * 3 = 8x – 12.
- Now add the 5x: 8x + 5x = 13x.
- So the simplified expression is 13x – 12.
Problem 3: Graph the Equation
Equation: y = 2x + 3
Solution:
- Start by plotting the y-intercept (0, 3) on the graph.
- Next, use the slope of 2 to find the next point. From (0, 3), move up 2 units and to the right 1 unit to reach (1, 5).
- Draw a line through the points (0, 3) and (1, 5). This is the graph of the equation.
By solving problems like these, you can improve your skills and ensure a solid grasp of the concepts. Practice regularly to master the material and prepare for future challenges.