
Mastering complex concepts can be a challenge, especially when it comes to arithmetic and problem-solving tasks. Understanding how to approach different types of exercises and recognizing the logic behind each solution is essential for building confidence and competence in mathematics.
By reviewing the solutions to these exercises, students can reinforce their learning and gain a deeper understanding of the process. This guide offers insights into solving problems, along with detailed explanations that help clarify common areas of confusion. Whether you are reviewing past lessons or preparing for future topics, the goal is to improve critical thinking and enhance problem-solving skills.
Learning to approach each challenge step by step is key to developing a strong foundation. As students work through various problems, it’s important to focus on the reasoning behind each answer, not just the final result. Emphasizing this approach leads to better long-term retention and mastery of essential skills.
6th Grade Math Module 5 Answer Key

When tackling problem-solving challenges, having access to the correct solutions is essential for reinforcing learning and ensuring that concepts are understood. Reviewing the solutions not only helps identify where mistakes were made but also provides clarity on how to approach similar problems in the future. The following section provides detailed solutions for a variety of exercises and guides students through each step of the process.
By breaking down each problem, students can see the logical steps involved, making it easier to apply the same strategies to new challenges. Below is a breakdown of the types of exercises typically covered in this set of lessons:
- Understanding basic operations and their relationships
- Working with fractions and decimals
- Identifying patterns and solving word problems
- Applying mathematical reasoning to real-world situations
Each solution is presented in a clear, easy-to-follow format, highlighting the key steps required to arrive at the correct outcome. Whether it’s simple addition or more complex problem-solving, breaking down each solution will help ensure better understanding and retention of the material.
For each question, the steps taken to solve it are outlined in detail:
- Start by identifying the problem’s requirements.
- Break the problem into manageable parts.
- Apply relevant mathematical rules and concepts.
- Review the solution to check for accuracy.
This structured approach not only makes solving problems easier but also builds critical thinking skills that are applicable across various topics. Keep practicing, and soon the logic behind these exercises will become second nature.
Understanding the Key Concepts of Module 5
To succeed in solving mathematical problems, it’s crucial to grasp the foundational ideas that each set of exercises is built upon. These concepts form the building blocks for more advanced topics, and understanding them thoroughly will make future lessons easier to tackle. This section covers the essential topics that students need to focus on to ensure they are prepared to solve a wide range of problems with confidence.
Mastering Operations with Fractions and Decimals
One of the core areas covered in this set of lessons involves working with fractions and decimals. Students will encounter problems that require them to add, subtract, multiply, and divide these numbers. Understanding how to convert between fractions and decimals, and how to handle operations involving both, is critical for mastering this section.
Recognizing Patterns and Problem Solving
Another important concept is the ability to identify patterns and use them to solve word problems. Recognizing mathematical relationships between numbers allows students to approach problems more strategically. Whether the task involves solving for unknowns or applying known formulas, identifying the underlying pattern is often the key to finding the correct solution.
By focusing on these key areas, students will be well-equipped to tackle a variety of exercises and continue to build their mathematical understanding. Mastery of these concepts not only helps in academic success but also in applying math to everyday situations.
How to Use the Answer Key Effectively
Accessing the correct solutions is a valuable tool for reinforcing your learning and ensuring you understand the problem-solving process. However, it’s important to use the solutions not just as a reference, but as a guide to improve your approach to similar challenges. Here are some strategies to make the most out of reviewing the correct solutions.
Review Step-by-Step
Rather than simply checking your final result, go through each step of the solution to understand how it was derived. This helps you recognize the logical flow and reasoning behind each part of the problem. Follow these steps:
- Identify how the problem was broken down.
- Understand the method used to solve it.
- Note any patterns or shortcuts that can be applied to future exercises.
Learn from Mistakes
If your solution differs from the correct one, don’t just move on. Take the time to figure out where you made an error. Ask yourself these questions:
- Did I misunderstand the problem’s requirements?
- Did I make a calculation mistake?
- Did I apply the correct method to solve it?
By identifying where things went wrong, you can correct your approach and avoid similar mistakes in the future. Using the solution as a learning tool, rather than just a verification, will significantly improve your problem-solving skills.
Common Mistakes in Module 5 Math
When working through mathematical problems, it’s easy to make small mistakes that can lead to incorrect results. These errors often stem from misunderstandings of the process, rushing through steps, or overlooking important details. Recognizing these common mistakes is the first step toward avoiding them and improving problem-solving skills.
Some frequent errors include:
- Misunderstanding the problem’s requirements, leading to incorrect operations.
- Forgetting to simplify fractions or decimals when necessary.
- Applying the wrong method for solving a word problem.
- Overlooking negative signs or miscalculating them during addition or subtraction.
- Failing to check work after completing each step.
By carefully reviewing each problem and taking the time to recheck work, students can reduce the likelihood of these mistakes. Focusing on the process, rather than just the final answer, ensures that the correct method is used consistently and that the logic behind the solution is fully understood.
Practice Problems for Module 5 Review
Reinforcing what you’ve learned through practice is essential for building a strong understanding of the concepts. Working through additional problems allows you to apply the techniques you’ve learned and identify any areas that need more attention. Below are a few problems designed to help solidify your knowledge and prepare you for future challenges.
| Problem | Solution |
|---|---|
| Simplify the fraction 12/16. | 12/16 = 3/4 |
| Add 0.75 + 1.25. | 0.75 + 1.25 = 2.00 |
| Find the product of 3/4 and 2/5. | (3/4) × (2/5) = 6/20 = 3/10 |
| Subtract 5/6 from 7/6. | 7/6 – 5/6 = 2/6 = 1/3 |
| Solve the word problem: A store sells pencils in packs of 6. If you buy 4 packs, how many pencils do you have? | 4 packs × 6 pencils = 24 pencils |
By practicing these problems, students can improve their understanding of key concepts and become more confident in solving similar exercises. Take time to work through each problem carefully, and always check your results to ensure accuracy.
Step-by-Step Solutions for Each Question
To truly understand how to solve a problem, it’s important to break down the process into clear, manageable steps. By carefully following each stage of the solution, students can ensure they are applying the correct methods and reasoning. This section provides detailed, step-by-step instructions for solving various types of problems, offering a clear path from start to finish.
Below is a step-by-step breakdown for solving some typical problems:
- Problem 1: Simplify the fraction 18/24
- Step 1: Identify the greatest common divisor (GCD) of 18 and 24, which is 6.
- Step 2: Divide both the numerator and the denominator by 6.
- Step 3: Simplified fraction = 18 ÷ 6 / 24 ÷ 6 = 3/4.
- Step 1: Line up the decimal points.
- Step 2: Add each column starting from the rightmost digit.
- Step 3: The sum is 1.45 + 3.55 = 5.00.
- Step 1: First, solve the expression inside the parentheses: 3 + 2 = 5.
- Step 2: Multiply 5 × 5 = 25.
- Step 1: Convert 5/4 into an improper fraction: 5/4 = 10/8.
- Step 2: Subtract 10/8 – 7/8 = 3/8.
- Step 1: Multiply the number of cookies baked per hour by the total number of hours: 12 × 5 = 60.
By following each step in sequence, students can see how each operation is performed and learn how to approach similar problems on their own. Understanding the process behind the solution is key to mastering the material and building confidence in problem-solving skills.
Tips for Mastering Module 5 Topics
To truly excel in solving problems, it’s essential to develop a strong understanding of the key concepts and strategies used in each topic. By consistently practicing, breaking down problems, and applying the right techniques, you’ll be able to confidently tackle even the most challenging exercises. Here are some practical tips to help reinforce your knowledge and improve your problem-solving skills.
Below are some helpful strategies for mastering the topics covered:
| Tip | Description |
|---|---|
| Understand the Basics | Ensure you have a solid grasp of foundational concepts like fractions, decimals, and basic operations before moving on to more complex problems. |
| Break Down Problems | Divide each problem into smaller, more manageable parts. Solving step by step helps reduce errors and clarifies your thinking. |
| Practice Regularly | Consistent practice is key to mastering any skill. Solve different types of problems to strengthen your understanding and retention. |
| Check Your Work | Always review your solutions to ensure accuracy. Recheck your steps, especially for tricky calculations or word problems. |
| Learn from Mistakes | Whenever you make an error, take the time to understand why it happened and how you can correct it. This helps avoid similar mistakes in the future. |
By following these tips and remaining committed to practice, you’ll be well on your way to mastering the key topics and solving problems with confidence. Keep reviewing and refining your techniques, and don’t hesitate to revisit earlier concepts if necessary. Mastery comes with consistent effort and a willingness to learn from each experience.
How Module 5 Prepares for Future Lessons
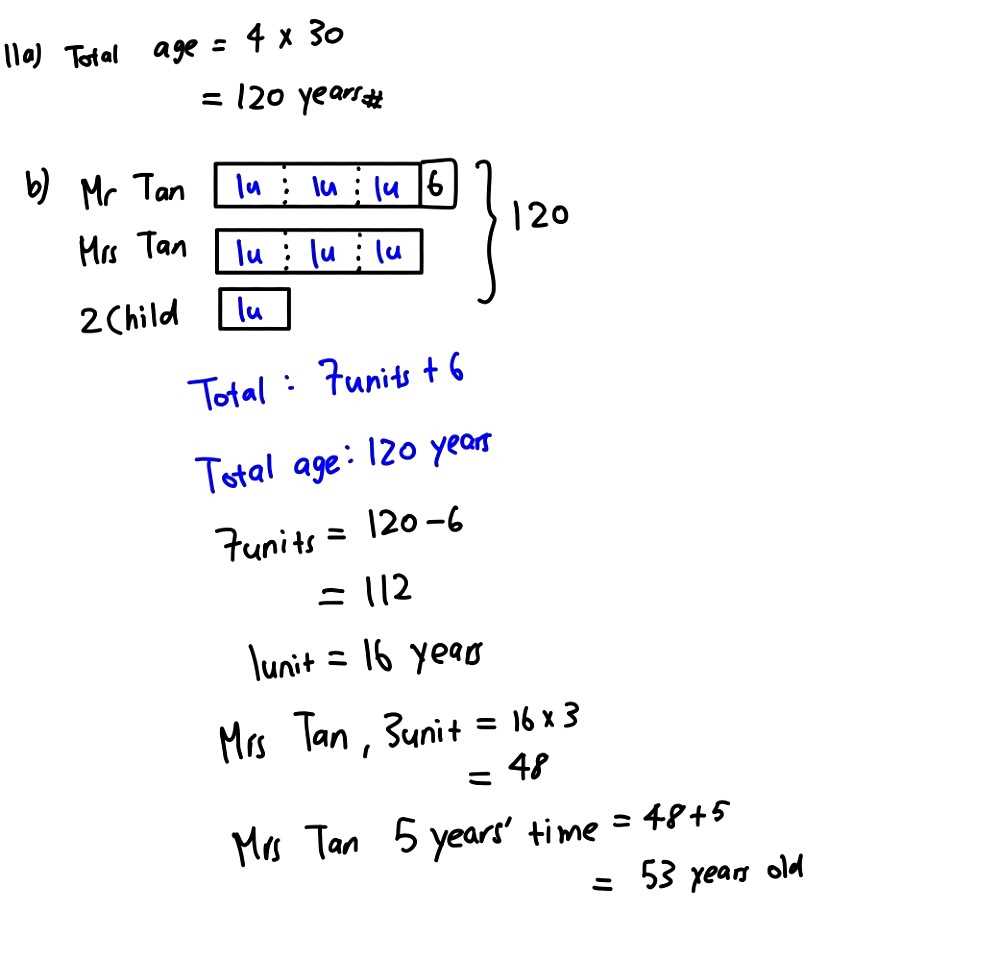
The concepts covered in this section lay a strong foundation for more advanced topics that will be explored in later lessons. By mastering the key skills and strategies now, students build the confidence and ability to tackle more complex problems in the future. The approach taken in this chapter provides the necessary tools for success in subsequent learning, making it an essential stepping stone in overall academic development.
As students gain proficiency in the topics of this section, they develop critical thinking and problem-solving skills that will be vital in later lessons. The ability to work with fractions, decimals, and word problems paves the way for more intricate mathematical concepts, such as ratios, proportions, and advanced equations. Each problem solved reinforces the underlying principles that will be applied to higher-level material, ensuring that students are prepared to face new challenges with a solid understanding of core concepts.
Additionally, the structured learning within this section helps students improve their logical reasoning, attention to detail, and ability to analyze complex situations–skills that will serve them well in future lessons, not only in mathematics but across various subjects as well.
Real-Life Applications of Module 5 Math
The skills learned in this section are not just theoretical; they have numerous practical applications in everyday life. Understanding how to work with numbers, fractions, and simple calculations helps individuals make informed decisions in many real-world situations. These concepts are used in various fields, from personal finance to cooking, to even planning a trip. By seeing how these lessons translate into daily tasks, students gain a better appreciation of their importance and usefulness.
For example, when managing a budget, understanding how to calculate percentages, add fractions, or work with decimals allows individuals to plan their finances effectively. Whether it’s determining the cost of items on sale or splitting a bill among friends, the ability to apply basic arithmetic is crucial for making practical decisions.
In the kitchen, recipes often require adjusting measurements. Knowing how to multiply or divide fractions is essential for scaling recipes up or down. Similarly, understanding time and measurements is crucial in various crafts, DIY projects, and construction tasks, where accuracy and precision matter.
These everyday applications highlight the importance of mastering these concepts, as they enable individuals to navigate the world around them with confidence and ease. The skills developed now are foundational to making calculations quickly and accurately, which will be beneficial in both personal and professional contexts in the future.
How to Check Your Work in Module 5

Ensuring accuracy in your calculations is a vital skill for problem-solving. It’s essential to check your work regularly to avoid simple mistakes that can lead to incorrect answers. By following a systematic approach, you can verify each step of your process and feel confident in your results. Below are some effective strategies to help you review and validate your work.
Step-by-Step Review
One of the most reliable ways to check your work is to go through each step carefully and confirm that you’ve followed the correct method. This can help catch any overlooked mistakes.
- Start by reviewing the problem statement to ensure you understand what is being asked.
- Check each operation you performed, whether it’s adding, subtracting, multiplying, or dividing.
- Confirm that the calculations were done in the right order, particularly for more complex problems that involve multiple steps.
- Ensure that you have applied any necessary rules or formulas correctly.
Double-Check Your Final Answer
After completing all the steps, it’s a good idea to recheck your final solution. Often, simple errors occur at the end, like misplacing a decimal point or a sign.
- Look over your final result and make sure it makes sense in the context of the problem.
- Try a different method to solve the problem if possible, to see if you reach the same conclusion.
- If the problem involves measurements, units, or fractions, ensure you have simplified or converted them correctly.
By carefully reviewing each step and validating your final solution, you can identify any errors and correct them, ensuring a more accurate outcome.
Guidance for Parents Helping with Module 5
Supporting a child’s learning can be a rewarding experience, especially when the concepts seem challenging. Parents play a key role in helping students navigate new material and build confidence in their abilities. Understanding how to assist effectively in their studies can make a significant difference in their progress. The following tips provide guidance on how parents can support their children in mastering the concepts of this section.
Foster a Positive Learning Environment

Creating a quiet, comfortable space for studying can help students focus better on their tasks. Ensure that your child has all necessary materials, such as pencils, paper, and a calculator, to avoid distractions. It’s also helpful to establish a regular study routine so that your child knows when to expect focused learning time.
- Encourage your child to ask questions if they don’t understand something.
- Provide reassurance that making mistakes is part of the learning process and help them view challenges as opportunities for growth.
- Be patient and avoid overwhelming your child with too much information at once.
Be Involved Without Taking Over

While it’s important to be present and available to assist with the work, it’s equally important to encourage your child to take responsibility for their learning. Guide them through problems, but allow them to attempt solutions independently before offering help.
- Use open-ended questions to prompt thinking, such as “How could you approach this problem?” or “What steps do you think we should take first?”
- If they are stuck, break the problem into smaller, manageable parts to help them see the solution step by step.
- Provide examples of similar problems, but avoid giving away the answers.
With these strategies, parents can offer meaningful support while empowering their children to develop problem-solving skills and gain mastery over the material.
Key Vocabulary in Module 5 Math
Understanding the terminology used in this section is crucial for grasping the concepts and solving problems effectively. The specific terms introduced here form the foundation for a deeper comprehension of the subject matter and help students communicate their reasoning clearly. Below are some of the essential terms to focus on as you work through the lessons.
Important Terms to Know
Familiarity with key terms will aid in better understanding and application of the lessons. These terms often appear in both problem descriptions and solutions, making it essential to know their meanings.
| Term | Definition |
|---|---|
| Fraction | A number that represents a part of a whole, expressed as a numerator and denominator. |
| Decimal | A number expressed in the base 10 system, often used to represent parts of a whole. |
| Percentage | A way of expressing a number as a fraction of 100, often used to compare ratios. |
| Product | The result of multiplying two numbers together. |
| Sum | The result of adding two or more numbers. |
| Difference | The result of subtracting one number from another. |
How to Use These Terms

In practical use, these terms help describe the relationships between numbers and how they interact. For example, understanding how to work with fractions and decimals is essential when comparing values or solving problems that involve division or multiplication. Percentages are frequently used in real-life applications, such as calculating discounts or determining proportions. By mastering these terms, students can approach more complex problems with confidence.
Overcoming Challenges in Module 5 Exercises

When tackling exercises in this section, students may encounter difficulties that can hinder their progress. It is common to feel overwhelmed when faced with complex problems or unfamiliar concepts. However, by adopting the right strategies and mindset, these challenges can be transformed into valuable learning opportunities. Understanding how to approach these problems methodically is key to overcoming obstacles and achieving success.
One of the first steps in overcoming challenges is recognizing when a problem is difficult. This awareness allows students to break the problem into smaller, more manageable parts. Additionally, understanding the root of the challenge–whether it’s a specific concept or a step in the process–helps direct focus and effort more effectively.
Here are some helpful strategies to keep in mind:
- Revisit the Basics: Often, the struggle comes from not fully understanding foundational concepts. Reviewing simpler exercises or previous sections can help reinforce these basics.
- Break Problems Down: Instead of trying to solve everything at once, break complex problems into smaller steps. This makes it easier to tackle each part without feeling overwhelmed.
- Use Visual Aids: Diagrams, charts, or even drawing out the problem can offer a clearer understanding and make abstract concepts more tangible.
- Ask for Help: Don’t hesitate to seek assistance from teachers, peers, or even online resources. Sometimes, a different perspective can make a significant difference in understanding.
By applying these strategies and maintaining a positive attitude, students can conquer any challenges they face in the exercises and deepen their understanding of the material.
Interactive Resources for Module 5 Success
To achieve success in this section, using interactive resources can significantly enhance comprehension and retention. These tools provide a dynamic way to engage with the material, offering immediate feedback and step-by-step explanations. By incorporating various online platforms and interactive exercises, students can better visualize concepts and reinforce their understanding in a fun and engaging way.
Interactive resources provide a more hands-on approach to learning, helping to bridge the gap between theoretical knowledge and practical application. Whether through quizzes, simulations, or interactive worksheets, these tools create opportunities for active learning and immediate correction of mistakes.
Benefits of Interactive Tools
- Instant Feedback: Immediate feedback helps students identify mistakes and learn from them right away, making it easier to correct misunderstandings.
- Variety of Learning Formats: Interactive platforms often offer multiple ways to engage with the material, such as videos, games, and challenges, catering to different learning styles.
- Self-Paced Learning: Students can work through the exercises at their own pace, ensuring that they fully understand each concept before moving forward.
Recommended Interactive Tools
- Online Practice Platforms: Websites like Khan Academy, IXL, and Quizlet offer interactive lessons and quizzes that cover a range of topics.
- Interactive Simulations: Tools like PhET Interactive Simulations provide visual and hands-on experiences to understand concepts better.
- Virtual Flashcards: Create custom flashcards on platforms like Anki or Quizlet to reinforce key terms and equations.
Using these interactive resources effectively can greatly enhance learning outcomes, providing students with the tools they need to master the material and succeed in their exercises.
How Module 5 Relates to Other Math Topics
The content explored in this section connects to various other mathematical areas, providing a foundation for more advanced concepts. Understanding the principles here is essential as it builds on previous knowledge and sets the stage for future topics. The key to mastering this section lies in recognizing how it integrates with other topics, reinforcing skills that will be vital later on.
As students progress through their studies, the concepts introduced in this section will help them approach more complex problems in algebra, geometry, and beyond. By grasping these connections, learners are better equipped to understand and solve real-world problems that require a blend of multiple mathematical skills.
Connecting with Other Key Topics

- Fractions and Decimals: A deep understanding of this section provides the foundation for working with fractions and decimals in later studies, making it easier to solve problems involving these concepts.
- Algebraic Thinking: Concepts introduced here support the transition into algebra, where operations and problem-solving strategies from this section are expanded and applied to unknown variables.
- Measurement: This section also helps develop an understanding of measurement units and conversions, which are essential for more advanced topics in geometry and real-world applications.
Real-World Applications

- Budgeting and Financial Literacy: Skills learned here can be applied to budgeting, such as calculating costs and understanding pricing structures in everyday life.
- Science and Engineering: The concepts explored are foundational for further learning in areas like physics and engineering, where precise measurements and calculations are key to problem-solving.
- Data Analysis: Understanding relationships between numbers prepares students for statistical analysis and interpreting data in fields such as social science or economics.
Mastering the topics in this section is not only important for immediate learning, but it also strengthens the ability to solve problems in many future mathematical disciplines. The interconnectedness of the concepts learned here enables students to approach more advanced topics with confidence.
Benefits of Practicing Module 5 Regularly
Consistent practice is one of the most effective ways to reinforce learning and deepen understanding of the concepts explored in this section. By engaging with the material on a regular basis, students can build confidence, improve problem-solving skills, and achieve long-term mastery. The more frequently learners revisit the exercises, the better they are at recognizing patterns and applying strategies to new challenges.
Regular practice not only strengthens memory but also enhances critical thinking. As students work through different types of problems, they develop a better understanding of how to approach complex questions and refine their ability to analyze solutions systematically. This approach promotes a more thorough grasp of the material, which is essential for mastering future topics and tackling more advanced lessons with ease.
Here are some key advantages of practicing the content frequently:
- Increased Retention: Repetition helps solidify information in long-term memory, making it easier to recall key concepts when needed.
- Enhanced Problem-Solving: Regular exposure to various types of exercises sharpens reasoning and analytical skills, preparing students for more challenging tasks.
- Improved Confidence: As students practice and see their progress, they gain confidence in their abilities, leading to a positive mindset for tackling new topics.
- Better Time Management: The more practice students get, the faster they become at identifying patterns and solving problems, improving their efficiency.
- Stronger Understanding: Working through the exercises repeatedly allows students to see the connections between different concepts, providing a more comprehensive understanding of the subject.
Incorporating regular practice into the study routine not only helps with immediate learning but also prepares students for future academic success. The benefits of consistent engagement extend beyond the classroom, equipping learners with valuable skills that will serve them in various fields of study and real-world scenarios.