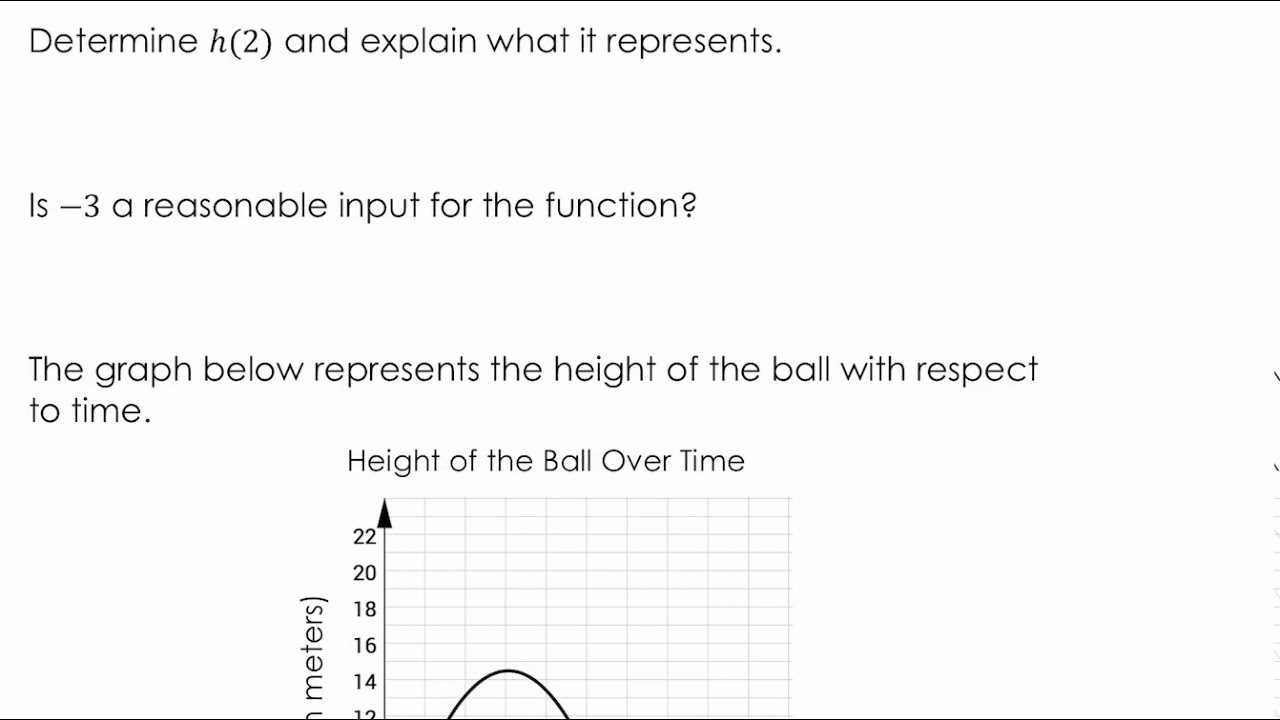
Understanding mathematical principles is a crucial step toward developing logical thinking and problem-solving skills. This part of the curriculum focuses on providing students with the tools they need to decode complex ideas and tackle challenging exercises effectively. The emphasis is on building a solid foundation that allows for deeper comprehension and long-term success in related topics.
The material introduces methods that simplify intricate calculations, making it easier to approach and resolve real-world scenarios. By exploring various strategies and techniques, learners can enhance their analytical abilities and gain the confidence needed to excel in their studies. The practical applications included offer valuable insights into how these principles can be used beyond the classroom.
Whether you are reviewing fundamentals or exploring advanced concepts, this guide is designed to assist in overcoming hurdles and refining your approach. The structured lessons and examples are tailored to support a wide range of learning styles, ensuring that every student finds the process engaging and informative.
Comprehensive Guide to Section Two
This part of the study material is crafted to strengthen your understanding of foundational concepts and their practical applications. It focuses on providing clarity to intricate ideas while enhancing problem-solving strategies. By breaking down complex tasks into manageable steps, learners can approach challenges with greater ease and confidence.
The topics covered in this guide include essential techniques, logical reasoning methods, and efficient ways to interpret and solve problems. The material integrates theoretical knowledge with practical exercises, ensuring that students not only learn but also apply what they have studied effectively.
| Topic | Description | Skills Developed | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Core Principles | Focus on basic concepts and their importance in solving problems. |
| Operation | Inverse Operation |
|---|---|
| Addition | Subtraction |
| Multiplication | Division |
| Exponentiation | Taking the root |
By applying these methods, the process of solving linear equations becomes much more straightforward, allowing you to handle increasingly complex problems with confidence.
Applying Mathematical Concepts in Daily Life
Mathematics is not just a subject learned in school; it is a vital tool used in everyday life. The principles of solving problems and recognizing patterns can be applied to a variety of real-world situations. Whether you’re budgeting, planning a trip, or cooking, mathematical skills help in making informed decisions and solving everyday challenges.
One of the most practical aspects of learning mathematical principles is recognizing how often they are used in daily activities. Here are a few ways these concepts are applied in real-life scenarios:
Managing Personal Finances
Calculating expenses, savings, and understanding loan interest are common tasks where mathematical skills come into play. Whether managing a household budget or planning for a large purchase, using formulas and basic operations can help make decisions clearer.
- Budgeting: Keeping track of income and expenditures is easier when using simple addition and subtraction.
- Loan Calculation: Understanding interest rates and payment schedules involves using equations to ensure the best deal.
- Investment Planning: Compounding interest and returns can be calculated to assess potential financial growth.
Everyday Problem Solving
From cooking to home repairs, understanding how to apply simple calculations can make tasks much simpler. Here are some examples:
- Cooking: Adjusting ingredient proportions in a recipe based on the number of servings requires the use of ratios and multiplication.
- Home Improvements: Determining the area of a room for painting or flooring involves applying multiplication and division to find dimensions.
- Travel Planning: Estimating travel time, fuel costs, and routes requires basic calculation skills to optimize plans.
By integrating these basic mathematical skills into daily routines, individuals can make more efficient decisions and solve problems more effectively.
Review of Commonly Used Formulas
Understanding fundamental formulas is essential for solving mathematical problems effectively. These formulas serve as the building blocks for a variety of tasks, from calculating areas and volumes to solving equations. By familiarizing oneself with these essential equations, individuals can improve their ability to handle a range of mathematical challenges with confidence.
Below is a collection of commonly used formulas that are often encountered in various mathematical problems:
- Area of a Rectangle:
Area = Length × Width
This formula is used to find the surface area of rectangular spaces, from rooms to paper sheets.
- Area of a Triangle:
Area = ½ × Base × Height
This equation calculates the area of a triangle, whether for geometry problems or practical applications like land measurement.
- Perimeter of a Rectangle:
Perimeter = 2 × (Length + Width)
Used to determine the boundary length of a rectangular object, this formula is important for tasks such as fencing or framing.
- Quadratic Formula:
x = (-b ± √(b² – 4ac)) / 2a
This is a standard equation used for solving quadratic equations, essential in fields like physics and engineering.
- Volume of a Cube:
Volume = Side³
This formula is used to calculate the amount of space within a cube, commonly used in real-world scenarios such as packaging or construction.
- Slope of a Line:
Slope = (y₂ – y₁) / (x₂ – x₁)
The slope formula calculates the steepness of a line between two points and is crucial for understanding relationships in graphs and charts.
These formulas are just the starting point for problem-solving in mathematics. Mastering them can significantly enhance your ability to approach both theoretical and practical challenges efficiently.
Building Skills Through Targeted Exercises
Developing proficiency in solving mathematical challenges requires focused practice. Engaging in exercises designed to target specific concepts helps reinforce understanding and builds problem-solving abilities. These exercises allow individuals to hone their skills progressively, leading to a deeper grasp of key principles and techniques. By consistently working through problems that focus on particular areas, learners can gain confidence and improve their overall performance.
Here are some strategies for effectively utilizing targeted exercises to strengthen skills:
- Focus on One Concept at a Time:
Concentrating on one idea at a time ensures thorough understanding before moving on to the next. This approach allows learners to master each skill step-by-step.
- Vary the Difficulty Level:
Start with simpler problems to build a solid foundation, and gradually increase the complexity as your skills improve. This progression helps maintain motivation while challenging growth.
- Practice with Real-World Applications:
Applying mathematical concepts to everyday situations can make abstract ideas more relatable and easier to understand. For example, budgeting or measurement tasks can be great ways to practice.
- Track Progress Over Time:
Keep track of your improvement by regularly revisiting exercises and noting areas of growth. Reviewing mistakes is also a key part of the learning process, as it helps identify areas for further focus.
By incorporating these techniques into your practice routine, you can effectively build and refine your mathematical skills, leading to greater mastery and confidence in tackling challenges.
Identifying Errors in Problem Solutions
Recognizing mistakes in problem-solving is an essential skill that improves overall understanding and accuracy. Errors can occur at various stages of the problem-solving process, from interpreting the question to performing calculations. Identifying these mistakes early on is key to improving problem-solving abilities and avoiding repeated errors. By learning how to detect common pitfalls, individuals can refine their approach and increase their success rate in solving similar challenges.
Common Types of Mistakes

Several types of errors often appear during problem-solving tasks. Recognizing them can help prevent future issues:
- Calculation Errors: Mistakes can occur when performing arithmetic operations, such as adding, subtracting, multiplying, or dividing incorrectly. Double-checking each calculation is a good practice to avoid these mistakes.
- Misinterpretation of the Problem: Sometimes, the issue arises from a misunderstanding of the problem itself. Ensuring that all parts of the question are correctly understood before proceeding can help avoid incorrect assumptions.
- Incorrect Application of Formulas: Applying the wrong formula or using it incorrectly can lead to erroneous results. It’s important to verify that the correct formula is used for the given problem and that it is applied step-by-step.
Strategies for Identifying Mistakes

To minimize errors and improve problem-solving accuracy, consider the following approaches:
- Work Through the Problem Step-by-Step: Break down each problem into smaller, manageable steps. This approach makes it easier to spot where an error might have occurred.
- Check Your Work: After solving a problem, review each step carefully to ensure the process is correct. Revisiting the question and solution can help you identify any overlooked mistakes.
- Use Different Methods: Try solving the same problem using an alternative approach. This can offer a new perspective and help spot any inconsistencies in your solution.
By incorporating these strategies into your routine, you can enhance your ability to identify and correct errors, improving your overall problem-solving efficiency.
Utilizing Online Tools for Better Learning
In the digital age, the internet offers a vast array of resources to enhance learning and improve understanding of various concepts. By leveraging the power of online tools, learners can access interactive exercises, detailed tutorials, and helpful visual aids that make complex topics more approachable. These tools provide the opportunity for personalized learning experiences, allowing students to work at their own pace and gain deeper insights into the material they are studying.
Types of Online Tools
There are several types of online resources that can help reinforce learning:
- Interactive Simulations: These tools allow learners to experiment with different scenarios and visualize outcomes, helping them grasp difficult concepts more easily.
- Tutorial Websites: Websites that offer step-by-step guides and explanations on a variety of subjects can be invaluable for learners who need additional support in understanding challenging material.
- Practice Platforms: Platforms that provide quizzes and exercises tailored to individual progress enable students to test their knowledge and track improvement over time.
- Video Resources: Educational videos, whether on platforms like YouTube or specialized learning sites, can provide clear explanations and examples to help learners reinforce their understanding.
Advantages of Using Online Tools
Integrating online tools into study routines offers numerous benefits:
- Flexibility: Online tools are available 24/7, allowing students to learn and review material whenever it is convenient for them.
- Personalized Learning: Many platforms adjust the difficulty level based on the learner’s progress, ensuring that each student receives a customized experience suited to their needs.
- Immediate Feedback: Online exercises often provide instant feedback, allowing learners to understand their mistakes and correct them immediately, which accelerates the learning process.
By incorporating these online resources into your study routine, you can enhance your learning experience, gain a better understanding of challenging topics, and improve your academic performance.
Insights into Graphing and Data Analysis

Graphing and data analysis are essential skills for interpreting patterns, relationships, and trends within numerical information. These techniques allow individuals to visualize complex data in a way that makes it easier to understand and draw conclusions. Whether it’s for academic purposes, business analysis, or scientific research, the ability to analyze and represent data graphically is a valuable tool in making informed decisions.
Understanding Graphs and Their Applications
Graphs are a powerful way to represent data visually, making trends and relationships easier to identify. There are several types of graphs, each suited for different types of data:
- Line Graphs: These are used to show changes over time or continuous data. They are particularly useful for tracking trends and fluctuations.
- Bar Graphs: Ideal for comparing discrete categories or values, bar graphs present data clearly and can highlight differences between variables.
- Pie Charts: Pie charts display parts of a whole, making them effective for showing percentage distributions of a single category.
- Scatter Plots: These graphs help identify correlations between two variables and are commonly used in scientific and statistical research.
Techniques for Analyzing Data
Analyzing data goes beyond simply plotting it on a graph. To gain valuable insights, consider the following techniques:
- Descriptive Statistics: These are used to summarize data through measures like mean, median, and standard deviation, providing a clearer picture of central tendencies and variability.
- Trend Analysis: Identifying patterns and trends in data helps in predicting future outcomes based on historical information.
- Correlation and Regression: These methods are used to understand the relationship between variables and make predictions based on these relationships.
By mastering the art of graphing and data analysis, individuals can better interpret data, make data-driven decisions, and draw meaningful conclusions from complex information.