
The material covered in this part of the course provides a foundation for understanding more complex mathematical principles. Focusing on fundamental operations and problem-solving techniques, it equips learners with the skills needed to tackle more challenging tasks ahead. This section aims to clarify key concepts and give students the confidence to approach similar topics with ease.
By working through the exercises, individuals can develop a deeper understanding of essential mathematical strategies. The included solutions offer step-by-step explanations, ensuring that no part of the process is left unclear. Through consistent practice, learners can expect to strengthen their abilities and prepare for future academic challenges.
Understanding this portion of the material plays a crucial role in achieving proficiency. The ability to apply these methods to real-world situations will not only enhance academic performance but also improve critical thinking and analytical skills.
Algebra Nation Answer Key Overview
This part of the learning system provides comprehensive solutions designed to support students in mastering fundamental concepts. It serves as a guide, offering clear and concise explanations for the exercises, helping learners navigate through complex problems with ease. The purpose is to ensure that every concept is thoroughly understood and applicable to real-world scenarios.
By following the outlined steps and examining each solution in detail, students can identify common mistakes, reinforce their understanding, and build confidence for future challenges. The explanations are tailored to clarify every step of the problem-solving process, ensuring learners do not miss any crucial detail along the way.
| Exercise | Solution Overview |
|---|---|
| Problem 1 | Step-by-step breakdown to solve basic operations. |
| Problem 2 | Detailed explanation of equations and variables. |
| Problem 3 | Visual representation to simplify the calculations. |
| Problem 4 | Key concepts reinforced with practical examples. |
How to Use Section 7 Effectively
Maximizing the value of this part of the learning program requires a strategic approach to problem-solving and concept review. Each exercise offers an opportunity to apply mathematical techniques in a structured manner, allowing students to not only practice but also solidify their understanding. By breaking down the steps and focusing on one problem at a time, learners can gradually build their skills and tackle more complex tasks with confidence.
Approach Each Problem Step by Step
When using this material, it’s essential to follow the provided solutions carefully. Start with the simplest problems and work through the explanations to understand the logic behind each step. By mastering the fundamentals, you’ll be better equipped to handle more difficult challenges.
Reinforce Your Understanding with Practice
Repeated practice of similar problems enhances retention and sharpens critical thinking. After reviewing the provided solutions, attempt to solve related problems on your own. This active approach ensures you develop a deeper understanding and retain the techniques for future use.
| Tip | Explanation |
|---|---|
| Review Solutions | Carefully examine each step of the problem-solving process to understand the rationale behind each decision. |
| Practice Regularly | Consistency is key; regular practice helps reinforce your understanding and increases retention of key concepts. |
| Ask Questions | If certain steps remain unclear, don’t hesitate to ask questions or seek additional resources to clarify the process. |
Key Concepts Covered in Section 7
This part of the learning material focuses on core mathematical principles that serve as the foundation for more advanced topics. It emphasizes a variety of techniques and strategies aimed at helping students improve their problem-solving skills and gain a deeper understanding of fundamental concepts. By mastering these essential ideas, learners will be better prepared for complex tasks and applications in their studies.
The concepts introduced in this section are designed to reinforce and build upon previous knowledge while introducing new methods and strategies. Each topic is carefully explained, ensuring students can grasp the underlying principles and apply them confidently in different situations.
| Concept | Description |
|---|---|
| Basic Operations | Understanding the core operations of addition, subtraction, multiplication, and division and their applications in solving problems. |
| Equations | How to balance and solve different types of equations, including linear and quadratic forms. |
| Variables and Expressions | Understanding the role of variables in mathematical expressions and how to manipulate them to simplify or solve problems. |
| Problem-Solving Strategies | Techniques for breaking down complex problems into manageable steps and solving them efficiently. |
Step-by-Step Solutions for Section 7
This part of the material provides detailed solutions to the exercises, breaking down each problem into manageable steps. The goal is to help students understand the logical flow of solving mathematical problems by showing how to approach each task from start to finish. By following these structured steps, learners can gain confidence in their ability to solve similar problems independently.
Each solution includes a clear explanation of the process involved, ensuring that the steps are easy to follow. Additionally, visual aids or examples may be provided to further clarify complex ideas, making the learning process more intuitive. The breakdown ensures no concept is skipped, and learners can see how each step builds upon the previous one to reach the final solution.
Tips for Mastering Section 7
To successfully navigate this part of the course and truly understand the material, it’s important to approach each task with a focused and strategic mindset. Breaking down complex concepts and practicing regularly will help you retain what you’ve learned and build the confidence needed for more advanced topics. Here are some helpful strategies to ensure your success in mastering this content.
Understand the Core Concepts
- Review the definitions and key principles before starting the exercises.
- Ensure that you fully grasp each step in the solution process.
- Focus on understanding the logic behind each problem, not just the final answer.
Practice Regularly and Consistently
- Start with simpler problems and gradually move to more complex ones.
- Repetition is key to reinforcing the material and improving your problem-solving skills.
- Test your understanding by solving similar problems without referring to the solutions.
By applying these strategies, you’ll be able to approach challenges more confidently and develop a deeper understanding of the material, setting yourself up for future success.
Common Mistakes in Section 7 Exercises
While working through the exercises in this part of the material, students often encounter certain errors that can hinder their progress. These mistakes typically arise from misunderstandings of key concepts, misinterpretations of problem requirements, or simple calculation errors. Identifying these common pitfalls is crucial for improving performance and avoiding frustration. Below are some of the most frequent mistakes to watch out for and tips on how to avoid them.
Misunderstanding the Problem Requirements
- Overlooking important details in the question, such as specific instructions or restrictions.
- Failing to recognize the type of problem being solved, leading to incorrect methods being applied.
- Not reading through the entire problem before attempting a solution, which can lead to missing key information.
Calculation and Simplification Errors
- Incorrectly performing basic operations, such as adding or subtracting negative numbers.
- Making mistakes when simplifying fractions or equations, which can lead to incorrect results.
- Forgetting to check work after solving, which can allow small errors to go unnoticed.
Being aware of these common errors and actively working to avoid them will help improve accuracy and efficiency in solving problems. Take the time to carefully review your work and ensure you understand the underlying principles to minimize these mistakes.
How Section 7 Helps with Algebra Skills
This part of the curriculum is designed to reinforce and build essential mathematical skills that are crucial for more advanced studies. It provides a structured approach to solving problems, breaking down complex concepts into manageable steps. By following the exercises and solutions provided, learners can develop stronger problem-solving abilities, which are essential for mastering more difficult topics in mathematics.
Developing Problem-Solving Strategies
The exercises in this section encourage learners to think critically and develop systematic approaches to solving mathematical problems. By practicing different types of problems, students learn how to recognize patterns, identify key variables, and choose the right methods for finding solutions. These skills are transferable to more complex challenges and real-world applications.
Building Confidence and Fluency
Regular practice with the material helps students become more fluent in performing calculations and solving equations. As learners gain experience, their confidence grows, allowing them to approach even the most challenging problems with greater ease. This consistent practice is key to reinforcing the skills needed for success in future courses and examinations.
Understanding Algebra Nation’s Approach
The learning platform uses a structured method designed to guide students through complex mathematical concepts by breaking them down into digestible steps. This approach emphasizes clarity and mastery, ensuring learners can build a solid foundation before progressing to more challenging material. By integrating theory with practice, the method encourages students to understand the reasoning behind each solution rather than simply memorizing procedures.
Each exercise is crafted to reinforce essential skills, promoting active engagement through a variety of problem types. The goal is to encourage critical thinking, helping students not only arrive at the correct answers but also understand how and why specific methods work. This approach fosters both conceptual understanding and practical application, which are key for long-term success in mathematics.
Importance of Practice in Section 7
Consistent practice is a critical factor in mastering the content of this part of the curriculum. It allows students to reinforce their understanding, sharpen their problem-solving skills, and gain confidence in their abilities. By working through various exercises, learners can familiarize themselves with different types of problems and recognize patterns that will help them solve future challenges more efficiently.
Through regular practice, students develop fluency in applying the concepts they’ve learned, making it easier to tackle more complex problems. The more problems you solve, the more familiar and comfortable the methods become. Here are some reasons why practice is essential for success in this material:
- Builds Confidence: As you solve problems, you gain confidence in your ability to approach similar tasks independently.
- Reinforces Concepts: Repeated exposure to the material helps solidify your understanding and ensures that you retain key concepts over time.
- Improves Speed: The more you practice, the quicker you become at recognizing patterns and applying the correct solutions.
- Identifies Weak Areas: Practice helps pinpoint areas where you may need further review, allowing you to focus your efforts where they’re most needed.
By incorporating regular practice into your study routine, you’ll ensure steady progress and a deeper understanding of the material, setting yourself up for success in future topics.
Section 7 Strategies for Success
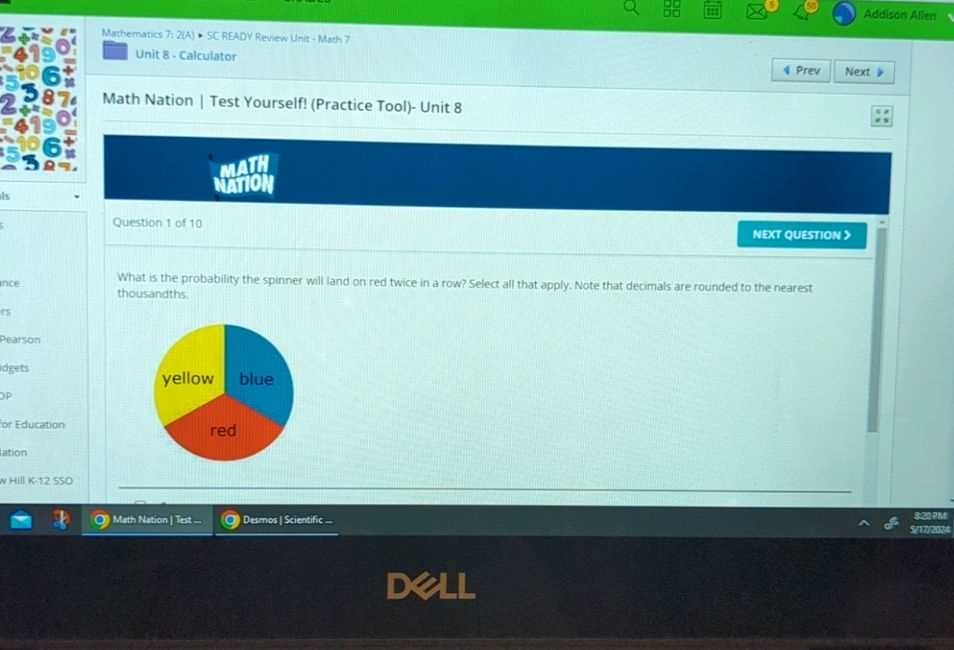
Success in this part of the curriculum requires a combination of effective study techniques, focused attention, and consistent practice. Developing a solid strategy will help you tackle problems with confidence and improve your overall understanding. The following tips will guide you through the most effective approaches to mastering the material and achieving strong results.
One of the most important strategies is breaking down each problem into smaller, manageable steps. This allows you to focus on each part of the solution and ensures you don’t overlook crucial details. Additionally, organizing your study time and setting clear goals for each session will keep you on track and prevent you from feeling overwhelmed.
Another key element to success is reviewing your work regularly. This will help reinforce the concepts you’ve learned and identify any mistakes that may have gone unnoticed during your first attempt. Finally, don’t hesitate to seek help when needed. Whether it’s through online resources, study groups, or asking for clarification from a teacher, reaching out for support can accelerate your understanding and make the learning process more efficient.
Real-Life Applications of Algebra Section 7

The skills and concepts explored in this part of the curriculum have broad applications in the real world. From personal finance to technology, the problem-solving abilities developed in this section are essential for navigating everyday challenges and making informed decisions. Understanding these principles opens up many career and academic paths, allowing you to apply your knowledge in various professional settings.
Personal Finance and Budgeting
One of the most practical uses of the concepts learned here is in managing personal finances. Whether you’re calculating expenses, planning a budget, or evaluating loan interest rates, the ability to manipulate variables and solve equations can help you make smarter financial choices. Mastering these methods can enable you to understand how your income, savings, and expenditures relate to one another and ensure that you stay on top of your financial goals.
Technology and Engineering Fields
In fields like technology and engineering, the principles explored in this section play a crucial role in problem-solving. Engineers use mathematical models to design structures, analyze data, and optimize systems. Understanding these concepts is key to working with algorithms, software development, and systems analysis, where accuracy and precision are vital.
What Students Struggle With in Section 7

While this part of the curriculum offers valuable learning opportunities, students often face challenges as they work through the material. Common struggles typically stem from misunderstanding core concepts, difficulty applying learned techniques, or rushing through problems without proper attention to detail. Recognizing these challenges early on can help learners focus on overcoming them effectively.
One of the main issues students encounter is the misapplication of mathematical operations. In many cases, learners may forget to follow the correct order of operations or misinterpret the problem’s structure, leading to incorrect solutions. To overcome this, it’s essential to practice step-by-step problem solving and review previous exercises for better comprehension.
Another area of difficulty involves abstract reasoning and variables. Many students struggle to connect variables with real-world situations, making it harder to understand the relationships between different quantities. Strengthening this conceptual understanding requires additional practice and examples that show how mathematical concepts apply outside of the classroom.
How Section 7 Prepares for Advanced Topics
This portion of the curriculum serves as a foundational building block for more complex mathematical concepts. By mastering the skills and techniques covered here, students develop critical thinking abilities and problem-solving strategies that are essential for tackling more advanced topics. The concepts introduced in this section are designed to create a smooth transition to higher-level subjects, making them easier to grasp and apply in future studies.
Here are some ways in which this section helps prepare students for more challenging material:
- Strengthening Core Problem-Solving Skills: Understanding basic mathematical principles lays the groundwork for approaching complex equations and problems in higher-level coursework.
- Introducing Variable Manipulation: Handling variables and understanding their relationships is a key skill required in advanced topics like calculus and higher-order algebra.
- Establishing Logical Thinking Patterns: By working through problems systematically, students begin to develop the logical frameworks needed for abstract topics in mathematics.
In summary, the lessons learned here are not only important for success in the current material but also for future academic endeavors. Mastery of this content ensures a smoother progression into more advanced subjects in the field.
Reviewing Key Problems in Section 7
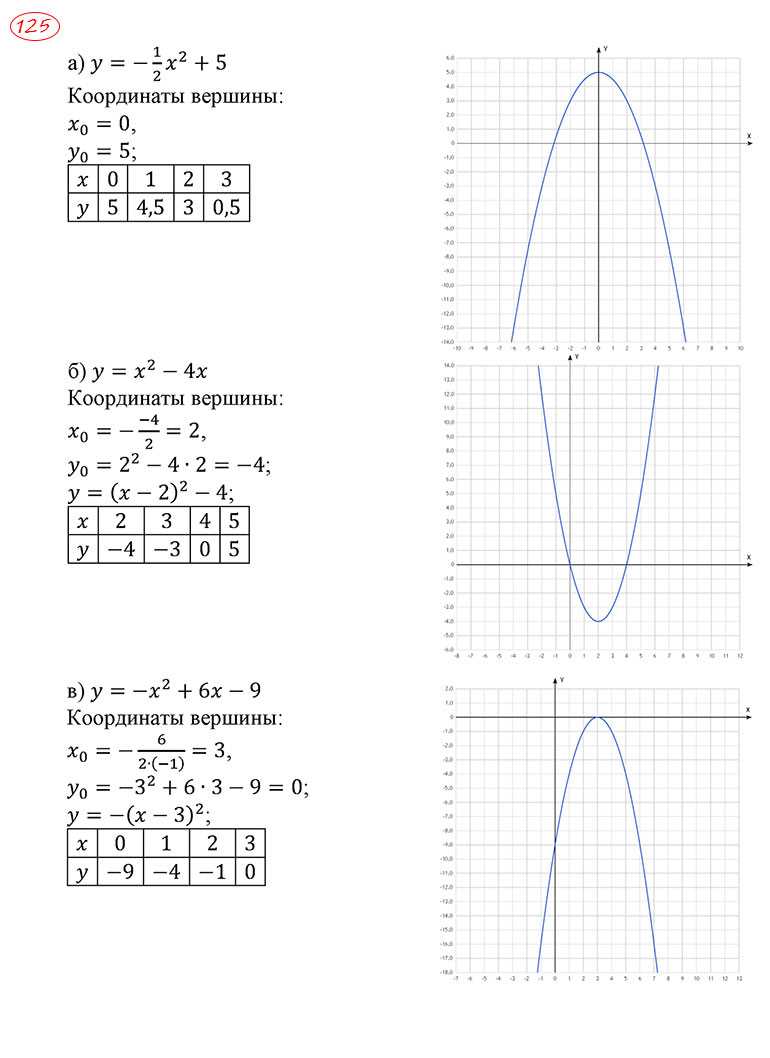
Revisiting critical exercises is an effective approach to reinforcing concepts and improving problem-solving skills. By focusing on the most important types of problems, learners can ensure a stronger grasp of fundamental principles. A focused review of challenging questions helps solidify knowledge, correct misconceptions, and boosts confidence when moving on to more complex material.
Commonly Encountered Problems
While working through various types of problems, some tend to be more difficult than others. Identifying these and dedicating more time to them can be highly beneficial. The following table provides examples of common exercises that often require additional practice:
| Problem | Solution |
|---|---|
| Solve for x: 5x – 3 = 17 | x = 4 |
| What is the area of a triangle with a base of 8 units and height of 6 units? | Area = 24 square units |
| Simplify: 3(2y + 5) = 24 | y = 3 |
Approach to Problem Solving
When revisiting these problems, it’s helpful to break them down step-by-step. Start by carefully reading the problem and identifying known values and what is being asked. Then, apply the relevant methods to solve the problem, checking each step along the way. By repeating this process, students become more adept at recognizing patterns and efficiently applying strategies to similar problems.
Section 7 and Test Preparation
Mastering the material presented in this part of the course is essential for effective preparation for exams. By engaging with the exercises and understanding the underlying concepts, students can build a solid foundation to confidently tackle more advanced problems. Focused practice and repetition allow learners to not only recall key methods but also improve their problem-solving speed and accuracy.
Building Confidence through Practice
Frequent practice with a range of problems is the most effective way to ensure readiness. Regularly revisiting concepts and attempting different types of questions helps cement the material in memory. Consistent effort over time reduces anxiety, as students feel increasingly comfortable with the process and recognize familiar patterns in new problems.
Test-Taking Strategies
Along with mastering the material, employing effective strategies during the exam is crucial. Some tips for success include:
- Time management: Allocate specific time for each question and move on if a problem takes too long to solve.
- Reading carefully: Ensure all details are understood before beginning to solve.
- Checking work: Always double-check calculations to avoid simple mistakes.
Preparation is key, but remaining calm and focused during the exam can make all the difference in achieving success.
How to Track Progress in Section 7
Monitoring progress is essential for understanding how well you are grasping the material and identifying areas that need more attention. By regularly assessing your performance, you can make adjustments to your study habits, focus on challenging topics, and stay motivated. Tracking progress not only helps gauge your current level of understanding but also keeps you on track toward mastering the content.
Effective Ways to Monitor Your Progress
There are several strategies you can use to track your development as you move through the exercises and problems in this part of the course:
- Review past performance: Look back at previous exercises and quizzes to identify areas where mistakes were made or where concepts weren’t fully understood. Revisit these topics to reinforce your knowledge.
- Set measurable goals: Break down larger topics into smaller, achievable goals. For example, aim to complete a certain number of practice problems or master a particular concept each week.
- Use self-assessment tools: Many learning platforms offer quizzes or self-assessments that can help evaluate your understanding. Take these regularly to check your progress and highlight any weak spots.
Tracking Progress with Consistency
Consistency is key to seeing improvement over time. By setting aside dedicated time for review and practice, you can maintain steady progress. Consider using a progress tracker or journal to note your achievements and any challenges you face. This will provide a clear visual representation of your growth and motivate you to keep moving forward.
- Daily check-ins: Take a few minutes each day to reflect on what you’ve learned and what you still need to work on.
- Weekly reviews: At the end of each week, assess your overall progress and adjust your study plan if needed.
By tracking your progress consistently, you’ll gain a deeper understanding of your strengths and areas for improvement, allowing you to stay on track toward success.
Resources for Further Learning in Section 7
To deepen your understanding and improve your skills, exploring additional resources can be highly beneficial. Whether you’re looking to reinforce your knowledge, tackle more complex problems, or explore different learning formats, there are various tools available to help you progress. By engaging with supplementary materials, you can strengthen your grasp of the topics and stay motivated as you work through more challenging concepts.
Online Platforms and Tutorials
Numerous websites and educational platforms offer comprehensive tutorials and practice problems that complement what you’re learning. These can provide step-by-step explanations, interactive exercises, and real-time feedback, making them valuable for students at all levels.
- Interactive learning platforms: Websites like Khan Academy, Coursera, and edX offer video tutorials and exercises on a wide range of related topics.
- Educational YouTube channels: Channels dedicated to specific math topics can be helpful for visual learners, breaking down complex ideas into easy-to-understand segments.
- Online forums and discussion boards: Joining communities like Stack Exchange or Reddit can give you access to peer support and additional explanations from fellow learners and instructors.
Books and Printed Resources
For students who prefer learning through reading, books can provide in-depth explanations and additional examples. Many textbooks and workbooks are available that cover essential concepts and offer practice questions for mastering the material.
- Workbooks: These often contain a variety of problems, ranging from basic to advanced, that allow students to practice applying what they’ve learned.
- Study guides: Compact study guides break down key concepts and offer concise explanations, making them ideal for quick reference or review.
- Practice problem books: These resources offer thousands of problems with detailed solutions, helping you identify patterns and improve problem-solving techniques.
Exploring a combination of these resources will allow you to approach the material from multiple angles, enhancing your overall learning experience and ensuring long-term success. By dedicating time to using these additional tools, you’ll be better prepared to tackle more advanced topics in the future.