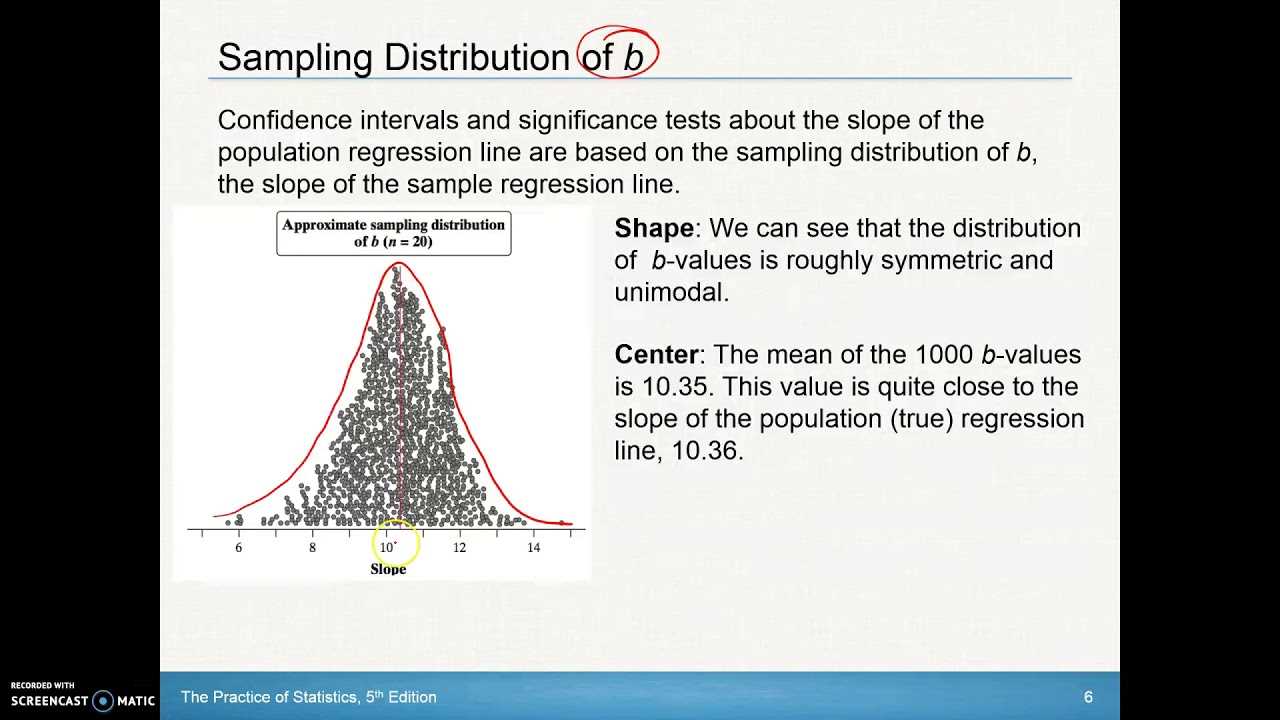
The concepts explored in this section play a crucial role in developing a deeper understanding of data analysis and interpretation. The problems presented challenge your ability to apply various techniques effectively and interpret results accurately. Mastery of these methods is essential for success in both academic assessments and real-life applications.
In this guide, we will provide detailed solutions to help you navigate through complex questions. By reviewing each solution, you will gain valuable insights into common approaches and best practices, allowing you to improve your problem-solving skills. This resource is designed to support your learning journey and enhance your comprehension of key ideas.
Reviewing the material thoroughly will allow you to identify patterns and refine your techniques. As you progress, you will build confidence in tackling similar problems and applying your knowledge to new challenges. Keep in mind that consistency and practice are the keys to mastering these critical concepts.
AP Statistics Chapter 12 Test Answer Key
This section focuses on reviewing and solving the problems found in one of the most challenging areas of the course. It is designed to help you understand how to approach each problem, apply the appropriate methods, and interpret the results correctly. By examining detailed solutions, you will better grasp the key concepts and improve your ability to solve similar challenges in the future.
Breaking Down the Problems
Each problem in this section tests a specific aspect of data analysis and mathematical reasoning. The questions range from basic applications to more complex scenarios that require careful analysis. Understanding the logic behind each step is essential for success, as it not only prepares you for assessments but also strengthens your analytical skills.
Solution Breakdown
Here, we provide a structured breakdown of how to solve each problem. The following table outlines the methods used to arrive at the correct solutions and highlights common pitfalls to avoid.
| Problem | Solution Approach | Key Considerations |
|---|---|---|
| Problem 1 | Identify variables and apply the formula | Ensure correct interpretation of data |
| Problem 2 | Analyze the graph and extract necessary values | Pay attention to units and scaling |
| Problem 3 | Use appropriate statistical method for hypothesis testing | Check for outliers that may affect results |
Overview of Chapter 12 Concepts
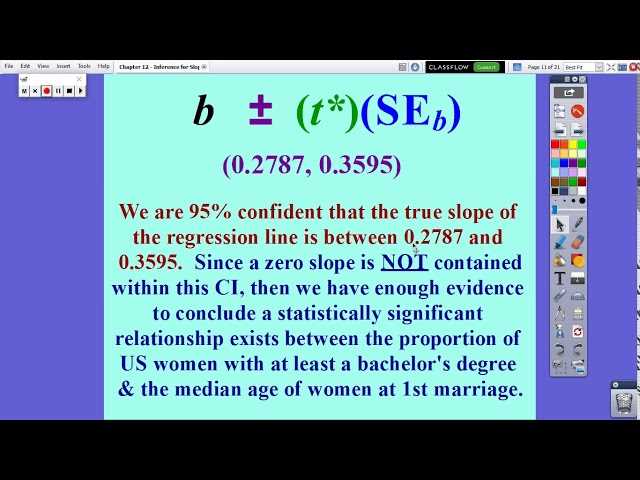
This section focuses on essential concepts that are fundamental to understanding complex data analysis. The methods explored here are designed to help students develop a deeper comprehension of the key ideas and tools needed for solving problems effectively. Mastery of these concepts is crucial for applying them in both academic and practical settings.
Core Principles
The core principles in this section revolve around analyzing sets of data, recognizing patterns, and drawing conclusions based on mathematical reasoning. These ideas serve as the foundation for more advanced topics and are essential for developing the skills necessary to tackle more complex questions. Key areas include:
- Understanding distributions and their properties
- Identifying relationships between variables
- Applying various techniques for hypothesis testing
- Interpreting and visualizing data using charts and graphs
Practical Applications

While the theoretical understanding of these concepts is important, it is equally crucial to apply them to real-world situations. Here are some practical applications that demonstrate the relevance of these ideas:
- Assessing the impact of a new product on consumer behavior
- Evaluating the effectiveness of a marketing campaign
- Determining the reliability of medical testing methods
Understanding Key Statistical Methods
This section delves into the essential techniques that are used to analyze and interpret data. Mastering these methods is critical for drawing accurate conclusions and making informed decisions based on quantitative information. These approaches form the foundation for solving a wide variety of problems that involve data analysis, from basic calculations to more complex evaluations.
Important Techniques and Approaches
Several methods are commonly employed to analyze and summarize data effectively. Understanding when and how to apply each technique is key to accurate interpretation. Below are the main approaches covered in this section:
- Descriptive methods for summarizing data
- Inferential techniques for drawing conclusions from samples
- Methods for testing hypotheses and determining significance
- Tools for measuring variability and spread
Comparison of Key Techniques
To better understand these methods, it’s useful to compare how they differ in terms of application and purpose. The table below outlines some of the most commonly used approaches and their key characteristics:
| Method | Purpose | Typical Use |
|---|---|---|
| Mean and Median | Measure central tendency | Summarize data sets for overall trends |
| Standard Deviation | Measure data variability | Understand spread or consistency in data |
| Regression Analysis | Determine relationships between variables | Predict outcomes based on independent factors |
| Chi-Square Test | Test associations between categorical variables | Assess independence or goodness of fit |
Test Structure and Question Types
This section provides an overview of how assessments in this area are organized and what types of questions you can expect. Understanding the layout and format of the evaluation will help you approach each section with confidence. The structure is designed to assess both theoretical knowledge and practical application of methods.
Types of Questions
The questions in these evaluations generally fall into a few distinct categories, each testing a specific skill or concept. Here are the most common types you’ll encounter:
- Multiple Choice: These questions test your ability to recognize correct answers among several options. They often focus on identifying trends or applying methods to simple problems.
- Short Answer: These questions require you to demonstrate your reasoning and explain your thought process in solving a problem.
- Problem-Solving: These involve more complex scenarios where you need to apply several concepts in a logical sequence to find the correct solution.
- Data Interpretation: In these questions, you are given a set of data and must extract relevant information to draw conclusions or make predictions.
Overall Structure
The layout of the evaluation typically follows a pattern that balances question difficulty across sections. The format is designed to test both your ability to recall key concepts and your proficiency in applying them in various contexts. Here is an overview of how it might be structured:
- Introduction: A few general questions that test basic understanding of core principles.
- Intermediate Questions: A mix of problem-solving and data analysis questions that require deeper application of learned techniques.
- Advanced Problems: More complex scenarios requiring the integration of multiple methods and concepts.
How to Approach AP Statistics Tests
When preparing for assessments in this field, it’s essential to develop a strategy that allows you to manage time effectively and approach each problem with confidence. A well-structured plan not only helps in organizing your thoughts but also ensures that you tackle questions methodically, maximizing your chances for success. Below are some key strategies to keep in mind when facing evaluations.
First, it’s important to read through the entire problem carefully before jumping into calculations. This gives you a clear understanding of what is being asked and helps you identify any key details that might be overlooked in haste. Take your time to analyze the data provided and make sure you grasp the context of each question.
Next, break the question down into smaller, manageable parts. Often, complex problems can be solved step by step by isolating variables or focusing on one aspect of the problem at a time. This method reduces the risk of making errors and helps keep your approach organized.
Finally, don’t forget to check your work. If time allows, review your calculations and reasoning to ensure you’ve answered each part accurately. It’s easy to overlook small mistakes under time pressure, so a quick check can make a significant difference in the final result.
Detailed Solutions to Test Questions
In this section, we provide comprehensive solutions to help you fully understand the steps involved in solving each problem. By breaking down each question into manageable steps, you will gain a clearer understanding of the methods used and the reasoning behind each solution. This approach will also help you recognize common strategies that can be applied to similar problems in the future.
Step-by-Step Breakdown

Each solution is presented with a detailed breakdown of the steps taken to arrive at the final result. By following these steps, you will not only find the correct answer but also understand the underlying concepts. The process of solving problems in this way will help reinforce key ideas and improve your problem-solving skills.
Example Problem
Let’s take a look at an example problem and walk through the solution process:
Problem: Given a data set, calculate the mean and standard deviation, and then determine the margin of error for a confidence interval.
Solution:
- First, calculate the mean by summing all data points and dividing by the number of points.
- Next, compute the variance by determining the squared differences from the mean for each data point, then averaging those differences.
- Take the square root of the variance to find the standard deviation.
- For the margin of error, multiply the standard deviation by the appropriate z-score corresponding to the confidence level.
- Finally, apply this to determine the confidence interval around the mean.
By following these steps, you will arrive at the correct margin of error and interval, and gain a deeper understanding of how to approach similar questions in the future.
Common Mistakes to Avoid in Statistics
When solving problems in this field, it’s easy to fall into certain traps that can lead to incorrect conclusions. Recognizing these common errors and learning how to avoid them can make a significant difference in your results. By being aware of the pitfalls, you can ensure that your approach is sound and that your solutions are accurate.
One common mistake is misinterpreting data or overlooking important details. For example, confusing correlation with causation can lead to false assumptions about the relationships between variables. It’s crucial to carefully analyze the context and data before drawing conclusions.
Another frequent error is neglecting to check calculations, particularly in complex problems involving multiple steps. Small arithmetic mistakes can snowball and result in significantly wrong answers. Taking a moment to double-check each step of your work can help catch these errors early.
Additionally, failing to understand the underlying assumptions of a method or test can lead to improper application of techniques. It’s essential to be clear on the conditions under which each method is valid and to ensure you’re using the right tool for the specific problem at hand.
Strategies for Efficient Test Preparation
Effective preparation is essential for performing well on assessments in this area. Developing a structured approach not only helps retain key concepts but also ensures you can apply them with ease when faced with challenging questions. By using the right techniques and managing your time effectively, you can maximize your study efforts and boost your confidence.
One crucial strategy is to break your study sessions into manageable chunks. Rather than cramming all the material at once, focus on specific topics or techniques during each study session. This approach allows for deeper understanding and helps reduce the feeling of being overwhelmed.
Another helpful tactic is to practice with sample problems. Actively working through various types of problems familiarizes you with the question formats and reinforces key concepts. Be sure to time yourself during practice sessions to simulate actual exam conditions and improve your ability to work efficiently under pressure.
Finally, review and summarize the most important concepts regularly. Rather than passively rereading notes, try teaching the material to someone else or creating summary sheets with the main points. This method reinforces learning and helps identify any areas that may need further attention before the exam.
Analyzing Data with Confidence
When working with data, confidence in your analysis is crucial. Understanding how to interpret and draw conclusions from data sets allows you to make informed decisions and effectively communicate results. By following structured approaches and using appropriate methods, you can tackle even the most complex data confidently.
The first step in analyzing data is to ensure that you understand the context. Knowing what each piece of information represents and what the overall goal of the analysis is will guide you in selecting the right techniques. Confidence comes from clarity, and understanding the purpose of your analysis makes the process more straightforward.
Steps to Confident Analysis
To ensure that you approach data analysis with confidence, follow these key steps:
- Organize the data: Start by ensuring the data is clean and properly structured. This makes it easier to identify trends and potential outliers.
- Visualize the data: Use graphs or charts to represent the data. Visualization can reveal patterns and relationships that might not be obvious from the raw numbers alone.
- Apply appropriate methods: Use statistical techniques or other analytical methods that fit the data type and problem you are addressing. This could involve calculating averages, determining correlations, or running more advanced analyses.
- Draw conclusions: Based on your analysis, draw meaningful conclusions. Make sure your findings are backed by the data and aligned with the objectives of the analysis.
Building Confidence in Your Results
Building confidence also involves reviewing your findings critically. Double-check your work and assess the reliability of your results. Are there alternative interpretations? Do the data support your conclusions under different conditions? Confidence in your results comes from being thorough and ensuring the analysis is both valid and relevant.
Critical Thinking in Statistical Problems
When solving problems involving data analysis, critical thinking is essential for ensuring that your conclusions are both valid and meaningful. It involves not only performing the necessary calculations but also understanding the underlying assumptions, recognizing biases, and considering alternative interpretations. Approaching problems with a critical mindset ensures that you are drawing conclusions based on solid reasoning, not just numbers.
A key aspect of critical thinking is questioning the data itself. Are the numbers reliable? Were they collected in a way that is representative of the population or situation you’re analyzing? Taking the time to evaluate the quality of the data can help you avoid jumping to conclusions based on faulty or incomplete information.
Another important factor is interpreting the results within the appropriate context. Data can tell many different stories, and it is your job to determine the most plausible explanation based on the evidence available. This requires careful consideration of the problem at hand, the methods used to collect the data, and the potential impact of any confounding factors.
Critical thinking also involves being mindful of potential cognitive biases. Confirmation bias, for example, may cause you to seek out evidence that supports your preconceived ideas, while ignoring or undervaluing evidence that contradicts your position. To avoid such pitfalls, always strive to look at the problem from multiple angles and be open to adjusting your conclusions based on new information.
Time Management Tips for the Test

Effective time management is essential for performing well in any assessment. By learning how to prioritize tasks, allocate time efficiently, and stay focused under pressure, you can maximize your chances of success. This section offers practical tips on how to organize your approach to ensure that you can complete each section within the allotted time, without sacrificing accuracy.
Strategies for Efficient Time Use
To manage your time effectively, it’s important to have a clear plan before you begin. Here are some strategies to help:
- Read instructions carefully: Start by reading all instructions thoroughly. Understanding the requirements of each question will prevent unnecessary mistakes that waste time.
- Divide your time: Break the overall time into smaller blocks for each section. For example, if the test consists of multiple sections, allocate a specific amount of time for each one based on its complexity.
- Start with easier questions: Begin with questions that seem the easiest to answer. This will help build your confidence and leave more time for the challenging ones later.
- Keep track of time: Use a watch or the provided timer to monitor how much time is left. If you’re running out of time, move on to the next section and return to unfinished questions later if possible.
- Don’t dwell on difficult questions: If you encounter a challenging question, don’t spend too long trying to solve it. Move on and come back to it later when you’ve completed the easier ones.
Time Management During Practice

It’s also important to practice time management during your study sessions. By simulating test conditions at home, you can develop a better understanding of how to pace yourself. Time yourself while working through practice problems or sample exams, and aim to improve both your speed and accuracy over time.
| Strategy | Benefit |
|---|---|
| Start with easy questions | Builds confidence and saves time for harder questions |
| Set time limits per section | Ensures that all areas of the test are covered |
| Keep track of time during practice | Improves speed and familiarizes with pacing |
Key Formulas for Chapter 12
Understanding and applying mathematical formulas is essential when analyzing data and making inferences. In this section, we’ll review some of the most important equations that you need to remember for success in this area. These formulas form the foundation for solving various types of problems and provide the necessary tools to interpret and manipulate data efficiently.
Essential Equations for Data Analysis
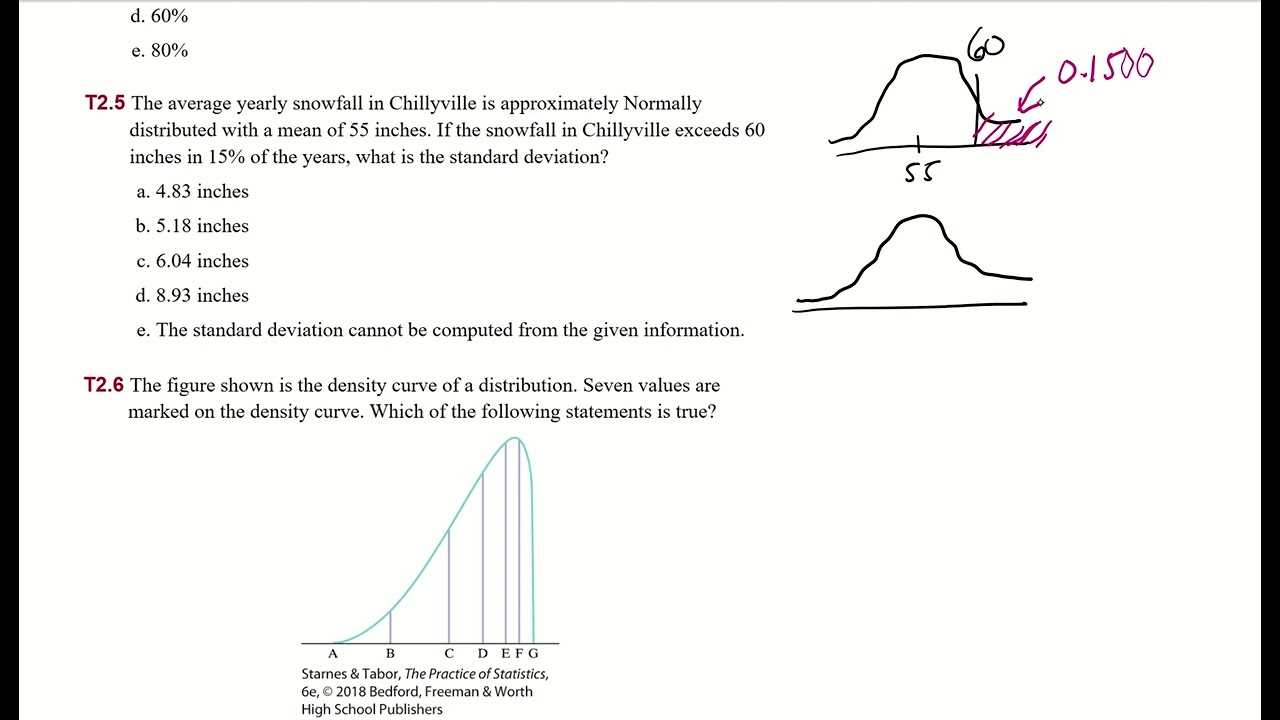
Several formulas are frequently used to summarize data, calculate probabilities, and assess relationships between variables. Below are some of the key equations that you should familiarize yourself with:
- Mean of a Distribution: The mean is the sum of all values divided by the total number of values. This formula helps summarize a set of data points.
- Standard Deviation: The standard deviation is a measure of how spread out the values are in a dataset. It is calculated as the square root of the variance.
- Variance: Variance is the average of the squared differences from the mean. It provides insight into the dispersion of data points.
- Z-Score: Z = (X – μ) / σ. This formula standardizes a value, allowing comparison across different datasets or distributions.
- Linear Regression Equation: y = mx + b. This equation is used to model the relationship between two variables, where m represents the slope and b represents the y-intercept.
Formulas for Hypothesis Testing and Confidence Intervals
In addition to the basic measures of central tendency and dispersion, understanding formulas for hypothesis testing and constructing confidence intervals is crucial. Here are some of the most commonly used equations:
- Confidence Interval for a Mean: CI = x̄ ± (z* × (σ/√n)), where x̄ is the sample mean, z* is the z-value for the desired confidence level, σ is the population standard deviation, and n is the sample size.
- Hypothesis Test for a Mean: t = (x̄ – μ) / (s / √n), where x̄ is the sample mean, μ is the population mean, s is the sample standard deviation, and n is the sample size.
- Chi-Square Test: χ² = Σ((O – E)² / E), where O is the observed frequency and E is the expected frequency. This test is used for categorical data analysis.
Interpreting Graphs and Data
Interpreting visual representations of data is a crucial skill in any analytical task. Graphs, charts, and plots provide an intuitive way to observe trends, relationships, and distributions. By understanding how to read and analyze these visuals, you can draw meaningful conclusions and make informed decisions based on data.
Types of Graphs and Their Uses

Different types of graphs serve distinct purposes when presenting data. Understanding which graph to use in a given scenario and how to interpret it is key to extracting valuable insights.
- Bar Graphs: Useful for comparing discrete categories or groups. The length of each bar represents the value or frequency of the category.
- Histograms: Display the distribution of numerical data, showing the frequency of data within certain intervals or ranges.
- Box Plots: Represent data distribution through quartiles, highlighting the median, interquartile range, and outliers.
- Scatter Plots: Show the relationship between two continuous variables. Points on the plot represent pairs of values.
Key Elements to Focus On
When interpreting graphs, it’s essential to focus on certain elements to accurately understand the data they represent. These include:
- Scale: Always check the scale on the axes, as this affects how the data is represented and can influence interpretation.
- Trends: Look for general patterns in the data, such as increasing or decreasing trends, which can help in making predictions or conclusions.
- Outliers: Identifying outliers or extreme values is critical as they can significantly affect the analysis and conclusions drawn from the data.
- Clusters: Groups of data points that appear together can indicate meaningful relationships or categories within the dataset.
Example: Interpreting a Data Set
The table below represents a simple dataset of sales figures for different products over a period of time:
| Product | Sales (Units) | Month |
|---|---|---|
| Product A | 250 | January |
| Product B | 350 | January |
| Product A | 300 | February |
| Product B | 450 | February |
In this table, Product B shows an increasing trend in sales over the two months, while Product A has a slight increase as well. By graphing these sales figures, one could quickly spot the trends and draw conclusions about product performance.
Real-World Applications of Data Analysis
Data analysis plays a critical role in a wide range of industries, helping professionals make informed decisions, optimize processes, and improve outcomes. By examining data patterns, businesses and organizations can gain insights that drive strategies, improve efficiency, and foster innovation. The ability to apply analytical methods to real-world situations is essential for solving complex problems across various fields.
Business and Marketing

In the world of business, data analysis is used to understand customer preferences, predict trends, and enhance decision-making. Key areas where this is applied include:
- Customer Segmentation: Analyzing purchasing behavior to group customers into segments for targeted marketing.
- Market Research: Using surveys and feedback to gauge customer satisfaction and improve products or services.
- Sales Forecasting: Predicting future sales trends by analyzing past performance and market conditions.
- Price Optimization: Analyzing price elasticity and demand to set optimal pricing strategies for products or services.
Healthcare and Medicine

In healthcare, data analysis is fundamental for improving patient outcomes, advancing research, and optimizing healthcare services:
- Predictive Modeling: Forecasting disease outbreaks or patient health risks using historical data.
- Clinical Trials: Analyzing the effectiveness of medical treatments and interventions through controlled experiments.
- Healthcare Operations: Improving patient care efficiency and reducing wait times through data-driven management decisions.
- Personalized Medicine: Using patient data to tailor treatment plans based on individual genetic profiles.
Government and Public Policy

Governments and policymakers rely on data to guide decision-making and shape policies that affect public welfare:
- Census Data: Collecting and analyzing demographic information to allocate resources and design public programs.
- Economic Planning: Assessing economic trends to make decisions on fiscal policies, taxation, and public spending.
- Public Health: Tracking and controlling the spread of diseases through statistical modeling and surveillance systems.
From predicting consumer behavior to shaping policies that affect millions, the real-world applications of data analysis are vast and essential. By using analytical methods, professionals can transform raw data into actionable insights that drive innovation and improve outcomes across various sectors.
Using the Answer Key for Self-Review
Self-assessment is a crucial part of the learning process, allowing students to evaluate their understanding and identify areas that need improvement. Utilizing solutions guides effectively can help reinforce key concepts and improve performance in future assessments. By reviewing both correct and incorrect responses, learners can gain a deeper understanding of the material and refine their problem-solving skills.
How to Maximize Your Self-Review
When using a solution guide to review your work, it’s important to approach it methodically:
- Review Mistakes: Carefully analyze where you went wrong and understand why the correct answer is different. Identify any patterns in your mistakes, such as misinterpreting questions or making calculation errors.
- Understand the Method: Focus on the techniques used to solve each problem. Understand the step-by-step reasoning behind the solution, as it can help you apply the same methods to similar problems in the future.
- Verify Your Understanding: Once you’ve reviewed your mistakes, try solving similar questions without looking at the solutions to ensure you’ve grasped the concept.
- Take Notes: Write down any important formulas or concepts that you struggled with. This will help reinforce your learning and serve as a reference for future practice.
Benefits of Self-Review
Using a solutions guide for self-assessment has several advantages that can accelerate your learning process:
- Boosts Confidence: By identifying and correcting mistakes, you’ll feel more confident in your ability to handle similar problems on your own.
- Enhances Understanding: Breaking down each solution helps you understand the concepts more thoroughly, which can improve your retention and application of knowledge.
- Identifies Gaps in Knowledge: Reviewing the solutions allows you to pinpoint areas where you may still have weaknesses, providing a targeted focus for further study.
Self-review, when done properly, can significantly enhance your grasp of the subject. By incorporating these practices, you will not only improve your performance but also build a deeper understanding that will serve you well in future assessments and real-world applications.
Test-Taking Tips for Success
Approaching any assessment with a clear strategy can greatly impact your performance. Effective test-taking involves not only understanding the material but also managing your time, minimizing stress, and using smart tactics to navigate through different types of questions. By applying a few key techniques, you can optimize your chances of success and approach the assessment with confidence.
Time Management Strategies
Managing your time wisely during an assessment is crucial. Here are some tips to stay on track:
- Read Instructions Carefully: Before starting, ensure you fully understand the requirements of the exam. This will help you avoid mistakes and unnecessary time spent on misinterpreted questions.
- Budget Your Time: Allocate a specific amount of time for each section of the assessment. Keep an eye on the clock to avoid spending too much time on any one part, which can leave you rushed at the end.
- Prioritize Easy Questions: Start with the questions you find easiest. This will help build momentum and boost your confidence early on.
Strategies for Answering Questions
When tackling different types of questions, approach them with a clear strategy:
- Process of Elimination: For multiple-choice questions, eliminate obviously incorrect answers first. This increases your chances of selecting the correct option even if you’re unsure.
- Stay Calm with Difficult Questions: If you come across a challenging question, don’t panic. Skip it and come back later after you’ve completed the rest of the exam. Often, a fresh perspective can help you find the right answer.
- Write Clearly: For open-ended questions, make sure your answers are well-structured and easy to follow. If your reasoning is clear, partial credit is more likely.
Mindset and Focus
Your mindset plays a big role in your performance. Consider these tips for maintaining focus:
- Stay Positive: Keep a positive attitude throughout the assessment. Confidence can improve your clarity of thought and decision-making.
- Practice Mindfulness: Take a deep breath if you start feeling overwhelmed. Mindfulness techniques, such as focusing on your breathing, can help calm your nerves and bring you back to a place of focus.
- Double-Check Your Work: If time permits, review your answers before submitting. This will give you a chance to catch any mistakes or revise any unclear responses.
By applying these strategies, you’ll approach your assessments more effectively, increasing your chances of success. Remember that preparation, time management, and a positive mindset are key components for performing well under pressure.
Additional Resources for AP Statistics
For students looking to deepen their understanding or seek additional support, there are many valuable resources available. These materials can help reinforce concepts, provide extra practice, and offer explanations from different perspectives. Whether you’re looking for textbooks, online platforms, or study groups, utilizing these resources can significantly enhance your preparation and understanding.
Online Platforms and Websites
There are numerous online resources that offer interactive tools, video lessons, and practice exercises. Some popular options include:
- Khan Academy: Offers free video tutorials covering a wide range of topics with practice exercises for reinforcement.
- Coursera: Features courses from universities and institutions that dive deeper into relevant concepts, often with assessments to test your knowledge.
- Quizlet: Allows students to create flashcards and quizzes for efficient memorization of key concepts and formulas.
Books and Textbooks
Books remain a reliable and comprehensive method of learning. These texts not only provide theoretical knowledge but also include practice problems and real-world applications:
- The Practice of Research in Social Sciences: This textbook offers detailed discussions on experimental designs and analysis methods, essential for mastering the subject.
- Five Steps to a 5: A popular study guide that covers all the key concepts and practice problems designed specifically for the exam.
- AP Exam Review Books: Many publishing houses provide specialized AP exam prep books with full-length practice tests, answering strategies, and detailed explanations.
Study Groups and Forums
Collaborating with peers and engaging in study groups can improve your grasp on difficult topics. Consider joining online forums and discussion groups where students exchange knowledge and solve problems together:
- Reddit AP Subreddits: Communities like r/APStatistics offer advice, problem-solving tips, and shared resources for exam preparation.
- Discord Study Servers: Many Discord servers are dedicated to helping students by providing a platform to discuss difficult topics and collaborate on practice problems.
By leveraging a combination of online resources, books, and peer discussions, students can build a deeper understanding and improve their chances of success. Remember, consistency and variety in learning methods are key to mastering the subject.
Improving Your Statistical Skills
Enhancing your ability to analyze data and solve related problems involves consistent practice and a structured approach to understanding core concepts. By focusing on critical thinking, methodical problem-solving, and real-world applications, you can sharpen your skills and gain confidence in applying these techniques. The process requires a balance of theoretical knowledge and practical experience, both of which can be developed through various methods and resources.
Building a Strong Foundation
Before diving into complex problems, it is important to ensure a strong grasp of the foundational concepts. Here are some effective ways to reinforce the basics:
- Review Core Concepts: Regularly revisit key ideas such as measures of central tendency, data distributions, and hypothesis testing. Mastering these fundamentals is crucial for solving more advanced problems.
- Work Through Examples: Practice solving example problems from textbooks or online resources. Pay attention to the methodology used in the solutions and how the steps are logically connected.
- Use Visual Aids: Graphs, charts, and other visual tools help to better understand relationships in data and support the process of drawing conclusions based on numerical analysis.
Practical Application of Techniques
Applying learned methods to real-life data is an essential step in developing proficiency. Here are some tips for gaining practical experience:
- Work on Data Sets: Start with simple datasets and gradually move to more complex ones. Try to interpret trends, correlations, and distributions.
- Participate in Online Challenges: Many websites and platforms offer data analysis challenges where you can apply what you’ve learned in a competitive setting. This provides valuable practice under timed conditions.
- Collaborate with Others: Join study groups or online forums where you can discuss problems and solutions with others. Collaborative learning helps to uncover new approaches and solidify your understanding.
By combining theoretical learning with hands-on practice, you can significantly improve your analytical skills and better prepare yourself for challenges in the field. Continuously challenging yourself with new problems and seeking feedback will help you stay on track toward mastering the subject.