AP Statistics Test 4C Answer Key Detailed Solutions

In this section, we delve into the solutions and approaches for a set of challenging academic exercises that test your grasp of key concepts. These problems require a solid understanding of various analytical techniques, offering a chance to apply theoretical knowledge to real-world scenarios.

Mastering problem-solving strategies is essential for excelling in this kind of examination. Each question tests a different skill set, ranging from data interpretation to probability calculations. With step-by-step explanations, we aim to provide clarity and guide you through the most effective methods for tackling these tasks.

Throughout the guide, we focus on breaking down each problem into manageable steps. This approach will help build confidence and ensure that all aspects of the challenge are addressed thoroughly. Whether you’re preparing for an upcoming evaluation or simply looking to improve your understanding, this resource is designed to be a valuable tool for your academic journey.

Understanding the AP Statistics Test Structure

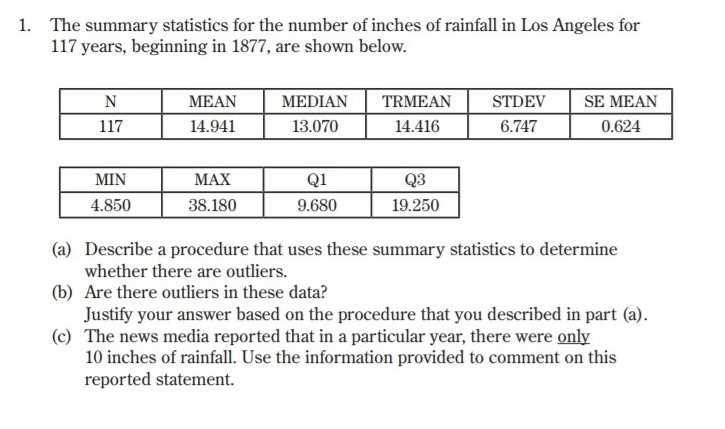
The structure of this academic evaluation is designed to challenge students’ comprehension and application of core concepts. It consists of multiple sections, each focusing on different areas of knowledge, and requires critical thinking as well as problem-solving skills. The format encourages a well-rounded approach, assessing both theoretical understanding and practical application of principles.

The first section typically includes a series of multiple-choice questions, where students must choose the correct response based on their ability to interpret data, analyze relationships, and identify patterns. These questions test speed and accuracy, making it crucial to understand the fundamental principles and their real-world applications.

The second part is often a set of free-response questions, which demand more detailed solutions and explanations. Here, students are required to work through problems step by step, demonstrating their knowledge in greater depth. This section evaluates not only correctness but also the ability to clearly communicate reasoning and justify answers.

Each section is timed, adding an element of time management that further tests students’ efficiency in applying learned skills under pressure. By understanding the overall structure and focus areas, students can better prepare for each type of question and improve their chances of success in the evaluation.

Key Concepts Covered in Test 4C

This section focuses on the essential ideas and principles that are evaluated during the exercise. The questions are designed to assess your understanding and ability to apply various mathematical techniques to solve problems effectively. Key areas include data analysis, probability models, and drawing conclusions from sets of information.

Core Areas of Focus

Probability Theory: Understanding different probability distributions, calculating probabilities, and working with conditional probabilities.
Data Interpretation: Analyzing and interpreting numerical data through graphical representations and identifying patterns.
Inference Techniques: Drawing conclusions based on sample data and applying concepts such as confidence intervals and hypothesis testing.

Important Techniques and Methods

Sampling Methods: Understanding random sampling, stratified sampling, and other techniques to ensure unbiased results.
Linear Regression: Analyzing the relationship between variables through regression analysis and making predictions.
Chi-Square Tests: Using chi-square tests for independence and goodness-of-fit tests to assess relationships between categorical variables.

Familiarity with these core concepts will help you navigate the different sections and perform well in solving related problems during the assessment.

Effective Strategies for Solving Statistics Problems

Approaching complex mathematical problems requires a structured strategy to ensure that each step is clear and methodical. Developing a strong problem-solving process not only helps in reaching the correct solution but also minimizes errors and improves efficiency under time constraints.

Organize Your Approach

Read Carefully: Begin by reading the question thoroughly, identifying key data and what is being asked. This step ensures that you don’t miss important details.
Break Down the Problem: Divide the problem into smaller, manageable parts. Solving each part sequentially makes the overall task less overwhelming.
Draw Visuals: Whenever possible, create charts, graphs, or diagrams to visualize the data. This helps in better understanding and interpreting the information.

Apply Problem-Solving Techniques

Use Formulas Wisely: Familiarize yourself with relevant formulas and when to apply them. Ensure that you understand the underlying concepts behind each formula.
Check Units: Always keep track of the units of measurement. Converting units correctly is crucial in solving problems involving real-world data.
Estimate Before Solving: Make rough estimates before performing detailed calculations. This step can help you avoid making large mistakes and ensures that your final answer is reasonable.

By employing these strategies, you can improve both your accuracy and speed in solving challenging problems, building confidence as you progress through each question.

Common Challenges Faced in AP Exams

Students often encounter various obstacles during academic evaluations that test their understanding of complex concepts. These challenges may stem from the difficulty of the material, the time constraints, or the pressure to perform. Recognizing and addressing these issues can greatly enhance performance and reduce anxiety on exam day.

Time Management and Efficiency

One of the most frequent challenges is managing the limited time allocated for each section. Many students struggle to complete all questions, especially in sections that require detailed calculations or lengthy explanations. Prioritizing tasks and focusing on the more straightforward problems first can help alleviate this pressure.

Understanding Complex Problem Types

Another common issue is the difficulty in interpreting complex problems, particularly when they involve multiple concepts or require multi-step reasoning. It is essential to carefully read the instructions, break the problem into smaller steps, and focus on understanding the core concepts before attempting a solution.

Challenge	Solution
Time Constraints	Practice under timed conditions to improve speed and accuracy.
Difficulty with Word Problems	Identify key information, create visual aids, and break down the steps.
Confusion with Complex Formulas	Review and memorize essential formulas; practice their application.

By preparing for these challenges in advance, students can approach their exams with confidence, ensuring that they are better equipped to handle the more difficult tasks that may arise.

Detailed Solutions for Probability Questions

Probability questions often require a clear understanding of mathematical principles and the ability to apply them to solve real-world problems. These types of problems can vary in complexity, but with the right approach, each one can be broken down into manageable steps. The key to solving probability problems is to understand the fundamental concepts and apply them systematically.

When tackling probability problems, it is essential to start by identifying the type of scenario presented. For example, whether it’s a simple event, compound event, or conditional probability, recognizing the situation will guide you in choosing the correct method for solving the problem. Once the problem is understood, it’s important to outline all possible outcomes, assign probabilities where applicable, and calculate based on the specific rules that govern the situation.

Following a structured approach helps ensure that no step is missed. For instance, with simple probability, we use the ratio of favorable outcomes to total outcomes. For more complex situations, such as conditional probability, the formula P(A|B) = P(A ∩ B) / P(B) can be applied, considering the relationship between events A and B. By breaking down each problem into smaller tasks, it becomes easier to identify errors and avoid confusion.

Through consistent practice and mastering these techniques, students can build the confidence to approach and solve any probability question effectively, ensuring a thorough understanding of the concepts involved.

Analyzing Data Interpretation Problems

Data interpretation problems require careful examination of given information, often presented in the form of tables, charts, or graphs. The ability to extract meaningful insights from these visuals is critical for solving related questions. These tasks test how well you can analyze raw data, identify trends, and draw conclusions based on the presented figures.

Steps to Approach Data Interpretation

Examine the Visuals: Start by carefully reviewing the graph or table. Pay attention to the axes, labels, and units of measurement to understand the data’s context.
Identify Patterns: Look for trends or relationships within the data, such as increases, decreases, or any correlations between variables.
Analyze Specific Data Points: Focus on key data points or changes, and make sure you understand their significance within the broader context of the problem.

Common Mistakes to Avoid

Ignoring Units: Always check the units of measurement. Misinterpreting units can lead to incorrect conclusions.
Overlooking Important Information: Often, key data points are hidden in larger datasets. Carefully read every part of the visual to avoid missing crucial details.
Rushing to Conclusions: Take your time to analyze the data fully before drawing conclusions. Premature assumptions can lead to errors.

Problem Type	Key Approach
Bar Graphs	Compare the heights of bars and identify trends or differences in categories.
Pie Charts	Examine the proportions of different sections to assess relative sizes or changes over time.
Tables	Look for patterns in rows and columns; pay attention to totals and averages.

By following these strategies and avoiding common pitfalls, you can improve your ability to interpret data accurately and answer questions related to it with confidence.

Tips for Tackling Complex Calculations

When faced with intricate mathematical calculations, it’s essential to approach each problem methodically. Breaking down complex steps into manageable parts and applying the right techniques can prevent confusion and lead to more accurate results. This section highlights useful strategies to improve your efficiency and precision when solving detailed mathematical problems.

Approach to Complex Problems

Understand the Problem: Begin by carefully reading the question and identifying what is being asked. Highlight key values and relationships in the problem.
Break It Down: Divide the problem into smaller, simpler components. Solve each part step-by-step, ensuring you are not overwhelmed by the complexity.
Organize Your Work: Write down intermediate steps to avoid skipping any crucial calculation. This also makes it easier to spot any mistakes.

Useful Techniques for Efficiency

Use Approximation: When dealing with large numbers or decimals, consider approximating values to simplify calculations, especially in multi-step problems.
Double-Check Units: Ensure that all units are consistent throughout the calculations. This avoids mistakes, especially in problems involving rates or conversions.
Review Formulae: Be sure you are applying the correct formula for each situation. Understanding the logic behind the formula is crucial for correct usage.

By following these tips, you can approach complex mathematical challenges with more confidence, improving both accuracy and speed in your calculations.

Insights into Statistical Hypothesis Testing

Hypothesis testing is a fundamental concept that helps determine the validity of assumptions or claims based on data. It provides a structured method for assessing whether the observed evidence supports a specific claim or if the results are simply due to chance. Understanding the process and the logic behind hypothesis testing is crucial for interpreting results and making informed decisions.

The Hypothesis Testing Process

Formulating Hypotheses: Start by defining two competing hypotheses: the null hypothesis (typically stating no effect or no difference) and the alternative hypothesis (suggesting the presence of an effect or difference).
Choosing the Significance Level: The significance level (often denoted as α) is the threshold for determining whether the results are statistically significant. Common choices are 0.05 or 0.01.
Calculating the Test Statistic: Depending on the type of data, calculate the appropriate test statistic (e.g., z-score, t-value) using the sample data.
Making a Decision: Compare the test statistic to critical values, and determine whether to reject or fail to reject the null hypothesis based on the significance level.

Common Pitfalls in Hypothesis Testing

Misinterpreting p-values: A p-value indicates the probability of observing data as extreme as the sample data, given that the null hypothesis is true. It does not directly measure the strength of the hypothesis itself.
Ignoring Assumptions: Each test has underlying assumptions, such as normality or independence of observations. Violating these assumptions can lead to incorrect conclusions.
Overlooking Effect Size: Statistical significance does not necessarily imply practical significance. It’s essential to consider the effect size to understand the real-world relevance of the findings.

Mastering the principles of hypothesis testing allows for more informed decision-making, providing a solid foundation for analyzing data and drawing conclusions in a variety of fields.

How to Approach Graph-Based Questions

Graph-based questions require careful analysis of visual representations of data. Whether it’s a bar chart, line graph, or scatter plot, these questions test your ability to interpret trends, relationships, and key insights from graphical data. The goal is to extract meaningful information and apply it to answer specific questions accurately.

When faced with graph-based problems, start by thoroughly reviewing the graph and understanding the context. Pay attention to the labels, scales, and units on both axes. These elements are crucial for accurately interpreting the data. Next, look for key features such as peaks, troughs, or any notable patterns that could be central to answering the question.

It’s also important to consider the type of graph being presented. Different graph types are used to highlight specific relationships in the data, and each one requires a slightly different approach. For example, line graphs are often used to show trends over time, while bar charts compare different categories. Understanding the purpose of the graph will guide your analysis and help you focus on the most relevant details.

Using Formulas Efficiently in Statistics

Formulas play a crucial role in solving problems that involve quantitative analysis. Understanding how to apply them correctly and efficiently can save time and ensure accurate results. This section will provide guidance on how to use mathematical formulas effectively to simplify complex calculations and improve problem-solving accuracy.

Key Tips for Applying Formulas

Understand the Concept: Before applying a formula, make sure you fully understand the underlying concept it represents. This will help you know when and why to use it appropriately.
Break Down the Formula: If the formula involves multiple steps, break it down into smaller parts. Solve each part step by step to avoid mistakes.
Organize Information: Before applying any formula, organize all the given values and variables clearly. Having a well-organized setup will help you avoid missing crucial details.

Common Formulas and Their Applications

Mean: Used to calculate the average of a dataset. This formula involves summing all values and dividing by the total number of values.
Variance and Standard Deviation: Essential for understanding the spread or dispersion of a dataset. These formulas help you quantify how much the values deviate from the mean.
Probability Formulas: Used to calculate the likelihood of events. Understanding conditional probability and the use of combinations or permutations can be valuable for solving related problems.

By mastering these formulas and knowing when to apply them, you can streamline your approach to quantitative problems and enhance the accuracy of your results.

Breakdown of Key Mathematical Techniques

Mathematical techniques are essential for solving a wide range of problems in quantitative analysis. These methods help transform complex situations into manageable steps, allowing for more precise and efficient solutions. By understanding and mastering these techniques, you can approach various problems with confidence and clarity.

Core Techniques and Their Applications

Algebraic Manipulation: The ability to simplify expressions, solve equations, and manipulate formulas is fundamental. This skill is used in a variety of problems to isolate variables and solve for unknowns.
Linear Relationships: Identifying and working with linear relationships is crucial in many applications. Techniques like solving linear equations, finding slopes, and interpreting intercepts help in analyzing data that follows a straight-line pattern.
Summation and Averages: Calculating sums, means, and averages is often the first step in analyzing data. Techniques like summation notation help simplify the process of working with large datasets.

Advanced Techniques for Complex Problems

Probability Theory: Understanding the fundamentals of probability allows you to assess the likelihood of different outcomes. Techniques like conditional probability and Bayes’ theorem are used to model uncertain events and predict outcomes more accurately.
Regression Analysis: Regression methods are used to understand relationships between variables. Linear regression, in particular, is a powerful technique for predicting values based on historical data.
Optimization Methods: Techniques like differentiation or linear programming are used to find the optimal solution to problems, such as minimizing costs or maximizing efficiency.

By mastering these mathematical techniques, you gain a toolkit to break down complex problems, apply logical reasoning, and reach accurate solutions. With practice, these methods become invaluable tools in both academic and real-world contexts.

Understanding Real-World Application Problems

Real-world application problems bridge the gap between theoretical knowledge and practical usage. These problems require not only a deep understanding of core concepts but also the ability to apply them to solve everyday challenges. Whether it’s predicting trends, analyzing behavior, or optimizing processes, the ability to approach real-world problems with a structured methodology is crucial for effective problem solving.

Breaking Down Real-World Scenarios

When faced with an application problem, the first step is to identify the key components of the situation. Often, these problems are presented in a contextual manner, such as analyzing sales data, predicting customer behavior, or assessing risk in financial markets. By translating these scenarios into mathematical models or systems, it becomes easier to apply the right techniques for finding solutions.

Key Elements to Focus On

Element	Explanation
Data Identification	Determine what information is given and what needs to be derived from the data. Ensure all variables and units are clearly understood.
Problem Context	Understand the broader situation surrounding the problem, such as the industry, timeframe, or specific goals being targeted.
Method Selection	Choose the appropriate mathematical techniques based on the nature of the problem–whether it’s a probability model, regression, or optimization method.
Interpretation of Results	Once a solution is derived, it’s important to interpret the results in a meaningful way that aligns with the problem’s context and objectives.

By following a logical process and ensuring that all variables are accounted for, you can successfully tackle real-world application problems. Whether the focus is on business, economics, or social sciences, the ability to break down complex situations into solvable components is essential for reaching effective conclusions.

Time Management Tips for AP Statistics

Effective time management is crucial for mastering complex topics and performing well on exams. By allocating time wisely and approaching each section strategically, students can maximize their understanding and minimize stress. Whether you are reviewing material or tackling practice questions, managing your time efficiently allows you to cover all essential concepts without feeling overwhelmed.

Prioritize Key Concepts

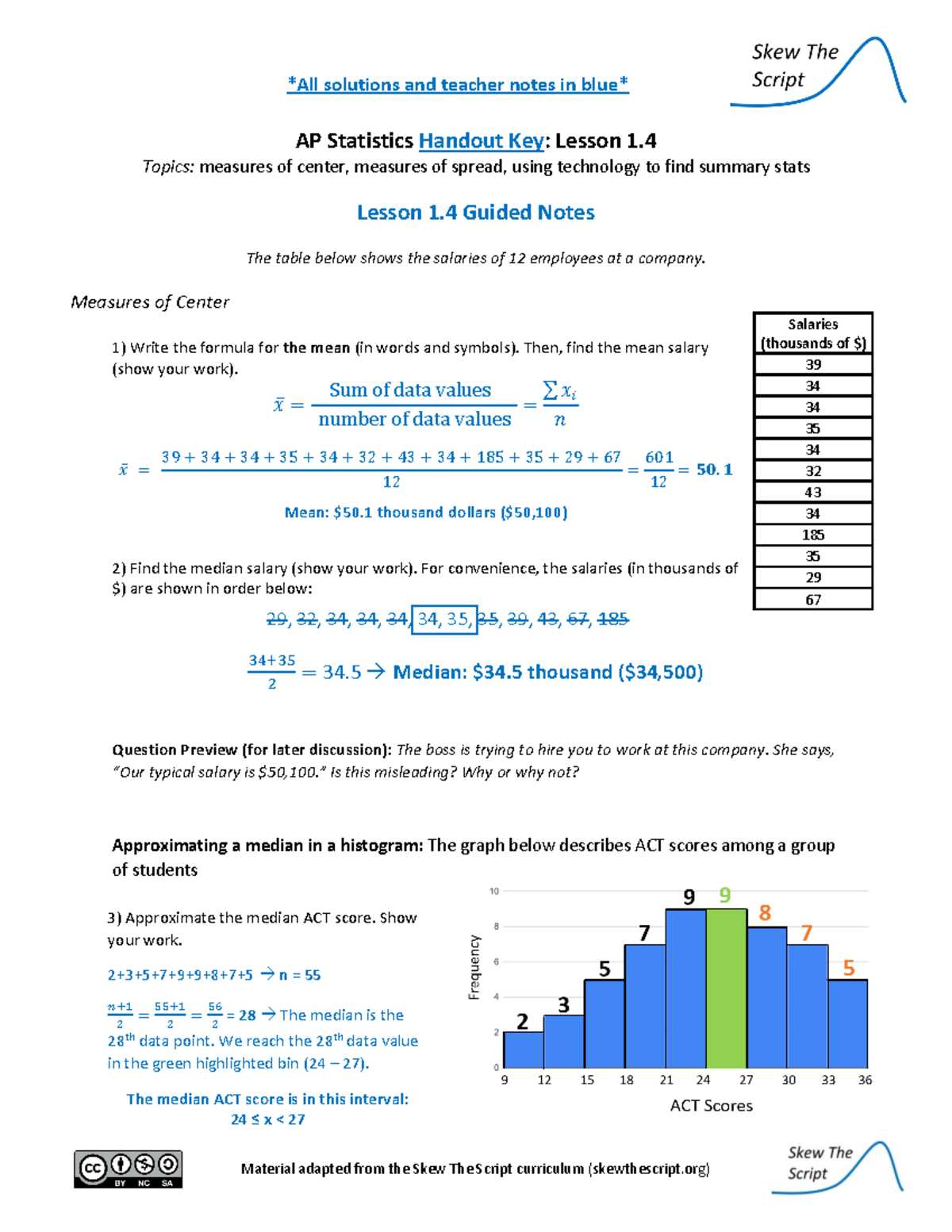
Start by identifying the most important topics that require attention. Some concepts may appear more frequently on exams, while others could be more challenging to grasp. Focus on mastering these areas early in your study plan, leaving time for review and practice closer to the exam date.

Use a study calendar: Break down your study schedule into manageable chunks and dedicate specific days to different topics.
Review past exams: Analyzing past questions will give you insight into which areas are commonly tested, helping you prioritize your efforts.
Track your progress: Regularly assess your understanding to ensure that you are staying on track with your study goals.

Practice Under Timed Conditions

To build speed and accuracy, it’s important to simulate real exam conditions. Set time limits for practice problems and complete them in a focused, uninterrupted environment. This not only helps you become accustomed to the time constraints but also enables you to identify areas where you may need further improvement.

Timed practice sessions: Allocate specific time slots for practice, aiming to complete each section within the given time limits.
Evaluate your pacing: Assess whether you are spending too much time on any particular question or section and adjust your strategy accordingly.

By following these time management strategies, you can effectively balance studying, practicing, and reviewing while ensuring that you are prepared and confident come exam day.

Importance of Reviewing Test Solutions

Reviewing the solutions to practice problems or past exams plays a critical role in reinforcing learning and improving performance. By carefully analyzing the steps taken to arrive at the correct answers, students can gain deeper insights into the reasoning behind each problem. This process helps to identify areas of weakness and enhances overall understanding.

Identifying Mistakes and Gaps in Knowledge

One of the main benefits of reviewing solutions is the opportunity to spot mistakes and gaps in knowledge. Even after completing a problem, it’s easy to overlook small errors or misunderstandings. By reviewing the solutions, you can pinpoint these issues and take steps to address them.

Understand where you went wrong: If you made an error, trace it back to see where your reasoning diverged from the correct path.
Identify knowledge gaps: Some mistakes may reveal gaps in your understanding that need to be filled before the exam.
Improve accuracy: Recognizing common errors helps you avoid repeating them in future practice or during the actual exam.

Building Problem-Solving Strategies

Reviewing the solutions also helps to build effective problem-solving strategies. By studying the correct approach, you can learn how to organize your thoughts, manage time more efficiently, and use the most appropriate methods for different types of questions.

Learn efficient techniques: Seeing multiple ways to solve a problem allows you to choose the most efficient technique in future situations.
Develop a consistent approach: Regularly reviewing solutions helps to build a structured approach to tackling complex problems.
Strengthen conceptual understanding: Understanding why certain steps are taken in a solution ensures that you retain important concepts for the long term.

Incorporating solution reviews into your study routine not only solidifies your knowledge but also prepares you for a wide range of challenges, improving your confidence and performance on exam day.