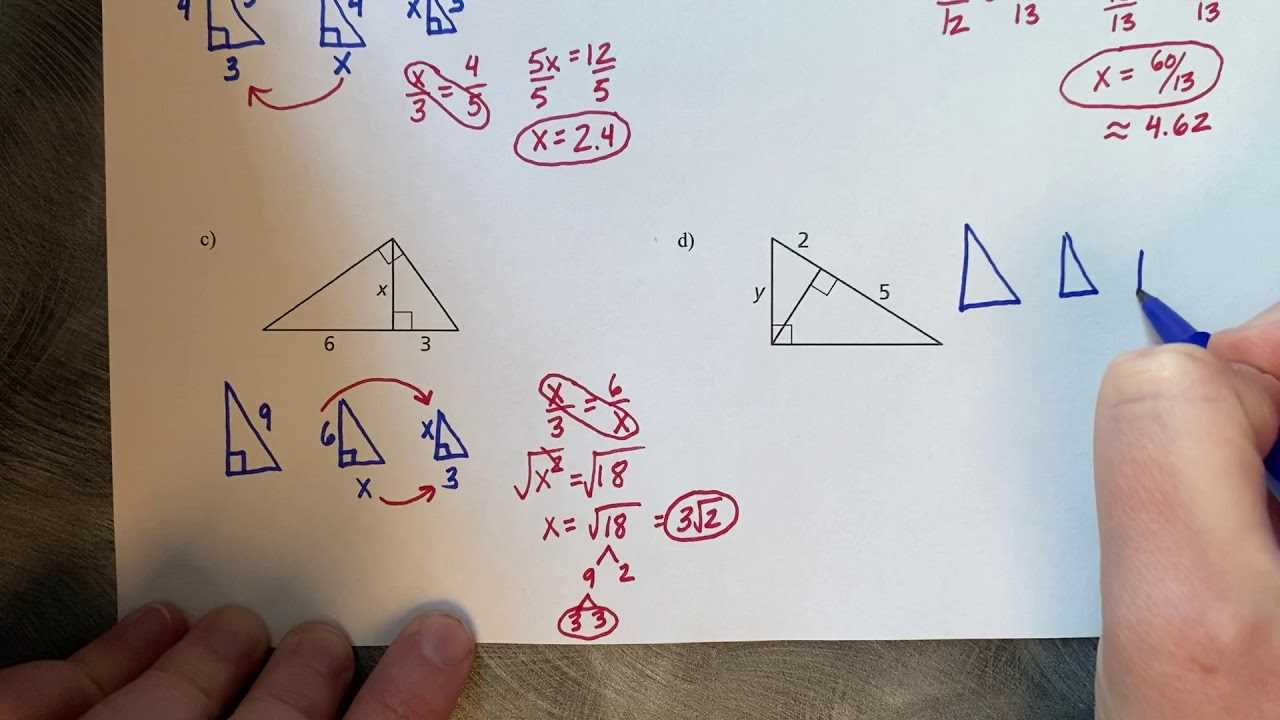
Understanding the core principles of shapes, angles, and spatial relationships is essential for mastering mathematical challenges. This section provides structured solutions to common problems, helping learners gain clarity and confidence in their studies. Whether you’re struggling with complex figures or looking for a clearer understanding of basic concepts, this guide offers detailed explanations and helpful strategies.
Detailed steps and logical methods are broken down to make tackling geometric problems more approachable. With these resources, you’ll be able to strengthen your skills and apply them effectively across various exercises. Each solution is designed to enhance your understanding and provide practical tools for future tasks.
By examining each example closely, students can familiarize themselves with the processes involved and avoid common errors. With focused practice, these techniques will become second nature, allowing learners to approach even the most challenging problems with ease.
Comprehensive Solutions for Geometric Challenges
Mastering spatial reasoning and shapes is a crucial part of building a strong foundation in advanced problem-solving. By exploring various resources designed to provide clear solutions, students can improve their understanding of geometric concepts and apply them confidently in both academic and real-world contexts.
Why This Resource is Valuable
This guide is tailored to support learners by offering structured, step-by-step solutions to the most common types of geometric problems. With a focus on clarity and accuracy, students can break down complex problems into manageable steps, making the learning process smoother and more intuitive.
How to Use These Solutions Effectively
- Start by reviewing the examples thoroughly to understand the reasoning behind each step.
- Focus on the underlying principles and formulas used in the solution process.
- Practice solving similar problems to reinforce your knowledge and improve your skills.
- Use the solutions as a guide for tackling more challenging exercises.
Incorporating these strategies into your study routine can help build problem-solving confidence and deepen your understanding of geometric principles. By following the provided examples and practicing regularly, you’ll be prepared to tackle a wide variety of geometric tasks with ease.
Understanding Geometry with Big Ideas
Grasping the fundamental concepts of shapes, their properties, and the relationships between them is essential for building a strong mathematical foundation. This section explores how mastering these core concepts can unlock the ability to solve more complex problems with ease. By focusing on key principles, students can gain the tools necessary to approach challenges with confidence and clarity.
Core Principles to Focus On

To truly understand the subject, it’s important to focus on the essential elements such as angles, lines, and measurements. Once these basic principles are well-understood, more advanced topics like area, volume, and the relationships between different figures become much easier to comprehend. The goal is to build a strong understanding of these concepts before moving on to more intricate problems.
Building Confidence Through Practice
One of the most effective ways to solidify your understanding is through regular practice. By applying the core concepts to a variety of exercises, students can develop a deeper understanding and improve their problem-solving skills. The more problems are solved, the more intuitive these principles will become, allowing learners to tackle new challenges with increased confidence.
Key Concepts in Geometry Explained
Understanding the fundamental elements that define shapes and their properties is crucial for solving geometric problems. These basic principles serve as the foundation for more advanced concepts, making it essential to grasp them thoroughly. By breaking down these core ideas, learners can navigate through complex tasks with greater ease and precision.
Essential Principles to Master
- Points, Lines, and Angles: These are the building blocks of all geometric figures. Understanding their relationships is key to mastering the subject.
- Shapes and Figures: Familiarity with common shapes such as triangles, squares, and circles is essential for solving problems related to area, perimeter, and volume.
- Symmetry and Transformations: Recognizing how shapes can be reflected, rotated, or translated is an important skill in both theoretical and applied geometry.
- Proportions and Ratios: The relationships between various parts of a figure, especially in similar shapes, are fundamental for solving problems involving scaling and measurements.
Why These Concepts Matter
Mastering these core principles allows for a deeper understanding of more complex topics. Whether dealing with angles in polygons or calculating the area of irregular shapes, a solid grasp of the basics ensures that learners can approach new challenges confidently and accurately.
How to Use the Answer Key
Utilizing a solution guide effectively can significantly improve your understanding and problem-solving skills. Rather than simply copying solutions, it’s important to focus on the process and logic behind each step. By analyzing how each problem is solved, you can learn valuable techniques that will help you solve similar problems independently in the future.
Start by attempting to solve the problem on your own. Once you have made an effort, refer to the provided solutions to check your work. Compare your method to the one in the guide and identify any differences. Understanding why the steps in the solution are taken will deepen your comprehension of the material.
Don’t just rely on the answers for confirmation. Take the time to work through each step in the solution, reflecting on how each one contributes to the final result. This approach will enhance your skills and build a stronger foundation for future problems.
Common Geometry Problems Solved
There are several common challenges that students face when studying shapes, measurements, and spatial relationships. Addressing these typical issues can help build a strong foundation and improve problem-solving skills. By breaking down these problems into manageable steps, it becomes easier to understand and apply the necessary techniques.
Area and Perimeter of Simple Shapes: One of the most frequent tasks involves calculating the area and perimeter of basic figures like squares, rectangles, and circles. These calculations rely on fundamental formulas that can be easily applied once the correct dimensions are identified.
Example: To calculate the area of a rectangle, multiply its length by its width. For a circle, use the formula πr², where r is the radius.
Solving for Angles: Another common issue is finding unknown angles in various polygons. Whether working with triangles, quadrilaterals, or other multi-sided shapes, the ability to apply angle sum rules is essential.
Example: In a triangle, the sum of all angles equals 180°. Knowing this rule helps in finding missing angles when two are provided.
By practicing these types of problems and reviewing step-by-step solutions, students can gain confidence and tackle even more complex challenges in the future.
Step-by-Step Solutions for Students

Breaking down complex problems into smaller, manageable steps is essential for mastering any subject. This approach not only helps students understand the process but also builds confidence in their ability to solve challenging tasks independently. By following a clear sequence of actions, learners can tackle problems systematically and efficiently.
How to Approach Each Problem
Start by carefully reading the problem and identifying what is being asked. Highlight the key information and relevant details, such as given measurements or known formulas. Once the essentials are clear, determine which mathematical principles or strategies apply to the situation. Then, proceed step by step, checking each part of the solution before moving forward.
Benefits of the Step-by-Step Method
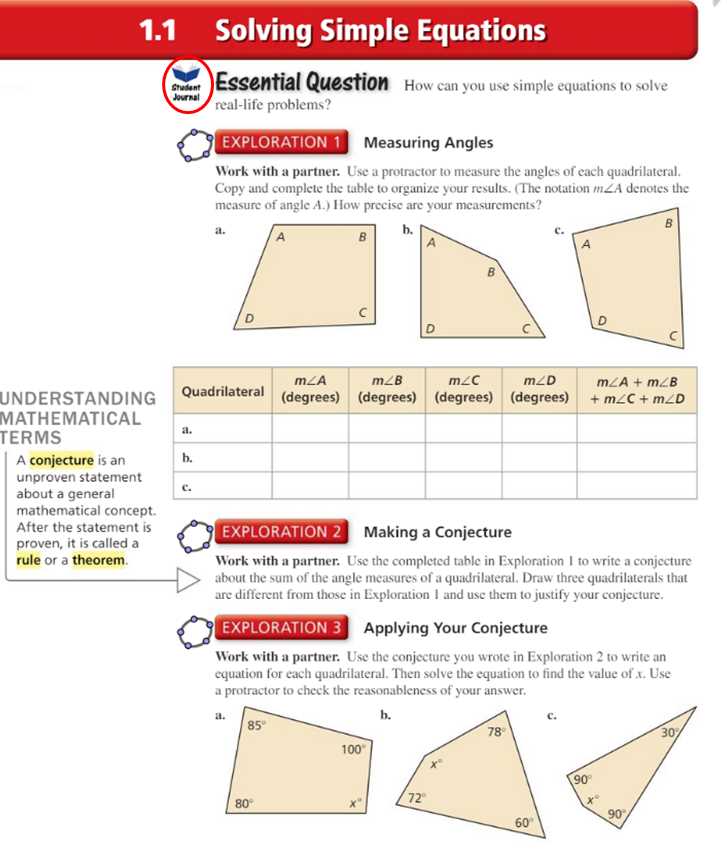
- Helps break down complex problems into simpler, more understandable tasks.
- Ensures that all necessary steps are followed for an accurate solution.
- Promotes logical thinking and problem-solving skills, which are valuable beyond just solving mathematical exercises.
By adopting this structured method, students can approach even the most difficult tasks with greater clarity and confidence, ensuring a deeper understanding of the concepts involved.
Mastering Geometric Formulas
Having a strong command of the fundamental formulas used to calculate areas, volumes, and other properties of shapes is essential for solving a wide range of problems. Mastery of these formulas allows students to quickly identify the right approach and efficiently apply them in various scenarios. A deep understanding of when and how to use these formulas is key to building problem-solving confidence and accuracy.
Essential Formulas to Know
- Area of a Rectangle: Length × Width
- Area of a Triangle: 1/2 × Base × Height
- Perimeter of a Rectangle: 2 × (Length + Width)
- Circumference of a Circle: 2 × π × Radius
- Volume of a Rectangular Prism: Length × Width × Height
- Surface Area of a Sphere: 4 × π × Radius²
How to Apply Formulas Effectively
- Identify the shape or figure involved and gather all necessary measurements.
- Determine which formula corresponds to the shape or problem type.
- Carefully substitute the known values into the formula.
- Double-check your calculations to ensure accuracy and avoid errors.
By practicing regularly with these formulas, students can develop a quick and intuitive understanding of how to apply them in various contexts, making complex problems much more manageable.
Improving Geometry Skills Through Practice
Enhancing your understanding of spatial relationships and properties requires consistent practice. By regularly working through a variety of problems, you can reinforce key concepts, sharpen your problem-solving abilities, and become more confident in your skills. Repetition not only helps solidify knowledge but also prepares you for more complex challenges by building a strong foundation of core principles.
Effective Practice Strategies
- Start with Simple Problems: Begin by solving basic problems to ensure a solid grasp of fundamental concepts before moving on to more complex tasks.
- Work on a Variety of Problem Types: Tackle different types of problems–such as area, volume, and angle calculations–to broaden your understanding of the subject.
- Track Your Mistakes: When errors occur, take time to review and understand them. This helps in identifying areas that need improvement.
- Set Time Limits: Practice solving problems within a set timeframe to improve both accuracy and speed under pressure.
Why Consistency Matters
- Regular practice leads to familiarity with concepts, reducing anxiety during exams or real-life applications.
- It improves your ability to recognize patterns and apply learned strategies to new situations.
- Through consistent effort, you can gradually master even the most challenging concepts, ultimately increasing your overall proficiency.
By adopting these strategies and committing to frequent practice, you’ll be well on your way to mastering spatial reasoning and enhancing your problem-solving capabilities.
Tips for Tackling Difficult Geometry Questions
When faced with challenging problems involving shapes and spatial relationships, it can be easy to feel overwhelmed. However, with the right approach and mindset, you can effectively break down complex questions into manageable steps. The key is to remain calm, carefully analyze the problem, and apply a systematic strategy to find a solution.
Step-by-Step Approach
- Understand the Problem: Carefully read the problem and identify all given information. Highlight key measurements, shapes, or any specific instructions provided in the question.
- Draw a Diagram: If not provided, sketching a diagram can help visualize the situation and make it easier to see relationships between elements.
- Identify Relevant Formulas: Think about which principles or formulas apply to the specific problem. Review your notes or reference materials to find the right ones.
- Work Through the Problem Step-by-Step: Break the problem into smaller, logical steps. Avoid skipping any part of the process, and check your work as you go.
Additional Strategies
- Look for Symmetry: Many problems involve symmetrical shapes, which can simplify calculations and make it easier to identify missing information.
- Use Logical Reasoning: If the problem feels too complex, think through each step carefully. Often, logical reasoning can help eliminate unnecessary steps and lead you to the solution faster.
- Don’t Rush: Take your time. Sometimes, slowing down and reevaluating the problem can reveal important details that you may have initially overlooked.
By following these strategies, you can develop a methodical approach to even the toughest questions and build your confidence in solving complex problems.
Benefits of Using an Answer Key
Having access to a solution guide can be an invaluable resource for learners looking to check their work, understand problem-solving techniques, and reinforce their knowledge. By comparing their solutions to the provided solutions, students can identify errors, understand the correct process, and gain insight into more efficient ways of approaching tasks. This tool serves as both a guide and a learning aid, promoting a deeper understanding of the concepts involved.
| Benefit | Description |
|---|---|
| Correctness Verification | Quickly confirms whether solutions are correct, saving time in identifying mistakes and boosting confidence. |
| Learning Efficient Strategies | Helps identify the most effective methods for solving problems, which can be applied to future tasks. |
| Building Understanding | Clarifies the reasoning behind specific steps, allowing for a deeper grasp of the material and concepts. |
| Identifying Mistakes | Helps pinpoint errors in reasoning or calculation, providing an opportunity to correct and learn from them. |
| Improved Problem-Solving Skills | By regularly reviewing solutions, learners can develop better strategies and approaches to difficult problems. |
By using this valuable tool as part of your study routine, you can enhance both your confidence and your ability to solve complex problems effectively and accurately.
Common Mistakes and How to Avoid Them
While working through problems involving spatial reasoning and shapes, it’s easy to make certain errors that can lead to incorrect conclusions. These mistakes often stem from misunderstandings of key concepts, rushing through steps, or overlooking important details. By recognizing these common pitfalls, students can take proactive steps to avoid them, ensuring a more accurate and efficient approach to solving problems.
| Mistake | How to Avoid It |
|---|---|
| Misinterpreting the Question | Read the problem carefully and underline key information. Double-check that you understand what is being asked before proceeding. |
| Skipping Steps in the Solution | Work through each step methodically, even if it seems repetitive. Skipping intermediate steps can result in miscalculations and confusion. |
| Forgetting Units of Measurement | Always include units when solving problems, and make sure they match across the problem. Convert units as needed to ensure consistency. |
| Using Incorrect Formulas | Familiarize yourself with the correct formulas and their applications. Double-check that you’re using the appropriate one for each situation. |
| Rushing Through Calculations | Take your time to carefully perform each calculation. If necessary, verify your results before moving on to the next step. |
By staying mindful of these common mistakes and following best practices, you can improve both the accuracy and efficiency of your problem-solving process, leading to better results overall.
How to Approach Word Problems in Geometry
Word problems in the realm of shapes and spatial reasoning can seem intimidating at first glance, but with the right approach, they become more manageable. The key is to break the problem down into smaller, more digestible parts and to identify the important details. By focusing on the given information and translating it into a clear visual representation, you can determine the best method for solving the problem step by step.
1. Read the Problem Carefully
The first step in tackling a word problem is to read it thoroughly. Pay attention to the specific details provided, such as measurements, relationships between different shapes, or any conditions given in the question. It’s crucial to understand the context and to make note of any important information.
2. Identify the Key Variables
Once you have a clear understanding of the problem, identify the variables involved. These could include lengths, areas, angles, or other measurable elements. Writing down what each variable represents can help you stay organized and avoid confusion later on.
3. Draw a Diagram
If the problem involves complex shapes or configurations, drawing a diagram can make the problem much easier to understand. Label all known values on the diagram to help visualize the situation and establish relationships between the different elements.
4. Choose the Right Formula
Depending on the nature of the problem, certain formulas or principles may apply. Review the available formulas and select the one that fits the situation. Make sure to check that you have the correct formula before proceeding with any calculations.
5. Solve Step by Step
Work through the problem step by step. Take your time to avoid rushing through calculations. If you’re stuck, revisit your diagram or reconsider the relationships between the variables. Often, word problems are solved more easily when broken down into smaller, logical steps.
6. Double-Check Your Work
After reaching a solution, always review your work. Check your calculations, re-evaluate your diagram, and ensure that your answer makes sense within the context of the problem. This final step can help catch any mistakes before submitting your answer.
By following this structured approach, you’ll be better equipped to handle word problems and can solve even the most complex questions with greater confidence and accuracy.
Understanding Geometric Proofs and Theorems
In the study of spatial figures, understanding how to logically prove statements and apply established principles is essential. A proof is a structured argument that demonstrates the truth of a specific statement based on a series of logical steps and previously established facts. Theorems, on the other hand, are statements that have been proven through such logical reasoning. Mastery of both is crucial for solving complex problems and for building a strong foundation in the subject.
The Role of Logical Reasoning in Proofs
A proof involves a step-by-step explanation that moves from known facts to the desired conclusion. This process relies heavily on logical reasoning, where each step must be justified with a reason. It’s important to start from the basics and build up, ensuring that every assumption is supported by evidence. Proofs can be classified into different types, such as direct proofs, indirect proofs, and proofs by contradiction, each with its own method of validating a statement.
Common Theorems and Their Applications
Theorems form the backbone of geometric reasoning. These statements are proven based on previous knowledge and are often used to prove new results. Some of the most well-known theorems include the Pythagorean Theorem, which relates the sides of a right triangle, and the Sum of Angles in a Triangle Theorem. These theorems are powerful tools for solving problems and proving further geometric relationships.
By thoroughly understanding proofs and theorems, students can approach more complex problems with confidence, knowing that they have a solid foundation to rely on when tackling new challenges.
What to Expect in Big Ideas Math
As you embark on this educational journey, you’ll encounter a structured approach that guides you through essential concepts in spatial reasoning and measurement. The content is carefully designed to progressively build your understanding, from foundational principles to more advanced theories. Throughout your studies, you’ll not only learn theoretical knowledge but also gain practical skills for solving complex challenges.
Key Learning Objectives

The course provides a clear roadmap for students, outlining specific goals and benchmarks that should be achieved at each stage of learning. Some of the key objectives include:
- Developing a solid grasp of spatial relationships and properties.
- Mastering fundamental techniques for measuring and analyzing different shapes.
- Building proficiency in solving problems using logical reasoning and established principles.
- Applying mathematical concepts to real-world scenarios and everyday problems.
What You’ll Encounter in Lessons
The lessons are thoughtfully structured to ensure that students remain engaged while learning. You can expect to encounter:
- Clear explanations: Each topic is broken down into manageable sections, making complex ideas accessible and easy to understand.
- Interactive activities: These activities help reinforce theoretical knowledge and encourage active participation in learning.
- Practice problems: Regular exercises allow you to apply what you’ve learned, ensuring that the concepts stick and become second nature.
- Real-world connections: Lessons are designed to demonstrate the relevance of the concepts in everyday life, helping you see how they are applied beyond the classroom.
By engaging with the material, practicing regularly, and applying the concepts in various contexts, you’ll gain the necessary skills to excel in the subject and tackle even the most challenging topics with confidence.
How Answer Keys Enhance Learning
Providing solutions to problems not only helps verify results but also plays a crucial role in deepening understanding. When students have access to solutions, they are able to compare their methods and outcomes, identifying areas where they may have made mistakes or missed critical steps. This reflective process allows for a better grasp of the material, helping learners refine their skills.
One of the primary benefits of using solution sets is the opportunity for self-assessment. Students can test their understanding independently, using the provided solutions to evaluate their approach. This encourages active learning, as it motivates learners to identify their errors and work through the correct methodology. With each correction, students reinforce their knowledge, fostering improved problem-solving abilities.
In addition, these resources promote autonomy. By providing a structured path to follow, students can develop confidence in their ability to tackle challenges without constant guidance. This independence encourages more consistent practice and supports a deeper, more lasting retention of key concepts. Ultimately, the use of solutions not only helps students correct their work but also enhances their overall comprehension and proficiency in the subject.
Geometry Practice for Better Performance
Consistent practice is essential for mastering any subject, and the same holds true for spatial reasoning and problem-solving. By engaging in regular exercises, students can sharpen their understanding of essential concepts and techniques. This repeated exposure helps to build familiarity and confidence, enabling learners to apply their knowledge with greater ease and accuracy.
Focused practice allows individuals to address areas where they may be struggling and to reinforce their strengths. It provides an opportunity to experiment with different approaches and strategies, leading to a more versatile skill set. Whether through solving problems, reviewing concepts, or seeking out additional exercises, deliberate practice is key to enhancing performance.
| Type of Practice | Benefits |
|---|---|
| Solving Problems | Improves problem-solving skills and reinforces concepts. |
| Reviewing Formulas | Strengthens memory retention and understanding of key principles. |
| Applying Concepts in New Situations | Enhances ability to transfer knowledge to different contexts. |
| Timed Practice | Improves speed and accuracy under pressure. |
By integrating these different forms of practice, students can ensure they are well-prepared and equipped to perform at their best. Consistent and varied practice not only helps solidify foundational knowledge but also encourages the development of advanced skills, allowing students to tackle more complex challenges with confidence.
Improving Your Geometry Problem-Solving
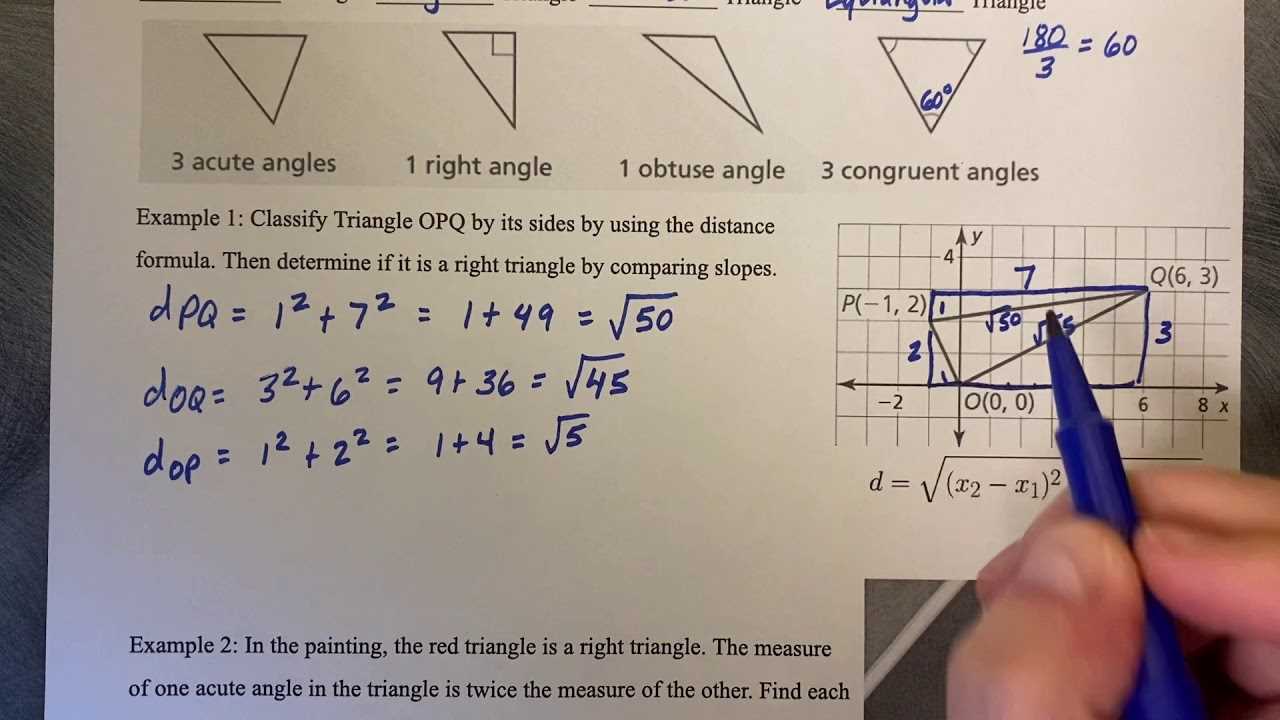
Enhancing problem-solving abilities requires a structured approach and consistent practice. Developing strong problem-solving skills allows you to tackle complex scenarios with greater ease, as it helps you identify patterns, apply appropriate methods, and reach solutions effectively. Whether you are working with shapes, angles, or calculations, there are key strategies that can improve your ability to solve problems in this area.
Key Strategies for Problem Solving

- Understand the Problem: Read the problem carefully and highlight the key information. Identifying what is asked and what is given can help clarify the approach.
- Draw Diagrams: Visual aids such as sketches or diagrams can simplify complex problems and help you see relationships between elements more clearly.
- Break It Down: Divide the problem into smaller, more manageable parts. Solving these smaller segments one at a time can make the overall problem seem less daunting.
- Use Logical Steps: Apply a logical sequence of steps to reach a solution. Being methodical ensures that no part of the problem is overlooked.
Common Mistakes to Avoid
- Rushing the Process: Moving too quickly can lead to careless mistakes. Take your time to analyze the problem thoroughly.
- Ignoring Units: Always pay attention to the units in the problem. Converting or mismatching units can result in incorrect solutions.
- Skipping the Check: After solving, double-check your work to ensure that the solution makes sense and satisfies all aspects of the problem.
By following these strategies and avoiding common pitfalls, you can significantly improve your ability to solve problems with precision and confidence. Regular practice, reflection, and learning from mistakes will further refine your skills and enable you to tackle more challenging problems successfully.
Key Resources for Geometry Success
Achieving success in spatial reasoning and shape-related problems requires a blend of effective tools, resources, and strategies. With the right materials, you can enhance your understanding, streamline your study process, and improve problem-solving techniques. Below are some vital resources that can aid in mastering this subject area.
Essential Study Materials
- Interactive Software: Programs and apps that simulate geometric concepts offer interactive learning experiences, making it easier to visualize and manipulate shapes and their properties.
- Textbooks and Practice Guides: Comprehensive textbooks provide theory, explanations, and example problems, while practice books offer targeted exercises to test your understanding.
- Online Tutorials: Websites and platforms with video tutorials allow learners to explore topics at their own pace, providing clear explanations and step-by-step solutions.
- Study Groups and Forums: Collaborating with peers or engaging in online communities can help you gain new perspectives, clarify doubts, and exchange useful tips.
Useful Tools for Problem Solving
| Tool | Purpose |
|---|---|
| Graphing Calculators | Assists in solving equations and visualizing graphs, helping to analyze complex problems. |
| Protractors and Rulers | Useful for measuring angles and distances when working with physical models or diagrams. |
| Online Geometry Solvers | Provides automated solutions and step-by-step guides for a variety of geometric problems. |
| Formula Sheets | Quick reference guides that summarize essential formulas, allowing for faster recall during problem solving. |
By utilizing these tools and resources, you can strengthen your understanding and enhance your performance in solving problems. Regular use of a variety of learning materials will help you tackle increasingly difficult topics with greater confidence and proficiency.