
In the realm of mathematics education, having clear and accessible explanations for each step of the problem-solving process is essential. Whether you’re tackling complex equations or refining your understanding of basic concepts, having organized support materials can greatly enhance your learning experience.
This section provides a thorough breakdown of the content, designed to guide you through each topic with precise, step-by-step instructions. These materials are tailored to help students strengthen their comprehension, providing clear solutions and valuable insights into solving challenging problems.
Mastering mathematical concepts becomes easier when every question is paired with a structured explanation. The following content will walk you through various stages of learning, ensuring you develop the skills needed to succeed and build confidence in solving problems independently.
By utilizing these resources, learners can improve their ability to tackle increasingly difficult tasks, with each explanation serving as a useful tool in mastering the subject matter effectively.
Comprehensive Guide to Problem Solutions
Effective learning in the field of mathematics requires access to well-organized support materials that clarify the reasoning behind each solution. By examining solutions in a structured manner, students can develop a deeper understanding of mathematical concepts, building confidence in their ability to approach problems on their own.
Step-by-Step Explanations for Each Topic
This section provides a detailed guide to solving mathematical problems, offering clear explanations for every stage of the process. Each section focuses on explaining the methods used to derive the correct solutions, ensuring that learners can follow along and grasp the concepts thoroughly.
Enhancing Problem-Solving Skills
Accessing well-structured solutions allows students to improve their problem-solving abilities. By working through each topic with these solutions, learners gain practical skills that enhance their overall understanding, helping them navigate complex tasks with ease and precision.
Overview of Mathematical Learning Support Tools
The materials provided in this section are designed to enhance students’ understanding of complex concepts. These tools are carefully organized to assist learners in grasping key ideas and mastering problem-solving techniques. Whether you’re reviewing fundamentals or diving into more advanced topics, these resources are aimed at providing clarity and structured guidance.
Key Features of the Learning Materials
Each resource offers distinct features that support effective learning:
- Clear explanations for each mathematical concept.
- Step-by-step breakdown of problem-solving methods.
- Practical examples for better understanding.
- Exercises to reinforce knowledge and skills.
How These Materials Enhance Learning
Utilizing these tools helps students approach problems with confidence and precision. The structure of the materials ensures that learners are guided through each task, gaining valuable insights as they progress. This systematic approach fosters a deeper comprehension of the subject matter, allowing students to improve their skills and apply them effectively.
How to Use the Answer Key Effectively
Utilizing the provided solutions guide can greatly enhance your understanding of complex topics. However, it’s essential to approach the material with a clear strategy to maximize its benefits. By following a few key practices, students can ensure they are not just finding the right answers, but also deepening their comprehension of the material.
Start by attempting each problem on your own before consulting the guide. This helps identify areas of confusion and encourages independent thinking. Once you review the solution, compare it with your own method to understand any differences. This approach not only helps in checking the correctness but also in refining your problem-solving skills.
In addition, use the explanations provided in the guide to understand the reasoning behind each step. If a particular method or concept is unclear, revisit the explanation and make sure you grasp the underlying principles before moving on. This ensures that you are truly learning and not just memorizing answers.
Lastly, integrate practice exercises into your study routine. Use the guide to verify your solutions, but always challenge yourself to complete problems without immediate reference. Over time, this will improve both your accuracy and confidence in solving similar problems on your own.
Chapter Breakdown for Mathematical Learning
Each section of the curriculum is carefully structured to introduce and build upon essential concepts. The material progresses from basic principles to more advanced topics, ensuring that students develop a solid foundation before tackling more complex problems. Understanding the progression of content is key to mastering the subject and retaining knowledge over time.
Each part of the guide focuses on a specific set of skills and ideas, offering a clear pathway for learners to follow. The topics are organized in a logical sequence, with each unit expanding on what was covered previously. This structured approach enables students to steadily improve their problem-solving abilities and gain a deeper understanding of the subject matter.
By reviewing the content in a step-by-step manner, learners can ensure that no crucial concept is overlooked. This breakdown also allows students to identify areas where they may need additional practice or clarification, helping them focus their efforts on specific problem areas.
Key Features of the Solution Guide
The solution guide is designed to provide clear and structured support for students as they work through problems. It offers detailed steps that help learners understand the reasoning behind each solution. By breaking down complex concepts into manageable parts, it ensures that students can follow the process and build their skills effectively.
Step-by-Step Explanations
Each problem is followed by a thorough explanation, highlighting the methods used to solve it. This allows learners to see not only the correct result but also the thought process behind each step. By following these instructions, students can reinforce their understanding of key techniques and apply them to future problems.
Practical Examples for Better Understanding
In addition to the solutions, the guide often includes relevant examples that provide additional context. These examples serve as a valuable resource for clarifying concepts and offering alternative methods of solving similar problems. Using these examples as a reference allows students to grasp various approaches and improve their problem-solving flexibility.
Understanding Chapter 1 Solutions
The first section of the curriculum sets the foundation for the entire course, introducing core concepts that are essential for progressing through more advanced topics. Grasping the solutions provided in this part is crucial for building a solid understanding of the subject. By breaking down each solution methodically, students can easily follow the logic and see how each concept applies to different problems.
As you work through the explanations, focus on understanding the reasoning behind each step rather than simply memorizing the answers. This approach will help you build a deeper understanding of the techniques used, enabling you to apply them confidently to a wide range of problems. The first set of solutions serves as a stepping stone, preparing you for more complex tasks as the course progresses.
Tips for Solving Math Problems
Approaching problems effectively requires more than just knowing the correct formulas. It’s about understanding the process, recognizing patterns, and developing strategies to tackle each challenge with confidence. By applying a few helpful tips, students can enhance their problem-solving abilities and improve their overall performance.
Start by carefully reading the problem and identifying key information. Break the problem down into smaller, more manageable parts, and tackle each step one at a time. Stay organized by writing down all necessary calculations and keeping track of your work, as this will help you avoid mistakes and stay focused. Additionally, always double-check your results by plugging them back into the original problem.
Practice is essential to mastering problem-solving. The more problems you solve, the better you’ll understand how to approach similar challenges in the future. Don’t hesitate to revisit earlier problems to reinforce your understanding and identify any areas that may require additional practice.
Using Resources for Extra Practice
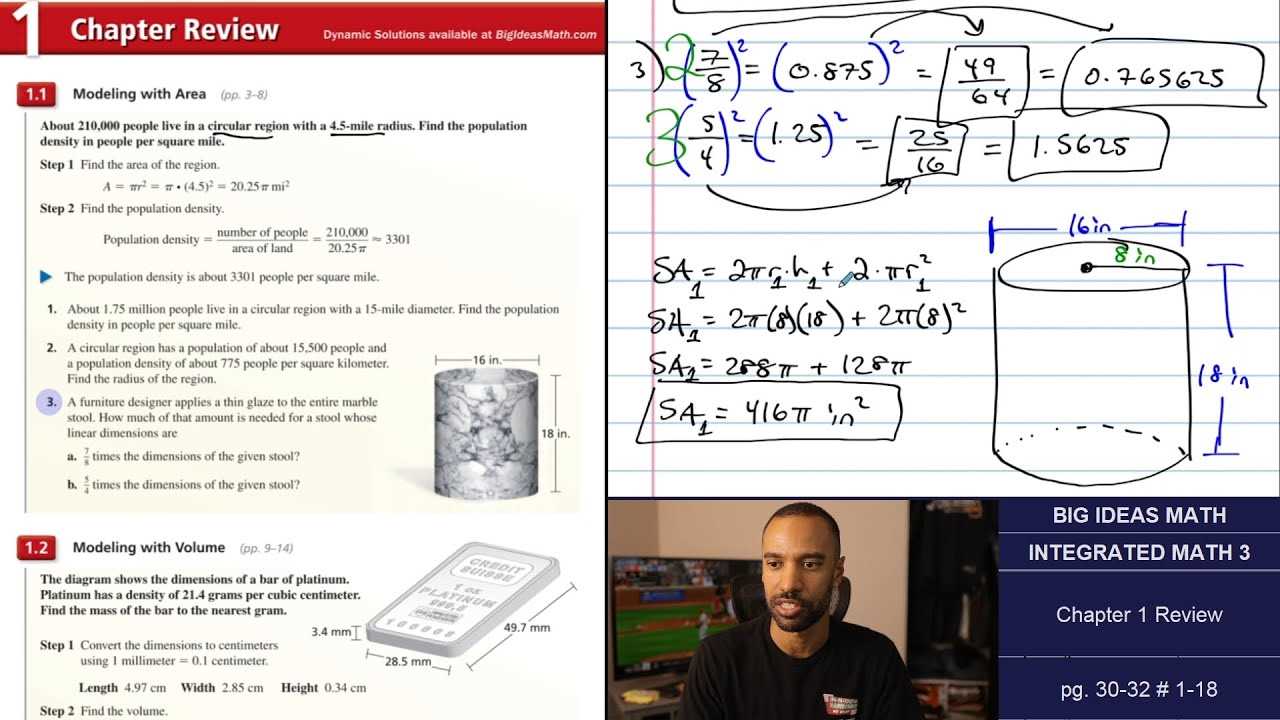
Extra practice is a vital part of mastering any subject. By working through additional exercises, students can reinforce their understanding and improve their problem-solving skills. Utilizing available tools effectively can provide the practice needed to enhance retention and gain confidence in tackling more complex problems.
Where to Find Extra Practice

There are various ways to access additional practice problems:
- Supplementary problem sets included in the materials.
- Online platforms offering interactive exercises.
- Books and workbooks with practice questions at various difficulty levels.
- Study groups or peer collaboration for tackling more challenging problems.
How to Maximize Practice Sessions
To get the most out of extra practice, follow these strategies:
- Start with easier problems and gradually increase the difficulty.
- Focus on areas where you feel less confident.
- After solving a problem, review the solution to ensure full understanding.
- Take breaks during long study sessions to avoid burnout and maintain focus.
How the Solution Guide Supports Learning

A solution guide plays a crucial role in the learning process by offering structured assistance when students face challenges. It helps clarify complex concepts and provides step-by-step explanations, allowing learners to understand the reasoning behind each solution. Rather than simply providing answers, the guide serves as a valuable teaching tool that enhances comprehension and critical thinking.
Clarifying Concepts and Methods
Each problem’s solution is presented with detailed explanations, breaking down the methods used to arrive at the answer. By following these steps, students can better understand the logic behind the solution and apply similar methods to other problems. This process encourages active learning, where students engage with the material to grasp both the “how” and the “why” behind each step.
Building Confidence and Independence
When learners encounter difficulties, the guide offers a way to check their work and gain confidence in their problem-solving abilities. Reviewing the steps in the guide reinforces understanding and encourages students to take ownership of their learning. Over time, this process helps build greater independence, as students become more capable of solving problems on their own without relying on immediate assistance.
Benefits of Chapter-by-Chapter Breakdown
Breaking down the learning material into smaller sections offers several advantages for students. By focusing on one segment at a time, learners can ensure that they fully grasp each concept before moving on to more advanced topics. This approach allows for better retention, a deeper understanding of the material, and greater confidence as students progress through the curriculum.
Each section is carefully structured to introduce new ideas in a logical sequence, providing a clear pathway for mastery. This method of learning ensures that students can identify and focus on areas that need improvement, while reinforcing concepts they’ve already learned.
| Benefits | How It Helps |
|---|---|
| Improved Focus | Breaking material into sections allows students to focus on one idea at a time, avoiding overwhelming them with too much information. |
| Better Retention | Smaller, more digestible sections help reinforce key concepts and improve memory retention over time. |
| Greater Understanding | By mastering one section before moving on, students gain a deeper understanding of each concept and how they connect to the next one. |
| Increased Confidence | Completing each section successfully builds students’ confidence, encouraging them to take on more difficult topics with a positive mindset. |
Common Mistakes to Avoid in Math
When tackling problems, even the most experienced learners can make certain errors that hinder progress. These mistakes, often made in the rush to find a solution, can be avoided with a bit more attention to detail. Recognizing these common pitfalls helps students stay focused and improve their problem-solving strategies.
One frequent mistake is misinterpreting the problem’s requirements. Often, learners rush into solving without fully understanding the question or the key information provided. Another common issue is making calculation errors, such as simple arithmetic mistakes or overlooking signs. Additionally, skipping steps in the process can lead to confusion and incorrect results.
To avoid these mistakes, take time to read through each problem carefully and check your work regularly. Double-checking calculations and ensuring that each step follows logically from the previous one can significantly reduce errors. Developing these habits not only improves accuracy but also builds confidence in solving future problems.
Exploring Additional Learning Resources

Expanding your learning beyond the core materials can enhance understanding and provide new perspectives on challenging concepts. By exploring various tools and platforms, students can strengthen their grasp of the subject matter and approach problems from different angles. These supplementary options can offer personalized support and reinforce what has been learned.
There are numerous ways to supplement your studies, including:
- Interactive online platforms offering exercises and tutorials.
- Video lessons that explain difficult concepts visually.
- Workbooks and additional printed materials for further practice.
- Collaborative study groups for discussing and solving problems together.
- Educational apps designed to provide instant feedback and track progress.
By incorporating these additional tools into your study routine, you can deepen your understanding and approach learning in a more comprehensive manner. With a combination of traditional resources and innovative methods, students can find the most effective strategies to succeed.
Improving Your Skills with the Answer Guide

To enhance your understanding of complex topics, it’s important to use available resources effectively. Reviewing solutions provides valuable insights into problem-solving techniques and helps identify areas for improvement. By analyzing the methods used to solve problems, you can adopt strategies that increase efficiency and accuracy in your own work.
Understanding the Process
Instead of simply looking at the final solutions, focus on understanding the steps involved in each problem. This will allow you to replicate the strategies in future problems, making your learning process more efficient. Break down each solution step-by-step, paying attention to the reasoning behind each action, which will help you avoid common errors.
Identifying Weak Areas

When you compare your solutions to those provided, note where your approaches differ. Identifying these discrepancies can highlight specific concepts or techniques that need more attention. This targeted focus will help you improve your overall skills by addressing problem areas directly and practicing more challenging questions.
How the Guide Helps with Problem Solving
A comprehensive guide can significantly enhance the problem-solving process by offering clear solutions and detailed explanations. It not only provides the correct answers but also outlines the steps needed to reach those conclusions, helping to strengthen logical reasoning and critical thinking skills. By studying the breakdown of each problem, students can learn to approach similar questions with confidence.
Here’s how such a guide supports effective problem solving:
- Clarifies Thought Process: Step-by-step instructions show how to methodically approach problems.
- Identifies Common Mistakes: Highlighting errors helps students avoid repeating them in the future.
- Boosts Confidence: Reviewing solutions builds self-assurance by reinforcing correct methods.
- Reinforces Key Concepts: Revisiting specific techniques strengthens the understanding of core principles.
- Provides Alternative Methods: It sometimes offers different ways of solving a problem, expanding problem-solving strategies.
By actively engaging with the guide, learners can develop a deeper understanding of the material and refine their problem-solving techniques. It becomes an essential tool for mastering complex topics and improving overall academic performance.
Accessing Digital Resources for Students
In today’s educational landscape, students have access to a variety of online tools that complement traditional learning methods. These digital platforms offer an array of interactive content, practice exercises, and instructional materials that can be accessed anytime, anywhere. They provide an excellent opportunity for students to enhance their understanding, reinforce lessons, and get additional support outside of regular classroom hours.
One of the main advantages of digital learning platforms is the ability to access personalized materials based on individual progress and needs. These resources are designed to cater to different learning styles, making the content more engaging and easier to absorb.
Types of Digital Materials Available
Digital platforms offer a broad range of materials that can assist students in their academic journey. Here are some of the most commonly available tools:
| Type of Resource | Description |
|---|---|
| Interactive Exercises | These exercises allow students to practice problems in real-time and receive immediate feedback on their performance. |
| Video Tutorials | Visual explanations of concepts help students grasp difficult topics more easily through step-by-step guides. |
| Practice Tests | Simulated assessments that mimic real exam conditions help students review and prepare for upcoming tests. |
| Supplementary Readings | Additional reading materials that provide in-depth explanations of key topics for students looking to dive deeper. |
By leveraging these digital tools, students can access materials that cater to their specific needs and learning pace. Whether for extra practice or to clarify complex concepts, these resources play a crucial role in supporting academic success.
Supporting Homework with Answer Key
Homework is a crucial part of the learning process, offering students the opportunity to practice and solidify what they’ve learned in class. However, students often encounter challenges when solving problems independently. This is where supplemental guides and solutions come into play. By providing clear explanations and solutions, these tools can greatly assist students in understanding their mistakes and learning from them.
The use of step-by-step guides can help students recognize where they went wrong and why certain methods or approaches yield the correct results. This promotes deeper understanding and encourages independent problem-solving in future assignments.
Benefits of Using a Solution Guide
Utilizing a comprehensive solution guide can provide several key benefits for students:
- Clarifies Mistakes: Students can pinpoint errors and adjust their approach accordingly.
- Enhances Understanding: By reviewing the detailed steps, students gain a better grasp of the underlying concepts.
- Boosts Confidence: Seeing the correct solutions helps students feel more confident in their abilities.
- Improves Time Management: Solution guides can assist in efficiently working through complex problems, saving time on difficult questions.
Effective Use of Solution Guides
To get the most out of solution guides, students should follow these best practices:
- Attempt the problem independently first, before checking the solution.
- Compare each step in the guide with your own work to identify any discrepancies.
- Take note of any alternative methods provided to solve the problem more efficiently.
- Use the solution as a learning tool, not just a quick fix.
By strategically using these guides, students can improve their problem-solving skills and become more self-sufficient learners.
How to Maximize Study Time

Efficient study habits are key to mastering any subject. By organizing your time effectively and focusing on important tasks, you can make the most of each study session. It’s not about the number of hours spent but how those hours are used. Smart planning, consistent effort, and effective techniques are the foundation for making your study time more productive and less stressful.
Key Strategies for Effective Study
To maximize the impact of your study sessions, it is essential to implement these proven techniques:
- Plan Ahead: Prioritize tasks based on importance and difficulty. This way, you can focus on areas where you need the most improvement.
- Set Specific Goals: Define clear objectives for each session. Whether it’s solving a set of problems or mastering a particular concept, goals help keep you on track.
- Use Active Learning: Engage with the material actively, through practice, self-testing, or explaining concepts to others, rather than passive reading.
- Stay Consistent: Consistent, smaller study blocks over time are more effective than cramming. Build a routine that fits your schedule.
- Take Breaks: Regular breaks help you stay refreshed and focused. The Pomodoro technique is a popular way to work in intervals, allowing for mental rest.
Sample Study Plan
Here is an example of how you might structure your study week to maximize productivity:
| Day | Focus Area | Duration |
|---|---|---|
| Monday | Review notes and summarize key concepts | 1.5 hours |
| Tuesday | Practice problems and quizzes | 2 hours |
| Wednesday | Study challenging material and rework mistakes | 2 hours |
| Thursday | Group study or collaborative learning | 1 hour |
| Friday | Review all material and test yourself | 1 hour |
By breaking your study time into focused blocks with clear goals, you ensure that each session is purposeful and efficient. This approach leads to more consistent progress and deeper understanding of the material.