In the field of statistics, analyzing relationships between different variables is crucial for drawing meaningful conclusions. One of the most common methods used in this process involves comparing observed data with expected values to assess patterns or deviations. This approach plays a significant role in making informed decisions based on statistical evidence, whether in research, experiments, or real-life applications.
For students and practitioners alike, mastering this technique requires a deep understanding of the underlying concepts and a step-by-step approach to solving problems. With the right tools, anyone can enhance their ability to perform complex analyses and interpret results accurately. This guide offers a structured method to help navigate through statistical challenges, providing clarity and insight into each phase of the problem-solving process.
Chi Square POGIL Answer Key Overview
In statistics, problem-solving exercises often require a systematic approach to analyze data and assess the validity of certain hypotheses. The process involves using specific methods to compare expected and observed frequencies, allowing for conclusions to be drawn based on the results. A structured guide through this process can significantly enhance understanding, providing step-by-step assistance for students and learners.
Understanding the Structure of the Exercise
These exercises are designed to guide individuals through various stages of data analysis, emphasizing key concepts such as hypothesis testing, expected values, and statistical significance. By following a logical sequence, learners are equipped to identify patterns, make informed decisions, and correctly interpret statistical outcomes. A detailed overview of each step ensures a comprehensive grasp of the method, making complex problems more approachable.
Application and Benefits of the Method
Applying this method to real-life scenarios helps solidify theoretical knowledge and fosters a deeper understanding of statistical principles. It empowers learners to tackle a range of problems with confidence, whether in academic settings or practical applications. The structured approach not only enhances problem-solving skills but also ensures accuracy in analyzing data and deriving conclusions.
Understanding the Basics of Chi Square
At the heart of many statistical analyses is the concept of comparing observed data with expected values to determine whether there are significant differences. This technique is essential for evaluating the strength of relationships between variables and understanding if a hypothesis holds true. It is a fundamental method that helps uncover patterns in data, allowing for more informed decisions in both academic and real-world contexts.
In its simplest form, the method involves calculating a statistic that measures the difference between observed frequencies and the frequencies that would be expected under a specific hypothesis. If the observed and expected values diverge significantly, it suggests that the hypothesis may need to be reevaluated. Understanding how to properly conduct these tests and interpret the results is crucial for drawing valid conclusions from data.
What is POGIL and Its Role
Active learning strategies are essential for helping individuals deeply engage with and understand complex concepts. One such approach focuses on guiding learners through collaborative activities that encourage exploration, critical thinking, and problem-solving. This method not only helps participants absorb key ideas but also equips them with the skills needed to apply knowledge in practical contexts.
In the context of statistics and data analysis, this approach provides structured exercises that lead learners through the process of hypothesis testing, helping them apply theoretical knowledge to real-world problems. The role of this method is to create an interactive learning environment where learners can gain a hands-on understanding of statistical principles, collaborate with others, and strengthen their analytical thinking skills.
| Benefits | Description |
|---|---|
| Enhanced Understanding | Provides learners with a deeper grasp of complex concepts through hands-on application. |
| Critical Thinking | Encourages learners to think critically and analyze data beyond surface-level observations. |
| Collaboration | Promotes teamwork, allowing students to learn from one another and refine their problem-solving skills. |
Step-by-Step Guide to Chi Square
When analyzing data to determine if there are significant differences between observed and expected outcomes, a methodical approach is essential. This process involves several stages, from calculating expected values to interpreting the results. By following a structured guide, individuals can ensure accuracy and improve their understanding of statistical testing.
Step 1: Define the Hypothesis
Start by clearly stating the null hypothesis, which assumes no significant difference between the observed and expected frequencies. The alternative hypothesis suggests that a notable difference exists. This is the foundation for performing the test and guides the entire process.
Step 2: Collect and Organize Data
Gather the observed frequencies and arrange them in a contingency table. For each category or variable, list the counts of occurrences. Next, calculate the expected frequencies for each category based on the assumption that the null hypothesis holds true.
Ensure the data is complete and well-organized, as this will affect the accuracy of your calculations. Once you have the observed and expected values, you can proceed to calculate the test statistic and assess the results.
Key Concepts in Chi Square Analysis
To perform a meaningful statistical test, it’s crucial to understand the fundamental concepts that drive the analysis process. The key principles involve comparing observed data to what would be expected if there were no effect or relationship between variables. Grasping these concepts ensures accurate interpretation and application of the test in various scenarios.
Understanding the Test Statistic
The test statistic is central to this analysis. It measures the difference between the observed and expected frequencies, helping to determine whether the discrepancies are large enough to suggest a significant relationship. This statistic is used to calculate the probability, or p-value, that indicates whether the result is due to chance or reflects a true effect.
Critical Concepts to Remember
- Null Hypothesis: The assumption that there is no significant difference between observed and expected frequencies.
- Expected Frequencies: The values that are predicted based on the assumption that the null hypothesis is true.
- Degrees of Freedom: A parameter that adjusts the calculation based on the number of categories or groups in the dataset.
- P-Value: The probability that the observed differences occurred by random chance. A small p-value suggests a significant result.
- Significance Level: The threshold (usually 0.05) used to determine whether the p-value is small enough to reject the null hypothesis.
Mastering these concepts is essential for performing accurate statistical analyses and drawing reliable conclusions from data. They form the backbone of the decision-making process, guiding the interpretation of results and the understanding of statistical tests.
How to Approach POGIL Exercises
Engaging with interactive learning activities is a valuable way to deepen understanding of complex concepts. The exercises are designed to guide learners through the process of problem-solving, encouraging them to work step by step and think critically. The goal is to build knowledge progressively, providing a structured approach to mastering statistical methods.
When approaching these exercises, it is essential to remain focused on the overall objective: to explore the relationships between observed and expected values and to evaluate the strength of those relationships. This requires careful attention to detail, as well as the ability to follow the sequence of tasks and apply relevant formulas at the right stages of the exercise.
Steps to follow:
- Read the instructions carefully: Make sure to understand the context and the goals of the exercise before beginning.
- Identify the key data: Pay close attention to the values provided in the exercise and organize them for analysis.
- Follow the logical sequence: Tackle each task one at a time, ensuring that you complete each step thoroughly before moving on.
- Collaborate and discuss: Engage with peers or mentors when necessary, as collaboration can help clarify concepts and improve understanding.
- Review your results: Once the exercise is completed, double-check your calculations and interpretations to ensure accuracy.
By approaching these activities with a systematic mindset, you will not only develop a deeper understanding of statistical analysis but also gain valuable problem-solving skills that can be applied to a wide range of topics.
Importance of Statistical Significance
In data analysis, determining whether the results of an experiment or study are meaningful requires evaluating their statistical significance. This concept helps to distinguish between outcomes that are likely due to random chance and those that reflect a true underlying pattern or effect. Without understanding statistical significance, it becomes difficult to draw reliable conclusions from data.
Why Statistical Significance Matters

Statistical significance provides a framework for understanding whether the observed differences or relationships in the data are likely to be genuine. A result is considered statistically significant if it is unlikely to have occurred by chance alone, given a predefined threshold. This allows researchers and analysts to make informed decisions, rather than relying on assumptions or subjective interpretation.
Impact on Decision-Making
Accurate interpretation of statistical significance directly influences the quality of decisions made based on data. In fields such as medicine, economics, and social sciences, understanding whether a result is significant ensures that policies, treatments, and conclusions are grounded in valid evidence. Without this step, decisions may be based on random fluctuations or untrustworthy patterns.
Common Mistakes in Chi Square Problems
When working with statistical tests that compare observed and expected frequencies, there are several common pitfalls that can lead to incorrect conclusions. These errors can arise from misunderstandings of the method, miscalculations, or even improper interpretation of results. Being aware of these mistakes is essential for ensuring the accuracy and reliability of your analysis.
1. Incorrect Calculation of Expected Values
One of the most frequent mistakes in this type of analysis is failing to calculate expected frequencies correctly. These values are crucial for the test and must be based on the assumption that the null hypothesis is true. Mistakes in setting up the formula or misinterpreting the dataset can result in inaccurate expected values, leading to flawed conclusions.
2. Ignoring Assumptions of the Test

Every statistical test, including this one, operates under certain assumptions, such as the independence of observations and the need for sufficiently large sample sizes. Ignoring these assumptions or not verifying them beforehand can undermine the validity of the results. In particular, small sample sizes or dependent data can distort the test statistic and lead to misleading findings.
Interpreting Chi Square Results Correctly
Accurately interpreting the results of statistical tests is essential for drawing valid conclusions. After calculating the test statistic, the next crucial step is determining whether the results suggest a meaningful relationship between the variables or if the observed differences are likely due to random variation. Understanding the outcome requires careful analysis of the test statistic, p-value, and degrees of freedom.
Understanding the P-Value
The p-value is a key indicator in determining whether the observed data deviates significantly from what would be expected under the null hypothesis. A small p-value (typically below 0.05) indicates that the result is unlikely to have occurred by chance, suggesting that the observed differences are statistically significant. On the other hand, a large p-value suggests that there is insufficient evidence to reject the null hypothesis, meaning the observed differences are likely due to random variation.
Evaluating the Test Statistic and Degrees of Freedom
The test statistic quantifies the difference between observed and expected values. It is essential to compare this statistic to a critical value based on the degrees of freedom, which depend on the number of categories in the data. If the test statistic exceeds the critical value, it indicates that the differences between observed and expected frequencies are significant, leading to the rejection of the null hypothesis.
By correctly interpreting both the p-value and test statistic, you can confidently assess the strength of the evidence and determine whether a meaningful relationship exists between the variables being studied.
Using the Chi Square Formula
The formula for this statistical test is essential for comparing observed frequencies with expected frequencies to determine if there is a significant difference between them. The formula provides a systematic approach to calculating a test statistic that can then be compared to a critical value to assess the null hypothesis. Understanding how to apply this formula correctly is crucial for obtaining reliable results from the analysis.
The Formula Breakdown
The formula involves summing the squared differences between the observed and expected frequencies, divided by the expected frequencies for each category. Mathematically, it is expressed as:
Test Statistic = Σ ( (Observed – Expected)² / Expected )
Where:
- Observed: The actual data values that have been collected.
- Expected: The values that would be expected based on the assumption of no effect or relationship.
- Σ: The summation symbol, which indicates that the calculation must be performed for each category and then summed up.
Steps to Apply the Formula
- Step 1: Gather the observed data values from your dataset.
- Step 2: Calculate the expected values based on the assumption of no relationship.
- Step 3: Apply the formula to each category by subtracting the expected value from the observed value, squaring the result, and dividing by the expected value.
- Step 4: Sum all the values to get the test statistic.
Once you have calculated the test statistic, it can be compared to the critical value based on the degrees of freedom to determine if the result is statistically significant.
When to Use Chi Square Test
This statistical method is used when you need to assess whether there is a significant association between two categorical variables. It helps to determine if the differences between observed and expected frequencies are large enough to suggest a real relationship, or if they could be attributed to random variation. It’s particularly useful when dealing with data that is divided into distinct categories or groups.
The test is appropriate in scenarios where you are comparing frequencies across different categories, such as determining if the distribution of responses in a survey matches expected patterns, or if there is a relationship between two categorical variables like gender and voting preference. It’s also commonly used for contingency table analysis, where the data is organized in a matrix format showing the frequency of observations for different combinations of categories.
It is important to note that the test assumes the observations are independent, the sample size is sufficiently large, and the expected frequency for each category is not too low, typically at least five. If these conditions are met, the test provides a powerful tool for understanding patterns and relationships within categorical data.
Advanced Topics in Chi Square Testing
While the basic application of this statistical method is crucial for analyzing categorical data, there are several advanced topics and techniques that can further enhance its utility and precision. These topics are particularly relevant when dealing with more complex datasets or when seeking a deeper understanding of the relationships between variables. Below are some advanced considerations that can be important when conducting more sophisticated analyses.
1. Dealing with Small Sample Sizes
One of the key challenges when applying this test is handling small sample sizes. The reliability of the results diminishes when expected frequencies are low, typically less than five. In such cases, the test might not provide accurate conclusions. Alternatives and solutions include:
- Fisher’s Exact Test: Useful when sample sizes are small, especially in 2×2 tables.
- Yates’ Continuity Correction: Adjusts the test to be more appropriate for small samples, reducing the risk of Type I errors.
- Combining Categories: Grouping similar categories can help ensure that each expected frequency is large enough to meet the test’s assumptions.
2. Applying the Test to More Complex Tables
When dealing with contingency tables larger than 2×2, the complexity of interpreting results increases. However, this test can still be applied to larger tables by using:
- Multivariate Analysis: In cases where more than two variables are involved, a multivariate analysis can be employed to examine the relationship between multiple categorical variables simultaneously.
- Adjusted Standardized Residuals: These can be used to detect which cells in a large table contribute the most to the overall test statistic.
3. Goodness of Fit vs. Test of Independence
While both types of tests involve comparing observed and expected frequencies, there are important differences in their use:
- Goodness of Fit: This test is used to determine if a sample data matches a specific distribution or pattern.
- Test of Independence: This type of test evaluates whether two categorical variables are independent or if there is a relationship between them.
Both methods are essential tools in categorical data analysis, but selecting the right one depends on the nature of the hypothesis and the structure of the data.
Common Misconceptions About Chi Square
Despite its widespread use in statistical analysis, there are several common misconceptions about this method that can lead to misinterpretation of results. These misunderstandings often arise from a lack of clarity about its assumptions, applications, and limitations. Below are some of the most frequently held misconceptions:
1. The Test Can Be Used for Any Type of Data
One common misconception is that this statistical method can be applied to any type of data, regardless of its nature. However, this test is specifically designed for categorical data. It is not appropriate for continuous data, which must be transformed or treated using different techniques. Some key points to remember include:
- Categorical Data: The test requires data that can be categorized into distinct groups, such as “yes” or “no”, “male” or “female”, etc.
- Continuous Data: For continuous variables (e.g., height, weight, temperature), alternative statistical methods such as t-tests or regression analysis should be used.
2. A Higher Test Statistic Always Means a Stronger Relationship
Another misconception is that a higher test statistic automatically indicates a stronger or more significant relationship between variables. In reality, the test statistic only measures the difference between observed and expected frequencies, but it must be considered alongside the p-value. A large statistic without statistical significance (high p-value) may still indicate a random fluctuation rather than a true relationship. Key points to consider:
- Test Statistic: While a large test statistic suggests a larger deviation, the significance depends on the p-value.
- P-Value: A small p-value (typically less than 0.05) indicates statistical significance, while a larger p-value suggests no significant relationship.
3. The Test Requires Large Sample Sizes
Many people assume that this method can only be used with large sample sizes. While larger samples provide more reliable results, this test can be applied to smaller datasets, as long as the expected frequencies are not too low. Misconceptions about sample size limitations can often lead to incorrect conclusions. Here’s what to keep in mind:
- Sample Size: Small sample sizes can be problematic if they result in low expected frequencies, but tests like Fisher’s Exact Test can be used instead.
- Expected Frequency: Ensure that expected frequencies are sufficiently large (typically at least 5) to avoid inaccurate results.
4. It Can Prove Causation
Some individuals believe that this statistical test can demonstrate causality between variables. However, this test only assesses the association between two categorical variables; it does not imply that one variable causes the other. To infer causality, a different research design, such as an experimental study or longitudinal analysis, is required. Key distinctions to remember:
- Association vs. Causation: The test shows if a relationship exists but does not establish a cause-and-effect link.
- Further Investigation: To prove causality, further experiments or additional statistical methods, such as regression analysis, must be employed.
5. The Data Must Always Be Normally Distributed
Unlike many other statistical tests, this method does not require the data to be normally distributed. This misconception arises because many statistical tests rely on normality assumptions. In contrast, this test evaluates categorical data, which does not require a normal distribution. However, other assumptions such as sample size and independence of observations should still be met for the test to be valid.
How to Verify Your Chi Square Solution
After completing a statistical analysis using this method, it is essential to verify that the solution is accurate and reliable. Verification ensures that no errors were made during the calculation and that the results can be confidently interpreted. The following steps provide a comprehensive approach to confirming the correctness of your solution.
1. Check the Data Assumptions
Before diving into the results, it’s crucial to verify that the assumptions for the analysis were met. These assumptions include:
- Categorical Data: Ensure that the variables analyzed are indeed categorical and not continuous.
- Independence: Confirm that the observations are independent of each other, meaning that one observation does not influence another.
- Expected Frequencies: Check that all expected frequencies are sufficiently large, typically greater than 5, to avoid inaccuracies in the results.
2. Recalculate the Test Statistic
Recalculate the test statistic to confirm that the values you derived are correct. The general formula involves comparing observed and expected frequencies for each category, and the formula should be followed precisely. Here’s a simple formula breakdown:
| Observed Frequency | Expected Frequency | Formula |
|---|---|---|
| O | E | (O – E)2 / E |
Sum the results for each category to get the final test statistic. If the statistic does not align with the one calculated previously, there may have been an error in your calculations.
3. Double-Check the Degrees of Freedom
The degrees of freedom (df) play a significant role in determining the critical value for your test. Verify that you calculated the correct degrees of freedom, which is typically computed as:
- df = (number of rows – 1) * (number of columns – 1)
Incorrect degrees of freedom can lead to the wrong critical value and ultimately affect the interpretation of your results.
4. Compare with the Critical Value
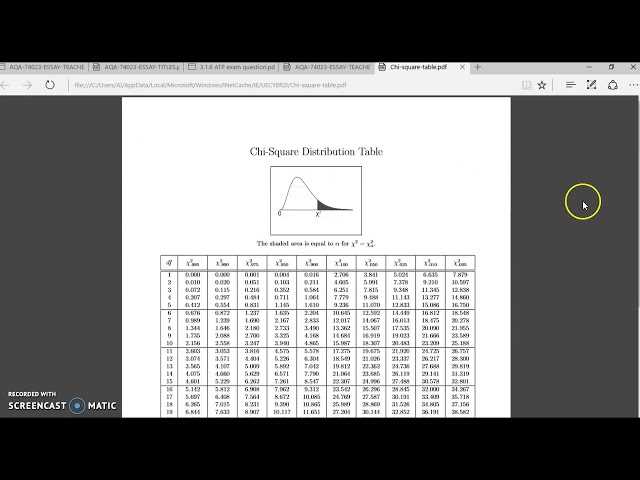
Once the test statistic and degrees of freedom are confirmed, compare the calculated test statistic with the critical value from the chi-square distribution table. If the test statistic exceeds the critical value, the null hypothesis is rejected. If not, you fail to reject the null hypothesis. Ensure that you are using the correct significance level (typically 0.05) for your comparison.
5. Verify the P-Value
Finally, verify the p-value associated with the test statistic. The p-value indicates the probability of observing a test statistic as extreme as, or more extreme than, the one calculated. If the p-value is less than the significance level, the results are considered statistically significant. Make sure the p-value is consistent with the test statistic and degrees of freedom.
Real-World Applications of Chi Square
Statistical methods play a crucial role in understanding and interpreting data across a wide range of fields. One such method is used to determine whether there is a significant association between categorical variables. This technique is widely applied in various real-world situations to test hypotheses and make data-driven decisions. Below are some key examples of its application in different sectors.
1. Medical Research

In healthcare, researchers often use this statistical method to analyze the relationship between different factors, such as lifestyle choices and the incidence of disease. For example, researchers might want to know if there is a link between smoking and lung cancer among different age groups. This method helps to assess whether the distribution of cases deviates significantly from what would be expected by chance.
2. Marketing and Consumer Behavior
Businesses frequently apply this technique to understand consumer preferences and behaviors. For instance, a company might conduct surveys to see if there is a correlation between age groups and preferred product features. By using this statistical test, they can determine whether the distribution of responses differs from expected patterns based on a random selection.
3. Education and Testing
In educational settings, this method is often used to analyze exam results. For example, an educator might use it to compare how different teaching methods affect student performance across various demographic groups. This can help identify whether any observed differences in scores are statistically significant or simply due to random variation.
4. Social Sciences and Survey Analysis
Researchers in the social sciences frequently use this technique to assess the relationship between variables in survey data. For instance, it can be used to examine whether there is a significant difference in voting behavior based on gender or ethnicity. Such analyses help policymakers and social scientists understand patterns in society and guide informed decision-making.
5. Environmental Studies
Environmental scientists can also apply this statistical test to assess the impact of certain environmental factors on wildlife populations. For instance, they might study the effects of pollution on the number of a specific species in different regions. The results of such tests can provide insights into the extent of the environmental impact and inform conservation efforts.
Example Table: Medical Research on Smoking and Lung Cancer

| Age Group | Smokers (Observed) | Non-Smokers (Observed) | Expected Smokers | Expected Non-Smokers |
|---|---|---|---|---|
| 18-25 | 100 | 50 | 80 | 70 |
| 26-40 | 150 | 100 | 130 | 120 |
| 41-60 | 200 | 150 | 190 | 160 |
| 61+ | 80 | 120 | 100 | 100 |
In this example, the table shows observed and expected frequencies of smokers and non-smokers in various age groups. Statistical analysis would help determine if there is a significant association between smoking and age group.
Final Tips for Solving Chi Square Problems
When approaching statistical problems involving categorical data, it’s essential to follow a systematic approach. By adhering to a clear step-by-step method, you can accurately interpret results and avoid common pitfalls. Below are some crucial tips that will help ensure the accuracy and efficiency of your analysis.
- Double-Check Your Data: Before you begin any calculations, make sure your data is organized and categorized correctly. Incorrect classification of variables can lead to inaccurate results.
- Calculate Expected Frequencies Properly: One of the most important steps is to determine the expected frequencies. Ensure you use the correct formula to compute these values, taking into account the total sample size and the distribution of categories.
- Verify Assumptions: The method relies on certain assumptions, such as the independence of observations and sufficiently large sample sizes. Make sure your data meets these assumptions before proceeding with the analysis.
- Use a Good Significance Level: The choice of significance level (usually 0.05) is critical when evaluating the p-value. A common mistake is to use an inappropriate significance level, which could lead to incorrect conclusions.
- Look for Significant Differences: After performing the calculation, compare the test statistic to the critical value from the relevant distribution table. If the statistic exceeds the critical value, you can reject the null hypothesis, suggesting a significant association between the variables.
- Understand the Limitations: Statistical tests are not perfect. Even if the results suggest a significant association, remember that correlation does not imply causation. Always consider other factors and conduct further research if necessary.
- Practice Makes Perfect: The best way to master this technique is through practice. Work through various problems to build your understanding and speed, ensuring you are comfortable with the steps involved.
By following these steps and tips, you can confidently approach problems and improve the accuracy of your statistical analyses. Remember, a systematic and thoughtful approach is key to success in any data-driven problem-solving task.