Common Core Algebra 1 Unit 1 Answer Key

Mathematics can often be a challenging subject for many students, especially when it comes to solving foundational problems. Mastering basic concepts and strategies is essential for building confidence and improving problem-solving skills. This section focuses on providing clear solutions to common problems that arise in early-level math courses, helping students grasp the essential techniques they need for success.

Step-by-step guidance through typical exercises helps demystify difficult topics. By reviewing how to approach basic equations, expressions, and mathematical operations, learners can enhance their understanding and prepare for more advanced material. The solutions provided offer clarity and support, allowing students to self-assess their progress and identify areas that need further attention.

Whether you are reviewing material for the first time or reinforcing your knowledge, this resource will serve as a helpful tool for strengthening your math skills. With a focus on practical application and clear examples, students can make steady improvements and achieve a deeper comprehension of the subject.

Common Core Algebra 1 Unit 1 Answer Key

When working through the initial steps of math problem-solving, understanding the solutions to foundational exercises is essential. This section provides a guide to help students verify their methods and ensure they are on the right track. By closely reviewing the calculations and logical steps involved in solving problems, learners can build a strong foundation for tackling more complex challenges ahead.

Here, you’ll find detailed solutions that clarify common exercises typically encountered at the start of math courses. The explanations aim to show how each step is connected, demonstrating the best approach to solving basic equations and simplifying expressions.

• Step-by-step breakdowns: Each problem is addressed with a detailed explanation of the process used to reach the correct solution.
• Practice exercises: A series of typical problems is included, so you can compare your solutions with the provided answers.
• Highlighting key concepts: Important ideas like order of operations, variable manipulation, and equation solving are clearly explained throughout the section.
• Self-checking tips: Guidance on how to check your own work ensures accuracy and helps reinforce learning.

By reviewing these solutions, students will gain a better understanding of how to approach math problems effectively. Repetition and practice are key to mastering the concepts, and this resource serves as a valuable tool for reinforcing that knowledge.

Understanding the Basics of Algebra 1

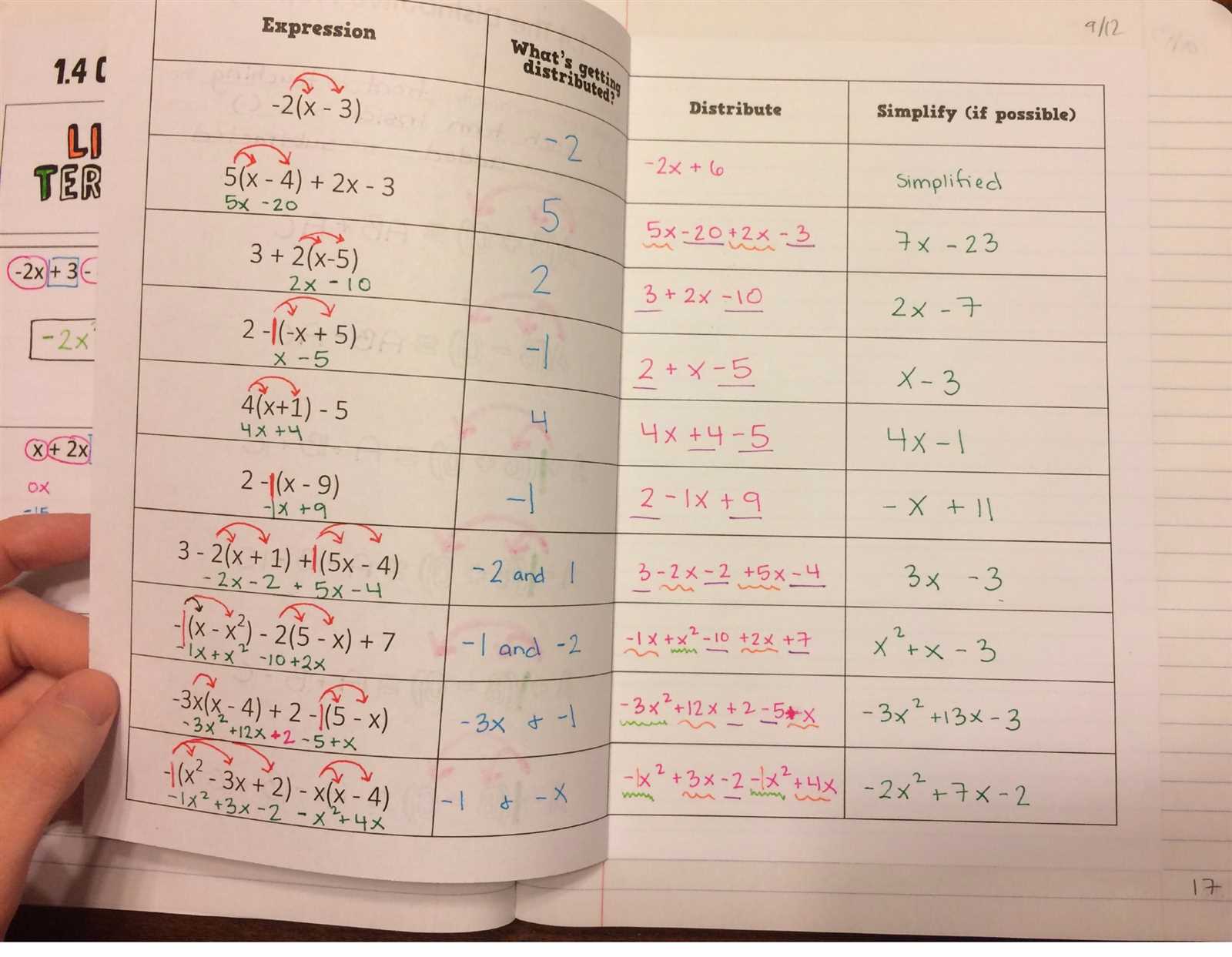
Mastering the foundational concepts of mathematics is crucial for progressing through more complex topics. The primary focus in the early stages is to become comfortable with working with numbers, variables, and equations. These skills serve as the building blocks for higher-level problem-solving and mathematical reasoning. By understanding how to manipulate expressions and solve for unknown values, students gain the confidence needed to tackle more advanced concepts.

One of the first areas of focus involves understanding how to work with basic operations, such as addition, subtraction, multiplication, and division, when applied to variables and numbers. It’s also essential to grasp the relationship between different elements within an equation, and how manipulating one part can affect the overall solution. Clear comprehension of these simple principles sets the stage for mastering more difficult problems in later stages of learning.

With practice and consistent application of these principles, learners will develop the necessary skills to approach problems with greater ease and accuracy. This section aims to break down key topics into manageable steps, making it easier to understand the logic behind each calculation and why each step is essential in reaching the final solution.

Key Concepts in Unit 1 Algebra

In the initial stages of any mathematics course, understanding the foundational principles is essential for building a solid base. The first set of concepts focuses on how to manipulate variables, expressions, and simple equations. Mastering these ideas allows students to progress smoothly and tackle increasingly complex problems. The emphasis is on clarity, logic, and applying basic operations to real-world scenarios.

Working with Variables and Expressions

One of the primary focuses in the early lessons is learning how to handle variables within expressions. A variable represents an unknown value, and understanding how to manipulate these variables is crucial for solving equations. Students are introduced to writing and simplifying expressions, which involve using arithmetic operations on variables and constants. Developing comfort with variables sets the stage for more advanced topics, such as solving equations and inequalities.

Solving Simple Equations

The next important concept involves solving equations, which requires finding the value of a variable that satisfies the equation. This involves balancing both sides of an equation by applying inverse operations. Students begin by solving simple linear equations and gradually work up to more complex forms. The process teaches critical thinking and problem-solving skills that are essential throughout the entire study of mathematics.

How to Use the Answer Key Effectively

Using a solution guide is an essential part of the learning process, helping students verify their results and understand the reasoning behind each step. The key is not just to check the final answer but to understand the methods used to reach it. This approach ensures that learners can identify mistakes, correct them, and apply the correct strategies in future exercises.

Step-by-Step Review

Instead of simply comparing answers, take the time to go through each solution step by step. Focus on the operations and logic used to solve each problem. By breaking down the process, you can identify areas where you might have gone wrong and improve your understanding of the method. This review is crucial for reinforcing concepts and improving problem-solving skills.

Self-Assessment and Progress Tracking

Use the solution guide to assess your current understanding. After solving a problem, check if your approach matches the one in the guide. If discrepancies arise, try to solve the problem again, focusing on the areas where mistakes were made. This method not only helps to correct errors but also serves as a valuable tool for tracking progress over time.

Step-by-Step Solutions for Common Problems

Breaking down problems into smaller, manageable steps is one of the most effective ways to ensure accuracy and understanding. When facing typical challenges in basic mathematical tasks, it’s important to approach them methodically, focusing on one step at a time. This section will provide a detailed guide to solving frequent problems, allowing students to grasp the logic behind each calculation and apply similar methods to other exercises.

Step	Description	Example
Step 1	Identify the given values and what needs to be solved.	For the equation 2x + 5 = 11, identify that you need to solve for x.
Step 2	Isolate the variable by performing inverse operations.	Subtract 5 from both sides of the equation: 2x = 6.
Step 3	Solve for the variable by simplifying the equation further.	Divide both sides by 2: x = 3.
Step 4	Check the solution by substituting the value back into the original equation.	Substitute x = 3 back into 2x + 5 = 11: 2(3) + 5 = 11, which is true.

By following these steps, you can solve most basic problems systematically and efficiently. Whether working with simple equations or more complex expressions, this method ensures clarity and reduces the chance of making mistakes along the way.

Common Mistakes in Algebra 1 and How to Avoid Them

In any math course, it’s easy to make simple errors that can lead to incorrect results. Recognizing these mistakes and learning how to avoid them is crucial for improving your understanding and accuracy. This section highlights some of the most frequent pitfalls students encounter and offers strategies to ensure correct solutions.

• Incorrect Order of Operations: One of the most common errors is neglecting the correct sequence of operations. Always remember to follow PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). A mistake here can lead to drastically different results.
• Misinterpreting Variables: Students often confuse the meaning of variables or forget that a letter represents an unknown value. Take care to treat each variable separately and understand that it can take on different values depending on the equation.
• Sign Errors: Forgetting to change signs when adding or subtracting negative numbers is a frequent mistake. Always double-check signs when performing operations involving negative values to avoid this error.
• Skipping Steps: Many students rush through problems and skip steps, leading to mistakes in solving equations. Always take the time to show each step clearly and avoid jumping ahead.
• Incorrect Distribution: Failing to correctly apply the distributive property is another common mistake. When multiplying a term by an expression in parentheses, ensure that you distribute the multiplication to each term inside the parentheses.

By being aware of these errors and taking the necessary precautions, students can improve their accuracy and build a stronger foundation in mathematics. Practice, patience, and a careful approach are key to avoiding mistakes and mastering fundamental concepts.

Understanding the Order of Operations

In mathematics, performing calculations in the correct sequence is essential for obtaining accurate results. The order in which operations are carried out determines the outcome of an expression. Without a clear understanding of this sequence, even simple problems can lead to incorrect answers. This section explores the importance of following the right order when solving mathematical expressions.

The Rules for Proper Sequence

The sequence of operations is typically governed by a specific rule set. To ensure clarity and consistency, mathematicians follow the acronym PEMDAS, which stands for:

• Parentheses: Perform calculations inside parentheses first.
• Exponents: Solve powers and square roots next.
• Multiplication and Division: These operations are performed from left to right.
• Addition and Subtraction: Lastly, solve these from left to right.

Why Following the Order Matters

Skipping steps or misapplying the order can lead to drastic errors, especially as problems grow more complex. For example, the expression 3 + 5 × 2 should be solved by first multiplying 5 and 2 (giving 10), then adding 3 (resulting in 13). If the addition is done first, the result would be incorrect. Always remember to follow the steps precisely to avoid confusion and ensure accurate solutions.

Exploring Variables and Expressions

Understanding how to work with unknown values and mathematical statements is fundamental to solving equations and performing calculations. Variables and expressions serve as the building blocks for more complex problems. In this section, we will explore what variables represent and how to manipulate expressions involving them.

The Role of Variables

A variable is a symbol, usually a letter, that represents an unknown value. These placeholders allow us to work with general relationships and solve problems where specific numbers are not yet known. Here are some key points about variables:

• Representation: Variables are used to represent unknown quantities in an equation or expression.
• Flexibility: The value of a variable can change depending on the context of the problem.
• Substitution: Once the value of a variable is determined, it can be replaced with a specific number.

Working with Expressions

An expression is a combination of numbers, variables, and operators (such as addition, subtraction, multiplication, and division). Here’s how to approach working with expressions:

1. Simplification: Combine like terms by adding or subtracting them.
2. Substitution: Substitute known values for the variables to evaluate the expression.
3. Expansion: Apply distributive properties to expand expressions when necessary.

Mastering variables and expressions is essential for solving more complex equations and understanding mathematical relationships. By practicing these concepts, you’ll be able to approach problems with confidence and accuracy.

Solving Simple Equations Explained

Solving equations is one of the fundamental skills in mathematics. It involves finding the value of an unknown variable that makes a given mathematical statement true. In this section, we will walk through the process of solving simple equations, focusing on step-by-step methods that can be applied to a variety of problems.

Understanding the Process

To solve an equation, the goal is to isolate the variable on one side of the equation. This can be achieved by performing inverse operations, which “undo” the operations applied to the variable. The key steps typically include:

• Identify the variable: The first step is to determine which symbol represents the unknown value.
• Apply inverse operations: Use the opposite operations (addition, subtraction, multiplication, division) to move other terms away from the variable.
• Isolate the variable: Continue applying operations until the variable is alone on one side of the equation.

Example: Solving a Basic Equation

Consider the equation:

2x + 5 = 11

Here’s how you would solve it:

1. Start by subtracting 5 from both sides to eliminate the constant on the left side:

2x = 6

2. Next, divide both sides by 2 to isolate the variable:

x = 3

Thus, the solution to the equation is x = 3.

By practicing these steps and applying them consistently, solving equations will become more intuitive and easier to manage. Keep in mind that while this is a simple example, the same approach applies to more complex equations as well.

Using the Answer Key for Self-Assessment

Evaluating your own progress in solving mathematical problems is essential for understanding concepts deeply and improving your skills. Using a solution guide can be a powerful tool for self-assessment, allowing you to check your work, identify mistakes, and reinforce your understanding of key concepts. This section discusses how to effectively use a solution guide to monitor and improve your progress.

Steps for Effective Self-Assessment

Follow these steps to make the most of a solution guide:

1. Compare Your Work: After solving a problem, compare your solution with the provided guide. Pay attention to each step to see if you followed the correct process.
2. Identify Mistakes: If your solution differs from the one in the guide, carefully review the steps where you went wrong. This helps pinpoint areas that need improvement.
3. Understand the Correct Method: If a mistake is made, focus on understanding why the correct method works. This deeper understanding will prevent similar errors in the future.
4. Practice Similar Problems: Use the guide to practice similar problems. Reinforcing your knowledge with repeated practice helps solidify concepts and builds confidence.

Using Solutions for Continuous Improvement

Self-assessment with a solution guide should not only focus on identifying errors but also on improving the approach. By revisiting problems where you made mistakes and using the solutions to refine your methods, you create a continuous learning loop. Regular practice and self-assessment will enhance both your accuracy and problem-solving speed over time.

Remember, the goal of using a solution guide is not just to check if you got the right answer but to understand the process that leads to the correct solution. This will help you become more confident and proficient in solving future problems.

How to Approach Word Problems

Word problems often pose a challenge for many students, as they require translating real-world situations into mathematical equations. The key to solving these problems lies in breaking down the information step by step and identifying the relationships between the given quantities. This section will explore effective strategies for approaching and solving word problems efficiently.

Step-by-Step Strategy for Solving Word Problems

Follow this approach to tackle word problems with confidence:

1. Read Carefully: Read the problem several times to ensure you understand all the details. Pay attention to the numbers, keywords, and what the problem is asking.
2. Identify Variables: Assign variables to the unknown quantities. This step helps you represent the problem mathematically.
3. Translate to an Equation: Use the relationships described in the problem to form an equation. Look for keywords that indicate operations like addition, subtraction, multiplication, or division.
4. Solve the Equation: Apply appropriate mathematical methods to solve for the unknown variable. Be sure to follow the correct order of operations as needed.
5. Interpret the Solution: Once you have solved for the variable, make sure your answer makes sense in the context of the problem. If necessary, check the solution by plugging it back into the original scenario.

Common Pitfalls to Avoid

Word problems often include tricky wording or additional information that can be distracting. Keep these tips in mind to avoid common mistakes:

• Misinterpreting Keywords: Ensure you understand what each term in the problem refers to, such as “total,” “difference,” “product,” or “sum.”
• Overcomplicating the Problem: Break the problem into smaller, manageable steps to avoid feeling overwhelmed.
• Forgetting Units: Pay attention to the units (such as dollars, meters, or hours) throughout the problem. This will ensure your solution is in the correct format.

With practice, solving word problems becomes easier. By systematically breaking down the information and approaching each part methodically, you can improve both your accuracy and confidence in handling these types of questions.

Tips for Solving Linear Equations

Solving linear equations involves finding the value of an unknown variable that makes the equation true. These types of problems are foundational in mathematics, and mastering them opens the door to solving more complex problems. The process can be straightforward if you follow a clear set of steps and stay organized throughout. This section will provide useful strategies to simplify and effectively solve linear equations.

Step-by-Step Approach

To solve linear equations successfully, follow this method:

1. Isolate the Variable: Begin by moving all terms involving the unknown variable to one side of the equation, and constants to the other side. This helps to simplify the equation.
2. Simplify Each Side: Combine like terms on each side of the equation before proceeding. This makes the equation easier to work with and minimizes mistakes.
3. Perform Inverse Operations: Use inverse operations (addition, subtraction, multiplication, or division) to cancel out terms around the variable. Always apply the same operation to both sides of the equation to maintain balance.
4. Check Your Solution: Once you have solved for the variable, substitute your solution back into the original equation to verify that it satisfies the equation.

Common Mistakes to Avoid

While solving linear equations is often straightforward, there are a few common errors that can lead to incorrect solutions. Here are some tips to avoid those mistakes:

• Neglecting Parentheses: Always distribute or simplify parentheses before moving terms across the equal sign. Failing to do so can cause mistakes in your calculations.
• Dividing by Zero: Be careful not to divide by zero. Always check that the denominator is not zero when performing division.
• Forgetting to Flip the Sign: When multiplying or dividing both sides of an equation by a negative number, remember to flip the inequality sign, if applicable.

By practicing these strategies and avoiding common pitfalls, you can efficiently solve linear equations and build a strong foundation for more advanced problem-solving techniques.

Checking Your Work with the Answer Key

Verifying your calculations is an essential part of the learning process. After solving mathematical problems, it’s important to compare your solutions with the correct results to ensure accuracy. This not only helps in identifying mistakes but also provides an opportunity to understand the problem-solving steps better. Here, we will explore how to effectively use reference materials to confirm your work and improve your skills.

Steps for Effective Verification

To verify your solutions and ensure that you are on the right track, follow these steps:

1. Double-Check Your Calculations: Before comparing your solutions, review each step of your work carefully. Look for simple errors such as arithmetic mistakes or misplaced signs that could lead to an incorrect answer.
2. Compare with the Correct Results: Once you’re confident in your work, check the final answers with the provided solutions. If your answer matches the correct one, you can be confident in your method. If it doesn’t, investigate where the error might have occurred.
3. Analyze the Process: It’s not just about getting the correct result. Take time to understand why the correct answer is what it is. Analyze the steps in the reference material and see if there are more efficient ways to approach the problem.
4. Learn from Mistakes: When your solutions don’t match, go back and try to pinpoint exactly where the problem arose. Learning from these errors helps build a deeper understanding of the concepts involved.

Benefits of Verifying Your Work

Using a reference to verify your answers offers several benefits that go beyond just confirming correctness:

• Improves Accuracy: Regularly checking your work helps prevent repeated mistakes and strengthens your ability to identify errors quickly.
• Boosts Confidence: When you see that your solutions match, it builds your confidence in the methods you’ve used, encouraging you to tackle more challenging problems.
• Clarifies Understanding: By comparing your methods with the reference, you can identify areas where your understanding may need improvement and take steps to address them.

By consistently verifying your solutions, you not only ensure accuracy but also foster a stronger grasp of mathematical concepts, which will benefit you in more advanced problem-solving scenarios.

Reviewing Key Terms and Definitions

In any area of study, especially mathematics, understanding the fundamental concepts and terminology is essential to mastering the subject. By familiarizing yourself with the key terms, you can approach problems with confidence and a deeper understanding. In this section, we will review some of the essential terms and definitions that form the foundation of mathematical problem-solving, helping you to build a strong base for tackling more complex topics.

Below are some key terms that are crucial for understanding basic mathematical principles:

• Variable: A symbol, often represented by a letter, that stands for a number or value that can change within the context of a problem.
• Expression: A combination of numbers, variables, and mathematical operations that represents a particular value but does not include an equal sign.
• Equation: A mathematical statement that shows the relationship between two expressions, separated by an equal sign. It asserts that the values on both sides are the same.
• Coefficient: A numerical factor that multiplies a variable in an expression or equation. For example, in 3x, 3 is the coefficient of x.
• Constant: A fixed value that does not change. In an expression or equation, a constant is typically represented by a number that is not attached to a variable.
• Solution: The value or set of values that satisfy an equation or inequality, making both sides of the equation equal.

Understanding these basic terms will provide a strong foundation for approaching more advanced mathematical concepts and solving a variety of problems effectively.

Understanding Inequalities in Algebra

In mathematics, inequalities represent relationships where one quantity is not necessarily equal to another. Unlike equations, which assert that two expressions are equal, inequalities allow for a broader range of solutions. They are used to describe situations where values are greater than, less than, or not equal to other values. In this section, we will explore the fundamental concepts of inequalities, how they differ from equations, and the techniques for solving them.

Inequalities are typically expressed using the following symbols:

• > : Greater than
• < : Less than
• ≥ : Greater than or equal to
• ≤ : Less than or equal to
• ≠ : Not equal to

When solving inequalities, it’s important to remember that the solution set can be a range of values, not just one single number. This means that the solution is often expressed in interval notation or graphically on a number line. For example, the inequality x > 3 means that any number greater than 3 is a solution.

Some key points to keep in mind when working with inequalities:

• Flipping the inequality sign: When multiplying or dividing both sides of an inequality by a negative number, the direction of the inequality symbol must be reversed.
• Compound inequalities: These involve two inequalities combined into one, such as a < x ≤ b, which means that x is between a and b.
• Graphing inequalities: When graphing an inequality on a number line, use an open circle for “greater than” or “less than” (>, <), and a closed circle for “greater than or equal to” or “less than or equal to” (≥, ≤).

Mastering inequalities is crucial, as they are used in a wide range of mathematical topics, from linear functions to optimization problems. By understanding the rules and strategies for solving them, you can confidently approach more complex problems involving inequalities.

Practice Problems and Solutions

Practicing mathematical concepts is essential for solidifying understanding and developing problem-solving skills. This section provides a series of problems designed to reinforce key principles from the first section of mathematics instruction. The goal is to apply what has been learned to solve problems step-by-step, helping to build confidence and mastery. Below are several practice exercises along with detailed solutions to guide you through the process.

Problem 1: Solving Linear Equations

Consider the equation 2x + 5 = 15. Solve for x.

Solution:

• Start by isolating the variable x. Subtract 5 from both sides: 2x = 10.
• Next, divide both sides by 2: x = 5.
• The solution is x = 5.

Problem 2: Solving an Inequality

Solve the inequality 3x – 4 > 8.

Solution:

• First, add 4 to both sides: 3x > 12.
• Next, divide both sides by 3: x > 4.
• The solution is x > 4.

Problem 3: Working with Expressions

Simplify the expression: 5(2x + 3) – 4x.

Solution:

• Distribute the 5 to both terms inside the parentheses: 10x + 15 – 4x.
• Combine like terms: (10x – 4x) + 15 which simplifies to 6x + 15.
• The simplified expression is 6x + 15.

These practice problems cover fundamental concepts, such as solving equations, working with inequalities, and simplifying expressions. By consistently practicing these types of problems, you can enhance your understanding and improve your ability to handle more complex mathematical challenges.

Improving Your Problem-Solving Skills

Enhancing your ability to solve mathematical challenges involves developing a clear, methodical approach to break down complex problems into manageable steps. By honing techniques that involve critical thinking, pattern recognition, and strategic planning, you can improve your overall problem-solving ability. This will not only help you tackle tasks with greater efficiency but also build a deeper understanding of the concepts you are working with.

Here are some effective strategies that will help sharpen your problem-solving skills:

Key Approaches to Strengthen Problem-Solving

Strategy	Description
Understand the Problem	Carefully read through the problem to ensure you fully understand what is being asked. Identify key information and determine the goal.
Break It Down	Divide the problem into smaller, easier-to-handle steps. This will prevent you from feeling overwhelmed and allow you to approach each part systematically.
Use Visual Aids	Diagrams, charts, or tables can help visualize complex problems, making it easier to spot patterns or relationships between variables.
Work Backwards	If you’re unsure where to start, try working backwards from the solution. This technique can often reveal key steps or simplify the process.
Review and Reflect	After solving the problem, take time to review your solution and reflect on the steps you took. This helps reinforce your learning and improve your approach for future problems.

Applying these strategies consistently will gradually help you develop a more structured and confident approach to problem-solving, leading to better results and a deeper understanding of the material.

How the Answer Key Supports Learning

Having access to a set of solutions can significantly enhance the learning process by providing a reference point for understanding how to approach various problems. Rather than simply checking if an answer is correct, this resource offers an opportunity to review the methods and strategies used to arrive at a solution. By analyzing the steps involved, students can gain a deeper understanding of the concepts and improve their problem-solving skills.

Here are some ways this resource contributes to the learning journey:

• Clarifies Thought Processes: Reviewing the steps in a solution helps identify where a student may have gone wrong and offers a clearer understanding of the correct approach.
• Reinforces Conceptual Understanding: By seeing the detailed steps, learners are able to reinforce their grasp of the underlying principles and how they apply to similar problems.
• Encourages Self-Assessment: Students can compare their approach with the provided solution, allowing them to assess their strengths and areas for improvement.
• Promotes Independent Learning: With access to this type of resource, students are empowered to study on their own, practice regularly, and become more self-sufficient in their learning.
• Supports Progress Tracking: By periodically reviewing the solutions, learners can track their progress over time, identifying patterns in their mistakes and improving their performance.

Ultimately, this reference tool serves as an essential part of the educational process, enabling students to build confidence and competence in their problem-solving abilities, while fostering a deeper understanding of the material.