
Mathematics can often seem challenging, especially when facing complex problems that require a deeper understanding of the concepts involved. For students tackling various topics, having access to the correct solutions can make a significant difference in their ability to grasp difficult material. By breaking down each problem step by step, learners can gain a better understanding of the methods and techniques that lead to successful outcomes.
Achieving mastery in mathematical subjects involves not only practicing problems but also understanding the logic behind each solution. With the right guidance and resources, even the most difficult exercises can be simplified. This section provides an organized approach to reviewing key concepts, offering clarity on how to work through challenging questions and find reliable solutions.
In this article, we will focus on specific examples, breaking down complex equations and offering detailed explanations for each stage. Whether you are preparing for an exam or simply looking to improve your problem-solving skills, this guide will serve as a valuable resource to reinforce your learning and ensure you are on the right track to success.
Mathematical Problem Solutions for Section 3, Exercise 4
This section provides a detailed look at the solutions for the exercises found in the third segment of the course. By reviewing these solutions, students can enhance their understanding of how to approach similar problems in the future. The breakdown of each problem demonstrates the step-by-step process needed to reach the correct conclusion.
Understanding the methods used to solve these problems is crucial for developing a strong foundation in mathematics. Each solution is carefully explained to highlight key concepts and techniques that are essential for solving more advanced questions in the field.
Step-by-Step Process for Solving Problems
- Step 1: Identify the given values and understand the problem’s requirements.
- Step 2: Apply appropriate mathematical rules and properties to simplify expressions.
- Step 3: Solve for the unknown variable by performing necessary operations.
- Step 4: Check the solution for accuracy to ensure it satisfies the initial conditions.
Key Strategies for Effective Problem Solving
- Practice: Consistent practice is the key to mastering mathematical techniques.
- Review: Always go back and check the work for any potential mistakes.
- Understand: Focus on understanding the logic behind each step rather than memorizing formulas.
- Seek Help: Don’t hesitate to reach out for guidance when a concept is unclear.
By carefully reviewing the solutions presented, students can gain a clearer understanding of the approach required for similar exercises in future sections. Mastering these fundamental techniques will prepare learners for more challenging topics and foster a deeper confidence in their mathematical abilities.
Overview of Mathematics 1
This section introduces the foundational principles of mathematics, focusing on essential concepts and techniques that students need to master. The material is designed to help learners build a strong mathematical base, which is crucial for success in more advanced studies. By understanding the core ideas presented here, students will gain the confidence to approach increasingly complex problems.
In this course, learners will engage with a variety of mathematical topics, each building upon the previous one. The goal is to develop critical thinking skills and an understanding of how mathematical concepts apply to real-world situations.
Key Topics Covered

- Basic Operations: Understanding fundamental operations such as addition, subtraction, multiplication, and division.
- Equation Solving: Learning to solve simple and complex equations using different methods.
- Graphing: Introducing the concept of graphing linear equations and interpreting graphs.
- Patterns and Relationships: Recognizing patterns and understanding how variables relate to one another.
- Problem-Solving Strategies: Developing strategies for approaching a variety of problem types efficiently.
Objectives and Benefits
- Build Mathematical Fluency: Master the essential skills necessary for higher-level mathematics.
- Develop Critical Thinking: Learn to analyze and solve problems with logical reasoning.
- Prepare for Future Courses: Equip yourself with the knowledge required for more advanced topics in mathematics.
- Apply Math to Real-Life Situations: Understand how mathematical principles can be used in practical applications.
This section aims to provide a comprehensive understanding of the key concepts, ensuring that students are well-prepared for the challenges ahead in their mathematical journey.
Understanding Section 3 Key Concepts
In this section, we will explore the fundamental principles that serve as the foundation for solving problems in this chapter. These concepts are essential for building a deeper understanding of the material, and they provide the necessary tools for tackling both simple and complex problems. Mastering these ideas will help you develop a strong problem-solving approach that can be applied to a wide range of mathematical topics.
By examining the core ideas in detail, students will better comprehend how different mathematical elements interact and how to apply these relationships effectively. This knowledge is crucial for successfully navigating more advanced material in the future.
Core Mathematical Techniques
- Solving Equations: Learning how to isolate variables and solve for unknowns.
- Understanding Functions: Exploring the relationship between input and output values in a mathematical context.
- Graphing Equations: Plotting equations on a graph and interpreting the results visually.
- Factoring: Breaking down complex expressions into simpler components to make them easier to solve.
Applying Concepts to Real-World Problems
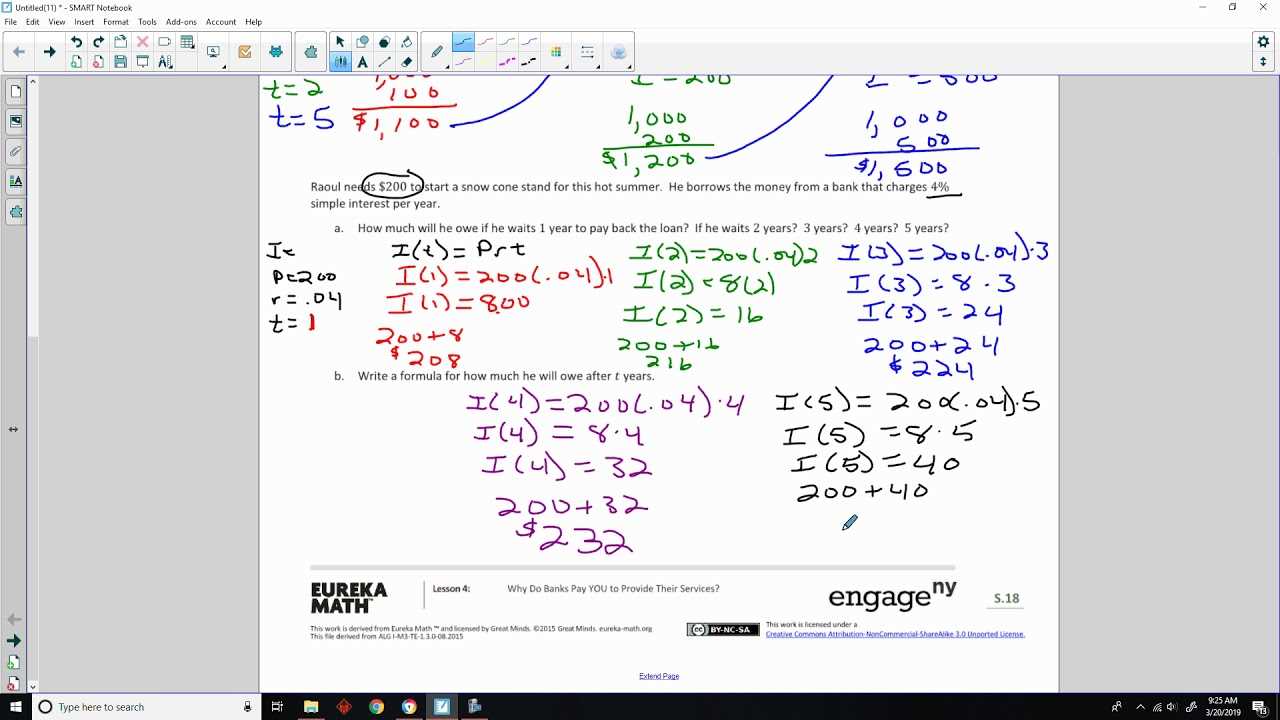
- Word Problems: Translating real-life situations into mathematical expressions and equations.
- Problem-Solving Strategies: Developing strategies to approach and solve problems efficiently and accurately.
- Modeling with Equations: Using mathematical equations to represent and solve practical situations.
By thoroughly understanding the key concepts of this section, students will be equipped with the tools necessary to approach more challenging topics with confidence and clarity.
How to Approach Section 4 Problems
When faced with mathematical problems in this section, it’s important to have a structured approach to ensure that each problem is solved efficiently. The key to success lies in breaking down each problem into manageable steps, carefully analyzing the given information, and applying the appropriate methods to find a solution. By following a clear process, you can approach even the most challenging problems with confidence.
Developing a systematic strategy for solving problems allows you to stay organized and reduces the likelihood of making mistakes. Understanding how to identify what is being asked and knowing which techniques to use are critical skills that will serve you throughout the entire course.
Step-by-Step Strategy
- Step 1: Read the problem carefully and identify the key components, such as known values and what is being asked.
- Step 2: Choose the appropriate method or formula that will help simplify the problem.
- Step 3: Perform the necessary calculations or manipulations to solve for the unknowns.
- Step 4: Review your work to ensure accuracy and verify that the solution satisfies the conditions of the problem.
Tips for Success
- Stay Organized: Write down all steps clearly to avoid confusion.
- Check Your Work: After solving, recheck each step to ensure no errors were made.
- Practice Regularly: Consistent practice helps reinforce problem-solving techniques.
By following this structured approach, you will be able to tackle the problems in this section more effectively, gaining a deeper understanding of the underlying mathematical concepts.
Step-by-Step Guide for Section 4
This guide breaks down the problem-solving process for the exercises in this section. By following these steps, students will learn how to tackle each problem in a structured and efficient manner. Each step is designed to help clarify the approach, making it easier to solve even the most complex questions.
Understanding the sequence of actions to take will ensure that you can consistently apply the right techniques, check your work, and arrive at the correct solution every time. This methodical approach is key to mastering the material and building a solid foundation for future topics.
Step-by-Step Process
| Step | Description |
|---|---|
| Step 1 | Read the problem carefully, noting the given values and what you are required to find. |
| Step 2 | Identify the appropriate method or formula needed to solve the problem. |
| Step 3 | Simplify the equation or expression by applying the necessary mathematical operations. |
| Step 4 | Perform calculations and isolate the variable to find the solution. |
| Step 5 | Review the solution to ensure that it meets the original conditions of the problem. |
By following these steps, you can approach each exercise with confidence, knowing you have a clear path to solving the problems effectively. This guide will help reinforce your understanding of the concepts and improve your overall problem-solving skills.
Frequent Errors in Mathematics 1
When solving mathematical problems, especially those involving equations and expressions, students often encounter challenges that can lead to mistakes. Recognizing and understanding these errors is crucial to improving problem-solving skills. By being aware of the most common pitfalls, learners can avoid them and strengthen their mathematical understanding.
Errors can arise from a variety of sources, such as misinterpreting the problem, skipping important steps, or applying incorrect methods. Being mindful of these issues helps students take a more methodical approach and achieve more accurate results in their work.
Typical Mistakes to Avoid
- Misunderstanding Problem Requirements: Failing to identify what the question is asking can lead to solving for the wrong variable or using the wrong method.
- Incorrect Order of Operations: Forgetting to follow the proper order (PEMDAS/BODMAS) can result in incorrect answers.
- Algebraic Sign Errors: Making mistakes with positive and negative signs, especially when simplifying or solving equations, is a frequent problem.
- Overlooking Like Terms: Not combining similar terms when simplifying expressions can lead to incorrect solutions.
- Inaccurate Distribution: Failing to correctly distribute terms when working with parentheses can cause errors in the final result.
Tips for Avoiding Mistakes
- Read the Problem Carefully: Always take the time to fully understand what is being asked before beginning to solve the problem.
- Double-Check Calculations: Review each step to ensure there are no errors in arithmetic or algebraic manipulations.
- Use Parentheses Wisely: When in doubt, use parentheses to clarify order of operations and avoid mistakes.
- Practice Regularly: Consistent practice will help you recognize patterns and become more familiar with the techniques used to solve problems.
By being aware of these common errors and taking steps to avoid them, students can enhance their accuracy and efficiency in solving problems, leading to greater success in their studies.
Reviewing Essential Mathematical Principles
In order to effectively solve problems, it’s crucial to revisit the fundamental principles that underpin mathematical operations. These basic rules provide the foundation for more complex calculations and help ensure that solutions are accurate. By understanding these core concepts thoroughly, students are better equipped to approach any type of mathematical challenge.
This section serves as a reminder of some of the most important ideas and strategies that are regularly applied in problem-solving. Reviewing these principles not only helps reinforce key knowledge but also prepares students for more advanced topics in the future.
Key Concepts to Remember
- Order of Operations: Always perform calculations in the correct sequence. The standard rule (PEMDAS) dictates that parentheses and exponents are handled first, followed by multiplication and division, and then addition and subtraction.
- Combining Like Terms: Simplify expressions by adding or subtracting terms that have the same variable and exponent.
- Distributive Property: This property allows you to multiply a single term across a sum or difference within parentheses. For example, a(b + c) = ab + ac.
- Solving Equations: The goal is to isolate the variable by performing inverse operations on both sides of the equation.
Why These Principles Matter
- Clarity in Problem-Solving: These fundamental concepts provide a clear approach to breaking down and solving complex equations.
- Accuracy: Following these rules ensures that each step in solving a problem is done correctly, leading to more accurate results.
- Building Confidence: Mastery of these principles boosts confidence in solving a wide range of mathematical problems, from basic to advanced levels.
By continually reviewing and applying these essential concepts, students will build a solid foundation for tackling more challenging topics and mastering mathematical problem-solving.
Techniques for Solving Section 4 Exercises
Approaching mathematical exercises requires a methodical strategy to ensure accurate and efficient solutions. Each problem in this section may require a slightly different technique, but the underlying principle remains the same: break down complex problems into manageable parts. By using specific problem-solving strategies, you can simplify the process and achieve correct answers with confidence.
Familiarity with various techniques not only helps in solving problems faster but also ensures that you understand the reasoning behind each step. This deeper understanding will enhance your ability to tackle new and more challenging tasks in the future.
Effective Strategies for Success
- Identify the Given Information: Carefully read the problem to understand the known values and what is being asked. Clarifying these will guide your approach.
- Choose the Right Method: Select the appropriate mathematical method or formula for the type of problem. This could involve simplifying expressions, solving equations, or using graphing techniques.
- Isolate Variables: When solving for an unknown, focus on isolating the variable on one side of the equation to make it easier to solve.
- Apply Inverse Operations: Use inverse operations (addition/subtraction, multiplication/division) to move terms around and simplify the problem.
- Check Your Work: Always review each step to ensure accuracy and check that the final solution makes sense within the context of the problem.
Additional Tips for Mastery
- Practice Regularly: The more problems you solve, the more comfortable you will become with identifying the right techniques.
- Work in Stages: Tackle complex problems one step at a time, breaking them down into smaller, simpler tasks to avoid confusion.
- Use Visual Aids: For geometric or graphing problems, use diagrams or charts to visualize relationships and better understand the problem.
By consistently applying these techniques, you will not only improve your ability to solve exercises in this section but also enhance your overall mathematical skills. With practice and patience, these methods will become second nature, preparing you for more advanced topics ahead.
Key Takeaways from Section 3
As we conclude this section, it’s essential to review the main concepts and techniques that have been covered. Understanding these core ideas will provide a solid foundation for tackling more advanced mathematical problems in the future. Each takeaway represents a crucial piece of knowledge that will support your continued progress in problem-solving and mathematical reasoning.
By revisiting the important points and practicing regularly, you will reinforce your understanding and be better prepared to move forward in your studies. Here are the primary lessons learned in this section:
Important Concepts to Remember
- Solving Linear Equations: Mastering the process of isolating variables and using inverse operations is key to solving linear equations effectively.
- Simplifying Expressions: Understanding how to combine like terms and apply the distributive property will make working with algebraic expressions easier and more efficient.
- Graphing Techniques: Knowing how to plot points and interpret graphs helps in visualizing equations and understanding their behavior.
- System of Equations: Learning how to solve systems of equations by substitution or elimination is essential for handling more complex problems.
Final Reminders
- Focus on Process: It’s not just about the answer–understanding the steps and processes involved in solving a problem is just as important.
- Practice Makes Perfect: The more you practice, the more familiar you will become with different types of problems and the techniques used to solve them.
- Review Regularly: Regularly revisiting key concepts will reinforce your understanding and help keep these skills sharp.
| Concept | Key Point |
|---|---|
| Solving Equations | Use inverse operations to isolate variables. |
| Simplifying Expressions | Combine like terms and apply distribution. |
| Graphing | Plot points and interpret graphs of equations. |
| Systems of Equations | Solve using substitution or elimination. |
These key takeaways will serve as a helpful reference as you continue to progress in your mathematical studies. By solidifying these concepts, you will build a strong foundation for tackling more challenging problems ahead.
Breaking Down Complex Mathematical Equations
Solving intricate equations requires a structured approach to simplify and solve step by step. Breaking down complex expressions involves identifying and isolating key components to make the problem more manageable. By carefully analyzing each term and applying systematic rules, you can transform even the most challenging equations into solvable parts.
Approaching these problems logically and methodically will lead to more accurate and faster solutions. In this section, we will discuss effective strategies to handle difficult equations, ensuring you understand the reasoning behind every step.
Steps for Simplifying Complex Equations
- Identify Like Terms: Look for terms that can be combined, such as constants and variables that have the same exponent.
- Distribute and Combine: Apply the distributive property where necessary to simplify expressions and group terms together.
- Isolate Variables: Move terms involving the variable to one side of the equation and constants to the other side.
- Apply Inverse Operations: Use inverse operations to eliminate coefficients and solve for the unknown.
Example of Breaking Down an Equation
Let’s look at an example to illustrate the process:
| Step | Action | Equation |
|---|---|---|
| 1 | Distribute and combine like terms | 3(x + 2) = 12 |
| 2 | Simplify the equation | 3x + 6 = 12 |
| 3 | Move constants to one side | 3x = 12 – 6 |
| 4 | Isolate the variable | x = (12 – 6) / 3 |
| 5 | Simplify the result | x = 2 |
As seen in the example, breaking the equation into smaller steps makes it easier to manage. By distributing terms, simplifying the equation, and isolating the variable, you can solve even the most complex problems with confidence.
Exploring Mathematical Word Problems
Word problems in mathematics require the translation of real-world situations into equations that can be solved. These problems often involve multiple steps and the application of various mathematical concepts to arrive at the correct solution. By breaking down the problem, identifying key information, and setting up the right expressions, even complex scenarios can be tackled with ease.
In this section, we will explore strategies for solving word problems effectively. By following a structured approach, you can understand the problem better and develop a clear path to the solution.
Key Steps for Solving Word Problems
- Read Carefully: Understand the problem completely by reading it multiple times to identify the important details.
- Identify Variables: Assign variables to the unknowns in the problem. These are the quantities you’re trying to solve for.
- Translate Words to Equations: Convert the problem’s description into a mathematical equation using appropriate operations.
- Solve the Equation: Apply the necessary mathematical techniques to solve the equation for the unknown variable.
- Interpret the Solution: Once solved, make sure the solution makes sense within the context of the problem.
Example Problem

Let’s take an example of a word problem:
A store sells notebooks for $3 each and pens for $2 each. If a student buys 5 notebooks and 4 pens, how much did they spend in total?
To solve this, we follow these steps:
- Let the number of notebooks be represented by n and the number of pens by p.
- The total cost can be expressed as 3n + 2p.
- Substitute the given values: 3(5) + 2(4).
- Simplify the equation: 15 + 8 = 23.
- The student spent a total of $23.
By carefully reading and translating the given information into a mathematical equation, the problem can be solved step by step. Understanding how to approach word problems in this manner ensures greater accuracy and clarity in finding the solution.
Strategies for Effective Problem Solving
Solving mathematical problems requires a structured approach to ensure accuracy and efficiency. Whether the task involves equations, word problems, or complex expressions, applying a consistent method can help break down the problem into manageable steps. By using proven strategies, you can improve your problem-solving skills and tackle even the most challenging tasks with confidence.
In this section, we will discuss several strategies to help streamline your approach to solving problems. These methods focus on organizing your thoughts, minimizing errors, and ensuring clarity throughout the process.
Understand the Problem
The first step in solving any problem is fully understanding it. Read the problem carefully and identify the key information. Ask yourself what is being asked and what data is provided. In many cases, restating the problem in your own words can help clarify your understanding.
Break Down the Problem
Once you understand the problem, break it down into smaller, simpler parts. If it’s an equation, isolate variables or simplify expressions. For word problems, highlight the important values and translate them into mathematical expressions. Working in stages can prevent feeling overwhelmed and helps you stay organized.
- Identify Known and Unknown Values: Clarify what information you already have and what you need to find.
- Set Up an Equation: Translate the problem into an equation or expression that you can work with.
- Solve Step-by-Step: Perform the necessary operations in order. Be methodical to avoid mistakes.
- Check Your Work: Once you find a solution, review each step to ensure you haven’t missed anything or made an error.
Applying these strategies not only makes the problem easier to solve but also improves your ability to approach new challenges. With practice, these techniques will become second nature, leading to better results in less time.
Tools to Help with Algebraic Solutions
When tackling mathematical problems, having the right tools at your disposal can significantly improve the process and outcome. From basic calculators to specialized software, various resources can aid in simplifying complex tasks, reducing errors, and enhancing your understanding of mathematical concepts. These tools are designed to assist you in breaking down problems, checking your work, and visualizing solutions effectively.
In this section, we will explore a few useful tools and techniques that can support you in finding solutions more efficiently. By integrating these tools into your problem-solving routine, you can work with greater precision and confidence.
Graphing Calculators
Graphing calculators are invaluable for solving equations and visualizing mathematical relationships. They allow you to plot functions, find intersections, and analyze patterns, all of which can simplify the process of solving complex equations. With advanced functions such as solving systems of equations or graphing inequalities, these calculators provide a comprehensive approach to problem solving.
Online Calculators and Solvers

There are many online tools available that can solve equations and offer step-by-step explanations. Websites such as WolframAlpha, Symbolab, and Desmos provide easy access to powerful solvers. These tools can help verify your solutions, offer different methods of solving, and sometimes provide interactive graphs to deepen your understanding.
- WolframAlpha: A computational engine that solves a wide range of problems, from basic arithmetic to complex equations.
- Symbolab: An online solver that provides detailed solutions and explanations, making it easier to understand each step.
- Desmos: A graphing calculator tool that visualizes functions, making it ideal for exploring equations in graphical form.
These tools not only streamline the process of finding solutions but also foster a deeper understanding of mathematical concepts by offering multiple perspectives on how to approach a problem.
Tips for Mastering Algebra 1 Units
Mastering mathematical concepts requires a mix of strategy, practice, and the right approach to learning. Whether you’re tackling basic operations or more complex equations, focusing on a few key techniques can make a significant difference. The following tips will guide you through the process of becoming proficient in these subjects, helping you gain a deeper understanding and confidence in your problem-solving abilities.
To succeed in any mathematics course, it’s important to stay organized, seek clarification when needed, and focus on consistently practicing the material. Below are some valuable tips to help you strengthen your skills and improve your performance.
Stay Organized and Set Goals
Effective organization is key to mastering new material. Break down topics into smaller sections, focus on one concept at a time, and keep track of your progress. Establish specific goals for each study session to stay on track and measure your improvement.
Practice Regularly
The more you practice, the more familiar and comfortable you will become with different types of problems. Regular practice not only reinforces the material but also builds the problem-solving habits you need to excel.
Understand the Fundamentals

Before moving on to more advanced concepts, make sure you have a solid understanding of the fundamentals. A strong foundation will help you grasp more complex ideas quickly and prevent confusion later on. If you’re struggling with a specific concept, take the time to revisit it until it becomes clear.
Use Visual Aids
Visual tools, such as graphs and charts, can be extremely helpful when trying to understand mathematical relationships. Use them to see the patterns, identify key points, and better understand the connections between different concepts.
Collaborate with Peers
Working with others can provide fresh perspectives on solving problems. Don’t hesitate to ask for help when needed, and try explaining your solutions to others. Teaching the material can deepen your own understanding.
| Tip | Description |
|---|---|
| Stay Organized | Keep track of your progress and break down complex topics into manageable sections. |
| Practice Regularly | Consistency is key. Practice problems frequently to build strong skills. |
| Understand the Basics | A strong understanding of foundational concepts is essential for mastering advanced topics. |
| Use Visual Aids | Graphs and diagrams can help you visualize concepts and relationships more clearly. |
| Collaborate | Work with others to gain different insights and clarify challenging topics. |
By following these strategies and dedicating time to each area, you can greatly enhance your ability to understand and solve problems. With patience and persistence, you’ll be well on your way to mastering the material and achieving success in your studies.
How the Answer Key Supports Learning
Providing solutions for mathematical exercises is an essential tool for reinforcing understanding and improving problem-solving skills. By reviewing the completed solutions, students can identify where they made mistakes, how they can correct them, and what strategies they might apply in future problems. This practice helps solidify concepts and enhances overall comprehension.
An effective set of solutions serves not only as a reference point but also as a learning aid. It allows learners to compare their thought process with a correct approach, fostering a deeper understanding of the steps involved in each problem. By using these solutions, students can pinpoint patterns and identify key techniques that can be applied to similar problems.
Furthermore, having access to detailed solutions can boost confidence. It offers learners the reassurance that they are on the right track, especially after encountering challenges. This process of self-assessment can motivate students to continue working through more problems and apply the strategies they have learned. In turn, it supports independent learning and builds critical thinking skills.
Ultimately, solutions are more than just the correct answers; they act as a guide, helping students analyze their mistakes, refine their problem-solving approach, and gain a clearer understanding of mathematical concepts. The availability of these resources encourages students to approach learning with a proactive mindset, promoting both mastery and confidence.
Study Resources for Mastering Mathematical Concepts
When tackling mathematical topics, having the right resources at hand can make all the difference. These resources help reinforce learned material, clarify complex concepts, and provide valuable practice opportunities. Whether you’re looking to enhance your understanding of core principles or solve more challenging problems, various tools and study aids can support your learning journey.
Online Learning Platforms
Many websites and educational platforms offer interactive tools and lessons designed to enhance learning. These resources provide video tutorials, quizzes, and practice exercises that cover a wide range of topics.
- Khan Academy – Offers comprehensive lessons with practice exercises for a variety of mathematical topics.
- IXL – Provides personalized learning plans and skill-building exercises.
- Mathway – An online tool for solving problems and showing step-by-step solutions.
Textbooks and Workbooks
Traditional textbooks and workbooks are still invaluable for reviewing key concepts. These resources provide structured lessons and practice problems that guide students through various levels of difficulty.
- “Pre-Algebra” by McDougal Littell – A solid choice for students looking for step-by-step guidance and explanations.
- “Understanding Mathematics” by Cengage Learning – Offers an in-depth approach to mastering mathematical techniques.
- Practice workbooks – These books often provide hundreds of problems to hone skills and prepare for tests.
Using a combination of these resources will help reinforce concepts, build problem-solving strategies, and improve overall mathematical understanding. Whether you prefer self-paced learning through online platforms or structured guidance through textbooks, the key to success is consistent practice and utilizing the right materials.
Improving Your Mathematical Skills
Mastering mathematics requires consistent practice, a strong foundation in key concepts, and the ability to approach problems from different angles. To strengthen your skills and build confidence, it’s important to apply various techniques and methods that cater to your individual learning style. Whether you’re tackling simple equations or complex word problems, the path to improvement is built on understanding, practice, and feedback.
Start with the Basics: Begin by ensuring you have a solid understanding of fundamental principles. Even complex problems often rely on basic skills such as arithmetic operations, understanding variables, and working with expressions. Revisit foundational topics if needed, as these serve as building blocks for more advanced problems.
Practice Regularly: Just like learning a musical instrument, consistent practice is key to improvement. Solve a variety of problems, focusing on different techniques and strategies. The more you practice, the more familiar you become with patterns and methods used to solve problems efficiently.
Break Down Complex Problems: When facing challenging tasks, it’s essential to break them down into smaller, manageable steps. Identify what is being asked, simplify the equation, and approach each part logically. This step-by-step method helps you stay organized and reduces the chances of making mistakes.
Seek Feedback: Whether from peers, teachers, or online forums, feedback plays a crucial role in improving your skills. Understanding where you may have gone wrong helps you avoid repeating mistakes in the future. Additionally, learning from different perspectives can introduce new problem-solving strategies.
Use Resources Effectively: Leverage study guides, online tutorials, and educational platforms to gain a deeper understanding of complex topics. These tools often provide explanations, examples, and practice exercises that can clarify confusing concepts and offer extra practice opportunities.
By focusing on these strategies, you’ll gradually build your mathematical proficiency and gain confidence in solving increasingly challenging problems. Keep challenging yourself, and remember that improvement comes with time and effort.