In any learning journey, mastering mathematical concepts can be both challenging and rewarding. This section is designed to support students and educators in tackling complex problems with confidence. By providing detailed solutions and explanations, we aim to enhance understanding and encourage independent thinking in the subject.
Whether you’re revising specific problems or attempting new exercises, having a resource to verify your solutions is invaluable. This guide offers a structured approach to solving various tasks, helping to clarify difficult areas and reinforce key principles. With a clear breakdown of each step, you can ensure a deeper grasp of the material and strengthen your problem-solving skills.
Utilizing a comprehensive reference like this is essential for progressing through more advanced topics. The examples provided not only offer solutions but also demonstrate the thought processes behind them, making it easier to replicate success in future challenges. Mastering these concepts will provide a solid foundation for further learning and application in real-world situations.
Mathematical Problem Solving Guide
This section offers a comprehensive approach to verifying and understanding solutions for various mathematical exercises. It is designed to assist learners by providing clear, step-by-step explanations for each problem, ensuring that key concepts are not only learned but also applied effectively. By breaking down each task into manageable parts, students can identify areas of difficulty and strengthen their overall skills.
In order to fully grasp the material, it’s crucial to understand the reasoning behind the solutions, not just the final result. This guide helps learners visualize the problem-solving process, allowing them to replicate these strategies on similar challenges. Below is a sample table that outlines some of the most common types of problems, along with their respective solutions.
| Problem Type | Steps to Solve | Solution |
|---|---|---|
| Angle Calculation | Identify angles, apply theorems, simplify equations | 45° |
| Area of Shape | Use formulas, substitute values, solve for area | 64 sq. units |
| Volume of Solid | Find dimensions, apply volume formula | 150 cubic units |
By using this format, students can better understand how to approach each type of task. The more they practice with such structured guidance, the more confident they will become in solving complex problems independently.
How to Use the Solution Guide
Knowing how to effectively utilize a solution guide is crucial for enhancing learning. This resource is not just about checking if your answers are correct, but also about understanding the reasoning behind each solution. By carefully reviewing the steps, you can gain valuable insights into the problem-solving process and improve your approach for future tasks.
Start by attempting the problems on your own before referencing the guide. This ensures that you actively engage with the material and test your understanding. Once you’ve worked through a problem, compare your approach and result with the detailed steps provided. Pay close attention to the logic and methods used, as this will help you refine your problem-solving techniques.
Additionally, make use of the explanations to identify where mistakes may have occurred. If your answer doesn’t match, focus on the steps you took and look for any miscalculations or misunderstandings. Using this guide as a learning tool rather than just a way to confirm answers will allow you to strengthen your skills and build confidence in tackling similar problems on your own.
Understanding Essential Mathematical Concepts
Grasping the fundamental principles of mathematics is essential for building a strong foundation in solving problems. These key ideas serve as the building blocks for tackling more complex challenges. A clear understanding of these core concepts helps to recognize patterns, apply formulas accurately, and think critically about different situations.
At the heart of mathematical problem solving lies the ability to visualize relationships between shapes, sizes, and quantities. This includes understanding how to measure dimensions, calculate areas, and work with various types of figures. By focusing on the underlying principles behind each calculation, you not only arrive at the correct results but also gain a deeper insight into the nature of mathematical reasoning.
As you progress, it’s important to make connections between these concepts. For example, recognizing how the properties of angles relate to the sides of a shape or how volume relates to surface area is crucial for solving more advanced tasks. Focusing on these foundational ideas allows you to approach more challenging problems with greater confidence and precision.
Tips for Solving Mathematical Problems
Successfully solving math problems requires a methodical approach and a deep understanding of the underlying concepts. It’s important to develop strategies that help you work through each challenge step by step, ensuring that you’re not just finding the answer, but also learning the process behind it. Here are some practical tips to guide you through problem-solving tasks.
Break Down the Problem
Start by carefully reading the problem and identifying the given information and what you’re asked to find. Breaking the task into smaller, manageable parts makes it easier to focus on each step and avoids feeling overwhelmed. Look for key details that will help you set up equations or apply specific formulas.
Visualize the Problem
Whenever possible, sketch a diagram or chart to visualize the relationships between the elements in the problem. Drawing a diagram not only makes abstract concepts more tangible but also helps in identifying patterns or connections that might not be immediately obvious. This can be especially helpful when working with shapes and dimensions.
| Strategy | Description | Example |
|---|---|---|
| Use Formulas | Apply the correct formulas based on the problem type | Use the area formula for rectangles: length x width |
| Check Units | Ensure that all measurements are in the correct units | Convert from meters to centimeters if necessary |
| Double-Check Work | Review each step to ensure no mistakes were made | Recalculate values to verify results |
By applying these strategies, you’ll improve your ability to tackle problems effectively and gain confidence in solving even the most challenging tasks. Remember, practice is key to mastering mathematical concepts, and using these tips will help you develop a more structured and thoughtful approach to each problem.
Key Topics Covered in the Curriculum
This section highlights the essential concepts and areas of focus that form the foundation of this mathematical curriculum. The goal is to ensure that students not only learn the fundamental theories but also understand how to apply them in various situations. Below are some of the major topics covered that contribute to building a strong mathematical skillset.
Shapes and Their Properties
One of the core components of the study involves understanding different types of shapes and their characteristics. Students explore various geometric figures and learn how to calculate their measurements, such as area, perimeter, and volume.
- Circles: Understanding radius, diameter, and circumference
- Triangles: Properties of different types, including equilateral, isosceles, and scalene
- Quadrilaterals: Focus on rectangles, squares, parallelograms, and trapezoids
- Polygons: Exploring regular and irregular polygons
Relationships Between Angles
Angles are another key topic, as they appear in nearly every type of geometric figure. Students learn how to measure, compare, and apply angle relationships in various contexts, which is essential for solving many types of problems.
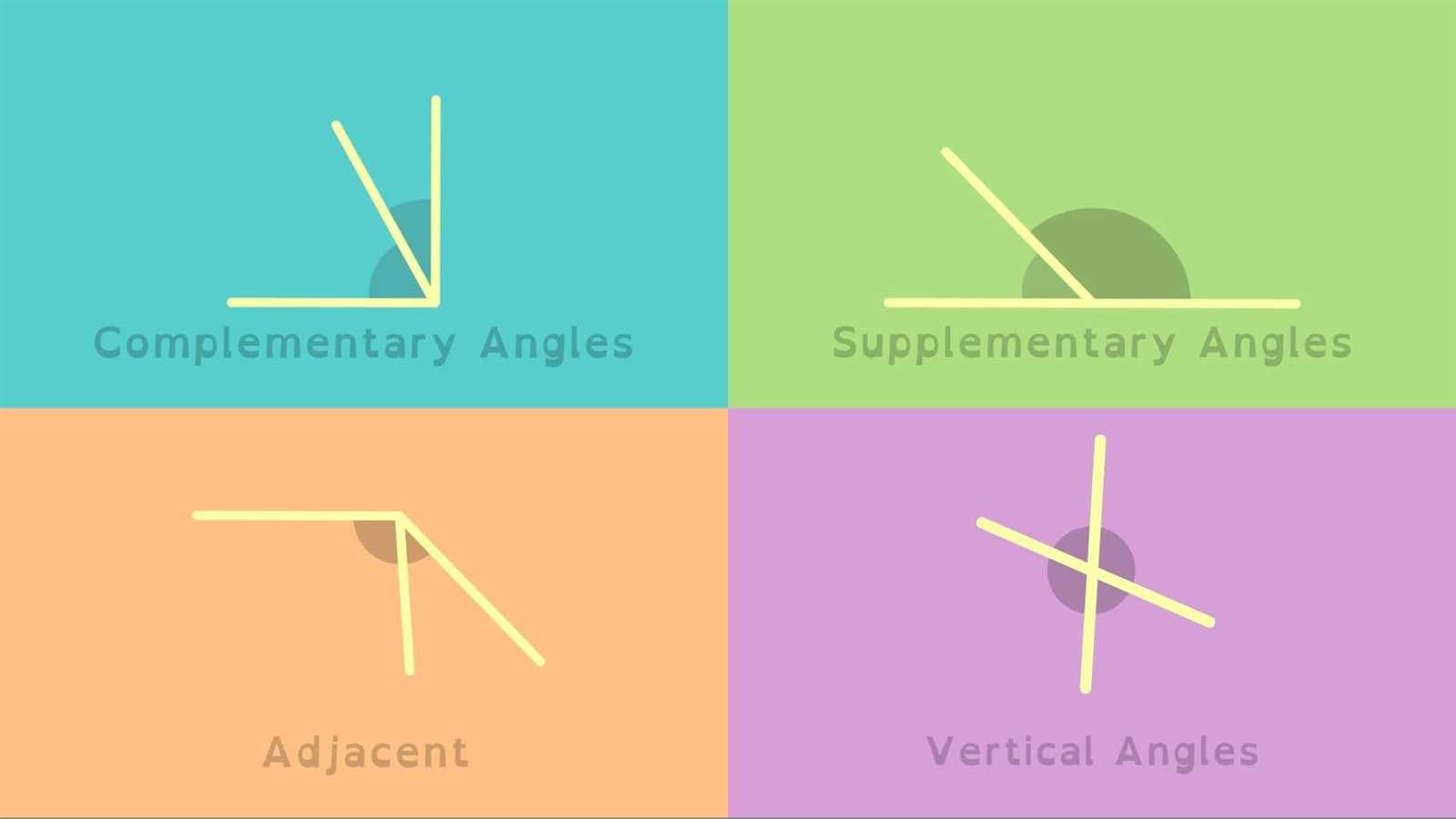
- Complementary and Supplementary Angles: How two angles relate to one another
- Vertical Angles: Understanding their properties and calculations
- Angle Sum Theorems: The sum of angles in polygons and triangles
These topics serve as the building blocks for more advanced studies, providing students with the tools to analyze, measure, and solve real-world problems involving shapes and spatial relationships. Mastery of these concepts is essential for progressing to more complex mathematical challenges.
Step-by-Step Problem Solving Guide
Approaching mathematical problems with a clear and structured method is essential for effective learning. Breaking down each problem into manageable steps allows you to focus on individual components and ensures that you can solve even the most complex tasks. Below is a guide to help you tackle problems in a logical and organized manner.
- Read the Problem Carefully: Take time to understand what is being asked. Identify the given information and the unknowns that need to be solved.
- Organize the Information: Write down all relevant data, such as measurements or relationships between elements. This helps to visualize the problem.
- Choose the Right Approach: Determine which mathematical concepts or formulas are most suitable for solving the problem.
- Work Through the Steps: Apply the chosen method step by step. Break down complex equations or figures into smaller, easier-to-manage parts.
- Check for Accuracy: After solving, review each step to ensure no mistakes were made in calculations or reasoning.
- Verify the Final Answer: Make sure the result aligns with the conditions of the problem. If possible, double-check your solution with an alternative method.
By following these steps, you’ll not only be able to find solutions more effectively but also build a deeper understanding of the processes involved. This structured approach encourages problem-solving confidence and enhances your ability to handle increasingly difficult tasks.
Common Challenges in Mathematical Problem Solving

Mathematical problem-solving often presents various challenges, particularly when working with shapes, measurements, and relationships. These difficulties can arise from misunderstandings of key concepts or from the complexity of the problems themselves. Recognizing common obstacles helps learners approach problems with a clearer mindset and better strategies for success.
Understanding Complex Figures

One of the most frequent challenges is working with intricate shapes and their properties. Many problems require knowledge of different types of figures, their dimensions, and how to manipulate them within mathematical equations. Misinterpreting angles, sides, or relationships between parts of a figure can lead to errors in calculations.
- Confusion between similar and congruent shapes
- Difficulty visualizing three-dimensional objects
- Forgetting to apply key theorems for specific shapes
Applying theorems and Formulas
Another common issue is not fully understanding when and how to apply specific mathematical formulas or theorems. Whether it’s calculating the area, volume, or perimeter, applying the correct formula in the right context is crucial. Mistakes often occur when learners try to use a formula without considering the nature of the problem.
- Incorrect use of Pythagoras’ theorem
- Forgetting to adjust units in formulas
- Confusion between surface area and volume calculations
Overcoming these challenges requires practice, patience, and a solid understanding of the underlying principles. As you gain more experience with different types of problems, you’ll develop strategies to handle these common obstacles more effectively.
Importance of Practice in Mathematics
Consistent practice is essential for mastering mathematical concepts and building a strong foundation for solving complex problems. While understanding the theory is important, applying that knowledge through repeated exercises helps to reinforce learning and develop critical thinking skills. Practice not only improves accuracy but also increases confidence in tackling various challenges.
By regularly working through problems, learners become more comfortable with different types of calculations, figure manipulation, and problem-solving strategies. This hands-on approach strengthens memory retention and enables individuals to recognize patterns and connections more quickly.
Benefits of Continuous Practice
- Improved Problem-Solving Skills: The more you practice, the more efficient you become at recognizing patterns and applying the right methods.
- Better Understanding of Concepts: Repeatedly working with different problems deepens your understanding of theoretical principles and how they relate to real-world scenarios.
- Increased Speed and Accuracy: Regular practice helps reduce mistakes and allows you to complete tasks faster and more accurately.
How to Make Practice Effective
- Start with Basic Problems: Begin with simpler tasks to build your confidence before progressing to more complex challenges.
- Focus on Weak Areas: Identify topics that are difficult and spend extra time practicing those areas to strengthen your overall understanding.
- Review Mistakes: When you make errors, take the time to understand where you went wrong and how to avoid similar mistakes in the future.
Incorporating regular practice into your study routine is crucial for success in mathematics. The more you engage with the material, the more fluent and confident you will become in applying your knowledge to solve problems efficiently.
How the Solution Guide Can Improve Learning
Having access to a solution guide can significantly enhance the learning process by providing clear examples of how to approach and solve problems. By reviewing step-by-step explanations, students can understand the logic and reasoning behind each solution, which helps to reinforce their understanding of mathematical concepts. This resource offers valuable insights that support independent learning and build confidence in problem-solving.
When used effectively, a solution guide not only helps learners check their work but also serves as a powerful tool for identifying and correcting mistakes. Understanding where errors were made can lead to deeper insights into the subject and improve overall performance. Furthermore, seeing different methods for solving the same problem allows students to choose the most efficient approach for their own learning style.
Benefits of Using a Solution Guide

- Clarifies Concepts: A well-explained solution shows how to apply concepts correctly, making abstract ideas more tangible and easier to grasp.
- Promotes Independent Learning: Reviewing solutions encourages students to think critically and solve similar problems on their own without constant guidance.
- Reinforces Mistake Correction: Identifying where and why mistakes occurred helps students learn from their errors, preventing them from repeating the same mistakes.
How to Use the Solution Guide Effectively
- Work Through Problems First: Try solving problems on your own before checking the solution guide. This encourages critical thinking and problem-solving practice.
- Review Step-by-Step: When using the solution guide, carefully study each step and understand the reasoning behind it. This process helps reinforce learning.
- Analyze Mistakes: When comparing your solution to the guide, focus on areas where your answers differ. Identify any misunderstandings and use the guide to clarify them.
By leveraging a solution guide in this way, learners can improve their comprehension and increase their problem-solving abilities, ultimately becoming more confident and proficient in their mathematical skills.
Worksheets and Exercises Explained
Worksheets and exercises play a crucial role in helping students practice and reinforce the concepts learned in mathematics. These tools provide opportunities to apply theoretical knowledge to practical problems, fostering deeper understanding and greater retention. By engaging with a variety of problems, learners develop essential skills needed to approach more complex tasks.
The Purpose of Worksheets

Worksheets are designed to give students hands-on experience with different types of problems, allowing them to familiarize themselves with key concepts and methods. Each worksheet typically covers specific topics, offering a structured way to practice and improve proficiency. By working through a series of exercises, students can identify areas where they need further study and strengthen their grasp of the material.
- Helps in reinforcing learned concepts
- Provides a variety of problems for comprehensive practice
- Allows students to track progress and identify weaknesses
How Exercises Enhance Learning
Exercises are vital for honing problem-solving abilities and ensuring that concepts are well-understood. Regular practice with exercises challenges students to think critically, apply what they’ve learned, and develop their reasoning skills. As they encounter a range of scenarios, they become more confident and efficient in handling different mathematical situations.
- Strengthens logical thinking and critical reasoning
- Enhances understanding of formulas and their applications
- Encourages active engagement with the material
By consistently completing worksheets and exercises, learners gradually build their ability to tackle increasingly complex problems with ease and accuracy.
Understanding the Curriculum Structure
The curriculum structure is designed to guide students through a progressive learning journey, focusing on building a strong foundation of mathematical principles. By introducing concepts in a systematic and step-by-step manner, the program ensures that learners gain a deep understanding of essential topics before moving on to more advanced material. This approach not only supports mastery of individual concepts but also encourages the development of critical thinking and problem-solving skills.
The curriculum emphasizes both theoretical knowledge and practical application, enabling students to connect abstract ideas with real-world scenarios. It is structured to promote active learning through exercises, projects, and collaborative activities, allowing students to engage with the material in diverse ways. Each unit is carefully crafted to enhance comprehension, with a balance between explanation, practice, and assessment to track progress.
Ultimately, the goal is to equip students with the skills they need to approach complex problems with confidence, using a logical and methodical approach to find solutions. By following this well-organized curriculum, learners build a comprehensive understanding that prepares them for future academic success and practical challenges.
Common Mistakes to Avoid in Mathematics
As students delve into mathematical concepts, there are several common pitfalls that can hinder their understanding and problem-solving abilities. Recognizing and avoiding these mistakes is crucial for mastering the subject and achieving accuracy in solutions. Many errors stem from misinterpreting problems, overlooking essential details, or failing to apply the correct methods consistently. Being aware of these issues helps learners refine their skills and develop a stronger grasp of the material.
Frequent Errors in Problem Solving
When solving mathematical problems, students often make the mistake of skipping steps or rushing through calculations. This can lead to minor errors that snowball, affecting the entire solution process. Additionally, misunderstanding terminology or misapplying formulas can cause significant setbacks. It’s important to stay methodical and precise to avoid these frequent issues.
| Common Mistake | Impact | How to Avoid |
|---|---|---|
| Skipping Steps | Leads to incomplete or incorrect solutions | Break down problems into smaller, manageable parts |
| Misunderstanding Terms | Incorrect interpretation of the problem | Review definitions and understand key concepts |
| Incorrect Formula Application | Leads to wrong results | Double-check formulas and their correct usage |
Tips for Preventing Errors
To avoid these mistakes, take the time to carefully read through each problem and ensure you understand every detail before starting. Use a structured approach to solve each task, writing out every step clearly. When in doubt, check your work to verify that all steps align with the correct methods and formulas. By consistently practicing these strategies, learners can minimize errors and improve their problem-solving accuracy.
How Mathematics Builds Critical Thinking Skills
Mathematics is not just about numbers and equations; it’s a powerful tool for developing critical thinking skills. By engaging with mathematical problems, students learn to analyze situations, evaluate different strategies, and draw logical conclusions. This process helps build a mindset that is essential for solving complex problems in various areas of life, beyond just academics.
One of the core benefits of studying mathematical concepts is the ability to think logically and systematically. Every problem presents a unique challenge that requires careful consideration of facts, data, and possible outcomes. Through repeated practice, learners refine their decision-making abilities and develop the confidence to tackle difficult tasks with clarity and precision.
How Problem Solving Promotes Critical Thinking
Solving mathematical problems forces individuals to think critically and make reasoned decisions based on available information. The process encourages breaking down larger problems into smaller, manageable parts and examining them from different perspectives. This practice builds the ability to think creatively and find solutions in situations that may initially seem insurmountable.
- Develops the ability to assess complex situations
- Encourages thoughtful analysis and logical reasoning
- Teaches how to approach problems step-by-step
Practical Applications of Critical Thinking

The critical thinking skills gained through studying mathematics extend far beyond the classroom. These skills are applicable in everyday life, from making decisions in the workplace to solving personal challenges. By strengthening reasoning and problem-solving abilities, learners are equipped to make informed choices and face obstacles with a strategic approach.
- Improves decision-making in real-world scenarios
- Helps in understanding complex information and finding patterns
- Encourages independent thinking and adaptability
Importance of Visualizing Mathematical Problems
Visualizing problems is a crucial skill when it comes to solving complex challenges. By picturing a scenario or diagram in your mind, you can gain a clearer understanding of the problem and its underlying structure. This method of visualization helps students break down abstract concepts into more manageable and concrete elements. It transforms difficult questions into something more intuitive, allowing for easier analysis and solution discovery.
When tackling mathematical tasks, drawing diagrams or creating mental images can significantly enhance comprehension. These visual aids act as powerful tools, helping to connect theoretical knowledge with real-world applications. By mapping out information visually, learners can track relationships, spot patterns, and identify the necessary steps needed to reach a solution. This approach not only simplifies problem-solving but also boosts confidence in handling more complicated scenarios.
How Visual Representation Enhances Understanding
Creating a visual representation of a problem can offer multiple benefits. It allows students to see the relationships between different elements of the problem, making it easier to grasp connections and dependencies. This clarity can lead to faster solutions, as it encourages an organized approach to tackling tasks. Visualizing also improves memory retention, as associating images with concepts strengthens the mental connection to the material.
- Clarifies complex relationships between elements
- Encourages systematic thinking and step-by-step analysis
- Helps with spatial reasoning and understanding shapes
Practical Tips for Visualization
To improve your ability to visualize problems, start by sketching out diagrams, charts, or graphs whenever possible. Even simple shapes and arrows can help clarify ideas and bring abstract concepts to life. Additionally, try to mentally picture different scenarios before committing to a solution strategy. This exercise helps improve your spatial awareness and sharpens your problem-solving skills.
- Draw simple diagrams to represent data or relationships
- Use color coding to distinguish between different elements
- Practice imagining the problem in 3D for a better understanding
How to Check Your Solutions Effectively
Ensuring the accuracy of your work is a crucial step in problem-solving. It involves reviewing each step of the process to identify potential mistakes or inconsistencies. Checking your solutions not only helps confirm correctness but also enhances your understanding of the material. By approaching the verification process systematically, you can identify errors early and strengthen your problem-solving skills.
Effective checking is more than just verifying numbers. It requires a thoughtful approach that includes re-evaluating your methods and ensuring that the logical flow of steps makes sense. Whether it’s a mathematical calculation, a formula, or a written explanation, it’s essential to question each part of the solution and ask if it aligns with the problem requirements. This approach prevents overlooked mistakes and solidifies the learning process.
Steps to Verify Your Solutions
To check your work effectively, follow a few simple steps. First, review the problem statement to ensure that you fully understand the question. Second, trace through your solution step-by-step, confirming that each step follows logically from the previous one. Finally, check your final result against the original problem to see if it makes sense in the given context.
| Step | Action |
|---|---|
| Step 1 | Review the problem statement |
| Step 2 | Go through each step of your solution |
| Step 3 | Check your final result against the problem |
Common Techniques for Effective Review
There are several methods you can use to ensure that your solutions are accurate. One approach is to work backwards from your final result to the initial conditions of the problem. This reverse process often helps spot inconsistencies or mistakes. Another useful technique is comparing your answer with other methods or similar problems to check for consistency.
- Work backwards from your final result
- Compare with other problems for consistency
- Use alternative methods to solve the problem and check results
Using the Solution Guide for Self-Study
Self-study can be a highly effective way to reinforce your understanding and improve your problem-solving skills. One valuable resource in this process is the solution guide, which offers explanations and correct responses to problems. By reviewing solutions after attempting the exercises on your own, you can identify gaps in your knowledge and learn from any mistakes. This method not only helps verify your results but also provides an opportunity to see alternative approaches to solving problems.
When using a solution guide for self-study, it’s essential to approach it with a critical mindset. Don’t just look for the right answer; take time to understand the reasoning behind each step. This deeper exploration will help you internalize concepts and build a more comprehensive understanding of the material. By comparing your methods with the guide’s explanations, you can improve your technique and develop more effective strategies for solving similar problems in the future.
Incorporating this method into your study routine can significantly enhance your learning process. Instead of passively accepting the provided solutions, actively engage with the material to strengthen your grasp of key concepts and techniques.
Where to Find Additional Resources
Finding reliable resources can greatly enhance your understanding of mathematical concepts and problem-solving techniques. There are several platforms and materials available to help you deepen your knowledge and improve your skills. Whether you prefer online tools, textbooks, or interactive exercises, a variety of options can support your learning journey.
Here are some of the best places to search for supplementary materials:
- Online Educational Platforms: Websites such as Khan Academy, Coursera, and edX offer free courses and tutorials on a wide range of topics, including mathematical concepts.
- Practice Websites: Platforms like IXL and Mathway provide interactive problems and solutions that allow you to practice and refine your skills.
- YouTube Channels: Many educators and content creators share step-by-step lessons and explanations for different types of problems. Channels like PatrickJMT and 3Blue1Brown are great for visual learners.
- Textbooks and Study Guides: Some textbooks come with companion websites that include additional practice exercises and video explanations. Study guides and workbooks can also be helpful for structured practice.
- Online Forums: Participating in online communities such as Stack Exchange or Reddit allows you to ask questions, share knowledge, and learn from others’ experiences.
By utilizing these resources, you can reinforce your understanding, discover new techniques, and tackle problems with confidence.