
In this section, we explore essential mathematical principles related to three-dimensional shapes. These concepts are fundamental for anyone looking to deepen their understanding of geometric properties, especially when it comes to calculating different measurements that describe the size and exterior of objects.
By applying these principles, learners can solve practical problems that involve determining the dimensions of solids. This involves using a variety of formulas that are essential for anyone studying geometry, helping to strengthen both theoretical knowledge and practical skills.
Through a set of practice exercises and detailed solutions, you’ll gain a clearer understanding of how to approach problems, avoid common errors, and master these key concepts. This guide will walk you step-by-step, providing valuable insights and techniques to tackle a wide range of related challenges.
Course 1 Chapter 10 Answer Key Overview
This section offers a comprehensive guide to solving geometric problems related to the size and external measurements of solid figures. By reviewing detailed solutions, students can better understand the logical steps needed to arrive at the correct results. This overview highlights the importance of mastering calculation techniques and applying them to various problems encountered in geometry.
Each solution provided in this guide is designed to clarify key concepts and demonstrate practical methods for solving complex problems. The emphasis is on reinforcing problem-solving skills, ensuring that learners can confidently navigate through similar challenges in the future. In addition, the exercises are structured to help students identify common pitfalls and enhance their overall comprehension of the material.
By carefully studying the solutions presented here, learners will develop a strong foundation in understanding geometric measurements, which will serve as a valuable asset for more advanced topics in mathematics. This guide is an essential resource for anyone looking to strengthen their grasp on the subject and achieve greater success in geometric problem-solving.
Understanding Volume and Surface Area Concepts
In this section, we dive into fundamental ideas related to the measurement of solid objects. These concepts focus on how to calculate the interior capacity and outer dimensions of three-dimensional shapes. Mastering these principles is essential for solving problems that involve real-world applications like designing containers or determining material usage.
To grasp these ideas, it’s important to recognize the distinct roles of interior space and external boundaries. Each measurement requires specific techniques and formulas to find, and understanding their relationship helps in solving practical geometry problems effectively. Developing a solid foundation in these concepts will allow you to confidently approach a variety of tasks, both academic and everyday challenges.
Key Formulas for Volume and Surface Area
This section outlines the essential formulas used to determine the size and outer dimensions of three-dimensional figures. These mathematical expressions are crucial for solving a wide range of problems related to geometric shapes. Knowing the correct formula to apply in different situations helps streamline calculations and ensures accuracy in determining the necessary measurements.
Each formula is designed to cater to specific types of solids, from rectangular prisms to spheres. Understanding when and how to use these formulas is key to solving geometric challenges effectively. Mastering these equations will empower you to tackle more complex scenarios, providing a strong foundation for future mathematical studies.
How to Calculate Volume of Prisms
To determine the capacity of a prism, it’s important to understand its basic structure and the formula used to calculate the amount of space it occupies. A prism is characterized by two parallel, congruent bases, and the height is the perpendicular distance between them. The method for calculating the space inside the prism involves multiplying the area of the base by the height.
Step-by-Step Process
Start by finding the area of the base, which will vary depending on the shape of the base (square, triangle, etc.). Once you have the area, multiply it by the height of the prism. The result gives you the total amount of space contained within the shape.
Example Problem
For a rectangular prism, calculate the area of the base by multiplying the length and width, then multiply this result by the height to find the total space inside. This approach applies to all types of prisms, with the base shape determining how you calculate the area.
Surface Area of Cylinders Explained
The outer dimensions of a cylinder can be found by calculating the total length of its sides and its circular ends. The process involves adding up the areas of these two components to get the full exterior measurement. Understanding how to find the total surface is crucial for problems where you need to determine how much material is needed to cover a cylindrical object, like a can or pipe.
Formula for Surface Calculation
To calculate the total external measurement of a cylinder, you need to account for both the curved surface and the two circular bases. The formula is given by:
2πr² + 2πrh,
where r is the radius of the circular base and h is the height of the cylinder. The term 2πr² calculates the area of the two bases, while 2πrh represents the curved surface wrapped around the sides.
Example Problem
If you have a cylinder with a radius of 4 units and a height of 10 units, substitute these values into the formula:
2π(4)² + 2π(4)(10).
This will give you the total external measurement for the cylinder, allowing you to easily determine how much material is required to cover it.
Steps to Find the Volume of Cones
Calculating the interior capacity of a cone involves using a formula that considers both the size of its circular base and its height. Since a cone tapers to a point, its capacity is a fraction of a cylinder’s, which is why the formula includes a factor of one-third. Understanding the process helps in applying the correct formula and achieving accurate results in real-life scenarios.
Formula for Interior Capacity
The formula to calculate the capacity of a cone is:
1/3 × πr²h
where r is the radius of the base and h is the height of the cone. This equation shows how the area of the circular base, multiplied by the height, is scaled down by one-third to account for the cone’s tapered shape.
Step-by-Step Calculation
To apply the formula, follow these steps:
- Measure the radius of the cone’s base.
- Find the height, which is the perpendicular distance from the base to the tip.
- Substitute these values into the formula.
- Multiply the radius squared by π, then multiply by the height.
- Finally, divide the result by three to get the capacity.
Example Calculation
Suppose we have a cone with a radius of 5 units and a height of 12 units. Using the formula:
| Step | Calculation | Result |
|---|---|---|
| 1 | Radius squared (5²) | 25 |
| 2 | Multiply by π (25 × π) | 78.54 |
| 3 | Multiply by height (78.54 × 12) | 942.48 |
| 4 | Divide by 3 (942.48 ÷ 3) | 314.16 |
Therefore, the interior capacity of the cone is approximately 314.16 cubic units.
Surface Area of Spheres Simplified
To calculate the outer measurement of a sphere, the goal is to determine the total extent of its curved exterior. Unlike shapes with flat sides, a sphere has no edges or vertices, so finding its total exterior involves a specific formula that accounts for its symmetrical shape. This process is essential when calculating how much material is needed to cover spherical objects, such as balls or tanks.
The formula for calculating the total exterior measurement of a sphere is:
4πr²,
where r is the radius of the sphere. This equation provides a straightforward method to determine the total surface, as it multiplies the radius squared by four times pi, reflecting the sphere’s symmetrical nature.
Understanding this formula allows for easy application in various practical situations, ensuring that calculations for spherical objects are both accurate and efficient. Whether you’re working on geometry problems or real-world design projects, knowing how to compute the outer measurement of a sphere is a vital skill.
Applying Formulas in Real-Life Scenarios
Understanding geometric formulas goes beyond the classroom; they are essential tools for solving everyday problems. From calculating how much paint is needed to cover a surface to determining the amount of water a container can hold, these formulas help make informed decisions in various fields. Applying these concepts to real-life situations allows for better resource management and design planning.
Here are some common real-life scenarios where these calculations are used:
- Packaging Design: Companies use geometric formulas to determine the size of boxes, containers, and other packaging materials. This ensures they use the minimum amount of material while maintaining the right capacity.
- Construction Projects: Builders rely on geometric measurements to calculate the amount of paint, wallpaper, or concrete needed for a specific area, ensuring accurate estimates and minimizing waste.
- Shipping and Storage: Understanding the interior capacity of various shapes (such as boxes or tanks) helps in optimizing storage space in warehouses or when loading items for transportation.
- Landscaping: Landscapers calculate the area of circular or other shaped garden beds to determine the quantity of soil, mulch, or plants needed to fill them.
- Sports Equipment: For items like basketballs, soccer balls, or golf balls, manufacturers calculate the external measurement to determine the amount of material required and ensure optimal performance.
By mastering the formulas for calculating size and external measurements, you can easily apply these concepts to solve practical problems, making your everyday tasks more efficient and precise.
Common Mistakes in Surface Area Calculations

When calculating the external measurements of geometric shapes, it’s easy to make errors that lead to incorrect results. These mistakes can occur at any stage of the process, from misinterpreting the formula to incorrect measurements or calculation steps. Identifying and understanding these common pitfalls can help avoid costly errors, especially when these calculations are used for practical purposes like construction or design.
Here are some common mistakes people make when performing external measurement calculations:
- Incorrectly Applying the Formula: One of the most frequent errors is using the wrong formula for the shape. It’s important to ensure that the formula matches the specific geometry being calculated, such as confusing a rectangular prism formula with that of a cylinder.
- Forgetting to Square the Radius: In calculations involving circular bases, it’s crucial to square the radius. A common mistake is to skip this step, leading to an underestimation of the total measurement.
- Overlooking Units of Measurement: Failing to maintain consistent units can result in incorrect results. Always make sure that all measurements (e.g., radius, height) are in the same unit before performing calculations.
- Misunderstanding Dimensions: Confusing the height or radius in three-dimensional shapes is another common mistake. For example, mixing up the radius and the diameter when calculating the external measurement of a sphere can lead to significantly incorrect answers.
- Omitting Certain Components: In shapes with multiple parts, such as cylinders, it’s easy to forget to include both the lateral and base components when summing up the total external measurement. Missing even one part of the shape can lead to an incomplete result.
By being aware of these common mistakes, you can ensure more accurate calculations and avoid potential setbacks in your projects.
Using Geometry to Solve Word Problems
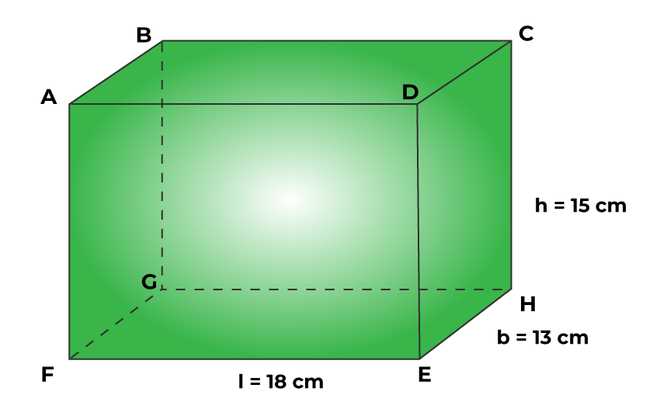
Geometry is a powerful tool for solving real-world word problems, as it allows us to translate complex scenarios into manageable mathematical equations. By applying geometric principles, we can break down the given information and find solutions to practical challenges, from calculating the amount of material needed for construction to determining the capacity of containers. Understanding how to recognize geometric relationships in everyday situations is crucial for effectively solving these types of problems.
Here are some common types of word problems where geometric principles can be applied:
- Determining the amount of paint required: If you need to cover a cylindrical tank with paint, you can use the formula for calculating the exterior to find how much paint will be needed for the job.
- Figuring out the amount of soil for a garden: For irregular garden shapes, you can use various geometric formulas to calculate the area and estimate how much soil, mulch, or fertilizer will be required.
- Estimating storage capacity: For items like water tanks or silos, you can apply geometric equations to determine how much liquid or material the container can hold, making it easier to plan for large-scale projects.
- Calculating material costs: In construction or manufacturing, you may need to calculate the amount of material required to cover a particular shape. Using formulas for exterior measurement and volume, you can easily determine how much material is necessary to meet specifications.
When faced with a word problem, the key is to identify the geometric shape or relationship being described and apply the appropriate formula. This approach makes it possible to find precise solutions to a wide variety of practical challenges.
Importance of Units in Volume Calculations
Units play a critical role in all types of measurements, particularly when calculating the capacity of objects or spaces. Without properly accounting for units, even the most accurate mathematical calculations can yield incorrect or meaningless results. It is essential to ensure that measurements are expressed in consistent units throughout the entire calculation process, as different units can represent vastly different quantities.
Here are some key reasons why units are so important when determining capacity:
- Accuracy in Results: Using the correct unit of measurement ensures that the final result is accurate and reflects the actual size or capacity of the object being measured. For example, confusing cubic meters with cubic centimeters would lead to vastly different results, even if the calculations are otherwise correct.
- Consistency Across Calculations: Consistent units across all steps of the calculation process are crucial to obtaining a valid result. Switching between different systems of measurement (such as metric and imperial) without conversion will lead to errors.
- Ease of Interpretation: Proper units make the results easier to understand and apply. For instance, if the final capacity is expressed in liters, it’s far more practical than if the same result were given in cubic inches or other less familiar units.
- Conversion Between Units: Knowing how to convert between different units is essential for working with data from various sources. For example, converting from meters to feet or from liters to gallons allows for more effective communication and comparison of measurements.
By paying close attention to units, you can ensure that your calculations are both accurate and relevant. Whether you are measuring physical objects, calculating material requirements, or estimating space usage, the correct units ensure that your results are meaningful and applicable in real-world contexts.
Volume vs Surface Area: Key Differences
Although both dimensions are essential in geometry, there is a distinct difference between measuring the internal capacity of a shape and calculating the extent of its outer boundaries. One focuses on the space an object occupies, while the other refers to the total extent of its outer face. These two concepts are often confused, but they serve different purposes in both practical and theoretical applications.
Here are the main distinctions between these two measurements:
- Purpose: The first measures how much space an object can hold, such as the amount of liquid a container can store. The second measures how much material would be needed to cover the object, such as the surface area of a ball or the exterior of a building.
- Formula: The formula for the first typically involves multiplying dimensions like length, width, and height, often resulting in cubic units. The formula for the second involves calculating the area of each face or curve of the object, often yielding square units.
- Units: For the first, the units are cubic (such as cubic meters or liters), as they represent three-dimensional space. For the second, the units are square (such as square feet or square centimeters), as they represent two-dimensional space.
- Applications: The first is useful for determining capacity, such as how much liquid or material can fit inside an object. The second is typically used for finding the amount of material required to cover an object or to calculate the external characteristics of a shape.
Understanding the differences between these two types of measurements is crucial in fields like architecture, engineering, and even everyday tasks like shopping for paint or calculating storage capacity. While they might seem similar at first glance, each provides valuable insights that help solve different kinds of problems.
Practice Problems with Solutions Provided
Engaging with practice exercises is one of the most effective ways to reinforce your understanding of geometric concepts. By solving problems that involve different shapes and their measurements, you can apply the theoretical knowledge to real-life situations. This section provides a series of practice questions along with their step-by-step solutions to help you better grasp the material.
Problem 1: Calculate the Capacity of a Rectangular Box
A box has a length of 8 cm, a width of 5 cm, and a height of 10 cm. Find its capacity.
Solution: To calculate the capacity, multiply the length, width, and height:
Capacity = 8 cm × 5 cm × 10 cm = 400 cm³
Problem 2: Find the Total Exterior Coverage of a Cylinder
A cylinder has a radius of 4 cm and a height of 12 cm. Determine the total external coverage.
Solution: First, calculate the area of the two circular bases and the lateral area. The formula for the total exterior coverage of a cylinder is:
Exterior Coverage = 2πr² + 2πrh
Substitute the values:
Exterior Coverage = 2π(4 cm)² + 2π(4 cm)(12 cm) = 2π(16 cm²) + 2π(48 cm) = 32π cm² + 96π cm = 128π cm²
So, the total external coverage is approximately 402.12 cm².
These problems will help reinforce the concepts of calculating internal capacity and external coverage, providing a foundation for tackling more complex problems. By following these solutions, you can build your skills and approach similar questions with confidence.
Visualizing 3D Shapes for Better Understanding
One of the most effective ways to enhance comprehension of geometric concepts is by visualizing three-dimensional objects. Understanding how different shapes occupy space and their relationships with each other allows for clearer problem-solving. When it comes to geometry, being able to mentally rotate, scale, or modify objects helps to build a strong foundation for complex calculations and real-world applications.
Understanding Geometric Properties Through Models

To fully grasp how three-dimensional objects behave, it is crucial to work with physical or digital models. By interacting with tangible or virtual representations of shapes, such as cubes, spheres, and pyramids, one can better understand their proportions, angles, and symmetries.
Tips for Effective Visualization
Here are a few tips to enhance your ability to visualize 3D shapes:
- Start simple: Begin with basic shapes and gradually increase complexity as you become more comfortable.
- Use software tools: There are many online tools available that allow for rotating and zooming into 3D models, which can improve spatial understanding.
- Sketch frequently: Drawing 3D shapes, even in basic form, can strengthen your ability to visualize them in more detail.
Practical Examples of 3D Visualizations
Let’s take a look at a simple example of how shapes are visualized using basic measurements:
| Shape | Key Properties | Visualization Tips |
|---|---|---|
| Cube | Equal edges, right angles | Visualize as stacked cubes or draw grids on the faces |
| Sphere | Constant radius, round shape | Think of it as a ball or globe |
| Cylinder | Circular bases, straight sides | Imagine a can or pipe |
By visualizing 3D objects, students and learners can deepen their understanding of geometric principles, making abstract concepts more tangible and easier to apply in various scenarios.
How to Use the Answer Key Effectively
Utilizing a solution guide can be an invaluable tool for improving your understanding of mathematical and geometric concepts. However, it’s essential to approach it strategically to get the most out of it. Simply looking at the solutions without engaging with the problem won’t help in the long term. Instead, active involvement with the guide is key to mastering the material.
Steps to Make the Most of the Solution Guide
- Attempt the problem first: Always try to solve the problem on your own before referring to the guide. This helps you identify areas where you need improvement and ensures you engage with the material.
- Understand the process: Don’t just look at the final result. Focus on the steps and logic used to arrive at the solution. This will help reinforce the methods involved.
- Work through examples: If you don’t understand a step in the solution, try doing a similar problem to see the process in action. This can help clarify any confusion.
- Review mistakes: If you made an error while solving a problem, take the time to review where you went wrong. Understanding your mistakes is crucial for improving your skills.
Why the Answer Guide Should Be a Learning Tool
Using a solution guide is not about just checking answers–it’s about deepening your understanding and reinforcing concepts. By carefully examining each step, you can develop a stronger grasp of the techniques involved, making it easier to apply them to similar problems in the future. Remember, the goal is to learn, not just to get the right answer.
When used thoughtfully, a solution guide can enhance problem-solving skills and boost your confidence, helping you to approach future challenges with a clearer perspective and greater preparedness.
Tips for Mastering Geometry in Chapter 10
Successfully understanding geometric concepts requires a blend of theoretical knowledge and practical application. As you work through the material, it’s important to focus not only on memorizing formulas but also on grasping the underlying principles. Developing a strong foundation in geometry will make problem-solving more intuitive and less daunting.
Here are a few strategies to help you master the material effectively:
- Understand the basics: Before diving into complex problems, ensure you have a solid grasp of the fundamental concepts. Familiarize yourself with shapes, their properties, and how to apply the appropriate formulas.
- Practice regularly: Geometry is best learned through consistent practice. Solve a variety of problems to build confidence and improve your ability to recognize patterns in different situations.
- Visualize the shapes: Try to visualize the geometric figures as 3D models or draw them out. This makes it easier to understand how formulas relate to real-world objects and scenarios.
- Break down complex problems: When faced with complicated questions, break them down into smaller, more manageable parts. Tackling each component one step at a time can make the process more understandable.
- Review mistakes: Don’t shy away from errors. Analyzing your mistakes is an excellent way to reinforce learning and avoid similar errors in the future.
By incorporating these strategies into your study routine, you’ll enhance both your understanding and your ability to apply geometric principles with confidence.
Summary of Volume and Surface Area Topics
This section provides an overview of the essential concepts related to calculating the capacity and outer measurements of various 3D shapes. Understanding these principles is crucial for solving real-world problems, from determining the amount of material needed to construct an object to calculating the space it occupies. The following key topics are covered in this area:
- Understanding 3D shapes: Different types of 3D objects, such as prisms, cylinders, cones, and spheres, each have unique properties that require specific formulas for measurement.
- Formulas for capacity: Determining how much space a 3D object holds involves specific mathematical expressions that relate to the shape’s dimensions, such as height, radius, and base area.
- Outer measurement calculations: The total outer extent of an object is determined by adding together the measurements of its sides, faces, or edges, depending on the shape. This is essential for determining the amount of material needed for construction or wrapping.
- Real-life applications: These concepts are not just theoretical; they apply to everyday situations such as designing packaging, determining the amount of paint needed for a surface, or calculating the volume of a storage tank.
- Common challenges: Students often struggle with distinguishing between formulas for different shapes or applying the correct units in calculations. Paying attention to details and practicing different scenarios helps overcome these challenges.
By reviewing these fundamental topics, you’ll gain a deeper understanding of how to approach problems involving the capacity and outer dimensions of various objects, both in theory and in practical applications.